О методе оценки распределения пластической деформации в области вершины усталостной трещины на основе решения задачи линейной теории упругости

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2023PNRPU MECHANICS BULLETIN

В рамках линейной механики разрушения в деформированной области вблизи трещины (за исключением малой окрестности у её вершины) компоненты поля напряжений могут быть представлены в виде асимптотических формул [1; 2]. Исходя из них, при приближении к вершине трещины напряжения неограниченно растут, а в точке, соответствующей вершине трещины, становятся равными «бесконечности». В действительности всегда в некоторой конечной области развиваются интенсивные пластические деформации, в результате которых перестаёт быть справедливым закон Гука и появляется нелинейная зависимость между напряжениями и деформациями. Описание напряжённо-деформированного состояния в области вершины усталостной трещины конечной длины требует учёта размера зоны пластической деформации. В условиях, когда прилагаемые нагрузки относительно невелики и в сечениях с трещиной не возникает больших пластических зон, соизмеримых с остаточным сечением детали, можно воспользоваться выражениями и критериями линейной механики разрушения, введя пластическую поправку Ирвина. Она заключается в замене реальной длины трещины на эффективную [3] и позволяет исключить из рассмотрения эффекты, возникающие от пластической зоны [4]. Другой вариант учёта пластических деформаций у вершины трещины был предложен Диксоном [5; 6]. Его подход позволяет оценить напряженно-деформированное состояние в области вершины трещины с учетом зоны пластической

В [7; 8] на основе гипотезы Диксона показано, что работа пластической деформации и, как следствие, диссипация тепла в вершине трещины может быть разделена на две части, соответствующие обратимой (циклической) и монотонной пластическим зонам. Этот вывод нашел экспериментальное подтверждение в работах [9– 11], где на основе энергетического подхода показана удовлетворительная корреляция между скоростью роста усталостной трещины и скоростью диссипации тепла в области ее вершины.

Реальные форма и размер зоны пластической деформации зависят от большого набора факторов, включающих свойства материала и условия нагружения [12–14]. Так, в работе [15] показано, что увеличение коэффициента Пуассона приводит к значительному уменьшению размеров пластической зоны, значительное сужение наблюдается вдоль направления оси трещины. Одним из результатов работы [16] является установление связи коэффициента асимметрии цикла с соотношением глубины монотонной и циклической пластических зон под поверхностью усталостных изломов при длине трещины, равной длине зоны стабильного роста трещины на поверхности усталостных изломов. Степень соответствия результатов аналитических расчётов с полями напряжений и деформаций определяется на основе прямых натурных или полунатурных экспериментов. Экспериментальные способы регистрации реального поля деформаций у вершины усталостной трещины начали свое развитие с методик на основе фотоупругих покрытий [17]. Современные технологии располагают оптическими камерами высокого разрешения, которые позволяют бесконтактно регистрировать изображения поверхности материала в процессе деформирования и с последующим применением метода корреляции цифровых изображений получать поля деформации в интересующей области [18; 19]. Метод также применялся для изучения процесса закрытия трещины [20–22], расчёта J-интеграла [23–25], расчёта коэффициента интенсивности напряжений [26– 28]. В работе [29] на основе метода корреляции цифровых изображений развита компьютерная система стереозрения, с помощью которой проведено исследование процесса роста усталостной трещины в металлических сплавах и количественно рассчитаны скорость роста усталостной трещины, максимальное значение деформации и эффективный коэффициент асимметрии цикла. Совместная оценка характеристик поврежденности, акустической эмиссии и локальной деформации на основе метода корреляции цифровых изображений в работе [30] показала, что увеличение сдвиговой компоненты при растяжении приводит к изменениям механических и акустических свойств, а также критической температуры хрупкости. В [31] для сплава Д16ч на основе метода корреляции цифровых изображений выявлено увеличение площади пластических зон в образцах после эксплуатации в условиях циклического нагружения.

Целью данного исследования является экспериментальное обоснование возможности аппроксимации напряженно-деформированного состояния в пластической зоне с помощью решения линейной упругой задачи о бесконечно тонком разрезе (гипотезы Диксона) на основе метода корреляции цифровых изображений, а также установление степени соответствия получаемых экспериментальных полей деформации модельным.

• 1.    Материалы и условия эксперимента

• 2.    Анализ экспериментальных данных и их сопоставление с результатами численного моделирования

В настоящей работе для регистрации поля деформации у вершины усталостной трещины использовался метод корреляции цифровых изображений. Запись изображений производилась оптической камерой Basler acA2440-75uc c объективом TC23007 OptoEngineering для достижения пространственного разрешения не менее 3 мкм. Частота записи данных составляла 100 Гц. Обработка полученных данных проводилась на основе программного обеспечения Lavision. Перед применением методов корреляции цифровых изображений для каждого кадра производилась корректировка по уровню дисторсии линзы, компенсация относительного движения образца и регулировка освещённости.

Плоские образцы с боковым концентратором напряжений, изготовленные из технического титана ВТ1-0 и титановых сплавов ОТ4-0 и ПТ-3В, в состоянии поставки подвергались циклическому деформированию с одновременной регистрацией поля деформации в области концентратора напряжений. Перед началом эксперимента поверхность образцов полировалась. Геометрия образцов представлена на рис. 1.

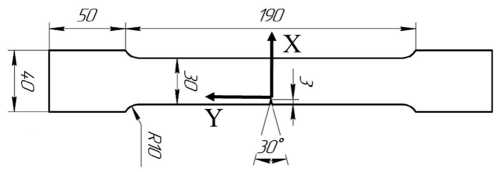
Рис. 1. Геометрия образцов (толщина листа технического титана ВТ1-0 и титанового сплава ПТ-3В – 3 мм, толщина листа титанового сплава ОТ4-0 – 4 мм, начало координат в вершине выреза)

Fig. 1. Samples geometry (thickness of Ti Grade 2 and Ti Grade 9 is 3 mm, thickness of Ti-1.1Al-0.9Mn is 4 mm, origin at the vertex of the notch)

Циклическое нагружение образцов производилось на серво гидравлической испытательной машине Bi-00-100 с постоянной максимальной нагрузкой в цикле 7,5 кН для технического титана ВТ1-0, 11кН – для титанового сплава ОТ4-0 и 8,5 кН – для титанового сплава ПТ-3В. Частота нагружения составляла 10 Гц, коэффициент асимметрии цикла – R =0,1. Длина трещины в ходе испытания измерялась методом падения электрического потенциала. Поле деформации в области вершины усталостной трещины регистрировалось при разных длинах трещины.

В основе подхода Диксона лежит гипотеза о связи между упругой и полной деформациями в вершине усталостной трещины с использованием модуля Юнга и секущего модуля упругости [5; 6]:

E

e f =1^1 s -J'                    (1)I Es J где 8 j - полная деформация, 8 j - упругая деформация для трещины аналогичной длинны при заданной нагрузке, Е - модуль упругости, Es = f (8) = ae / 8e - секущий модуль, зависящий от деформации и определяемый из диаграммы эффективных напряжений σe и деформаций εe [5] для соответствующей деформации. Для расчёта секущего модуля сделано допущение о равенстве эффективных характеристик и осевых.

° e = V ( ° * ° У )² ^ У —°- ' ) ^{2 +(a} - -° * ^{) 2 + 6} (^ ^+Т У ^+Т2= ) = ° У

⁸ e = "у ( ⁸ x ^{- 8} y ) 2 ⁺ ( ⁸ y ^{- 8} - ) 2 ⁺ ( ⁸ - ^{- 8} x ^{) 2 +} 2 ( Y ⁺ Y 2 - ⁺ Y 2 - ) = ⁸ y

Напряжение σ y и деформация ε y определяются из эксперимента по одноосному растяжению. Для каждой точки на диаграмме деформирования рассчитан секущий модуль. Диаграмма деформирования и секущий модуль упругости представлены на рис. 2, 3 соответственно.

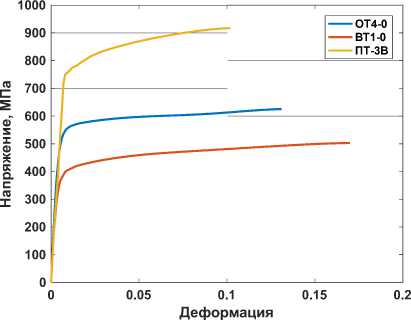
Рис. 2. Диаграмма деформирования

Fig. 2. Deformation diagram

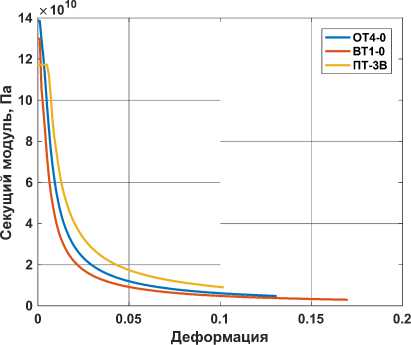
Рис. 3. Секущий модуль упругости

Fig. 3. Secant modulus of elasticity

Соотношение (1) введено как гипотеза в работах [5; 6] для связи экспериментально измеренной деформации и решения линейно-упругой задачи о бесконечно тонком разрезе в пластине.

Для определения процесса деформирования плоского образца с боковой трещиной различной длины решается задача линейной теории упругости для плоско напряженного состояния в пакете конечно-элементного моделирования Comsol Myltiphysics на основе системы уравнений:

V-n = 0

E v a =  -----—-------/i (8)g +

(1 + v)(1 - 2v) 1

• 8 = ^2 ^Vu + Vu T ]

где 8 - тензор деформаций, a - тензор напряжений, / 1 ( 8 ) - первый инвариант тензора деформации, u - вектор перемещений, g – единичный тензор, ν – коэффициент Пуассона.

При моделировании поведения образца при одноосном растяжении задавались следующие граничные условия: один торец жестко закреплен, на втором торце – усилие, соответствующее максимальному усилию в цикле, реализованному в лабораторных циклических испытаниях образцов. Трещина задавалась в виде треугольного выреза с радиусом кривизны 100 мкм. Расчетная область разбивалась на конечные элементы с уменьшением их размера от крупного (торцы образца) до минимального (область перед треугольным вырезом). Для определения допустимого минимального размера конечных элементов предварительно было проведено исследование на сеточную сходимость. Размер конечных элементов уменьшался до тех пор, пока изменение осевой деформации в районе выреза по сравнению с предыдущим шагом (размером элементов) превышало 5 %. Итоговый размер конечного элемента в области вершины трещины составил 22 мкм. При расчёте использовалась линейная аппроксимация поля перемещений на элементе. Полученное в результате численного решения поле компоненты вдоль оси образца тензора деформации (ε y ) пересчитывалось по формуле (2) в поле осевой компоненты тензора полных деформаций, которое сравнивалось с экспериментальными измерениями.

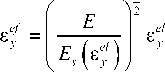
где 8 ^el - компонента деформации вдоль оси образца из решения упругой задачи, 8 ^ef - компонента полной деформации вдоль оси образца. Секущий модуль в формуле (2) определяется из диаграммы деформирования и зависит от деформации. При пересчёте деформации по формуле (2) используется секущий модуль, соответствующий деформации, для которой производится пересчёт. В данной работе секущий модуль рассчитан по результатам испытаний на одноосное растяжение. На рис. 4–6

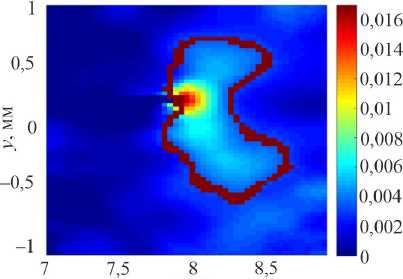
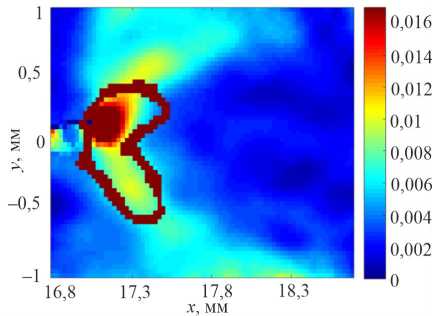
представлены характерные поля компоненты тензора деформации вдоль оси образца в области вершины трещины, полученные методом корреляции цифровых изображений в ходе усталостных испытаний образцов из технического титана ВТ1-0 и титановых сплавов ОТ4-0 и ПТ-3В и результаты вычислений. В распределении деформаций, полученных методом корреляции цифровых изображений, наблюдается отсутствие симметрии. Это, вероятно, вызвано неидеальностью условий нагружения (закрепление образца, соосность захватов), постобработкой данных с видеосистемы (коррекция дисторсии и угла съёмки, компенсация движения объекта как жёсткого целого), которые становятся заметны на измеряемом масштабе порядка 2 мм. Из диаграммы деформирования материалов определён предел пропорциональности, который соответствует деформации 0,34 % для ВТ1-0, 0,38 % для ОТ4-0 и 0,72 % для ПТ-3В. Эти значения деформации соответствуют границам, отделяющим пластическую деформацию от упругой в области вершины трещины. На рис. 4–6 выделена изолиния, разделяющая упругую и пластическую деформацию.

X, мм

а

b

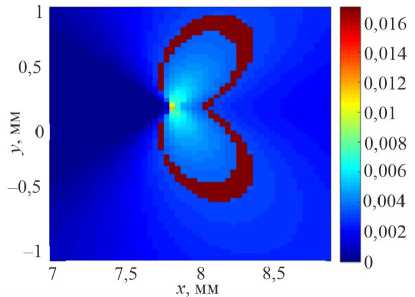
Рис. 4. Поле компоненты тензора деформации вдоль оси образца в области вершины трещины в титановом сплаве ОТ4-0, полученное методом корреляции цифровых изображений ( а ) и рассчитанное аналитически по формуле

Диксона ( b ) при длине трещины 7,5 мм

Fig. 4. Field component of the strain tensor along the specimen axis at fatigue crack tip of titanium alloy Ti-1.1Al-0.9Mn obtained by digital image correlation method ( a ) and calculation based on Dixon equation ( b ) with crack length 7.5 mm

b

1 0,016 0,014

' 0,012 0,01 0,008

■ 0,006

10,004

10,002

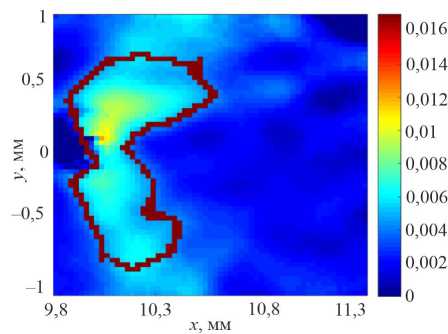
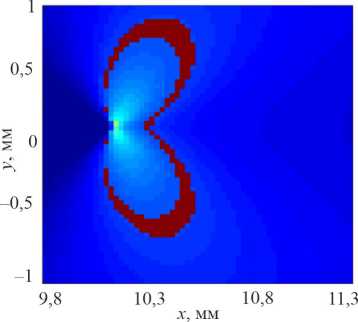
Рис. 5. Поле компоненты тензора деформации вдоль оси образца в области вершины трещины в титановом сплаве ВТ1-0, полученное методом корреляции цифровых изображений ( а ) и рассчитанное аналитически по формуле Диксона ( b ) при длине трещины 10 мм

Fig. 5. Field component of the strain tensor along the specimen axis at fatigue crack tip of titanium alloy Ti Grade 2 obtained by digital image correlation method ( a ) and calculation based on Dixon equation ( b ) with crack length 10 mm

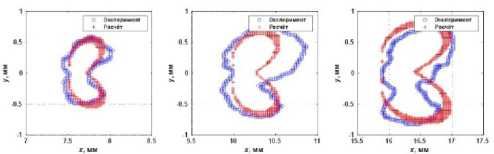
На рис. 7–9 представлено сравнение размера зоны пластической деформации в области вершины трещины, полученное в эксперименте и рассчитанное аналитически (ось ОХ направлена вдоль направления распространения трещины). Представлены результаты измерений для трёх величин длины трещины каждого материала.

В таблице представлены экспериментальные и аналитические значения размера зоны пластической деформации в области вершины трещины для исследуемых материалов. Под размером области пластической деформации понимается диаметр окружности, в которую вписывается изолиния деформации (выделена на рис. 4–6), соответствующая пределу пропорциональности.

b

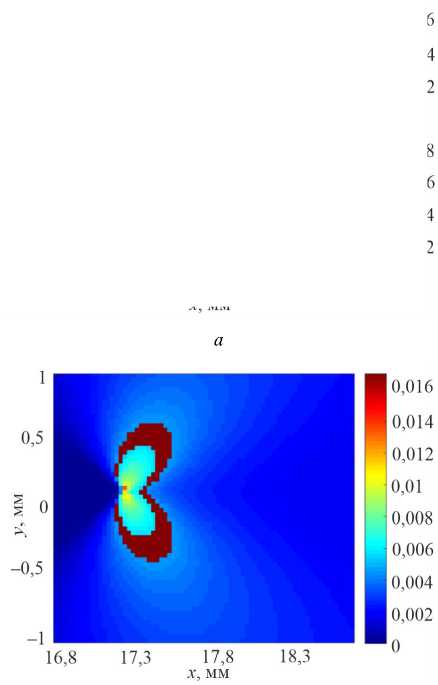
Рис. 6. Поле компоненты тензора деформации вдоль оси образца в области вершины трещины в титановом сплаве ПТ-3В, полученное методом корреляции цифровых изображений ( а ) и рассчитанное аналитически по формуле Диксона ( b ) при длине трещины 17 мм

Fig. 6. Field component of the strain tensor along the specimen axis at fatigue crack tip of titanium alloy Ti Grade 9 obtained by digital image correlation method (a) and calculation based on Dixon equation (b) with crack length 17 mm

а

b

c

Рис. 7. Характерный размер зоны пластических деформаций для длин трещины 7,5 мм (125е3 циклов) ( а ), 10 мм (131е3

полученных методом корреляции цифровых изображений даже при значительных длинах трещин для всех исследуемых материалов.

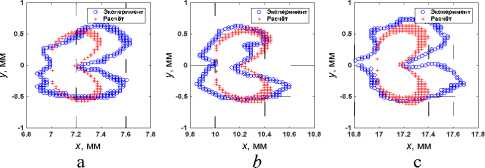
Рис. 8. Характерный размер зоны пластических деформаций для длин трещины 7 мм (89е3 циклов) ( а ), 12 мм (97е3 циклов) ( b ), 17 мм (100е3 циклов) ( c ) на образцах из титанового сплава ВТ1-0

Fig. 8. Characteristic size of plastic deformation zone with crack length 7 mm (89e3 cycles) ( a ), 12 mm (97e3 cycles) ( b ), 17 mm (100e3 cycles) ( c ) in sample of Ti Grade 2

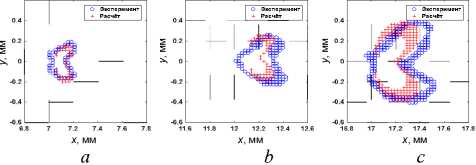
Рис. 9. Характерный размер зоны пластических деформаций для длин трещины 7 мм (95е3 циклов) ( а ), 10 мм (102е3 циклов) ( b ), 17 мм (107е3 циклов) ( c ) на образцах из титанового сплава ПТ-3В

Fig. 9. Characteristic size of plastic deformation zone with crack length 7 mm (95e3 cycles) ( a ), 10 mm (102e3 cycles) ( b ), 17 mm (107e3 cycles) ( c ) in sample of Ti Grade 9

Размер зоны пластической деформации в области вершины трещины

The size of plastic deformation zone at fatigue crack tip

Материал Длина трещина, мм Эксперимент, мм Численный расчёт, мм Ошибка, % ОТ4-0 7,5 1,1 1,16 5,45 ОТ4-0 10 1,52 1,44 5,26 ОТ4-0 15 1,76 1,7 3,41 ВТ1-0 7 1,22 1,15 5,74 ВТ1-0 10 1,27 1,2 5,51 ВТ1-0 17 1,33 1,28 3,76 ПТ-3В 7 0,38 0,37 2,63 ПТ-3В 12 0,51 0,49 3,92 ПТ-3В 17 0,83 0,78 6,02 циклов) (b), 15 мм (136е3 циклов) (c) на образцах из титанового сплава ОТ4-0

Fig. 7. Characteristic size of plastic deformation zone with crack length 7.5 mm (125e3 cycles) ( a ), 10 mm (131e3 cycles) ( b ), 15 mm (136e3 cycles) ( c ) in sample of Ti-1.1Al-0.9Mn

Получено качественно удовлетворительное соответствие оценки размера зоны пластической деформации на основе гипотезы Диксона и экспериментальных значений величины области пластических деформаций,

Заключение

В результате работы на основе метода корреляции цифровых изображений экспериментально получены поля деформации в области вершины усталостной трещины при различных значениях ее длины на образцах из технического титана ВТ1-0 и титановых сплавов ОТ4-0 и ПТ-3В с боковым надрезом. В конечно-элементном пакете Comsol Myltiphysics решена задача о деформировании плоских образцов с боковым надрезом в упругой постановке. Результаты численного моделирования полей деформаций при различных длинах трещины были скорректированы в соответствии с гипотезой Диксона о связи между реальными деформациями, упругим решением и величиной секущего модуля материала. Анализ результатов для трёх исследованных титановых сплавов показал качественно удовлетворительное соответствие между размерами зон пластических деформаций,