3D-модель «черного ящика» в задаче совмещения коники с квадрикой

Как правило при решении и исследовании задач геометрического моделирования стремятся получить геометрическую, часто 3D-реалистич-ную, или аналитическую модель. Однако для большинства прикладных инженерных задач характерна высокая сложность таких моделей, приводящая к множеству упрощений и допущений, либо невозможность или нецелесообразность их построения.

В экспериментальных исследованиях и задачах управления в таких случаях применяют модели «черного ящика», позволяющие исследовать объекты, внутреннее устройство которых неизвестно.

Цель работы - на примере задачи о совмещении коники с квадрикой показать 3D-метод компьютерного геометрического моделирования, не требующий построения явной геометрической или аналитической модели (модель «черного ящика»), а также рассмотреть решение указанной задачи.

Известны частные случаи задачи совмещения [1, 2 и др.] эллипса и конуса и их явные решения. Автор усложнил задачу, рассмотрев совмещение произвольной коники с произвольной квадрикой [3], а также ввел точку на поверхности квадрики, через которую должна проходить коника. В данной работе приведено решение для эллипса и однополостного эллиптического гиперболоида (ОГ).

Задача: даны эллипс и ОГ с наперед заданными параметрами. На поверхности ОГ задана точка. Определить положение эллипса, при котором он является сечением ОГ и проходит через заданную на нем точку («надеть» эллипс на ОГ).

Методика решения. Работа выполнялась в пакете AutoCAD, как наиболее адаптированном к теоретическим задачам геометрического моделирования [4].

Модель ОГ строим по характерным размерам (рис. 1), создав каркас из двух очерковых гипербол и 10^20 «поперечных» эллипсов и применив к нему команду Loft [5]. Гиперболы для каркаса получим как сечения эллиптического конуса [3].

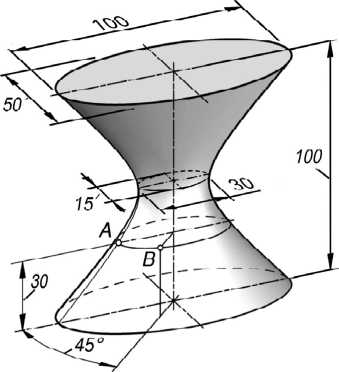
Рис. 1. Модель и параметры гиперболоида

Эллипс зададим двумя метриками dl и d* , где dl - длина большой оси, d* = d2 /dl - относительная длина малой оси d2 (рис. 2, a ). В процессе решения задачи эллипсы получались как сечения ОГ -сплайны. Для определения их метрик по методу хорд находим центр, затем с помощью дуги окружности, проведенной из центра и обрезанной контуром сплайна, находим ось и вершины, следовательно, dl и d2 .

Для повышения точности решения ОГ строили как линейчатую поверхность по трем направляющим. Добавив еще две направляющие, эллипс и его метрики находили по пяти точкам пересечения секущей плоскости с отрезками каркаса [5].

Все построения и вычисления выполнялись программными средствами AutoLISP [6]. Алгоритмы программной реализации, зачастую оригинальные, в данной работе не приводятся.

Частный случай задачи . Как правило в сложных моделях для их предварительной оценки первоначально выполняют упрощенные частные решения, которые получаются явными и геометрически точными. Для этого в рассматриваемой задаче рассмотрим совмещение заданных эллипса и ОГ без дополнительного ограничения в виде точки.

Эллипс ищем «просто» как фронтально-прое-цирующий, то есть перпендикулярный фронтальной плоскости симметрии ОГ. Пример на рис. 2 приведен для dl = 90; d* = 0.4. Впишем в ОГ сжатый эллипсоид, образованный вращением эллипса ef, подобного заданному эллипсу е (рис. 2, б ). Касание в двух точках приводит к распадению линии пересечения на два эллипса е' и е '' подобных заданному. Построение можно выполнить на проекционном чертеже (рис. 2, в ), где (2-3) - проекция эллипса е ' dl' - длина большой оси эллипса е ' или ef ; (4-5) - произвольная хорда, параллельная (2-3); 6 - ее средняя точка; отрезки (11-9) и (12-8) параллельны ( i -6) и проведены через точки 7, 10, е* и е** - найденные эллипсы, то есть решение задачи для ее частного случая.

По симметрии получим еще два фронтально-проецирующих эллипса е* ' е** ‘ (рис. 2, г ). Так же находим еще четыре профильно-проецирующих эллипса. Всего частный случай имеет восемь решений. В зависимости от параметров модели количество решений снижается до четырех или может отсутствовать.

Решение в частном случае задачи можно получить по 3D, если найти направление плоскости эллипсов е' или е '' поместить в нее искомый эллипс е и «лофтировать» его по фронтально-очерковой гиперболе h (рис. 2, д ). Пересечение полученного объекта с ОГ дает искомые эллипсы (рис. 2, е ).

Общее решение задачи. Были рассмотрены две точки: точка А , расположенная во фронтальной плоскости симметрии, и точка B общего положения (см. рис. 1). В каждом из вариантов не удалось получить явного геометрического или аналитического решения.

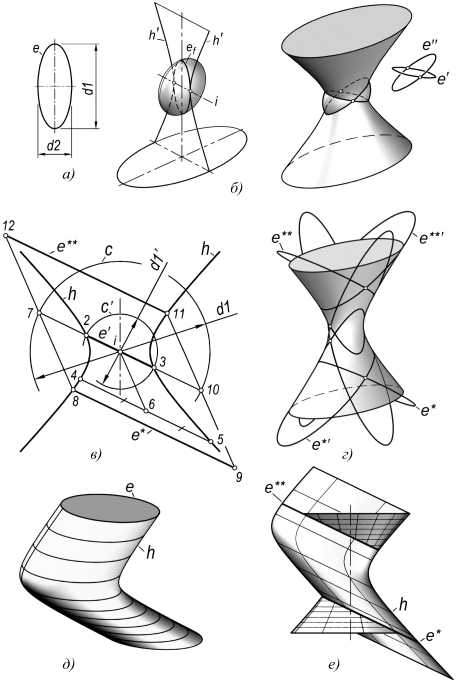
Рис. 2. Частный случай задачи: а - совмещаемый эллипс; б - сжатый эллипсоид при двойном соприкосновении с гиперболоидом; в - решение на проекционном чертеже; г - восемь решений для частного случая; д - вспомогательный объект; е - решение по 3D

Для решения по методу «черного ящика» построим множество возможных эллипсов, расположенных на поверхности ОГ и проходящих через заданную на нем точку. Из этого множества найдем эллипсы с требуемыми метриками.

Для создания множества

• 1)    введем секущую плоскость у (рис. 3), совершающую вращение вокруг двух осей, проходящих через заданную точку. Первое вращение вокруг оси il , параллельной оси i ОГ. Второе -вокруг горизонтали i2 , принадлежащей плоскости у и вращающейся вместе с ней вокруг il . Положение плоскости у зададим углом и между i2 и большой осью эллипса основания ОГ, а также углом w между плоскостью у и плоскостью основания ОГ;

• 2)    интервалы изменения и, w задаем такими, чтобы получить все множество коник. Для т. А , находящейся в плоскости симметрии, изменение и задаем в интервале (-90 ° , 0). Для точки B интервал изменения и (-90 ° , 90 ° );

• 3)    шаг вращений принимаем 0.5^1 ° . В этом случае размеры множеств составляют 20^40 тысяч. Они успешно обрабатываются на персональном компьютере;

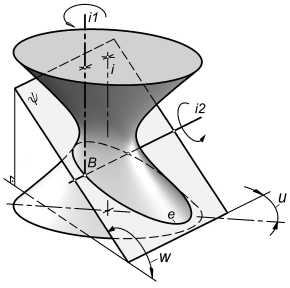
Рис. 3. Схема формирования множества коник для точки B

• 4)    для каждого сечения определяется тип коники, выбираются только эллипсы, находятся их метрики dl , d* и точки осей. Эти параметры, а также u,v -координаты секущей плоскости заносятся в базу данных (БД). Формирование БД происходит за 2^3 часа;

• 5)    далее по метрикам искомого эллипса в БД находим эллипс с близкими параметрами, извлекаем его uv -координаты и по ним строим сечение ОГ. Отклонение метрик построенного эллипса от заданных значений рассматриваем как погрешность решения;

• 6)    выделяя из БД подмножества с заданными характеристиками, строим различные зависимости, то есть исследуем модель. Все операции, а также построение графиков выполняются средствами AutoLisp.

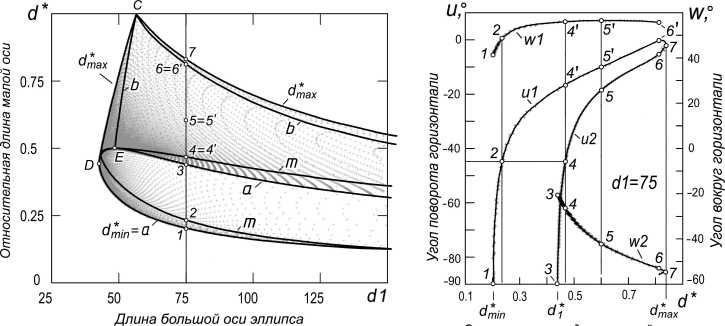
Решение для точки А . Отобразим БД, полученную для точки А и составляющую - 38 000 эллипсов, в координатах dl , d* (рис. 4, а ). Каждый эллипс отмечаем маркером точки. Получена область возможных решений.

Для исследования области определяем углы наклона эллипсов к плоскостям симметрии ОГ. Получаем зависимости, показывающие положение особых эллипсов. Так, кривые a - фронтально- проецирующие эллипсы, для них и = ±90°; кривые b - профильно-проецирующие, и = 0°; m - равно-наклоненные к плоскостям симметрии, и = ±45°,

Рассмотрим особые точки (см. рис. 4, а ). Точка С - два круговых сечения гиперболоида, проходящих через т. А . Точка D - фронтально-проеци-рующий эллипс с минимально-возможной длиной большой оси. Точка E - горизонтальный эллипс. Все особые эллипсы можно построить геометрически точно. Так для точки C достаточно построить круговые сечения ОГ на основе двойного соприкосновения со сферой и через точку А провести секущие плоскости, параллельные выявленным окружностям. Для точки D следует опустить перпендикуляр из точки A на противоположную ветку фронтально-очерковой гиперболы - это большая ось фронтально-проецирующего эллипса. Для точки E - построить горизонтальное сечение ОГ.

Исследуем количество возможных решений. Сделаем выборку (вертикальный «срез» области) мость угловых координат секущей плоскости от d* (рис. 4, б ). Получены две пары кривых. Первая пара ul(d*), w1(d*) , вторая - u2(d*) , w2(d*) . Каждая пара задает перемещение секущей плоскости, при котором образуются эллипсы с изменяемой длиной малой оси d* и постоянным значением большой оси dl = 75 .

Видим, что при d* <  d*_min решение отсутствует. В интервале d*_min< d* < d* имеется одно решение, определяемое парой ul, wl. В интервале d*_l< d* < d*_max добавляется решение от пары и2 , w2 , то есть имеется два решения. При d* > d*_max решение вновь отсутствует.

Количество решений указано для изменения u в интервале (-90 ° , 0). Полное количество решений вдвое больше. То есть область, ограниченная кривыми а (см. рис. 4, а ), соответствует двум решениям. Ее граничные точки 1, 3 - два совпадающих фронтально-проецирующих эллипса каждая, для них угол и = ± 90 ° (см. рис. 4, б ). Вне этой области возникает четыре решения.

Относительная Олина малой оси

а)                                               ^б)

Рис. 4. Исследование множества эллипсов, проходящих через точку А : а - область множества; б - угловые координаты секущей плоскости для dl = 75

Эллипсы в точках 2 и 4 являются равнонакло-ненными (принадлежат кривой m , угол и = ± 45 ° ). В точке 6 ‘ два симметричных профильно-проецирующих эллипса (принадлежат кривой b , и = 0). В точках 4\ 6, 7 - по два эллипса общего положения, причем в точке 7 эллипсы совпадающие.

В качестве примера построены эллипсы для точек 5, 5 ’ (рис. 5), соответствующих dl = 75, d* = 0.6. Получено четыре эллипса общего положения. Эллипсы el , e2 построены как сечения ОГ по координатам и , w секущей плоскости (см. рис. 4, б, точки 5, 5 ‘ ). Тот же результат получается при отыскании этих эллипсов непосредственно из БД по параметрам dl , d*. Еще два эллипса построены по симметрии: эллипс el ‘ симметричен el относительно фронтальной плоскости симметрии ОГ, эллипс е2' симметричен e2 .

Погрешность решения (см. таблицу на рис. 5) определяли как del =0.5 ( dell + del2 ), где dell , del2 -погрешности по метрикам dl , d* .

Решение для точки В . Область возможных решений (рис. 6) имеет значительно более сложный вид чем в примере с точкой А . Это отражает и более высокую сложность задачи, хотя с позиции рассматриваемого метода решения это не имеет значения: нужно построить множество эллипсов и делать по нему выборки.

В точках C ‘ , C возникают два различных круговых сечения ( 0 35.5 и 0 84.6). В точке Е образуется горизонтальный эллипс. Кривая a - фрон-тально-проецирующие эллипсы, кривые b , b\ b " -профильно-проецирующие эллипсы.

Рассмотрим срез области для эллипсов с длиной большой оси dl = 75 (см. рис. 6). Количество решений определяется (рис. 7, a ) количеством точек пересечения вертикальной линии с кривыми ul , и2 . Видим, что в интервалах d_min <  d* <  d*_l и d*₂< d* < d*_max существуют два решения. При d* <  d* <  d*₂ - от трех до пяти решений. При d* <  d*_min и d* >  d*_max решение отсутствует.

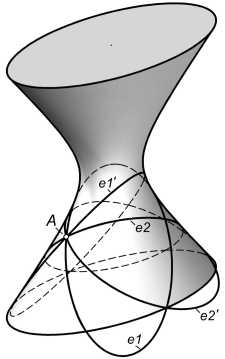
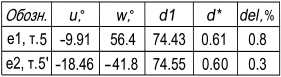
Рис. 5. Эллипсы через точку А для dl = 75 и d* = 0.6

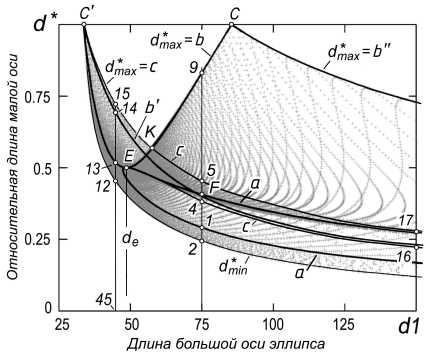
Рис. 6. Область множества эллипсов, проходящих через точку B

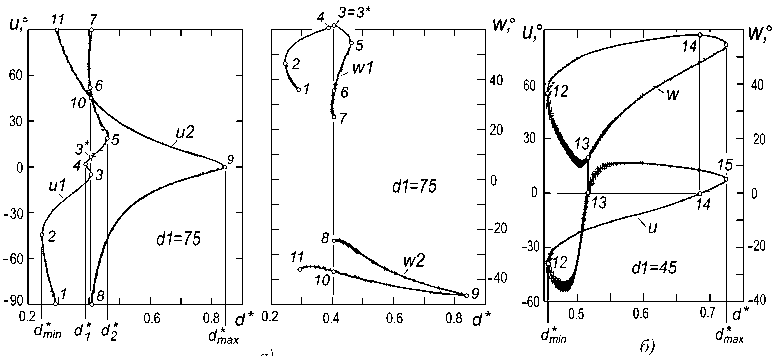
Рис. 7. Срез области определения для точки В : а - dl = 75; б - dl = 45

Эллипс	Точка	и,°	W, °	d1	d*	del, %
е1	8	-90	-25	75.4	0.43	2.6
е2	3	-3	62	75.8	0.4	1.8
-	3‘	4	62	76.5	0.39	3.5
еЗ	10	45	-37	75.5	0.41	0.3
-	6	47	36	75.6	0.4	1.6

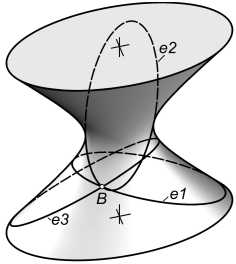
Рис. 8. Эллипсы через точку B для di = 75 и d* = 0.41 и оценка их погрешности

Построение множества подобных срезов для различных значений dl позволило выделить область (см. рис. 6), ограниченную кривыми с (16-4- E-K -5-17), в которой количество решений более двух. Эта область существует для dl >  de, (в нашем примере de ~ 48.51).

При dl <  de существуют по два решения в каждой точке области определения: вертикальная линия (рис. 7, б ) пересекает кривую и в двух точках.

Например, в точке F при dl = 75, d* = 41 (см. рис. 6) выявлено пять эллипсов, их u,v-координаты определены точками 8,3,3*,10,6 (см. рис. 7, а). Три из пяти эллипсов приведены на рис. 8. Эллипс el -фронтально-проецирующий (и = -90°, см. табл. на рис. 8); е2 - близок к профильно-проецирующему; е3 - равнонаклоненный к плоскостям симметрии ОГ (и = 45°).

Технологический пример. Рассмотрим квадрики как тонкостенные оболочки, которые следует сварить. Из технологических соображений сварной шов должен быть плоской кривой - эллипсом. Известно решение задачи в частном случае [1 и др.] для конуса и цилиндра. Наша методика позволяет «сварить» любые две квадрики, имеющие как сечение конику одного типа.

Пусть необходимо сварить эллиптический цилиндр, нормальное сечение которого задано как эллипс e * (рис. 9), и ОГ с заданными размерами. Оси цилиндра и ОГ параллельны. Сварной шов должен проходить через точку B на поверхности гиперболоида.

Решение заключается в извлечении из БД тех эллипсов, проекции которых на плоскости оснований цилиндра и ОГ имеют параметры эллипса е* (см. рис. 9).

Например, если для эллипса е* заданы метрики dl = 65, d* = 0.45, возникают три решения. Для двух из них построены модели подготовки оболочек под сварку (см. рис. 9).

О нахождении в БД эллипса с заданными метриками. База данных формируется как список на языке AutoLisp. Поиск ведется средствами обработки списков. Вводится допуск поиска del (см. выше). Первоначально, задав del = 5...7 %, находим множество из 30^100 эллипсов. Сортируем эти эллипсы по возрастанию угла и их плоскости и выделяем группы с близкими значениями и . Количество групп - это количество возможных решений. В каждой группе находим эллипс с минимальным значением del , которая является одним из решений. Чтобы «не потерять» решения, в слож-

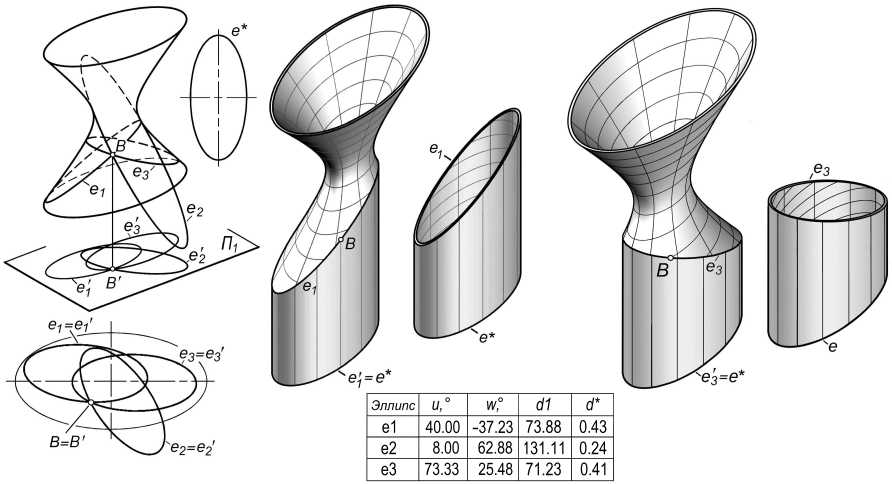
Рис. 9. Технологический пример: стыковка эллиптического цилиндра и гиперболоида

ных случаях строим зависимости (см. рис. 4, б и 7) и строим эллипсы по их uv -координатам.

Повышение точности решения до любого необходимого значения достигается созданием БД более высокой плотности или применением интерполяции.

Несмотря на то, что приведенные зависимости получены для фиксированных параметров ОГ и точек А , В , они являются характерными для рассмотренной задачи.

Другие варианты задачи совмещения коник и квадрик приведены в [3, 7].

Приведенное решение выполнено на персональном компьютере с параметрами, необходимыми для эффективной работы в пакете AutoCAD 2010. Затраты на формирование БД составляли 2^4 часа. Для работы с более сложными моделями возможны оптимизации программ и переход на более производительные, чем AutoLisp, языки программирования.

Выводы

• 1.    Сложный характер полученных в данной работе зависимостей позволяет с большой уверенностью утверждать, что геометрическая или аналитическая модели рассмотренной задачи вряд ли могут быть построены.

• 2.    Предложенный метод позволил найти решение и исследовать задачу с требуемой точностью.

• 3.    Рассмотренный метод в сочетании с 3D-алго-ритмами и программированием может быть рекомендован для практических задач геометрического моделирования, в которых построение аналитических и геометрических моделей затруднительно или неоправданно ввиду их сложности.