6-aperiodic words over the three-letter alphabet

Introduction. The paper is devoted to the study of sets of aperiodic words over a finite alphabet. The set of such words can be considered as some finite formal language.

The group B ( d , n ) with d generators and an identical relation x n = 1 is called a free Burnside group of rank d and period n.

The finiteness of a free Burnside group is established at different times for period two (the trivial case), for period three by W. Burnside, for period four by W. Burnside for two generating elements; by I. N. Sanov for an arbitrary number of generating elements, and for period six by M. Hall.

William Burnside one hundred and twenty years ago raised the question of local finiteness of groups, with the identity xⁿ = 1 [1]. This problem is known as the Burnside’s one. A group is called locally finite if any of its finitely generated subgroups is finite.

A negative answer to the Burnside problem was obtained in 1968 in the works of P. S. Novikov and S. I. Adyan [2–4]. The proof of the infinity of the group B ( d , n ), with the number of generators greater than or equal to two, for odd exponents exceeding 4380 was given in [2–4], and for odd periods exceeding 665 in S. I. Adyan monograph [5].

More detailed results on the Burnside problem can be found in the work of S. I. Adyan [6].

Theorems about non-repetitive words in a three-letter alphabet and 3-aperiodic words of any length in a two-letter alphabet were proved by A. Thue in 1906 [7] (see also lemma 1 in [6]). In the article by S. E. Arshon in 1937 [8], the existence of an n -digit asymmetric non-repetitive sequence for an alphabet of at least three letters is proved. In the monograph of S. I. Adyan [5] on pages 13–16, by means of Arshon's method [8] it was proved that there are infinite 3-aperiodic sequences in an alphabet of two characters. The work [9] belongs to the same theory. In the monograph of A. Yu. Olshansky [9] proved the infinity of the set of 6-aperiodic words in the two-letter alphabet and obtained an estimate of the number of such words of any given length.

A report on the topic of aperiodic words was made by the author at the conference “Reshetnev Readings” [10], then research on this issue was continued: in [11] A. Yu. Olshansky's assessment of the number of 6-aperiodic words in the two-letter alphabet was improved.

In this article, we study the set of 6-aperiodic words in the three-letter alphabet. The results obtained can be useful for encoding information in space communication sessions. Previously we also considered 5-periodic words [12] and 12-aperiodic words [13].

Main result. For ease of reading, we first give a few necessary definitions.

Definition. A periodic word with period H is any subword of some word Н^р , р > 0.

For example, ababa is a periodic word with the period ab or ba.

Definition. An l-aperiodic word is a word X that does not contain non-trivial subwords of type Y^l.

• S.    I. Adyan [4] proved that in the two-letter alphabet there is an infinite set of arbitrarily long 3-aperiodic words.

We also considered the problem of the existence of arbitrarily long words, free of squares, over the three-letter alphabet [8].

A. Yu. Olshansky [9] considered a set of 6-aperiodic words and obtained an estimate of the function f ( n ) of the number of such words of length n : there are arbitrarily long 6-aperiodic words and the number f ( n ) of such words of length n is greater than (³₂) ⁿ in the two-letter alphabet. A. Yu. Olshansky [11] improved this estimate of the number of 6-aperiodic words over the two-letter alphabet.

We are interested in estimating the number of 6-aperiodic words in the three-letter alphabet.

When getting the estimate, we apply the same method as A. Yu. Olshansky used [9].

Theorem. There are arbitrarily long 6-aperiodic words and the number f ( n ) of such words of length n is greater than (⁵₂) ⁿ in the three-letter alphabet.

Theorem proving. Let { a , b , c } be the alphabet. In this alphabet, we will consider 6-aperiodic words. First, we prove the inequality f ( n + 1) >  (5/2) f ( n ) using the method of mathematical induction.

Consider the case n = 1: f (2) >  52 ■ f (1), where f (1) = 3, f (2) = 9. It means that the base of induction is proved.

A 6-aperiodic word of length n + 1 can be obtained by adding the letters a, b, or c to the right of the 6-aperiodic word of length n . In this way 3 f ( n ) words X of length n + 1 are obtained.

Some of these words may contain A ⁶ degrees. Then estimate the number of such extra options.

When attributed to the right, the only identity of X = YA ⁶ form is obtained, since otherwise the beginning of the length n of the word X with the length n + 1 contains A ⁶ . For the words A of length 1 (only three such words), there are less than 3 f ( n - 5) words of X ^ YA ⁶ form, where the word Y is 6-aperiodic and Y = n - 5 :

(........ aa ... a ) a ,

1—',' n-55

(........ bb ... b ) b ,

V 1-----v-----' 1------V------1 7’ n-55

(........ cc ...c) c .

v ’—v—1 '—v—1 7 n-55

Obviously, there are 9 words A of length 2. The corresponding words of the X = YA ⁶ type of length n + 1 are less than 9 f ( n - 11), where the word Y is 6-aperiodic of length n - 11.

Continuing the reasoning in the same way, we have: f ( n + 1) >  3 f ( n ) - 3 f ( n - 5) -- 3² f ( n - 11) - 3 3 f ( n - 17) - ...

Since by the inductive assumption f (n) > (52)k ■ f (n - k), so f (n +1) > 3 f (n) - (3(52)-5 f (n) +

+ 3²(52) ^{- 11} f ( n ) + 3³(52) ^{- 17} f ( n ) + ...).

Transform the resulting inequality:

f ( n + 1) >  f ( n )(3 - (3(52) ^{- 5} + з² (52) ^{- 11} + 3 3 (52) ^{- 17} + ...).

Since 6/3 <  52 , so the geometric progression on the right side of the inequality is decreasing with the ratio 3(52) ^{- 6}.

Then estimate the second factor of the right part S using the geometric progression formula

S = 3 -

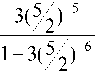
We need to prove that S >  52.

Transform this inequality:

³ - ⁹(⁵2     - ^3|52)' + 3(52) - ⁵ - 52 >  0

1 - 3(5/) - 6

After simplification we get:

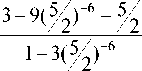
> 0.

Since 1 - 3(52) ⁶ >  0 , it remains to check the correctness of the inequality:

3 - ⁹(⁵2) ^{- 6} - % >  0.

We are convinced of its correctness by direct calculation. Hence, it is proved that the inequality f ( n + 1) >  52 f ( n ) exists for any natural n . The theorem is proved.

Conclusion. The problem of estimating the number of aperiodic words is still being studied. The set of 6–aperiodic words in the three-letter alphabet is considered and an estimate is obtained for the function of the number of such words of any given length.

Acknowledgment. This work is supported by the Krasnoyarsk Mathematical Center and financed by the Ministry of Science and Higher Education of the Russian Federation in the framework of the establishment and development of regional Centers for Mathematics Research and Education (Agreement No. 075-02-20201534/1).