6-апериодические слова над трехбуквенным алфавитом

Введение. Работа посвящена изучению множеств апериодических слов над конечным алфавитом. Множество таких слов можно рассматривать как некоторый конечный формальный язык.

Группа B ( d , n ) с d порождающими и тождественным соотношением xⁿ = 1 называется свободной бернсайдовской группой ранга d и периода n .

Конечность свободной бернсайдовской группы установлена в разное время для периода два (тривиальный случай), для периода три У. Бернсайдом, для периода четыре У. Бернсайдом для двух порождающих; И.Н. Сановым для произвольного числа порождающих элементов, для периода шесть М. Холлом.

Уильям Бернсайд сто двадцать лет назад поставил вопрос о локальной конечности групп, с тождеством xⁿ = 1 [1]. Сейчас этот вопрос известен как проблема Бернсайда. Группа называется локально конечной, если любая ее конечнопорожденная подгруппа конечна.

Отрицательный ответ на проблему Бернсайда был получен в 1968 г. в работах П.С. Новикова – С.И. Адяна [2–4]. Доказательство бесконечности группы B ( d,n ), с числом порождающих больше либо равным двух, для нечетных показателей, превышающих 4380 было дано в [2–4], а для нечетных периодов, превышающих 665 – в монографии С.И. Адяна [5].

Более подробно с результатами по проблеме Бернсайда можно познакомиться по работе С. И. Адяна [6].

Теоремы о бесповторных словах в алфавите из трёх букв и 3-апериодических слов любой длины в алфавите из двух букв доказал А. Туэ в 1906 г. [7] (см. также лемму 1 из [6]). В статье С.Е. Аршона 1937 г. [8] доказано существование n -значной ассиметричной бесповторной последовательности для алфавита не менее, чем из трех букв. В монографии С.И. Адяна [5] на с. 13–16 способом Аршона [8] доказано, что в алфавите из двух символов существуют бесконечные 3-апериодические последовательности. К этому же направлению относится работа [9]. В монографии А.Ю. Ольшанского [9] доказана бесконечность множества 6-апериодических слов в двухбуквенном алфавите и получена оценка количества таких слов любой данной длины.

Мной был сделан доклад по теме апериодических слов на конференции «Решетневские чтения» [10], затем исследования по этому вопросу были продолжены: в [11] была улучшена оценка А.Ю. Ольшанского из [9] количества 6-апериодических слов в двухбуквенном алфавите.

В данной статье будет изучено множество 6-апериодических слов в трехбуквенном алфавите. Полученные результаты могут быть полезны при кодировании информации в сеансах космосвязи. Мной также рассматривались ранее 5-периодические слова [12] и 12-апериодические слова [13].

Основной результат. Для удобства чтения приведем сначала несколько необходимых определений.

Определение. Периодическим словом с периодом Н называется любое подслово некоторого слова Н р , р>0.

Например, ababa - периодическое слово с периодом ab или ba.

Определение. l-апериодическим словом называется слово  Х,  не содержащее нетривиальных подслов типа Yl.

С.И. Адяном [4] доказано, что в алфавите из двух букв существует бесконечное множество сколь угодно длинных 3-апериодических слов.

Рассматривалась также задача о существовании сколь угодно длинных слов, свободных от квадратов, над алфавитом из трех букв [8].

А.Ю. Ольшанский в работе [9] рассматривал множество 6-апериодических слов и получил оценку функции f ( n ) - количества таких слов длины n : в двухбуквенном алфавите существует сколь угодно длинные 6-апериодические слова и число f ( n ) таких слов длины n больше, чем (^) ⁿ . В работе [11] автором улучшена эта оценка количества 6-апериодических слов над двухбуквенным алфавитом.

Для нас представляет интерес оценить количество 6-апериодических слов в алфавите из трех букв.

При получении оценки мы будем использовать метод, используемый А.Ю. Ольшанским в [9].

Теорема. В трехбуквенном алфавите существует сколь угодно длинные  6 - апериодические слова и число f (n) таких слов длины n больше, чем (^)n.

Доказательство . Пусть { a,b,c } - алфавит. В этом алфавите будем рассматривать 6-апериодические слова. Сначала докажем неравенство f ( n + 1) >  (5/2) f ( n ) при помощи метода математической индукции.

Рассмотрим случай n =1: f (2) > ^ • f (1), где f (1) = 3, f (2) = 9. То есть база индукции доказана.

6 -апериодическое слово длины n + 1 можно получить добавлением справа букв a, b или c к 6-апериодическому слову длины n . Таким способом получается 3 f ( n ) слов X длины n + 1 .

Часть из таких слов могут содержать степени A ⁶ . Оценим количество таких лишних вариантов.

При приписывании справа получится лишь тождество вида X = YA ⁶ , поскольку в противном случае начало длины n слова X длины n + 1 содержит A ⁶ . Для слов A длины 1 (всего три таких слова) имеется меньше, чем 3 f ( n — 5) слов вида X = YA ⁶ , где слово Y 6 -апериодично и | Y = n — 5 :

(........ bb...b) b, n-5      5

(........ cc ...c ) c.

n - 5       5

Очевидно, имеется 9 слов A длины 2. Соответствующих слов вида X = YA ⁶ длины n + 1 меньше, чем 9 f ( n - 11) , где слово Y 6 -апериодично длины n - 11 .

Продолжая рассуждения таким же образом, имеем:

f ( n + 1) >  3 f ( n ) - 3 f ( n - 5) - 3 2 f ( n - 11) - 3 3 f ( n - 17) - ...

Так как по индуктивному предположению f (n) > (52)k • f (n - k) , то f (n +1) > 3 f (n) -(3(52)-5 f (n) + 32(52Г" f (n) + ’-V 2|' f (n) +...).

Преобразуем полученное неравенство:

.f ( n + 1) >  f ( n )(3 - (3(52) ^{- 5} + 3²(5/)- ‘ ¹

+ 3 3 (52) ^{- 17}

+ ...) .

Поскольку -6/ 3 <

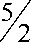
то геометрическая прогрессия в правой части неравенства является

убывающей со знаменателем 3(5^) ⁶ .

Оценим второй сомножитель правой части

S при помощи формулы геометрической

прогрессии

5 = 3 -

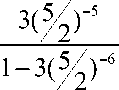
Нам нужно доказать, что 5 >

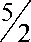
Преобразуем данное неравенство:

3 - 9(52) - ⁶ - -ч ⁵2)   + 3(5-2) - ⁵ - 52

1 - Х^)-^{6          >}

После упрощения получаем:

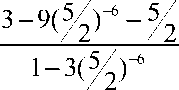
> 0.

Так как 1 - 3(52) 6 >  0 , то остается проверить верность неравенства:

3 - 9(52) ^- 6 - 52 >  0 .

Убеждаемся в его справедливости непосредственным вычислением. доказано, что неравенство f ( n + 1) > 5^ f ( n ) выполняется для любых

Следовательно, натуральных n .

Теорема доказана.

Заключение. Продолжается изучение вопроса об оценке количества апериодических слов. Рассмотрено множество шесть-апериодических слов в трехбуквенном алфавите и получена оценка для функции количества таких слов любой данной длины.

Acknowledgment. This work is supported by the Krasnoyarsk Mathematical Center and financed by the Ministry of Science and Higher Education of the Russian Federation in the framework of the establishment and development of regional Centers for Mathematics Research and Education (Agreement No. 075-02-2020-1534/1).