A 3-D Geometry based Remote Login 2-Way Authentication Scheme using Smart Card

Published Online July 2015 in MECS

Smart card based password authentication is one of the most convenient and commonly used two factor authentication mechanisms. This mechanism has been employed in several applications ranging from remote host login, online banking access control of restricted vaults, activation of security devices, etc. Due to distributed nature of the computer systems in a network spread over a large geographical area, the privacy of a user may lead to multifold vulnerability. In such environment, the login authentication is used to check the validity of a login request made by a remote user to gain access right on an authentication server.

There are various types of methods that can help in password authentication. Some are meant for a single system environment and some have been extended to multiserver environment. Since the computer systems are spread over various locations including multi-cities, the user privacy goes down and maintaining the user privacy including the security becomes a vital issue. The remote login methods help checking the login request sent by a remotely situated user to gain access right into an authentication server (AS). The password is shared by both the remote user as well as the authentication server to check the validity of that user. This method however has the security problem and requires overheads to maintain a table for containing the user identities along with passwords. The first scheme, whish is discussed by Lamport [1] for authentication system, uses a table that maintains passwords to check the authenticity of a user. This method however does not provide proper security because it stores the password table for authentication and the table may be manipulated or stolen. The newer techniques do not maintain the password tables.

Chang and Wu [2] have discussed a scheme that is based on simple Euclidean geometry. It provides no facility for changing the password, a necessary feature of a security system, and also suffers from various security vulnerabilities. The paper [3] discusses a method, which is based on the identity-based cryptosystems and signature schemes [4]. It overcomes the problems of conventional password authentication schemes. Wu discusses a remote login authentication method, which uses a smart card, to prevent the replay attack and impersonation attack [5]. This scheme employs simple arithmetic operations unlike the heavy exponential operations as used in the scheme discussed in [3]. The paper [6] discusses a scheme that prevents the replay attack by considering a timestamp in login phase. In this scheme, the computer system stores only a secret key, not the original password, to compute the user’s password on the basis on the submitted parameters by the user in the authentication phase. Computing the secret key from the known information is extremely difficult because of the discrete algorithm over a finite field. This scheme is however breakable because a legal user can masquerade as another legitimate user by making valid pairs of user identity without having any knowledge of the system security key. The methods based on the smart card are quite secure in authenticating a legitimate user. These types of methods are very commonly used in various applications such as banking, remote login, etc. Since our method is based on the smart card, it is not out of context to briefly discuss about the smart cards.

• A. Smart Card

A smart card is basically a plastic card of the same size as of a credit card. It has an embedded microchip, which is capable of storing the data, and it can be used in several applications; some of the common applications are given below:

• •    Dial a connection on a mobile telephone and be charged on a per-call basis.

• •    Establish your identity when logging onto an Internet access provider or to an online bank.

• •    Pay for parking at parking meters or to get on subways, trains, or buses.

• •    Provide hospitals or doctors your personal data without filling out a form.

A smart card generally contains more information than a magnetic stripe card, which can be programmed for different applications. Some of them are equipped with programmes and data that can support multiple applications and some may be updated to add new applications when they are issued. The smart cards are designed to be inserted into a slot and read by a special reader or to be read remotely, such as at a toll booth. They can be disposable such as at a trade-show or reloadable for most applications. The industry standard interface between programming and PC hardware in a smart card has been defined by the PC/SC Working Group that comprises of Microsoft, IBM, Bull, Schlumberger, and other interested companies. The most commonly used operating systems in smart cards are JavaCard and MULTOS. There are already more than a billion smart cards in use and the Europe ranks at the top. According to a market research report World Smart Card- Advanced Technologies, Application and Global Forecast (2008 – 2015), “the smart card market is expected globally to be worth US$6.6 billion by 2015, in which the telecom will account major part, nearly 53.8% of the total revenues.” According to the Smart Card Alliance , ‘There were approximately 120 million chip cards in the U.S. market by the end of 2014 and, at the end of 2015, 600 million are estimated.’ The Eurosmart provides a market study annually on global shipments of the smart cards, which reports, “over 8.790 billion devices will ship in 2015”

After discussing about the smart card market, we discuss important authentication schemes, which use the smart cards. Awasthi and Lal [7] discuss a method for remotely authenticating a user with the help of a smart card. It secures the previously generated password in the system even in case the security key of the system is compromised. Yoon et al. [8] discuss a new scheme based on the Chien et al.’s scheme [9] that enables a user to change his password at his will, without compromising the security, and no help from the remote system/server. In this method, a user is authenticated to the server and the server is authenticated to the user. The drawback of this scheme is heavy computational cost. In [10], Yang and Sheih report the weakness of the Wang and Chang’s scheme [11] and discuss two methods for password authentication using the smart card. One uses the timestamp and other is nonce-based method. In these methods, there is no need to maintain password or verification tables by the system for user authentication. Also, a user can change his password freely.

The paper [12] reports that the timestamp based method [10] is not resistant to the forgery attack. In [13], it is reported that the attack by [12] is unreasonable. It however discovers that the method in [10] is vulnerable to the forgery attack. The paper [14] improves the methods discussed in [10]. Lin et al. discuss Optimal Strong-Password Authentication (OSPA) protocol by overcoming the weaknesses of the SAS protocol [15]. Chen and Ku [16] show that both the SAS and OSPA protocols are prone to the stolen-verifier attack. Fan et al. [17] discuss a scheme that is able to foil the offline dictionary attack even in the case when the secret information in the smart card becomes known. Pathan and Hong [18] cryptoanlyze the scheme discussed in [14] and report that it is not secure against the various forgery attacks. In [19], it is reported that the Yang et al.'s improvements [14] yet cannot withstand the forgery attacks. Kumar [20] discusses a scheme in which the server and a user authenticate each other and communicate securely by using a generated secret session key. This scheme also provides freedom to a user to choose his password without connecting to the server. Kumar [21] discusses an authentication method using a smart card that provides two way mutual authentication between a user and the server. It also maintains the message confidentiality by using a common session key. The paper [22] discusses a remote password authentication scheme that can detect the wrong password in login phase. Furthermore, it is user-friendly and more secure. In [23], the biometric characteristics have been used for the server-side encryption and digital signature in which an end-user does not require any additional dongles, chips, tokens, cards, etc. The paper [24] discusses the graphical passwords for remote user authentication, which have better security and usability over the textual passwords. The paper [25] discusses a method for designing resilient and secure biometric features. It forms an ECG-hash code by taking the scalar product of the electrocardiogram (ECG) feature matrices of two remotely placed persons. This feature is unique and cannot be compromised in any circumstance unlike other features such as fingerprints, face recognition, etc. The paper [26] discusses biometric passports to prevent illegal entry by a person in a country. It consists of an IC chip in which the biometric characteristics are embedded and that chip is incorporated in the passport. The above reviewed methods use the smart cards; however, they do not talk about 3-D geometry, which can certainly increase the security aspects.

In this paper, we discuss a new method based on 3-D geometry instead of 2-D that can increase the system security and also has a feature of password change. Sometimes, it may happen that the adversary steals the smart card and using reverse engineering extracts the information stored in it. We have reviewed the remote authentication protocols as well the remote authentication schemes. The basic difference between a password authentication protocol and a password authentication scheme is that the former tries to prevent an unauthorized person to get any important information related to the password from the protocol transcript, assuming that the communicating parties are not compromised. On the other hand, the latter uses smart card for authentication. It is also required in a password authentication scheme that even if the smart card is compromised, the user password should not be insecure. Here, we discuss security requirements based password authentication scheme and also a generic construction framework with smart card using 3-D Euclidean geometry. The security requirement is different from the already existing ones. We show that our method more secure than the previously discussed methods. It also entails minimum computational cost and removes the pitfalls of the above mentioned schemes. The security analysis of our method is also discussed in the paper.

• II.    Proposed Work

Our proposed scheme is based on the 3-D Euclidean geometry and it uses the smart card. Like most of the password authentication schemes, it has four phases: initialization phase, registration phase, login phase, and authentication phase . It also provides a facility for changing the password to a legitimate user. When a user wishes to login to the system, he needs to insert his smart card into the device attached to the system and types in his identity and password. There are some necessary public parameters in the smart card besides the user identity, which are used in different phases. Normally, in real world applications, a password has a series of alphanumeric and other special characters. For simplicity, we assume in our scheme that the password consists of integer value only. We now discuss various activities done to carry out the authentication process. In these types of schemes, it is assumed that there is a central authority (CA).

• A.    Initialization

First of all initialization is done in which the central authority (CA) chooses a Galois field, denoted as GF(P), where P, f, and g refer to a large prime number, a oneway function, and a generator of the field GF(P), respectively. It also selects a secret key s, which is of minimum length 160 bits in order to prevent the brute force attack, and two pairs of secret keys: (x0, y0, z0), (x1, y1, z1). The one-way function simply means that, for a given value of X, it can easily compute the value of Y, (Y=f(X)), but to compute the value of X for a given Y, it is extremely difficult. The function f must be a symmetric enciphering algorithm such as data encryption standard (DES). The parameters P, f, and g are considered as public key and the pair of secret keys: (x0, y0, z0), (x1, y1, z1) are considered as private key. All the calculations in our scheme are performed over GF(P). This is the initialization phase that needs be performed beforehand, but only once. After that, other phases are performed. We now discuss registration, login, user authentication processes, followed by password change facility.

• B.    Registration Phase

In this phase, a new user who wishes to use the system/server’s services first registers with the system to become a legitimate user. This is a one-time process for every new user. The user chooses his password, not the user identity. The user id is supported by the system. The reason is that it is quite possible that a new user chooses his id which is already being used by some other user. We now discuss this registration process.

Suppose a new user U i wants to register with the system. He first chooses his own password, say, PWD i and provides f(PWD i ) to the central authority (CA). The user does not provide his actual password to CA. The following are the operations performed in this phase:

• a.    CA assigns an identity IDT_i to user U_i.

• b.    CA computes the following points:

A = (0, f(PWD i ), 0)

B = (f(IDT i .x 0 ), f(IDT i .y 0 ), f(IDT i .z 0 ))

C = (f(IDT i .x 1 ), f(IDT i .y 1 ), f(IDT i .z 1 ))

• c.    Construct a triangle (Δ) using A, B, and C points and calculate the centroid G = (G i1 , G i2, G i3 ) of the triangle ABC as follows:

G i1 = ((0 + f(IDT i .x 0 ) + f(IDT i .x 1 ))/3

G i2 = (f(PWD i ) + f(IDT i .y 0 ) + f(IDT i .y 1 ))/3

G i3 = (0 + f(IDT i .z 0 ) + f(IDT i .z 1 ))/3

• d.    Construct the line L_i using A and G.

• e.    Calculate the midpoint, A_1, of the line segment joining the points A and B.

• _{f.    Compute M = g}f(IDTi XOR s )+f(PWDi)

• g.    Store {IDT i , f, P, G, A 1 , M} in a smart card and send it to the user through a secure channel.

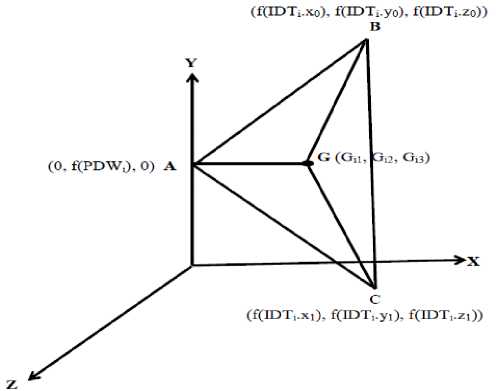
Fig.1. Graphical representation of Registration phase

In this phase, the CA does not have any knowledge about the user password. Fig.1 shows graphical representation of the registration phase for the user U i .

• C.    Login Phase

A registered user is allowed to login to the system. If some unregistered user tries to login to the system, he must be rejected by the system. For login process, the user submits his user identity and password to the system along with his smart card. He must insert his smart card into a terminal attached with the system. He must authenticate the server’s legitimacy before sending his details in order to login to the system. Following are the steps performed for authenticating the server.

• i.    Server Authentication Phase

• •    Server calculates M’’ = g^{f(IDTi XOR s)} and sends this value of M’’ to user.

• •    User calculates M’ = M/g^f(PWDi).

• •    If M’ = M’’, then the server is accepted as legitimate; otherwise, it is rejected by the user. In this way, the server is authenticated.

Once the server has been authenticated by the user, the server needs to authenticate the user’s credentials for his legitimacy. For this, the user types in his password PWDi. After that, the smart card does the following activities:

• a.    Obtain a time sequence T from the system, which acts as the timestamp for the login purpose.

• b.    Compute the point A = (0, f(PWD i ), 0). It can be done because the password has already been typed in and f , one way function, is already stored in the smart card.

• c.    Construct line L_i passing through the points A and G; G is already stored in the smart card.

• d.    Compute midpoint, B_1, of line L_i as B₁=(G_i1/2, (f(PWD i ) + G i2 )/2, G i3 /2)

• e.    Compute another point D = (0, f(PWD_i)+f(T), 0) f. Construct the line L T passing the points D and B i . g. Choose a point H on Line L T that must be beyond the points D and B 1 .

• h. Make an authenticated message {IDT i , G, H, A 1 , T} and send it to the system. The parameter A i is already stored in the smart card in registration phase.

It may be noted that the login request is time dependent. We see that the system can construct different lines L_Ts for the same user corresponding to different time sequence T. Since our scheme is time dependent, it can withstand the replay attack. Fig. 2 illustrates the login phase for user U i graphically.

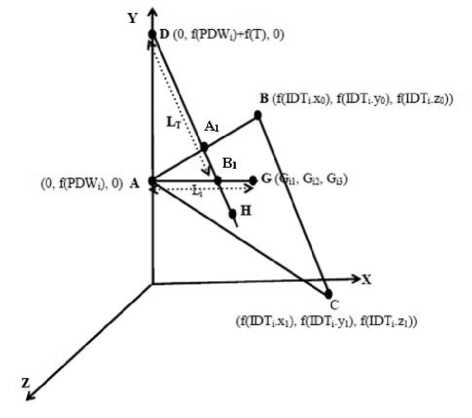
Fig. 2: Graphical representation of login phase

• ii. User Authentication Phase

Once the user has authenticated the server, he sends the authenticated message {IDTi, G, H, Ai, T} to the server. The system checks this message. If it is found valid, the user is allowed to log into the system. The system does the following activities to authenticate the login request:

• a.    Test the format of Identity IDT i . If it is incorrect, reject the login request.

• b.    Test the validity of timing sequence T. If it is invalid, reject the login request.

• c.    In this phase, the server knows both the secret keys. From these two secret keys, it computes the points B = (f(IDT i .x 0 ), f(IDT i .y 0 ), f(IDT i .z 0 )) and C = (f(IDT i .x 1 ), f(IDT i .y 1 ), f(IDT i .z 1 )).

• d.    Construct the line L_A passing though the points B and A i . The point  A 1 is already in

authenticated message.

• e.    Find the intersection point R of the line L A with y-axis as R = (0, E i , 0).

• f.   Compute the point D’ = (0, E i + f(T), 0).

• g.  Reconstruct the line L T passing through the

points D’ and H.

• h.    Find the intersection point W of the lines L_i and L_T.

• i.    If W is equal to the middle point of the line segment joining the points G and R, accept login request; otherwise reject it.

The point R will coincide with the point A and D’ will coincide with the point D in case authentication is true.

• D. Password Change Phase

For security reasons, we should change our password frequently. It is an important facility provided by any scheme. Whenever a user wishes to change his current password with a new one, the following activities take place. Assume the current password of the user U i as PWD_i and the new password as PWD_i*.

• a.    User inserts his smart card into the card reader and makes a request to change his password.

• b.    Server asks him to enter his current password PWD i and the new password PWD i * both.

• c.    Server recalculates all of the three points A, B, and C as above

• •    A = (0, f(PWD i ), 0)

• •    B = (f(IDT i .x 0 ), f(IDT i .y 0 ), f(IDT i .z 0 ))

• •    C = (f(IDT i .x 1 ), f(IDT i .y 1 ), f(IDT i .z 1 ))

• d.    Reconstruct the triangle ABC by using these points A, B, and C.

• e.    Calculate the centroid G’ of this triangle ABC.

• f.    If G = G’, then system performs the password change phase else it rejects.

• g.    Server calculates the value of f(PWD i *) and new points A’, B’, and C’ as follows:

• •    A’ = (0, f(PWD* i ), 0)

• •    B’ = (f(IDT i .x 0 ), f(IDT i .y 0 ), f(IDT i .z 0 ))

• •    C’ = (f(IDT i .x 1 ), f(IDT i .y 1 ), f(IDT i .z 1 ))

• h.    Construct the triangle using these points A’, B’, and C’.

• i.    Calculate the centroid G’’ of this triangle A’B’C’.

• j.    Replace the value of G with G’’.

In this way a user can change his password. In next section, we illustrate the above discussed phases of our proposed scheme.

• III.    Illustration

Assume the parameters P=29, g = 15, (x 0 , y 0 , z 0 ) = (2, 3, 4) and (x 1 , y 1 , z 1 ) = (5, 6, 7), and s = 19. The user chooses his password PWD i , say, 17, and presents f(PWD i ) = 13 to the central authority 9CA),that takes the following actions:

• a.  Assign IDT_i, say 8, to user U_i

• b.    Compute

o A = (0, f(PWD i ), 0) = (0, 13, 0).

o B = (f(IDT i .x 0 ), f(IDT i .y 0 ),f(IDT i .z 0 )) = (26, 3, 16).

o C = (f(IDT i .x 1 ),f(IDT i .y 1 ), f(IDT i .z 1 )) = (7, 5, 10).

• c.    Construct the triangle by using A, B, and C points.

• d.    Find centroid, G, of this triangle, i.e. G = (11, 7, 28).

• e.    Construct the line passing through the points A(0, 13, 0) and G(11, 7, 28), i.e.,

(x-0)/11 = (y-13)/-6 = (z-0)/(28-0) = k1, where k1 is an integer from GF(P).

• f.    Compute the midpoint of the line segment joining A(0, 13, 0) and B(26, 3, 16), i.e.

A 1 = (13, 8, 8) in GF(29)

• _{g.    Compute M = g}f(IDTi ⊕ s) + f(PWDi) _{= 15}f(8 ⊕ 19) + 13

mod 29 = 3

• h.    Store {8, f(.), 29, (11, 7, 28), (13, 8, 8), 3} in the smart card.

In login phase, the user types in his password PWD i as 7 and the smart card takes the following actions:

Server Authentication Phase

• •    Server calculates M’’ = g^{f(IDTi XOR s)} = 15^{f(8 ⊕ 19)} mod 29 = 13 and sends this value of M’’ to user.

• •    User calculates M’ = M/g^f(PWDi) = 3/(15¹³) = 3/27 = 3*14 = 13.

• •    Here, M’ = M’’ = 13, then the server is accepted as legitimate; otherwise, it is rejected by the user. In this way, the server is authenticated.

User Authentication Phase

• a.    Get timestamp T from the system, say, T=5.

• b.    Calculate the point A using the password: A = (0, f(PWD i ), 0) = (0, 13, 0).

• c.    Reconstruct the line L_i passing through the points A = (0, 13, 0) and G = (11, 7, 28), i.e.

x/11 = (y – 13)/(7 – 13) = z/28 = k 2

where k 2 is an integer from GF(P).

• d.    Find the middle point of A(0, 13, 0) and G(11, 7, 28), i.e., B i (20, 10, 14) in GF(29)

• e.    Suppose f(T) =14, calculate a new point D = (0, f(PWD i ) + f(T), 0) = (0, 27, 0).

• f.    Construct the line L_T passing through the points D = (0, 27, 0) and B i = (20, 10, 14), i.e.

x/20 = (y – 27)/(10 – 27) = z/14 = k 3

where k 3 is an integer from GF(P).

• g.    Choose a random point H beyond the points B and D, say, (11, 22, 28) on line L T .

• h.    Now, sends the message {IDT i , G, H, A 1 , T} = {8, (11, 7, 28), (11, 22, 28), (13, 8, 8), 5} to the server

In authentication phase, we perform the following actions:

• a.    Using the secret keys, we easily compute the point B = (f(IDT i .x 0 ), f(IDT i .y 0 ), f(IDT i .z 0 )) (26, 3, 16)

• b.    We know the value of A 1 = (13, 8, 8)

• c.    Construct the line segment L_i passing through the points A₁ = (13, 8, 8) and B = (26, 3, 16), i.e.,

(x – 13)/ 13 = (y – 8)/-5 = (z – 8)/8 = k 4

where k 4 is an integer from GF(P).

• d.    Find the intersection point R between the y-axis and the line L A : (0, E, 0) = (0, 13, 0).

• e.    Reconstruct the line L_i passing through R(0, 13, 0) and G(11, 22, 28) as:

x/11 = (y – 13)/(7 – 13) = z/28 = k 5

where k 5 is an integer from GF(P).

• f.   Calculate the point D’ = (0, E+f(T),0) = (0,27,0).

• g.  Reconstruct the line L T passing through the

points D’ = (0, 27, 0) and H = (11, 22, 28), i.e., x/11 = (y – 27)/(22 – 27) = z/28 = k6

where k6 is an integer from GF(P)

• h.    Calculate the intersection point of the lines L_i and L T ,

• i.    To find the intersection point D i of following lines

x/11 = (y – 13)/(7 – 13) = z/28 = k 5 x/11 = (y – 27)/(22 – 27) = z/28 = k 6

here, we equate the above line and get the intersection point D1 = (20, 10, 14)

• i.    Since D₁ = (20, 10, 14) is equal to the middle point of the line segment joining the points G and R, i.e., B 1 , the User U i is authenticated.

• j.    Therefore, the system will complete the login request.

• IV.    Security Analysis of Proposed Scheme

To understand the security strength of a remote logic scheme, it must withstand against the attacks. Here we discuss various attacks against which it can protect. These attacks and their protection in our scheme are discussed below.

• A.    Resistant to Offline Password Attack

The offline password attack can be due to the smart card or due to intercepting the message of the login request. In our scheme, if an adversary is able to get the user’s smart card and detects the secret information stored on it, he will not be able to guess the user password because the values stored on the smart card do not yield any combination. In case the adversary is able to intercept the user login request and the response message of the server, he cannot guess the password because the login request contains no information about the password. Similarly, the password cannot be guessed from the response message sent by the server in verification phase. If some adversary has smart card and intercepts the message of the login request, he cannot detect the valid password of the user by using the contents of the smart card and the login request message because it is very difficult to guess the password as calculating B = (f(IDT i .x 0 ), f(IDT i .y 0 ), f(IDT i .z 0 )) and C =(f(IDT i .x 1 ), f(IDT i .y 1 ), f(IDT i .z 1 )) is extremely difficult. Furthermore, these values are neither stored alone in the smart card nor transmitted a the public/insecure network.

• B.    Resistance to Insider Attack

While giving the password to the server in registration phase, an insider, who may be a server administrator itself, may masquerade as the user to access other server. In that case, in our scheme, the password cannot be obtained because in registration phase the user does not provide his password to the server, rather he provides his identity and the encrypted value of the password. Furthermore, the user has a facility to change his password (from time to time), especially, the default password. Thus, our scheme can withstand the insider attack.

• C.    Forged User Attack

In order to get the user information, an adversary acts as a valid user. In that case, he can send a valid login request to the server in authentication phase. Since the adversary has no information about B i , he cannot complete the login request successfully. Even if he does some changes in login phase, he cannot complete the authentication phase because the received values are different from the calculated ones.

• D.    Forged Server Attack

In a forgery attack, a illegal user pretends to be a legal user. If an adversary acts as a valid server, he must be able to compute the valid value of G’’; but he cannot do so due to lack of access. In case he modifies the value of G’’ by assuming the value of x, he will not be able to do so because the received value of G’’ is different from the original one. Thus, our scheme is resistant to the forgery server attack.

• E.    Resistance to Server’s secret Key Guessing Attack

This attack can be performed if an adversary somehow gets the smart card. The smart card stores the secret keys (x0, y0, z0) and (x1, y1, z1) by using one-way function, besides other parameters. In case the smart card has been stolen by the adversary, he cannot get the secret keys. In case the adversary has also got login request message, he, knowing the values of H and G, cannot calculate the value of the secret keys. Thus, our scheme is resistant to the server’s secret key guessing attack.

• F.    Resistance to Denial of Service Attack

In denial of service attack, a legal user is not allowed to use the system resources or access the system data. Since all information stored in the smart card cannot be changed, the adversary cannot modify the information stored in the smart card with the false verification number and the false password for the next login request in case he is able to steal the smart card.

• G.    Resistance to Modification of Account Database

In our scheme, the server maintains an account database in which the user’s identity and B i are stored. In case this database is modified by anyone, it can easily be detected by the server as this database has been signed using the server private key and it is regularly verified by the server. If the server detects any change in the database, which is not authentic; it restores the database using the offline backup, which is assumed to be well protected.

• H.    Resistance to Impersonation Attack

In an impersonation attack, a person tries to forge the legal identity and password of a user. Suppose an adversary is able to get the login request message {IDT i , G, H, A i , T} in authentication phase. If 2G is valid G, the adversary can send {2IDT i , G, H, A i , 2T} at 2T to login as IDT i . Since the IDT i uniquely identifies a user, the 2IDT i is an invalid user IDT i that results rejection of the login request. The login time 2T will not satisfy T c - T ≤ ∆T and hence the login request will be rejected by the server. In verification phase, the calculated values of E+f(T) will not be equal to the original value and hence the request will be rejected by the server.

• V.    Conclusion

In this paper, we have discussed a new authentication method based on 3-D Euclidean Geometry. First of all, it performs one time initialization phase in which an environment is created by using a central authority. It is used to log into a server located at far distance in a different city and also the server can verify a user for its legitimacy. For becoming a legitimate user, the new user needs to first register with the system one time. The user can verify the legitimacy of the server located in a far distant city. This scheme has low computational cost and simplicity; and thus can be suitable for practical implementation. It has a feature of mutual authentication, that is, the server is authenticated to a user and a user is authenticated to the server. It is resistant to the forged server attack and provides the flexibility to change the password. This scheme withstands many attacks like impersonation attack without involving any complex calculations.