A Benchmark for Performance Evaluation and Security Assessment of Image Encryption Schemes

Advances in technology have affected cheap access to digital storage and multimedia processing and capturing devices. Multimedia capturing devices are not restricted to cameras or camcorder but smartphones, laptop’s, tablets and other devices or everyday use are equipped with digital cameras. Moreover, access to the free or cheap internet, 3G, and 4G cellular networks has caused a large increase in internet users. These unsecured public networks are used frequently for multimedia communication. Wireless communication, on the other

Manuscript received July 20, 2016;

hand, is a big troublemaker in security. Satellite communication or other wireless technologies provide wire-free access to remote terminals through VSAT and other technologies. With the increasing trend of communication over public channel and growth of digital multimedia devices, the need for methods to protect this data from unauthorized access is becoming crucial.

Three common methods are used for security of digital images from unauthorized access or copyright violation. Image cryptography is a technique, which allows visual information to be transformed into such a form that encrypted image become unintelligible. Steganography and watermarking, on the other hand, does not encrypt the actual image but hide some other media in an image in such a way that it becomes invisible. Digital steganography encodes a secret message (pictures, text, etc.) that it becomes imperceptible for others. The image may seem to be a simple photograph but it contains an invisible secret message. The discovery of this secret message by an investigator is very difficult and can be recovered by intended recipient having the embedding algorithm and secret key. Digital watermarking is much similar to steganography in working but its application is different. It focuses on authentication of digital media and protection of intellectual property rights. A watermark image is inserted into a cover image, which is later detected or identified for copyright claim or authentication purpose. Watermarking provides the way to ensure intellectual property rights and keep track of the quick and inexpensive distribution of digital media over the internet.

Digital image encryption transforms an input plaintext image to an output ciphertext image through the cryptographic algorithm with the help of a secret key. The ciphertext image is not usable unless the decryption algorithm and secret key are available. There are numerous cryptographic algorithms and their categorization is made based on certain parameters. Two categories of the cryptographic algorithm based on secret key are; private key cipher and public key cipher [1]. In private-key cipher, the secret key is same for encryption and decryption processes. Private-key ciphers are also known as symmetric cipher. While in public-key cipher, the secret key is different for encryption and decryption processes and are not related to one another [2]. The secret key used for encryption is made public so anyone can perform encryption but only the intended recipient having the secret key can decrypt the image. This type of cipher is also known as non-symmetric cipher [3-4].

There are three categories of image encryption algorithms based on the mechanism of operation. Transposition based cipher simply work with rearrangement of pixels with a complex regular system. It has been demonstrated that all type of permutation only cipher, which works with rearrangement of pixel position, can be broken [2] . However, it can be combined with other techniques to make it more complex and cryptographically secure.

Visual transformation, on the other hand, encrypts images by dividing them into several shares (layers). These shades are positioned mechanically in such a way to reveal the original image (message). This same technique is extended to digital images for visual encryption and decryption process requires all the shares and their exact orientation for decryption. This way of encryption has very limited application and mainly used for binary images.

Value transformation based cipher has the diversity of encryption schemes. They work by modifying the gray value of pixels either in transform domain or in the spatial domain. Spatial domain based techniques operate at the bit level to change pixel value. This bit level change may be through shuffling the pixel bits or changing the quantization. Transform domain methods involve operation in DCT, DFT or DWT domain operation on coefficient. Popular techniques discussed in the literature are either value transformation based or the hybrid of above mentioned encryption methods.

Owning to the fact, numbers of encryption schemes presented in the literature are not tested for all parameters of cryptographic security and performance. A decent encryption scheme must fulfill all the security requirements of an image cryptosystem. The performance should be comparable to other proposed schemes or must be acceptable with respect to a particular application. Moreover, image encryption schemes are characterized distinctly from text, as they have to take account of the redundancy in images. Several image encryption schemes take benefit of this redundancy and encrypt the image in such a way that decrypted image is not the exact replica of input plaintext image. This recovered image is perceptually similar to the plaintext image but it may have minor changes. So a benchmark for quality analysis of recovered image should be established which would be helpful in comparison.

• A. Types of Cryptographic Attacks

Ciphertext-only Attack

Ciphertext-only attack is a cryptanalysis method where the attacker has access to only a set of ciphertext. The attack is considered successful if the attacker is able to deduce the key or even the plaintext.

Known Plaintext Attack

Known plaintext attack is a cryptanalysis method in which the attacker has information of a set of plaintext and their corresponding ciphertext. These types of attacks are more successful in the deduction of secret keys.

Chosen Plaintext Attack

Chosen plaintext attack is a category of cryptanalysis in which the attacker has access to the encryption scheme as a black box. In this way, the attacker can get ciphertext of any random plaintext. The goal of such attacks is to deduce the relationship of plaintext to ciphertext by providing specific plaintext.

Chosen Ciphertext Only Attack

Chosen ciphertext only attacks are mostly used in public key cryptosystems. In this attack model, the attacker can choose a ciphertext and get its corresponding decrypted plaintext.

Brute Force Attack

Brute force attack is employed when the attacker is unable to get any advantage of other weaknesses. It is also referred to as, exhaustive key search, as it practically checks all the possible keys for decryption. This attack can be theoretically used against any ciphertext but the limitation arises with the computational time required to perform an exhaustive key search.

Section-II presents the image encryption schemes containing three image encryption schemes which are to be analyzed for security and performance assessment. Section-III presents the metric of image quality describing four image quality measurement metrics along with tabulated and graphical representation of their testing on the selected image encryption schemes. Section-IV presents the metrics to evaluate the cryptographic security of the image encryption schemes. The section discusses the information entropy analysis, correlation coefficient analysis in the planner and 3-D view. The differential analysis presents the measurement of avalanche effect, mean squared error, number of pixels change rate, universal average change intensity, dispersion test analysis. The statistical analysis presents histogram analysis, maximum and irregular deviation measurements. Keyspace analysis presents exhaustive key search and key sensitivity test. Robustness tests include tamper detection, compression friendliness and noise tolerance. Section-VI draws the conclusion.

• II.    Image Encryption Schemes

Numerous image encryption techniques are presented in the literature with surprising characteristics. These techniques lack evaluation on common criteria. Three of these techniques are chosen for evaluation. First of these ciphers is AES based block cipher with demonstrated cryptographic security. Second, one is a compression and noise tolerant cipher and the third is a chaos-based image cipher with high randomness and unpredictability.

• A.    Advanced Encryption Standard

  National Institute of Standards and Technology (NIST) selected Rijndael as Advanced Encryption Standard (AES) in 2011 [5]. The selection of AES was a tradeoff between performance, efficiency and overall security. It replaced the Data Encryption Standard (DES) and Triple-DES due to their weaker security against brute force attacks. It is a new generation symmetric block cipher with key sizes of 128, 192 and 256 bits. It is a linear transformation

substitution cipher, which uses triple discrete invertible uniform transformations. It has a high degree of modular design, making it possible to counter any future attack mechanism or to introduce development. The algorithm has outperformed in 15 candidates for AES but has received criticism by some researchers due to its security. These criticisms are theoretically valid as the other algorithms provide better security but it does not mean that AES encrypted data is vulnerable to attack. Although it is not the most secure cipher but its security can be increased by adding more rounds.

• B.    Compression and Noise Tolerant Image Encryption Scheme

Nisar et. al [6] proposed a compression and noise tolerant image encryption scheme. They have used orthogonal basis vectors to process the image to introduce confusion in the algorithm. The image is separated into 16×16 blocks and these blocks are permuted. These permuted blocks are DCT transformed and multiplied with orthogonal vectors generated from Singular Value Transformation (SVD) of a randomly generated matrix. The resultant cipher image has the horizontal correlation, which allows it for lossy compression.

• C.    Chaos-based Image Encryption Scheme

Ruisong Ye [7] has used generalized Bernoulli shift maps to permute the image pixel position and change the grayscale values. Two chaotic orbits are generated for the permutation of image pixels and diffusion of image grayscale value. The first chaotic sequence is used to get an index sequence to permute the pixel positions. The second chaotic sequence is generated from generalized for of Bernoulli shift map by setting the initial values. Every cipher pixel of cipher image is obtained by taking XOR of plain image pixel with randomly generated pixel (through Bernoulli shift map) and the previous cipher image pixel multiplied by the mod of gray-level. The cipher has demonstrated high-security characteristics with a large key space.

• III. Image Quality Metric

There are some image encryption schemes which doesn’t exactly reproduce the decrypted image and add slight distortion which is tolerable in some conditions if the visual quality of the image is not significantly degraded. Image quality metric describes the metrics which can be used to quantities the recovered image quality as compared to the original image.

• A.    Normalized Correction

It is a function of time lag to measure the similarity between two images. A numerical value of 1 indicates an identical image and deviation from unity indicates the difference between the two images. The formula for calculation of NC is provided below.

м

N С (Х,Х' ) = ^.^

' ^х(U ) * ^xq,j)

; ТМЖ ,j))2

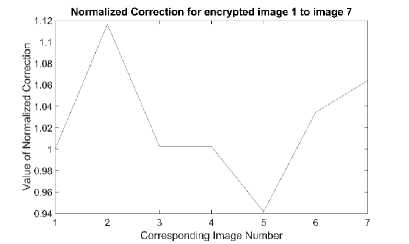
Fig.1. Normalized Correction Measurements between Original and Recovered Images by Cipher2.

Fig. 1 shows the result of normalized correction for Cipher2 [6] for seven test images used for analysis. Numerical values of NC for Cipher1 are presented in table 2. The results of NC for Cipher1 [5] and Cipher3 [7] were unity so their numerical results are provided in table 1.

• B.    Correlation Measure

The correlation coefficient can be used to measure the similarity between two images. It measures the crosscorrelation between pixels of original and recovered. This test can provide numerical results to quantize the similarity measure and the graphical results will demonstrate the same correlation graphically. A diagonal line of points will indicate identical image, the spreading of points above and below this line will designate the amount of variance between two images.

Fig. 2 shows the cross-correlation of plaintext image and recovered image by Cipher2 [6]. Numerical results of cross-correlation for the other images generated by Cipher2 [6] are provided in table 2 and table 1 provides the similar values for Cipher1 [5] and Cipher3 [7].

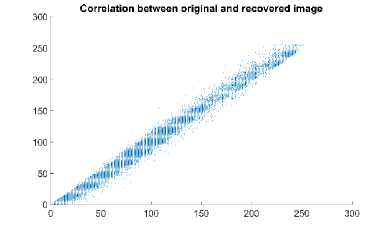
Fig.2. Cross-Correlation between the Original Image (Archer) and Recovered Image with Cipher2.

• C.    Mean Squared Error

MSE provides the mean of the squares of the differences of the corresponding pixels of two images. It provides a numerical value of distortion in the recovered image. Below formula is used to calculate MSE between original and recovered image.

м․S․Е=1∑(Х(_Х ∗) 2              (2)

п i=i

Fig.3. The Mean Squared Error between Original Images and Recovered Images with Cipher2.

Fig. 3 provides the results of MSE between original and recovered image for Cipher2 [6]. Numerical values of it are provided in table 2. Table 1 provides the numerical values of MSE for Cipher1 [5] and Cipher3 [7].

• D.    Peak Signal-to-Noise Ratio (PSNR)

PSNR provides the peak of error between two images. It is an estimator for human visual perception of reconstruction quality. It is the most commonly used metric to check the recovered image quality. In some situation, PSNR may not produce actual results correlating with human visual perception [8]. We can calculate PSNR by the following formula.

/МАХЛ

PSNR=10logю( MSE )          (3)

Fig. 4 shows the result of PSNR for original and recovered image by Cipher2 [6], the same is provided numerically in table 2. Table 1 provides the values of PSNR for Cipher1 [5] and Cipher3 [7].

Fig.4. PSNR for Original and Recovered Images with Cipher2.

• E.    Structural Similarity Index

SSIM is intended to improve the similarity measure based on human visual perception on traditional methods such as PSNR and MSE. It differs from other techniques as it considers image quality degradation as observed variance in structural information. SSIM is based on the idea that the pixels have a strong relationship with its neighbors and this relationship has important information about the structure of objects. Moreover, SSIM is only applied to luminosity layer of the TrueColor image as all the structural information is contained in this layer. SSIM can be calculated from the following formula.

(2ЦхЦу + С1)(2^ху + с2 )

( м2 + Цу + С1)(Оу + о'у + с2 )

Where

Цх the average of X & Цу the average of У .

^i =( k^L )², С2 =( ^•2^)² two variables to stabilize the division with weak denominator

L the dynamic range of the pixel values ki = 0․01 and к2 = 0․03 by default.

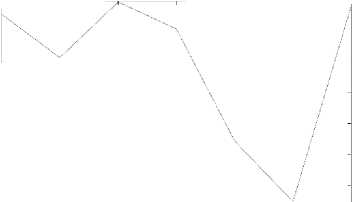
Numerical results of SSIM are used for similarity evaluation, higher value indicates more similarity and a value of 1 is achieved in the case of identical images.

SSIM for encrypted image 1 to image 7

0,95

0.94

"й 0.93

0.92

Corresponding Image Number

Fig.5. SSIM for Original and Recovered Images with Cipher2.

Fig. 5 shows the results of SSIM for original and recovered image by Cipher2 [6]. Numerical values of the same are provided in table 2. Table 1 provides the numerical values of SSIM for Cipher1 [5] and Cipher3 [7].

Table 1. Numerical values of NC, CC, MSE, PSNR and SSIM for test images for Cipher1 and Cipher3.

Image	NC	CC	MSE	PSNR	SSIM
Archer	1.0000	1.0000	0.0000	Inf	1.0000
Flower	1.0000	1.0000	0.0000	Inf	1.0000
Glider	1.0000	1.0000	0.0000	Inf	1.0000
Kodim15	1.0000	1.0000	0.0000	Inf	1.0000
Lena	1.0000	1.0000	0.0000	Inf	1.0000
Mandrill	1.0000	1.0000	0.0000	Inf	1.0000
Peppers	1.0000	1.0000	0.0000	Inf	1.0000

Table 2. Numerical values of NC, CC, MSE, PSNR and SSIM for test images for cipher2.

Image	NC	CC	MSE	PSNR	SSIM
Archer	1.0004	0.9978	22.4941	34.6101	0.9857
Flower	1.1164	0.9917	113.3242	27.5983	0.9715
Glider	1.0025	0.9978	16.3242	36.0025	0.9896
Kodim15	1.0022	0.9958	23.8359	34.3585	0.9809
Lena	.9416	0.9963	243.2791	24.2698	0.9443
Mandrill	1.0342	0.9688	190.0615	25.3419	0.9246
Peppers	1.0639	0.9976	91.4748	28.5178	0.9883

• IV.    Benchmark for Cryptographic Security Evaluation

Visual examination of ciphertext image is the primary factor to quantify the encryption quality of an image encryption scheme. Nevertheless, visual examination is not enough to judge the quality of encryption. Thus, an evaluation benchmark is required to estimate the encryption quantitatively. An effective image encryption algorithm changes the pixel values in such a way to make it irregular. Thus, higher the change in pixel values, the more effective is the encryption.

Following are the performance metric to evaluate the cryptographic security of encryption scheme.

• A.    Information Entropy Analysis

Information entropy is a mathematical parameter of information and coding theory, which reflects randomness and uncertainty of a source. It gives information about the source itself [9, 10]. It is an important concept for analyzing any cryptosystem as it measures its uncertainty and randomness. The entropy of a source can be calculated by following formula [11-15] :

2^-1

Н(s)=-∑ Р(Si)log2Р(Si )         (5)

1=0

Here, S is the source, P(Si) is the probability of occurrence of symbol Si, N is the number of bits to represent symbol Si. For an ideally random source with 2N symbols, the entropy is N. Therefore, for a grayscale ciphertext image, the ideal entropy should be 8. An actual information source is never actually random so its entropy value is smaller than the ideal one. However, in an actual cryptosystem, the entropy must be as closer to the ideal value as possible otherwise; it will threaten the security of the cryptosystem.

Table 3. Information Entropy Analysis of Three Encryption Schemes

	AES	FEA	Chaos
Archer	7.9997	7.1127	7.9991
Flower	7.9998	7.0432	7.9991
Glider	7.9998	7.0656	7.9989
Kodim15	7.9998	7.0415	7.9991
Lena	7.9998	6.9828	7.9991
Mandrill	7.9998	7.0925	7.9991
Peppers	7.9998	7.1482	7.9992

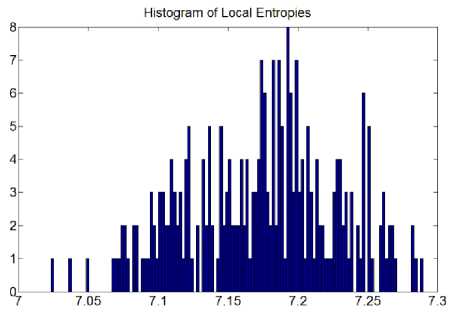
Fig.6. Histogram of Local Entropies for Cipher1: Archer Image

Histogram of Local Entropies

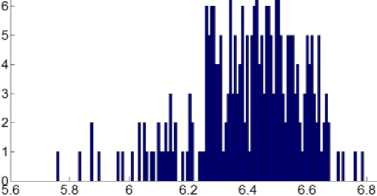
Fig.7. Histogram of Local Entropies for Cipher2: Archer Image

Moreover, the entropy of the source is not uniformly distributed so we have also calculated the local entropy. Local entropy is displayed graphically by calculating entropy for 16×16 blocks of cipher image and plotting their histogram.

Histogram of Local Entropies

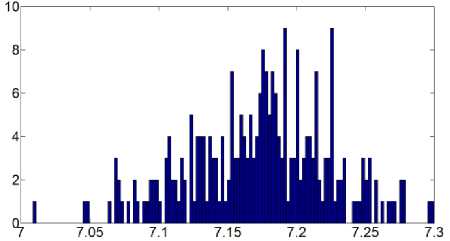
Fig.8. Histogram of Local Entropies for Cipher3: Archer Image

• B.    Correlation Coefficient Analysis

Correlation determines the degree of similarity between two variables. It is used as an important metric to evaluate the quality of a cryptosystem [16, 17]. Natural images have a lot of correlation between their adjacent pixels as there are very few sharp edges [12]. The image cryptosystem is regarded as effective if it hides the original image content completely with the lowest correlation [11, 16, 18]. Correlation coefficient for an identical image is equal to one (-1 for negative image) and for a highly uncorrelated image is almost zero. Correlation of an images can be calculated in horizontally adjacent pixels, vertically adjacent pixels and diagonally adjacent pixels. Mathematically, the correlation coefficient is calculated by below formulas [2, 11-13, 16, 17, 19, 20].

С о v (х, у)

7 УЛR(x) х 7УЛR(у)

1 N

VAR (x)=-^(xi-E(x))

1 N

Cov(х,у) =  У (xt -E(x))(yt -E(y))

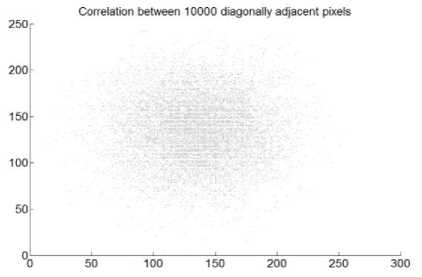
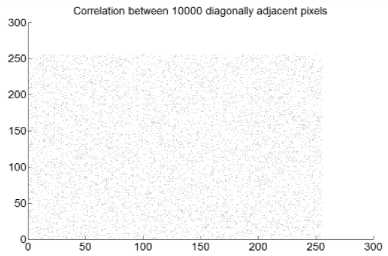
Fig. 9-11 provides the correlation plot of Archer image encrypted by the three ciphers. The plot of correlation between all the pixels in diagonal, horizontal and vertical directions are provided for comparison.

Here, C.C is correlation coefficient, x and y are the pixel values, Cov is the covariance between x and y, VAR(x) gives the value of variance at pixel value x, δ x is standard deviation, N is the total number of pixels and E is expected value operator.

(a)

(a)

(b)

(b)

(c)

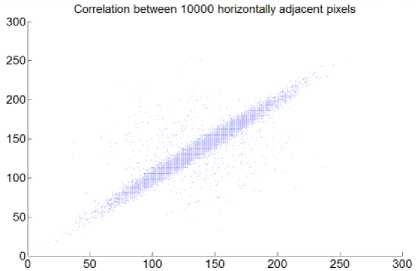
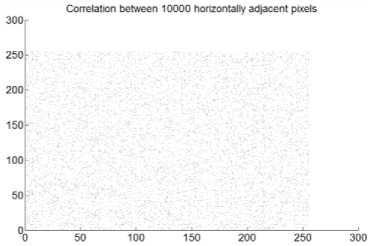
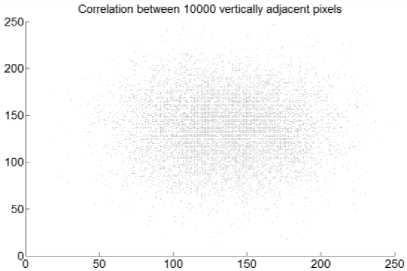
Fig.10. Correlation Coefficient Analysis of Archer Image Encrypted Using Cipher2: (a) Correlation between Diagonally Adjacent Pixels (b) Correlation between Horizontally Adjacent Pixels (c) Correlation between Vertically Adjacent Pixels

Correlation between 10000 vertically adjacent pixels

(a)

(c)

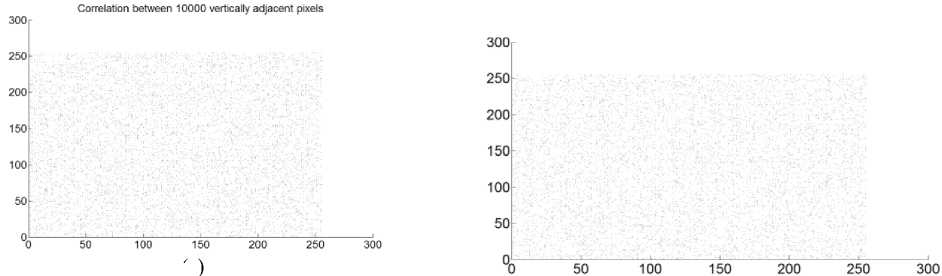
Fig.9. Correlation Coefficient Analysis of Archer Image Encrypted Using Cipher1: (a) Correlation between Diagonally Adjacent Pixels (b) Correlation between Horizontally Adjacent Pixels (c) Correlation between Vertically Adjacent Pixels

Correlation between 10000 horizontally adjacent pixels

50-

°0       50       100      150      200      250      300

(b)

Correlation between 10000 diagonally adjacent pixels 300-                                      ~

250 200 150 100

50-

°0        50       100      150      200      250      300

(c)

Fig.11. Correlation Coefficient Analysis of Archer Image Encrypted Using Cipher3: (a) Correlation between Diagonally Adjacent Pixels (b) Correlation between Horizontally Adjacent Pixels (c) Correlation between Vertically Adjacent Pixels

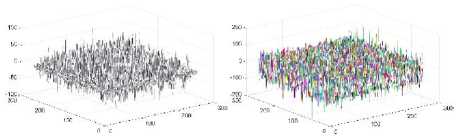
The gradient is another measure of image correlation. In a highly correlated image, the value of gradient will be very less and its 3D plot will be a plane surface. Fig. 12 provides the result of the gradient plot for plaintext Archer image and its corresponding cipher images by the three ciphers under test. Fig. 12 (a) provides the gradient map for plaintext cipher image which clearly shows homogeneous areas on the left. Fig. 12 (b) shows the same graph for cipher image of Cipher1, which indicates highly non-homogeneous distribution. Fig. 12 (c) on the other hand indicate homogeneity at some areas and nonhomogeneity at the other places. It accounts for the same correlation which is indicated in Fig. 10 (b). Fig. 12 (d) has the same plot as (b) but its color distribution is much wide and provides better no-homogeneity.

(a)

(b)

Table 4. Numerical Results Of Correlation Coefficient Analysis For Archer And Kodim15 Images.

	Cipher1 [3]	Cipher2 [4]	Cipher3 [5]
Archer (diagonal)	0.0018	0.0078	0.0169
Archer (vertical)	0.0028	0.0035	0.0097
Archer (horizontal	0.0094	0.9199	0.0087
Kodim15 (diagonal)	0.0106	0.0473	0.0055
Kodim15 (vertical)	0.0086	0.0557	0.0132
Kodim15 (horizontal)	0.0108	0.9143	0.0007

(c)

(d)

Fig.12. (a) Plain image (Archer) (b) Cipher image with Cipher1 (c) Cipher Image with Cipher2 (d) Cipher Image with Cipher3

• C.    Differential Analysis

  The differential analysis is based on the study of change in output pixels in response to a change in input pixels. This property of an image cryptosystem is referred as diffusion characteristics and was introduced by Shannon in his classical masterpiece in 1949 [9]. To withstand the differential cryptanalysis, a cryptosystem must ensure good diffusion characteristics. The output image should change entirely in an unpredictable manner for a change of single pixel of an input image. Following parameters are used to perform differential analysis of a cryptosystem to ensure good diffusion characteristics.

Avalanche Effect

Avalanche effect is used to measure the diffusion characteristic of an image cryptosystem, which is an important parameter that must be checked to verify the randomness and complexity of the system. The system is taken as a black box and one bit of the input plaintextimage is changed to observe the change in the output ciphertext-image. Small change in output image in response to 1-pixel changed input image will make it possible to construct a meaningful relationship between the two images. To avoid deduction of this relationship, the output image pixels of 1-pixel changed image must be more than 50% different from the original image. Let C1 is the cipher image with original plaintext image and C2 is the cipher image with a 1-pixel change in the plaintext image. Following are the test to measure the avalanche effect.

Table 6. Avalanche Effect (MSE, NPCR, and UACI) Results for Cipher2

	MSE	NPCR	UACI
Archer	-16.0760	99.9993	0.0129
Flower	-15.8515	99.9985	0.1292
Glider	-16.7518	99.9989	0.0459
Kodim15	-15.5447	99.9985	0.0523
Lena	-17.7328	99.9985	0.0408
Mandrill	-16.7046	99.9969	0.0459
Peppers	-15.8838	99.9985	0.0502

Table 5. Avalanche Effect (MSE, NPCR, and UACI) Results for Cipher1

	MSE	NPCR	UACI
Archer	40.3882	99.6216	33.5271
Flower	40.3877	99.6071	33.4798
Glider	40.3994	99.6147	33.5221
Kodim15	40.3778	99.6140	33.4387
Lena	40.3755	99.6040	33.4929
Mandrill	40.3781	99.6143	33.3709
Peppers	40.3837	99.6403	33.4227

Table 7. Avalanche Effect (MSE, NPCR, and UACI) Results For Cipher3

	MSE	NPCR	UACI
Archer	40.4000	99.5972	33.3052
Flower	40.3997	99.6918	33.5325
Glider	40.4338	99.6735	33.7354
Kodim15	40.4235	99.6887	33.6324
Lena	40.3978	99.6338	33.6025
Mandrill	40.4083	9.6063	33.6323
Peppers	40.3758	99.6078	33.4130

Mean Squared Error (MSE)

Mean Squared Error is used to check the avalanche effect by calculating MSE between image C1 and C2 [19, 20] . MSE >30 dB indicates an evident difference between two images and their relationship is too complex to be predicted easily [23, 24] .

Number of Pixel Change Rate (NPCR)

The number of Pixel change rate is a test to measure the avalanche effect of an image cryptosystem. It measures the number of pixel difference between two cipher images C1 and C2. The theoretical critical value for this test is 99.6094% for 8-bit image [25] .

NPCR =∑ -- ∑ ^D (‘ ,2)×100        (9)

M×N

Universal Average Change Intensity (UACI)

Universal average change intensity measures the average intensity difference between the two images. Theoretical critical value for this test is 33.4635% [25] .

=

M × N

∑ и ∑ 7=i | т_г ( i , 7 )- m₂ ( i , 7 )|

^*            256

Dispersion Test Analysis

Dispersion test is performed to check the result of diffusion. A white image with a small black patch of 8×8 and a black image with a small patch of 8× 8 white color are encrypted and the results of dispersion are checked in the output image.

Table 8. Entropy Analysis of White Image (With 8x8 Black) and Black Image (With 8x8 White)

	Cipher1	Cipher2	Cipher3
Black Image	7.9993	0.0007	7.9968
White Image	7.9994	0.0012	7.9971

• D.    Statistical Analysis

Histogram Analysis

Image histogram shows the distribution information of pixel values and discloses statistical characteristics. It is regarded as an important statistical feature of an image and is taken as a metric for evaluation of the security of an image encryption scheme. In Shannon’s perspective

[9], image ciphers can be attacked by statistical analysis. An image cipher should transform a meaningful and correlated image into a random looking image. Therefore, an image cipher should produce an encrypted image with uniform histogram distribution.

Color image histogram is unlike the histogram of a grayscale image (intensity histogram). Usually, histogram for three RGB color channels is obtained separately and visually inspected for uniformity [12 , 17 ]. Sometimes, the brightness is taken out by normalizing all the triplets and then plotting them sequentially. Aberration graphs are also used for image histogram analysis as they plot the intensity values in three dimensions [26 ]. The purpose of aberration graph can be served with a gradient map of Fig. 12. These techniques are simple but not effective for efficient histogram analysis of color images. A technique for drawing color histograms and color clouds originally developed for movie poster analysis by S.C. Gaddam [27 ] is presented here for histogram analysis of cipher images. Fig. 13-15 provides the color histogram for Archer image encrypted by the three ciphers. The histogram analysis of Cipher1 and Cipher3 fulfill the uniformity requirement whereas of Cipher2 is debatable.

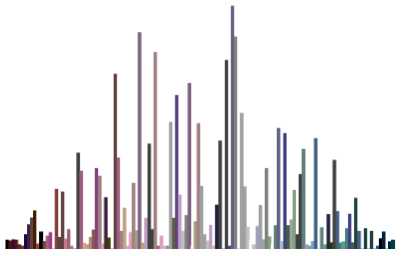
Fig.14. Color Histogram of Archer Image encrypted by Cipher2

Fig.13. Color Histogram of Archer Image encrypted by Cipher1

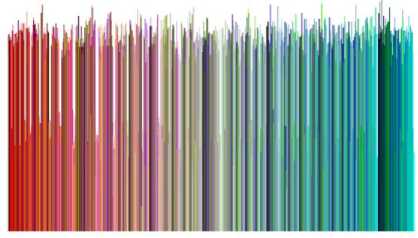
Fig.15. Color Histogram of Archer Image encrypted by Cipher3

Maximum Deviation

A parameter to check the statistical security of encryption is the maximum deviation, which measures the deviation between pixel values of an original image and the encrypted image [16 , 19 ]. Higher the value of maximum deviation more is the deviation in encrypted image from that of plaintext image. Below formula is used to calculate the value of maximum deviation.

254 d₀ + ^255 , V ,

D _{=    2   +}∑ d_t           (11)

t=i

Here, di is the difference of histogram of the original image and that of cipher image at value i. d0 and d255 are the difference values at index 0 and 255.

Table 9. Results of Maximum Deviation for the Image Ciphers

	Cipher1	Cipher2	Cipher3
Archer	77357	67159	48439
Flower	122880	111430	96096
Glider	97164	77738	55346
Kodim15	110380	90674	79296
Lena	54894	33210	22330
Mandrill	44518	22014	21718
Peppers	73422	44004	23318

Irregular Deviation

Maximum deviation alone is not enough to ensure statistical randomness of a ciphertext image. The encryption algorithm should randomly change the pixel values to become a statistically robust scheme [16 , 19 ]. An algorithm, which makes a large change in some image pixel values and produces insignificant change in other, is not statistically secure. The procedure to calculate the value of irregular deviation is enlisted below.

Take the histogram; say h, of absolute difference of plaintext image and ciphertext image.

Calculate the mean value of h and name it Mh.

Calculate the irregular deviation ID using the following formula:

Id =∑|ℎ i ^- M_h |              (12)

i=o

• E.    Keyspace Analysis

Keyspace analysis is done to check robustness against brute force attacks. A good image encryption system should have large enough key space and high sensitivity to the secret key.

Exhaustive Key Search

Key space size is the number of different keys, which can be used as secret key. Sufficiently large key space is necessary to prevent the execution of brute force attacks [13 , 16 ]. Exhaustive key search is the number of operations required to check all the possible secret keys for decryption [16 ]. A cryptosystem with 256_bits key will require 2²⁵⁶ number of operations to check all the keys. Table 12 provides the key space size for the three encryption schemes, which is large enough to be secure against brute-force attack.

Table 11. Key size for the Encryption Schemes

Encryption Scheme	Key Size (bits)
Cipher1	128, 192, 256
Cipher2	128
Cipher3	312

Key Sensitivity Test

Key sensitivity is an extreme dependency on the exact key. This test measure, how much the cryptosystem is sensitive to small change in secret key [13 ]. A secure cryptosystem, even 1-bit change in the secret key would be enough to produce entirely different cipher image. Key sensitivity is checked in two different aspects: (a) completely different ciphertext images should be produced with 1-bit change in secret key, (b) 1-bit changed secret key should produce entirely random decryption image. The satisfactions of these two aspects of key sensitivity test are mandatory for the security of key space [13 , 20].

• F.    Robustness Test

Image robustness tests are used to check the dependence of decryption algorithm on the exact values of ciphertext image. The success of these tests indicates higher security but reduces the robustness to compression, noise, and small unintentional tampering.

A smaller value of ID indicates the histogram is close to uniformity and betters the statistical properties of encryption.

Table 10. Results of Irregular Deviation for the Image Ciphers

	Cipher1	Cipher2	Cipher3
Archer	60404	55292	47652
Flower	64704	53660	40128
Glider	72376	65086	53768
Kodim15	59490	56654	42396
Lena	74780	69920	59694
Mandrill	81680	74974	64776
Peppers	69736	64428	56462

(a)                          (b)

(c)                          (d)

Fig.16. Image Decryption Results with 1bit changed Secret Key (a) Plaintext Archer Image (b) Decryption Results with Cipher1 (c) Decryption Results with Cipher2 (d) Decryption Results with Cipher3

Tamper Detection

This test is performed to check the robustness against tempering in ciphertext image. It indicates high diffusion characteristics of an image cryptosystem. A small patch of 8×8 is painted black in the cipher image and the decryption is performed to check the robustness against tampering [26] . The same can be done by changing the least significant bit of cipher image. Corresponding change between decrypted image and non-tempered decrypted image is checked for compliance [12 ].

same image. Huffman coding, run-length coding, arithmetic coding, LZW coding and Simplified MED are some types of lossless compression [29, 30]. The second type of compression is lossy compression, which reduces the amount of data that is not necessary for visual inspection. Under-sampling, reduced color maps, requantization and other such techniques are used as a mean of lossy compression. Lossy compression hence introduces small variations in the cipher image so an algorithm positive to cipher image sensitivity test or cut test will not be friendly to lossy compression. The compressed image produced with such encryption algorithm cannot be recovered with accuracy.

If an algorithm produces good quality image after decryption of its compressed image and provides significant compression is said to be a compression friendly encryption algorithm. If the cipher image has high entropy, it would not result in compression as there is not enough correlated data to be compressed. In some cases, if a highly uncorrelated ciphertext image is compressed by JPEG it may result in an increase of image size [29 , 31]. There are some encryption algorithms, which perform compression before or during the process [29 ].

(a)                           (b)

(c)                          (d)

Fig.17. Temper Detection Results with 8x8 painted box (a) Original

Archer Image (b) Recovered with Cipher1 (c) Recovered with Cipher2 (d) Recovered with Cipher3

Compression Friendliness

Image compression has vital importance in the field of cryptography. It reduces the transmission or storage bandwidth significantly making it a highly desirable property. Numerous image compression algorithms are in practices, which are developed, based on information theory [9]. There are two types of image compression methods; lossless and lossy. Lossless compression reduces the unnecessary redundancy in the image by reducing the required number of bits to represent the

Compression Rate (JPEG quality factor)

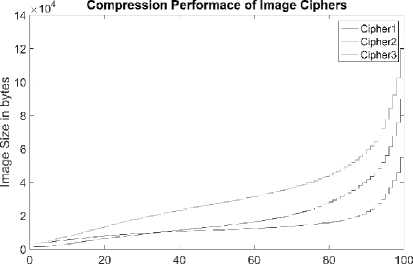
Fig.18. Compression Performance of Image Ciphers using Archer Image

Fig. 18 shows the reduction in cipher image size after JPEG compression. Highest compression ratio is achieved in the case of Cipher2 whereas Cipher3 provides minimum compression ratio. Fig. 19 provides the result of decryption after JPEG compression with QF of 90. Cipher1 fails to recover the image whereas Cipher2 has recovered the image with reasonable visual quality. Recovery with Cipher3 contain visible distortion but can be tolerated in special cases.

(c)

(d)

Fig.19. JPEG compressed image recovery results (QF=90%) (a) Archer Image (b) Cipher1 recovery (c) cipher2 recovery (d) cipher3 recovery

Noise Tolerance

Image after encryption may go through a noisy channel and certain amount of noise can be introduced. Tolerance of the cryptosystem to such noise becomes a desirable property in some applications. It is true that such property will indicate some weakness in the encryption scheme but it can be dealt with that specific application. AWGN is added to the ciphertext image, it is decrypted with the exact decryption key, and its similarity with the uninterrupted recovered image is tested for compliance.

(a)                           (b)

(c)                         (d)

Fig.20. Noise Immunity Result with AWGN (mean 0, variance 0.01) (a) Archer Image (b) Cipher1 recovery (c) cipher2 recovery (d) cipher3 recovery

Cipher1 is highly insensitive to distortion as it is evident from Fig. 20 (a). Distortion in Cipher2 recovered image is slightly noticeable and in Cipher3 are a little bit more prominent.

• V.    Conclusions

The provided benchmark has discussed a wealth of cryptographic evaluation and performance parameters. These parameters are implemented to evaluate a block cipher, a compression tolerant and a chaos-based encryption schemes. The result of evaluation has demonstrated that block based cipher (AES) is good for cryptographic security as far as the communication channel is free of any distortion and image is not needed to be compressed. Compression tolerant encryption scheme has little security and can be used only in noisy channels or to achieve greater compression at the cost of security. Chaos-based scheme is proven to be a cipher of choice as it has high cryptographic security and demonstrated performance along with some tolerance to tempering, compression or noise. The proposed cryptographic evaluation benchmark can be applied to any image encryption scheme to quantize its security and performance.