A case analysis on different registration methods on multi-modal brain images

Published Online August 2018 in MECS DOI: 10.5815/ijmecs.2018.08.05

Medical imaging [1] is currently at the heart of the device allowing the practitioner to establish a diagnosis or to plan a therapy. The technological advances of the twentieth century have indeed given rise to numerous imaging modalities, which allow an ever more precise vision of the patient's anatomy. In parallel with these advances, the need to analyse the images resulting from these modalities has increased because the volumes of data to be processed are very important. In the absence of efficient automatic analysis tools, the exploitation of data is often done manually.

Image registration [2] plays a very important role in the analysis and interpretation of these data. It allows, as part of the diagnosis, to match images from several imaging modalities, to follow the treatment of a patient over time or to perform inter-patient analyses. It also allows, as part of the conduct of interventional gestures guided by the image, to integrate in the same space information from images acquired in pre- and perioperative situations. The use of registration techniques has been made accessible by recent advances in computer technology, and these techniques now allow the combination of information from different imagers. Nevertheless, the need for effective registration methods is still important today.

For three decades, medical imaging has experienced a very important development related to technological advances in the context of diagnostic assistance or therapy assistance. Today, there are a multitude of medical imaging modalities (conventional radiology, CT scans [3], Magnetic Resonance Imaging (MRI) [4], ultrasonography, scintigraphy, single photon emission tomography (SPECT) [5], emission tomography Positons (PET) [6], etc.), each providing specific and complementary information. These images, which can be two- or three-dimensional in nature and to which the temporal component can be added, represent a mass of very important data to be analyzed. However, these data are still often exploited manually, because of the lack of effective semi-automatic or automatic analysis tools.

Image registration plays a central role in the exploitation and interpretation of these images. Indeed, it makes it possible to compare or even merge the data from different imaging modalities or different patients for a given examination, but also patient monitoring or interpatient analysis. There has been growing interest in this area in recent years. We can see two explanations: first, medical imaging acquisition modalities having diversified, it is interesting to combine these images to extract more information. Then, advances in computing now make possible calculations unthinkable just a few years ago.

The objective of this state of the art is not to exhaustively list all the registration methods available today. We will work instead to define the essential problem of image registration, a problem that is close to motion estimation. For the sake of brevity, we will gradually reduce the range of methods available to focus on those corresponding to our subject of study, namely iconic registration methods (i.e. without prior segmentation) based on mutual information.

• II.    Clinical Motivations

In a few words, image registration consists in deforming a so-called floating image by a geometric (or spatial) transformation in order to perfectly match it to another, referred to as a reference. Under this simple principle, there are many methods, with different clinical purposes. To better understand the issues of registration, we will begin by giving an overview of possible medical applications.

• A.    Unimodal Registration

It is the simplest case [7]. Here, the images come from the same patient, taken with the same imaging modality, but at different times. The uses that can be made of these images include:

• •    The control of surgical operations: a comparison of the pre- and postoperative images makes it possible to verify that the surgery has achieved the desired result (complete removal of a tumor, for example).

• •    Patient follow-up: images have been acquired over different periods, and are compared with each other to judge the evolution of the pathology or to report on the effectiveness of a treatment.

• •    Cardiac motion estimation: cardiac imaging makes it possible to evaluate cardiac function from a morphological, dynamic and / or functional point of view. Typically, two- or threedimensional CT scans (CT, MRI and ultrasound) are acquired at different instants of the cardiac cycle. The purpose of the recalculation is, here, to estimate the movement of the heart from these image sequences.

• •    Respiratory motion compensation:   When

acquiring medical images, the patient's breathing movement can induce artifacts in the images or significant differences between images taken at different times. The registration can thus be used to compensate for this respiratory movement [8].

• B.    Multimodal Registration

This approach is more complex since it involves matching images that may be of different natures. Typical applications are [9]:

• •    Data fusion: it results from the combination of several imaging modalities [10]. Each imaging modality has its own characteristics, and provides different information on the pathology or organ considered. The imaging modalities can be broken down into two major complementary and specific families:

• •    Anatomical imaging (conventional radiology, CT or CT scan, MRI, ultrasound, etc.).

• •    Functional imaging (scintigraphy, PET, SPECT, Doppler ultrasound, functional MRI, diffusion MRI, etc.).

Also, it can sometimes be interesting to merge these different information to establish a diagnosis. The data fusion will therefore consist in the recalibration of images of different modalities. This is a booming field, thanks in particular to the technological advances that make it possible to process ever larger amounts of data. The purpose is obviously to provide a more precise diagnosis, since it is based on several types of complementary imaging.

• •    Intervention planning:  Thanks to a better

knowledge of the internal anatomy of a patient, doctors can establish a better diagnosis and thus better plan their intervention. Indeed, the organs for example may be of different sizes and shapes according to the patients. By pre-operative image analysis, doctors have access to an accurate anatomical description of the target, organs at risk near the target or risks related to the insertion of surgical instruments. It is important that each of these descriptions is accurate, and the combination of information from different imaging modalities improves the final decision.

• 1)    Multi patient Mono- or Multimodal Registration

Many studies point to the possibility of comparing data from multiple patients. This makes it possible, for example, to detect pathologies by comparison with a group of healthy individuals. Generally, the chosen solution consists of deforming individual images to make them correspond to a standard atlas. For example, in functional brain imaging, the creation of a digital atlas involves averaging images of the same modality from several healthy patients (this implies a first inter-patient registration step). A map, or model, of the functional anatomy of the human brain is thus obtained. By recalibrating the image of a patient's brain on this atlas, it is possible to locate the area of the injured brain. The use of digital atlases concerns many applications, among which we can notably quote:

• •    Diagnostic assistance, by comparing an individual to a population "on the ground" represented by an atlas.

• •    The comparison of two groups of individuals between them.

• •    The provision of high level information. In fact, atlases can be used as a source of information for operations such as segmentation, registration, reconstruction, follow-up of lesions over time, etc.

• 2)    LTSI Registration and Problem Positioning

These few examples allow us to glimpse the very important place occupied by photography in the analysis of medical images. In the Signal and Image Processing Laboratory, there are many problems with the registration. Here we give some examples to situate our work.

First, there is work on estimating cardiac motion from three-dimensional image sequences. This estimate is a key issue in the detection of heart disease, and has benefited from advances in dynamic imaging, including the development of three-dimensional ultrasound and multi-array scanner. In this context, rescaling methods dedicated to 3D scanner volumes have been proposed [11].

Still in the field of cardiac imaging, cardiac resynchronization therapy, a difficult intervention procedure, can be optimized by precise identification of left ventricular (LV) [12] stimulation sites, based on anatomical and electrical information, respectively multiband scanner imaging and Electro-Anatomical Cartography (EAC) [13]. In order to represent these data in the same environment, a two-step information fusion method is proposed:

• 1.    Rigid registration of surfaces.

• 2.    3D surface fusion and electrical mapping.

In the first step, two 3D VG surfaces obtained from EAC and segmented scanner images are automatically or semi-automatically recalibrated. In the second step, electrical activation times (AEDs) at each endocardial point are estimated from the EAC. Finally, a graphical interface makes it possible to visualize the AEDs on the VG. Recent work [14,  15] proposes methods of information registration / fusion in this application context.

In the treatment of prostate cancer by image-guided radiotherapy, non-rigid registration also plays an important role in the laboratory. The motivations for the use of the registration are multiple. First, the prediction of toxicity is a fundamental issue, because it allows better control of the radiation received by the patient. In this context, the development of a statistical model of toxicity would make it possible to highlight relationships between the dose delivered and the occurrence of toxicity. The construction of this model involves the development of an atlas, built by inter-patient registration, allowing dose mapping on a model derived from this atlas [16]. On the other hand, when one tries to make a calculation of the cumulative dose received during treatment, it is interesting to be able to follow the movements and the deformation of the organs throughout this treatment, to know which dose of radiation is actually received by the patient. This is a great help in planning radiotherapy sessions. In this context, registration methods have already been successfully applied [17, 18].

Whatever the clinical purpose, the methods of registration of medical images reveal common issues. Often, the constraints imposed by the tissues or organs observed require the taking into account of complex and non-rigid deformations. This is particularly the case in the examples mentioned above. Moreover, the volumes of data to be analyzed, by the progress of imagers, are always more important. It is therefore necessary to have effective registration methods to process all these images in a minimum of time, the purpose being a rapid diagnosis.

• III.    Recalibration: A Problem of Parametric Estimation of Motion

The registration may, first and foremost, be seen as a problem of motion estimation in a sequence of images, a fundamental research theme in image processing. The fields of application of motion estimation range from video compression to the interpretation of satellite images by the way, and this is our subject in this work, by the characterization of dynamic organs. In the literature, there are two main types of techniques: nonparametric techniques and parametric techniques. There are three main types of non-parametric motion estimation methods:

• A.    Differential Methods

They aim at estimating the optical flux between two images from the estimation of spatio-temporal gradients of the intensity in each of the pixels of the image. They are widely used in image processing since the original article by Horn and Schunk [19]. These methods are generally used to measure small displacements, and make the assumption of a conservation of the intensity between the images.

• B.    Block Matching Methods

Their principle is to cut a reference image into blocks of pixels or voxels. The goal is then to try to find in the next image, for each of the initial blocks, the most resembling block. The accepted hypothesis is that the movement between two images is locally translational. These methods are widely used, especially for image or video compression (MPEG) [20, 21, 22, and 23].

• C.    Statistical Methods

Among the statistical methods, the Markovian or Bayesian methods are the most used. They are based on a probabilistic formulation of the field of motion. The considered field is seen as a particular realization of a random field. The most common formulation is based on the Maximum-a-Posteriori (MAP) estimator [24].

We will not present in detail the non-standard methods. Parametric, since this is not the subject of this thesis. Indeed, the registration assumes a certain parametric model of the movement or displacement, since it is based on the estimation of the parameters of a transformation modeling the field of motion. The rest of this document is therefore interested in parametric motion estimation.

• IV.    Classification of Registration Methods

Basically, the registration of input images requires the selection of the feature space, a similarity measure or alignment quality, a transformation type and a search strategy. A great number of medical image registration methodologies have been presented, and several criteria have been proposed to classify them [25] classified the registration methodologies by the data dimensionality (1D, 2D, 3D, 4D), source of the image features used to make the registration (intrinsic or extrinsic properties of patients), transformation domain (local or global), transformation elasticity (rigid, affine, projective or curved), tightness of property coupling (interpolating or approximating), parameter determination (direct or search-oriented), and interaction (interactive, semiautomatic or automatic). The frame is here always the registration in general. Other states of the art focus specifically on the registration of medical images. This is notably the case of [26], which lists more than 300 references and defines a new classification of registration methods based on 9 criteria (size of the images, nature of the registration, nature of the transformation, processing sector, etc.).

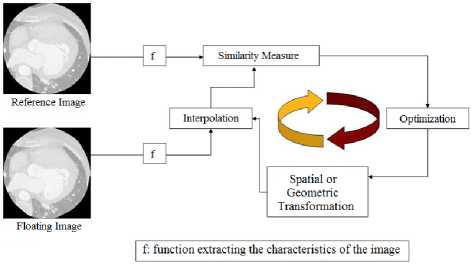
Fig.1. Principle of the registration [25]

Т = arg ^m^ S(f (x(^(v)) ,f((x(²\T(a)))   (1)

Where the selected criteria appear:

• - x⁽¹⁾(iO and x⁽²⁾(i0 are respectively the reference image and the floating image.

  - f is the function extracting the characteristics of the image. Two big classes’ different methods. On the one hand, we find those that use all the image information (iconic methods), on the other those that use the result of a previous segmentation step (geometric methods). We will situate our work on the side of iconic approaches.

  - S represents the similarity measure. This depends on the attributes of the image used, and we will explain why we have turned to mutual information. We will rely in particular on [27] which proposes a state of the art of the registration of medical images based on this one.

  - T symbolizes an element of the space of possible transformations, or model of deformation. The first approaches consider rigid or affine transformations. However, in the context of this thesis, we are interested in the registration of elastic members for which a nonrigid model is essential. Such a model offers more degrees of freedom (DF) vis-à-vis the desired transformation, allowing the estimation of a more complex transformation but closer to reality. The article [28] will support our demonstration.

  - arg ^m^.ⁿ induces the optimization strategy. The volume of data to be processed being generally very important, it seems necessary to choose the algorithm judiciously optimization. As part of our work, a study conducted in [29] reinforced our choices that we will explain later.

This presentation, although general, will gradually move towards the decisions we made during this thesis work. First of all, to successfully complete the registration of two images, one must first choose the information that will be extracted from these images. Three main approaches are then possible:

• 1.    The first relies on geometric primitives extracted from the image, such as points, lines or characteristic surfaces. These methods are therefore commonly called geometric methods [30, 31].

• 2.    The second exploits all the raw information contained in the image (without prior segmentation), namely the gray levels. We are talking about iconic methods [32].

• 3.    The third finally combines the characteristics of the two previous approaches. These methods are grouped under the name of mixed methods [33].

These 3 approaches each have their own interests and limitations. The geometric methods will be intentionally presented in a succinct way, the objective being above all to give a point of view to the reader and to be able to compare the advantages and the limits of each one. On the other hand, we will explain more precisely the iconic methods that fall within the scope of our study.

• A.    Geometric Approaches

In this type of approach, geometric characteristics are extracted from the two images to be recalibrated, then the actual registration will consist in finding the transformation between these characteristics resulting from the two images. This geometric transformation is the one that minimizes the distance between paired features. This is historically the first method to have been used, and this may be explained by the fact that the process of geometric registration resembles what is done naturally by human visual perception: we look in the images studied for remarkable points and common lines or surfaces that we are trying to match. The primitives used can be classified according to their nature: geometric primitives (segments or planes), topological primitives (connected components, cavities, surfaces or intersections of surfaces), morphological primitives (skeleton or related envelope), or differential primitives (ridge lines, discontinuities). The geometric attributes can then be external markers (like the points of a stereotaxic frame visible by the different imagers for example), points, contours or surfaces.

The major advantage is a limited processing time. Indeed, considering only a compact representation of the image, the computing load is reduced accordingly. In addition, extracted primitives are very informative since they are based on high-level features of the image related to the object of interest.

However, the majority of the approaches are based on a manual selection, or on a semi-automatic detection of the bitters (or geometric primitives) common to the two images, which imposes a pre-treatment of the data to extract these points, lines or surfaces interest. On rigid structures such as bones, the task is relatively simple since the identifiable bitters will be stable on the different images. On the other hand, the problem is much more complex on soft structures such as the heart, since the selection of bitters (endocardial surface, for example) will require prior segmentation. The quality of this initial segmentation will then depend on the robustness of the registration. Moreover, to obtain an interesting result in non-rigid registration, the number of geometric characteristics will have to be important, the quality of the interpolation of the images between these characteristics depending directly on their number.

We will not dwell on the distances used to match the geometric primitives. Nevertheless we can give some axes according to the primitives used:

For points (such as Moravec points or Laplacian zero crossings), the conventionally used distance is a simple Euclidean norm. It leads, in the context of rigid and affine registration, to an analytical solution by the method [34].

For curves (more precisely the orientation and direction of these curves) or surfaces generally obtained by deformable or level-set models, several approaches are possible: the ICP (Iterative Closest Point) algorithm [35], distance maps and interpolation [36]/ radial function approximation (RBF for Radial Basis Function) [37]. For the latter approach, [38] use Thin Plate Splines (TPS) as a radial function, while [39] serves as elastic splines or [40] as volume splines.

• B.    Iconic Approaches

The iconic methods are based on the estimation of a deformation that maximizes an energy function reflecting the similarity between the images. The similarity measure operates here generally on the totality of the raw data of

Table 1. Advantages and disadvantages of different approaches to registration of medical images

	Geometric Method	Iconic Method
Advantages	•   Reduced processing time. •   Very informative primitives.	•    Suitable      for multimodal registration. •   No preprocessing required. •    Automatic method.
Disadvantages	•   Manual selection     or semi-manual primitives. •    Usually reserved     for unimodal registration. •    Preprocessing necessary (segmentation).	•    Uninformative primitives (from low level). •    Important treatment time.

the images (grayscale), or more rarely on a representation of these gray levels: thus, [41] apply a Fourier transform on the images for working in the frequency domain using phase information, while a decomposition of the wavelet image is used by [43]. Direct grayscale methods appeared by [43] in the rigid and unimodal framework. With the progress of medical imaging has subsequently emerged the problem of multimodal registration which is defined as the comparison of images from different modalities. In this context, geometric approaches have shown their limitations, in particular by the difficulty of extracting equivalent primitives in images of different natures. Indeed, in the case of geometric approaches, the quality of the estimation of the desired transformation is totally conditioned by the segmentation of the images (detection of geometric primitives). The iconic methods have gradually supplanted them in multimodal registration. The work of [44] has led to a significant advance in this direction with the introduction of the concept of a joint histogram, which has become a very effective tool for reregistration in the iconic framework. Mutual information was then used [45] and its success never faltered thereafter. We will come back in detail later on these similarity measures used in iconic registration.

The iconic approaches have the particularity of not requiring pre-treatment to reduce the mass of data, as is the case with geometric approaches. They are considered the most flexible registration methods, since they use all the image information during the registration process. Another advantage of the iconic methods is their automatic character: they do not require manual selection or segmentation, often delicate, of geometric primitives common to both images. However, they still have some disadvantages. Firstly, the characteristics extracted from the image (in general the gray levels) are not very informative compared to the geometric primitives. Secondly, the processing time is generally higher than that of the iconic methods, since no pre-treatment reduces the initial mass of available data. Table 1 summarizes the main advantages and disadvantages of geometric and iconic methods. The mixed approach, which follows, has not been included in this table since its purpose is precisely to overcome problems related to x two previous approaches, to keep only the advantages.

• C.    Mixed Approach

Mixed approaches combine several types of features extracted from images to be recalibrated. The goal is to improve the robustness of the registration by combining the advantages related to the characteristics used. Three cases are envisaged:

• •    The combination of geometric primitives of different nature. It can refer for example to [46] for the combination of curves and surfaces.

• •    The combination of different information from the gray levels, as is the case in [47] where the gradient of the image and the information of the gray levels are used together [48], for their part, construct an attribute vector for each voxel in the image. This vector contains both the intensity of the voxel in question, the invariant geometric moment characteristic of the vicinity of the voxel, and information resulting from the segmentation into 3 classes of the image.

• •    The combination of geometric and iconic approaches. In this case, geometric primitives are usually used to constrain iconic primitives.

In the literature, studies are specifically concerned with the comparison between iconic and geometric methods for the registration of medical images [49] or more specifically the registration of brain images  [50], showing the superiority of iconic approaches to geometry. There is also a study published by many researchers [51] that compares a dozen methods of registration and advocates the use of iconic methods in the context of multimodal registration of medical images. This is partly what motivated our initial choice to work on iconic methods. Mixed  approaches  combining different information from gray levels can nevertheless be considered in future work, the information provided by the gradient of the images being for example interesting in the context of our method.

• V.    Similarity Measurements in Iconic Registration

Iconic registration is based on the local comparison of intensities. As a result, iconic similarity measures operate directly on the gray levels of images, making use of all available information. These measurements make an assumption on the relationship linking the gray levels of the two images to be recalibrated. In general, the nature of this relationship allows a classification of the different similarity measures, as we will see in the following. Also, the choice of the criterion of similarity is guided by the nature of the images to be recalibrated. However, it is also necessary to consider the numerical complexity of this or that measure. A measure allowing to apprehend very general relations between images will often be more expensive and more difficult to optimize. Many similarity measures have been proposed in the literature, and some articles even propose a comparative study of these criteria [52]. Overall similarity measures are usually calculated from a set of intensity pairs taken from the reference image and the floating image. Before explaining in more detail these measures, a probabilistic framework is explained below.

• A.    Probabilistic Model of Images

To evoke the similarity measures in iconic registration, it is interesting, if not necessary to formalize the problem by adopting a probabilistic model of images. Firstly, in the following, the intensity of each pixel / voxel of the reference image (respectively floating) will be considered as an achievement of a Random Variable (RV) denoted x⁽¹⁾ (resp (х ( ² ) )) with value in the set D⁽¹⁾ of the gray levels (respectively in O⁽²⁾. The random draw of x⁽¹⁾ (resp (x⁽²⁾)) representing this intensity of the pixel v of the reference image (respectively floating) will then be denoted x⁽¹⁾(v) (resp (x ( ² ) )(v)). Let x = (x⁽¹⁾,x⁽²⁾)^T (T for transposed) be the random vector composed of the two УЛ , x⁽¹⁾ cm.d x⁽²⁾. We will assume in the following that the densities of probability.

The marginal eigenvalues of x⁽¹⁾ and x⁽²⁾ , denoted P x(1) and P x( ₂ ) the joint probability density of x, denoted p_x , are defined. Note that such a probabilistic model of images, commonly used in the literature [53], assumes a certain stationarity in terms of the probability law from one pixel to another of the image. We give in the following some widely used similarity criteria measuring the dependencies that exist between the intensities of the images to be recalibrated. We use from present and in all that follows the formalism that we have adopted to establish the links between these measures.

• B.    Intensity Conservation

The first iconic measurements that appeared in the registration of medical images considered ideal the situation where the images are identical to a near spatial transformation. Indeed, these first measurements were based on the assumption of conservation of the photometric information (identical gray levels in the two images to be repositioned). Of course, this assumption proves to be inaccurate in almost all the practical situations encountered, but as long as the images remain relatively similar (as may be the case for unimodal images for example), this approximation may be sufficient. Thus, [54] have theoretically justified the use of the sum of squared differences (SDC), or L2 standard of the difference, when the images are identical to a spatial transformation and to an Additive White Gaussian Noise. This measure is still widely used as a likelihood criterion in the context of intra-subject unimodal registration, although the noise of medical images is rarely Gaussian. This measurement normalized by the number N of pixels can be interpreted as an estimate of the mean squared error (MSE) between the two images:

—SDC ® E [(x⁽¹⁾ - x⁽²⁾) 2 ]

= ^(u¹¹ - u^№)²p_x(u)d.u         (2)

Where E [.] designates the operator of the mathematical expectation. We can include the sum of the differences in absolute value (SDA), or L1 standard, which can also be interpreted as an estimated of a statistical quantity:

1 SDC ® E[|x⁽¹⁾ - x⁽²⁾|] = $_r2|u⁽¹⁾ - u⁽²⁾|p_x(u)du (3)

More particularly, the SDC and SDA measurements are defined by:

SDC = Z pixeisy (x^v) - x⁽²⁾⁽v))     (4)

SDA = ^pixels v |^⁽¹⁾(v) - x⁽²⁾⁽v)|        (5)

Other criteria have also had some success. For example, we can cite the number of sign changes in the difference image or the intensity pattern, which could be translated as "intensity patterns", which operates on the difference of images, revealing structures or motifs of interest.

But the limitations of these measurements quickly appeared, since the initial hypothesis (conservation of the intensity in the images to be recalibrated) is too strong in practice. Indeed, their use is limited to the comparison of unimodal images intrapatient in the study of the evolution of pathologies. But the needs of medicine are diversifying with the emergence of many imaging modalities and the possible combination of information provided by these methods, researchers were then interested in measures making less strong assumptions about the intensity of images to reset.

• C.    Linear or Affine Transform

The intensity conservation hypothesis showing its limits (in a unimodal case such as the alignment of MRI images of the same sequence, this hypothesis is for example already no longer satisfied), researchers have tried to model more complex relationships between images. Thus, the next step was to assume a linear or affine dependence between the intensities of the images, which can be expressed by:

x⁽¹⁾ = ax⁽²⁾ + p , (a,P)eR²           (6)

Where α and β are unknown constants. When the parameter β is zero, one speaks of linear dependence between the intensities, if not of affine dependence. The reference criterion, in the linear case, is the standardized cross-correlation coefficient (ICC) which is given by:

ICC =

/■:|x ¹ ' ²

Z[x⁽¹ ) ]E[x²

f_R 2 u⁽1⁾u⁽2⁾p_x⁽u⁾du

Jf_Ru⁽1⁾p_x⁽1⁾(u ( ¹⁾)d u ⁽¹⁾ ^R ^u(2) P_x⁽2⁾(u ⁽²⁾ ) du(2)²

• D.    Functional Dependence

The functional dependence is even less restrictive than an affine dependence, since one does not presuppose a causal relation linking the two images to be recalibrated. The only hypothesis here is that knowledge of the distribution of gray levels of an image makes it possible to predict perfectly the second. The converse is not necessarily true. Thus, it is envisaged here the possibility of a registration between different modalities, information common to both images, such as anatomical structures, may be sufficient to verify this hypothesis. However, we must first ensure that the two modalities in question provide access to anatomical information fairly close, otherwise the assumption is quickly debatable and too strong once again.

• E.    Statistical Dependence

By considering only a statistical relationship between the images, a further step was taken towards multimodal registration. The notion of statistical dependence being more general than the notion of functional or affine dependence, the measures of this class are those based on the weakest hypotheses. This was made possible by the concept of a joint histogram developed by [55] to estimate the joint probability density p_x of the two images to be readjusted. Author has realized that when two images are incorrectly registered, their joint histogram tends to disperse. Thus, a measurement taking into account the dispersion of the joint histogram makes it possible to recalibrate two images. Rather than using only the p_x joint probability density, researchers turned to information theory, and Shannon's probabilistic framework to propose new measures.

• VI.    Transformation Models

A crucial choice to make before tackling a medical image registration problem is the model of deformation or geometric transformation to take into account. This will define how the floating image x(2) (v) will be distorted to match it better to the reference imagex(1) (v). This choice is generally oriented by three constraints:

• •    The Structures to be Re-calibrated: The deformation model will not be the same depending on the anatomical structures to be recalibrated. To recalibrate bone structures, for example, the deformation model will be different from that used to recalibrate soft structures such as the heart. The deformation of the bones being generally rigid between 2 images, a simple model (rigid or affine) deformation is often sufficient. If

one wants to be interested in the registration of cardiac images on the contrary, the generally nonrigid character of the deformations of the organ must necessarily be taken into account.

• •    Clinical Purpose: An affine deformation model may be sufficient for a measurement of unimodal registration, whereas in the context of a multimodal registration, it will often be necessary to resort to more complex models.

• •    The Degree of Realism of the Model: A model of deformation one is realistic, that is to say that it allows highly non-rigid transformations, more its number of degrees of freedom (DF) is in general important. DFs represent the size of the search space, that is, the number of parameters to find. During the optimization process, each transformation parameter must be identified. It therefore seems obvious that the more complex a model, the more difficult it will be to optimize it in terms of calculation time.

Whatever the deformation model chosen, the transformations can be global, i.e. applied in the same way (i.e. with the same set of parameters) at all points of the image. , or local, the image then being cut into regions having their own transformation. In general, transformations with a small number of DFs (rigid, affine, and projective transformations) are applied globally, whereas non-rigid transformations are applied locally. An illustration of all these transformations is given in Figure 2. In addition, a registration procedure is often initialized by means of a rigid or global affine registration to correct the large deformations or differences inherent in the imaging modalities, and it continues with a local nonrigid registration to capture the deformations more finely. Thus, the final transformation is written:

T(v) = Tsio6ai(v) + T1.oca.l(y)          (8)

This state of the art will again be succinct and oriented towards our problem. Finally, comparative studies of several reference algorithms have been conducted by many researchers [56]. In this latest study, which focuses on the non-rigid registration of MRI brain images, the B-Splines algorithm is one of the most successful at present. This reinforced our choice for this deformation model:

• A.    Rigid Transformations

Rigid transformations take into account only rotations and translations of the image, and thus preserve angles and lengths (isometry). They usually belong to the smallest search space used for registration, since they only contain 3 DF (1 rotation and 2 translations) for 2D or 6 DF images (3 rotations and 3 translations) for volumes of images. These transformations are generally suitable only for unimodal approaches, when for example it is sought to compensate for the difference in positioning of a patient with respect to the sensors without taking into account possible distortions of the imaged tissues. They can also be chosen as a preliminary step before a non-rigid registration. In what follows, we will present the different types of transformations in mathematical form and for three-dimensional images. Thus, the rigid transformation recalling a floating image x(2) (v) on a reference image x(1) (v), i.e. allowing to obtain the following equality:

^v,x(1)(V) = x(2)(MR(v, 1)T) (9)

Where, M_R is a rigid transformation matrix obtained as the matrix product of rotation and translation matrices.

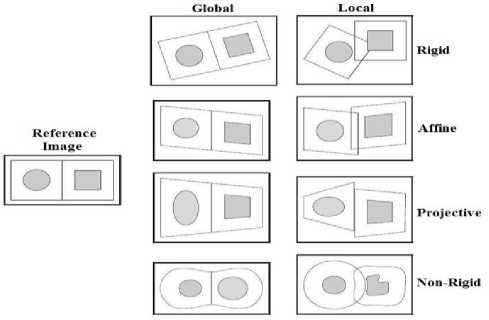
Fig.2 . Representations of the different deformation models [57]

• B.    Affine Transformations

These classes of transformations are used for relatively rigid structure registration, or to initialize a non-rigid registration. This is the second case that interests us. Indeed, we have seen that the affine or rigid transformations are generally applied globally to the image, while the non-rigid transformations that we will present in detail in the following apply locally. This classification is not always exact, and it is necessary to note the interest of the use of piecewise affine transformations in some for inter-subject registration [58]. But in the following, we only consider affine global transformations. It is often interesting to start a procedure of non-rigid registration by a registration considering this type of transformation. This makes it possible to compensate for large deformations due, for example, to the positioning of the patient on the examination table, or simply to the difference between the image modes (correction of the scale factor). To obtain an affine transformation, the scale and shear factors must be added to the rigid model. In 3D, there are 3 scale factors (1 in each direction) and 6 shear coefficients. This brings the number of 3D DFs to 15 (and to 7 in 2D). The transformations are applied matricially according to the equation (9), except that the rigid transformation matrix M_R is replaced by an affine matrix M_A .

Thanks to these two relatively simple deformation models, it is already possible to represent a large number of deformations. However, our initial subject being the iconic registration of organs, and given the non-rigid nature of these deformations, we had to equip ourselves with a more realistic transformation model. It must be able to accurately model the complex deformations of a set of tissues or distortions.

Geometric characteristics inherent to certain acquisition methods. In the following, we present the main models of non-rigid deformation used in iconic registration of medical images, and we will focus on the approach we have selected.

• C.    Non-Rigid Transformations

In contrast to rigid and affine models, non-rigid deformations are applied locally, i.e. the transformation applied at one point may actually be different from that applied to its neighbours. They therefore correspond to the term T_local (v) of the equation (8) and intervene in our method after a first affine registration. The amplitude of the deformations sought is generally weaker and localized. A large number of non-rigid deformation models have been proposed in the registration literature. Among these, we will distinguish between:

• •    Non-Parametric Approaches : In which the transformation is defined in each pixel of the image. These models require the use of a regularization term to constrain the solution, because the deformation model is completely free.

• •    Parametric Approaches: Which are based on polynomial interpolation (usually piecewise) of a deformation field, using a set of Control Points (CPs) placed in the image domain.

These approaches, from which our deformation model is derived, are implicitly constrained by the polynomials used to model the deformation field. Although more expensive than non-parametric approaches, they are generally preferred for multimodal applications. It should be noted that the rigid and affine deformations that we have just present can also be considered as parametric, since they are constrained by the coefficients of transformation matrices M_R and М_д which impose a finite number of DFs.

• 1)    Non-Parametric Approaches

This first type of method considers free transformations, not constrained by a space of small dimension. This approach is defined by the largest possible transformation class, since each voxel in the image has an independent motion vector. However, by this approach, the measure of similarity does not depend on the transformation only via a finite number of points corresponding to the voxels of the reference image x(1)(v). Indeed, two transformations can be different while coinciding on the grid of the image, and we see then that the single measure of similarity is not enough to decide between them. It is then necessary to regularize the problem of optimization by following the theory of the approximation of Tikhonov. This amounts to adding to the measure of similarity a term of regularization independent of the images and which constrains the space of the possible transformations, to restrict it for example to diffeomorphisms. The problem of registration can then be formalized by:

To = argm™ [S(f (x(1)(v)),f ((x(2)(T(v)))) + AR(T)               (10)

Where, S (f (x(1) (v)), f ((x(2) (T (v))))

represents

the measure of similarity, T?(T) is the term of regularization and λ is a scalar which controls the relative influence of the two terms.

It is on the term of regularization that we will bring our attention, because many works were interested in its construction. The regularization of the registration problem is necessary to constrain the space of solutions to consider only fields of deformations "physically acceptable" (a bone structure must remain rigid for example). It is expressed by constraining the deformation by internal forces depending on the behavioural properties of the considered transformations. Here we present the main regularization energies used in the registration of medical images. It should be noted that few of them are used with mutual information as a measure of similarity, which is why we will present them briefly.

Optical Flow: The optical flow method is an optical flow-based registration technique, which is equivalent to the flow equation of incompressible flows in fluid mechanics. This method makes the assumption of intensity invariance between images, it is generally reserved for unimodal registration. Their regularization term comes from the theory of motion estimation, and more specifically from the optical flux, corresponding to the membrane model.

Elastic Model: The elastic physical model considers the floating image as a linear elastic solid and deforms it using forces from the chosen similarity measure. Two forces then oppose: the internal elastic force that opposes the external force of the similarity measure. The floating image is then distorted until both forces reach equilibrium. The linear elasticity hypothesis is valid only for small deformations, so it is difficult to find large transformations thanks to this regularization. This term of regularization, related to the physics of the objects of the registration, is given by the elastic potential of the field of displacement. This potential is governed by the Navier linear elastic partial differential equation:

g1V2u(v) + (A; + (u;)V(VTu(v)) + 6(v) = 0  (11)

Where A ; and g ^ denote the Lame constants that quantify the elastic properties of the model, u(v) represents the displacement field and b (ν) represents the external forces experienced by the material. In our framework, 6(v) represents the force aiming at matching the characteristics common to both images.

Fluid model: The fluid model makes it possible to account for large and localized deformations because it is very flexible. The counterpart to this flexibility is the risk of misalignment, usually because of the growth of one region that has replaced the distortion or displacement. The partial differential equations governing this model are the same as those of the elastic model (equation (11)), except that they affect velocity rather than displacement (Navier-Stokes equations). These methods are expensive in computing time.

• 2)    Parametric Approaches

The parametric approach is called self-constraint because the regularization is done directly thanks to the deformation model. These approaches are parameterized by CPs distributed regularly or irregularly on the reference image. Each of these CPs is associated with a position vector representing the parameters of the CP. The overall transformation is then obtained by extrapolating the transformation outside the CPs by different methods. These approaches have a form of regularization intrinsic to the transformation, due to model used to express the deformation field. This field is modeled by a sum of basic functions P(v) . These functions can have global support, i.e. their influence will extend over the entire image. This is particularly the case for radial-based functions (RBF), thin-plate functions (TPS for Thin Plate Splines) which are a special case of RBFs, but also polynomial functions.

A regularization term can be added to the cost function to penalize undesirable deformations, thus reducing the number of local minima. For non-parametric registration methods, this adapted regularization term is essential to ensure the continuity (and thus the differentiability) of the dense deformation field.

In the following, we will note p_k of the index CP, where к represents the total number of CPs employed for the transformation model. The displacement f^(k^ = (j®), f^, f Z^) ) of p_k entails, following the selected function base, a move on the whole or only part of the domain definition.

The continuous deformation of the image is calculated by interpolating the displacements discrete CPs. As part of the registration process, all the movements of the CPs constitute all f = f^(k) Parameters to be estimated. So there are in these methods d X к parameters to estimate for dimensional images. Moving a point v of the image expresses itself as a linear combination of a displacement term and a function of interpolation whose support remains to be defined:

4>(v,f^(k^ = X keK( _V ) f^(k)P(v) (12)

Where keK(v') a subset of CP that influences the displacement of the point is v and p (v) is the chosen base of functions. Generally, the separability hypothesis is introduced into each dimension of the chosen base, and we therefore have:

P(v) = /?x(v)Py(v)Pz(v) (13)

We see here that the choice of CPs will have an important influence on the type of transformations used. The distribution and the number of CP determines the elasticity of the deformation and the number of DFs. As part of the iconic approach based on B-Splines, CPs are regularly spaced.

Thin Plate Splines (TPS): TPS are so called because the thin plate spline models the shape of a thin, deformed metal plate. GSTs are part of a larger family of splines based on RBFs. They form the radial function most used in image registration, although other functions such as multi-quadratic or Gaussian functions are also quite common. In this approach, the CPs are considered additional parameters of the similarity measure and are repositioned iteratively after being initialized by hand. In addition, each CP belonging to a thin plate has a global influence on the transformation that is to say that if its position is disturbed, all the points of the floating image move with it. This limits the ability of this method to model complex and especially localized deformations. In addition, as the number of CPs increases, the computational cost of moving a single CP also increases. But this approach did not seem to us totally adapted to our problematic, because the transformations that one seeks to characterize are localized and of low amplitude. Also, we are interested in the second large family of polynomial bases used in parametric registration that are the B-Splines.

B-Splines: In contrast to TPS and their overall support, B-Splines have the advantage of having a compact support. Indeed, B-Splines are defined in the vicinity of their CP. Thus, disturbing the position of a CP affects the deformation only in the vicinity of this CP. It then becomes possible to model localized deformations. It is in part the compactness of their support that made the B-Splines successful for re-imaging medical images, etc. Besides the fact that this compactness makes it possible to describe localized transformations, it is also an advantage in terms of computational cost, because the displacement of a CP influences only the neighbourhood of this CP.

• VII.    Optimization Strategy

In the previous section, we saw that a deformation model corresponds to a set of parameters to be estimated. For the affine transformation, these parameters, contained in the transformation matrix M_A, there are 15 in 3D. The number of parameters of the vector ξ of the non-rigid transformation FFD B-Spline is itself variable according to the number of CPs of the deformation grid, but it is often several thousand parameters to estimate. An exhaustive search in the parameter space is then totally unthinkable, because the processing time would be prohibitive. It is therefore necessary to use an optimization method, which will make it possible to find the optimal parameters to answer our registration problem, while avoiding this exhaustive search.

Stochastic optimization methods, which progress towards a global optimum, are not very adapted to our problem because the large number of parameters to optimize makes their use very expensive in computation time. We have therefore turned to deterministic methods, which seek a local optimum. The advantage is a reduced processing cost. But the counterpart is that they do not necessarily converge towards a global optimum, and can remain "locked" in a local optimum. To guard against this, it is necessary to initialize the algorithm sufficiently close to the solution. To achieve this, optimization is carried out in two stages: firstly, the parameters of the affine transformation are estimated in order to recalibrate our images globally. Then, optimization to identify the parameters of the non-rigid transformation is conducted to correct local deformations. The principle remains the same in both cases, so we chose to present a unified approach to both situations. In the following, we will note ц the parameter vector to be estimated. Optimization consists of determining the optimal set of parameters g_o . One of the most popular iterative optimization rules is given by:

H_k+ i = H_k + a_kBd_k,k = 0,1,2 ........ (14)

Where □ is the Hadamard product operator, dk represents the search direction at iteration k, and ak is the gain factor or not. Very often, ak = ak.[1......1]T with ak a scalar gain factor which controls the size / length of the pitch in the selected search direction. These two parameters are chosen so that jUk converges to a minimum of the cost function considered. The configuration of an optimization algorithm based on the rule (14) is thus reduced to the way of calculating these 2 parameters dk and ak.

• VIII.    Evaluation of Accuracy of Registry

Evaluating the accuracy of the record is not a trivial problem, since it is difficult to distinguish between an imprecise record and the physical differences of the images, especially when it is a multimodal record, so different approaches have been proposed in literature [28]:

• A.    Mutual Information (MI)

Construction of the attached histogram consists of counting the occurrences of the value pairs of pixels (I (x), J (T (x))) in the overlap area. In the case of Greyscale images 8 bits, the attached histogram is a matrix P of size 256×256. A cell of this matrix is denoted pi, j with 0 < i < 255 and 0 <  j <  255.

The principle of similarity measures using the attached histogram consists in determining the deviation of the histogram from the diagonal. Mutual information is one of the classic measures using the attached histogram. The definition of this measure is given below:

^а.км  X , Jog\J    (15)

X P t P ]/

• B.    Axes Position Error

Centroid of an object lies on the cross point of its horizontal and vertical axes as shown in figure below:

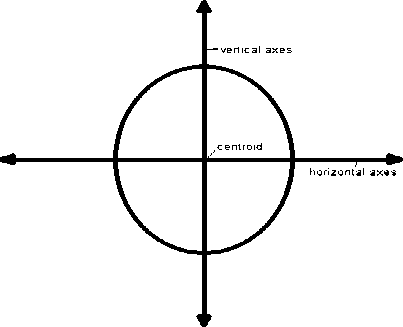
Fig.3. Axes position error [59]

Let’s assume we have two objects having centroid (х 1 ,У 1 ) and (x₂,y₂) and oriented on different angles 6 1 and 6₂ respectively then positional and orientation error of their alignment can be given as below:

Positional Error:

d error = ^(X 2 - X 1) ² + (У 2 - У 1 )²     (16)

Orientation Error:

6 error = 6 2 - 6 1               (17)

To represent these errors in unit quantity, above equations can be written in terms of axes error as shown below:

Horizontal axes position error terror = (У2 —У1) COS(62 — 61)      (18)

Vertical axes position error terror = (X2 — Xi) Sin(62 — 61)       (19)

When h_error and v_error zero than object are will be perfectly aligned.

• C.    Cross-Correlation (CC)

It is a measure of similarity that is calculated from a pair of windows, one of the standard image and another of the candidate. The normalized cross-correlation between two images / and g is given by the equation:

S r [Лr)-E{/(u)Hy(r-u)-ECg)}]

V2 r [r(r)-E{r(u)}] ² V2 r [(r-u)-ECg)l ²

Where r is the coordinate of a window centered on the coordinate u (r,u £ Д²) , E(g) and E(f) are the expected value of g and / in the window where it is being correlated.

Normalized cross-correlation can only very accurately align transposed images, and it turns out to be one of the methods most used in the literature. The normalized cross-correlation between an image and a region of this.

• IX.    Conclusion

This state of the art has allowed us to present the issues raised and the techniques used to re-image medical images by highlighting at each step the choices made in this work. As the notion covers a fairly large field of methods, we deliberately focused during the chapter on our subject of interest, i.e. the non-rigid registration of multimodal images. To do this, we presented each of the components of a registration method (features from images, similarity measure, deformation model, optimization, etc.) while trying to guide the reader towards the choices we made in according to our initial objectives. The aim here was not to be exhaustive, given the number of methods proposed in the literature. Focusing on the components that have interested us in this work, we have seen that iconic methods, especially those using MI as a measure of similarity, are at the moment the most effective ones to answer our problem. The heart of this thesis work on the proposal of a new method of estimating MI, it seemed appropriate to devote the chapter that comes to highlight this statistical measure and the different ways to estimate it. Indeed, MI can be associated with different definitions, methods and approximations. The purpose of this next chapter is to specify the approach that led us to define the MI approximated by a particular function of cumulates of order greater than or equal to two.