A Chaos-based Image Encryption Scheme Using 3D Skew Tent Map and Coupled Map Lattice

With the rapid developments in digital image processing and network communication, electronic publishing and wide-spread dissemination of digital multimedia data have been communicated over the Internet and wireless networks. Therefore it has become urgent to prevent them from leakages. Many applications, such as military image databases, confidential video conference, medical imaging system, online private photograph album, etc. require reliable, fast and robust secure system to store and transmit digital images. The requirements to fulfill the security needs of digital images have led to the development of effective image encryption algorithms. Digital images possess some intrinsic features, such as bulk data capacity, redundancy of data, strong correlation among adjacent pixels, being less sensitive as compared to the text data, etc. As a result, traditional encryption algorithms, such as DES (Data Encryption Standard), RSA [1], are thereby not suitable for practical digital image encryption due to the weakness of low-level efficiency while encrypting images. Fortunately, chaos-based image encryption algorithms have shown their superior performance. Chaos has been introduced to cryptography as its ergodicity, pseudorandomness and sensitivity to initial conditions and control parameters are close to confusion and diffusion in cryptography. These properties make chaotic systems a potential choice for constructing cryptosystems [2-4].

Recently, some chaos-based image encryption algorithms were broken due to their small key spaces and weakly secure encryption mechanism [5,6]. To overcome the drawbacks such as small key space and weak security in chaos-based image encryption algorithms, many researchers turn to find some improved chaos-based cryptosystems with large key space and good diffusion mechanism [7-10]. In this paper, an efficient image encryption scheme based on the ergodicity of 3D tent map and coupled map lattice is proposed. Firstly, one 3D tent map with three control parameters is utilized to generate chaotic orbits applied to permute the pixel positions, then one coupled map lattice is employed to yield two random gray value sequences to change the gray values by bitxor operation so as to strengthen the security. Experimental results have been carried out with detailed analysis to demonstrate that the proposed image encryption scheme possesses large key space to resist brute-force attack and possesses good statistical properties to frustrate statistical analysis attacks. Experiments are also performed to demonstrate the robustness against malicious attacks like cropping, noising, JPEG compression, etc.

The rest of the paper is organized as follows. The 3D skew tent map and its chaotic nature are introduced in Section II. An image encryption scheme consisting of a diffusion process and a permutation process is proposed then in Section III. The performance analysis is presented in Section IV, including the key space analysis, statistic analysis, differential attack, resistance to cipherimage attacks. Experimental results show that the proposed image encryption scheme is secure and robust. Section V concludes the paper.

• II.    3D Skew Tent Mmaps and Its Chaotic Nature

The unimodal skew tent map T 0 : [0 , 1] ^ [0 , 1]

is

given by

^T 0 ⁽ x ) = '

x I a, (1 - x) I (1 - a), if x e [0, a], if x e (a ,1],

where x e [0,1] is the state of the system, and a e (0,1) is the control parameter. It is a noninvertible transformation of the unit interval onto itself. As a = 0.5 , T0 becomes the regular tent map. The transformation is continuous and piecewise linear, with the linear regions [0, a] and [a,1]. Note that the slope of the left branch is 1 / a > 1 and the slope of the right branch is — 1 / (1 — a) < — 1 . For any a e (0,1), the piecewise linear map (1) has Lyapunov exponent —a ln a — (1 — a)ln(1 — a) , which is larger than 0, implying that the map is chaotic. There exist some good dynamical features in skew tent maps. It has been verified that the probability density function p0 (x) of the skew tent map is the same as the regular tent map [11], that is, 1, if x e (0,1),

^ 0 ,    otherwise .

P o^{( x} ) = *

In this paper, we extend the unimodal skew tent map (1) to 3D skew tent map T : [0 - 1]³ ^ [0 , 1]³ by the following way.

(x -y - z)),       (x - У - z) e [0- a)x [0- P)x [0- Y )- a P Y

(x - y - 1—z)-      (x - У - z) e [0- a) x [0- P) x [ y, 1], a P 1 — Y

(x - T^y - z)-      (x - У - z) e [0- a) x [ P-1] x [0- y )- a 1 — P Y

( x - 1-^ - 1— z )-    ( x - У - z ) e [0- a ) x [ P -1] x [ y - 1],

, a ^{1 — P 1 —} Y

T ⁽ x ^- y ^- z ) = f     1 _

• (-^ - y - -),     ( x - У - z ) e [ a -1] x [0- P ) x [0- y )

• 1    — a P Y

(1- x - y - 1— z )-    ( x - У - z ) e [ a -1] x [0- P ) x [ y , 1],

• 1    — a P 1 — Y

(1- x - 1-4 - z )-    ( x - У - z ) e [ a -1] x [ P -1] x [0- y )

• 1    — a 1 — P Y

• (f—x - 14 - ')- (x - У - z) e[a-1]x[P-1]x[Y-1]. (2) 1 — a 1 — P 1 — Y

where , a , P , y e (0 , 1) are the control parameters.

It is easy to show that the three Lyapunov exponents of (2) are (see [12])

Xx = a ln(—) + (1 — a) ln(—-—), a1

• X , = P ln(l) + (1 — P )ln(-l-) ,

P1

Xz = yln(1)+ (1 — y)ln( —))• y

It is obvious that X _x - X _y - X z are all positive, implying that the 3D skew tent map is chaotic on [0 - 1]³ . A typical orbit of ( x ₀ - У ₀ - z 0 ) derived from the dynamical system is {( x_k , У к , z k ) = T k ( x о , y о , z o ) , к = 0 , 1 , l } , which is shown in Fig. 1 for a = 0 . 13 - P = 0 . 3 - y = 0 . 7 , x ₀ = 0 . 6 , y ₀ = 0 . 2 , z ₀ = 0 . 4 . The plotting orbit points fill [0 - 1] 3 as long as the orbit is long enough, which indicates that the system is chaotic visually. The control parameters a , P- y and the initial condition x ₀ , У ₀ , z ₀ can be regarded as cipher keys as the map is used to design image encryption schemes.

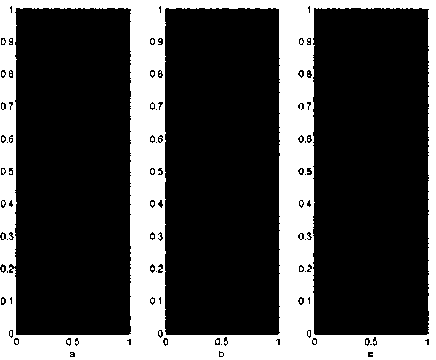
Figure 1. Orbit derived from the considered 3D skew tent map with a = 0.13, P = 0.3, y = 0.7,x0 = 0.6,уo = 0.2, z0 = 0.4 . (a), (b), (c) are the xy , xz , yz -projections of the derived orbit respectively.

• III. The Proposed Image Encryption Scheme

We propose an image encryption scheme consisting of two processes: diffusion of pixel gray values and permutation of pixel positions. In the diffusion process, the coupled map lattice system is utilized to generate pseudo-random gray value sequences, then bitxor operation and mod operation are performed to change the pixel gray values so that the histogram of the cipherimage is significantly different from that of the plainimage, therefore enhancing the resistance to statistical attack and differential attack greatly. The opponent can not find any useful clues between the plain-image and the cipher-image and so can not break the cryptosystem even after they have spent a lot of time and effort. In the permutation process, the 3D skew tent map is utilized to realize the shuffling of pixel positions.

• A.    Diffusion of pixel gray values

Let the processed image is of height H and width W and let HW = H x W . The following coupled map lattice is utilized to generate pseudo-random gray value sequences [13].

У 1 ⁽ n + 1) = 0 ^— £ ) f ⁽ У 1 ⁽ n)) + e f ⁽ y 2 ⁽ n ^{)) -}         (3)

У 2(n +1) = 0 — e) f(У 2(n)) + e f(У1(n))- n = 0-1.L where e e (0,1) is the coupling intensity, f (x) is the well-known logistic map f (x) = Xx(1 — x), x e (0,1), X e (3.5699456,4].

The coupled map lattice system (3) has two positive Lyaponuv exponents as £ = 0 . 99 [13]. Therefore the coupled map lattice system is chaotic. The diffusion process of pixel gray values is outlined as follows.

Step 1. Set the values of the control parameter X for the logistic map and the initial conditions , 1 (0) - y ₂(0) for the coupled map lattice system.

Step 2. Iterate the coupled map lattice system HW times to get two sequences {_ V 1 ( k ) , y 2 (k ), k = 1, l , HW } . Let

• Y 1 ( k ) = floor ( y i ( k ) x 256) ,

Y2 (k) = floor(y2 (k) x 256), k = 1,2, l , HW, where floor(x) rounds x to the nearest integer towards minus infinity. The two sequences Y1, Y2 are then applied to obtain another pseudo-random gray value sequence ф( k), k = 1, 2,l, HW  by the bitxor operation © : ф = Y1 © Y,.

Step 3. The following diffusion function is utilized to achieve the pixel gray value diffusion.

C ( k ) = ф ( k ) © {( P ( k ) + ф ( k ))mod 256}

P (k) = {ф( k) © C (k) © C (k -1) - ф( k )}mod 256, k = 1, 2,l, HW.

Step 4. Reshape P ( k ) , k = 1 , 2 , l , HW to be a matrix Q with height H and width W . Q is the resulted image.

• B.    Permutation of pixel positions

We pile up the gray value matrix Q yielded in the diffusion process to one 3D matrix R with size 1 1 x 1 2 x 1 3 such that HW = 1 1 x l 2 x l 3 + l 4 where Ц ( i = 1 , l , 4) are non-negative integer numbers. If 1 ₄ is not zero, then put the remainder l ₄ pixel gray values into a vector R 1 for the use later.

Step 1. Set the values of a, 0, у, X ₀ , y ₀ , z ₀ . Iterate the 3D skew tent map for HW times to yield three sequences { X n , y n , z n , n = 1 , 2 , l , HW } , then quantize them by

X ( n ) = ceil ( x n x 1 1 ) , Y ( n ) = ceil ( y n x 1 2 ) ,

Z(n) = ceil(zn x 13), n = 1, 2,l, HW where ceil(x) rounds x to the nearest integer towards infinity.

Step 2. Due to the restriction of iteration times, the coordinates ( X ( n ) , Y ( n ) , Z ( n )) , n = 1 , 2 , l , HW may not fill the cube sized l 1 x 1 2 x 1 3 . Find the coordinates which are not ergodic and rearrange them after ( X ( n ) , Y ( n ) , Z ( n )) , we finally obtain one 2D coordinate matrix C with size l 1 1 2 1 3 x 3 .

Step 3. The yielded matrix C is then employed to shuffle the 3D matrix R

R 2( i ) = R ( C ( i , 1) , C ( i , 2) , C ( i , 3)) , i = 1 , 2 , l , l 1 1 ₂ 1 3 .

Set the remainder vector R 1 after R 2 to form a vector with length HW , which is reshaped to be the final cipher-image S with height H and width W . The permutation process is completed.

(b)

Figure 2. The encryption results. (a) plain-image, (b) cipher-image

We choose the plain image Lena sized 256 x 256 .

Fig. 2 shows the encryption results. The cipher keys are

X = 4 . 0 , y 1 (1) = 0 . 6 , y 2 (1) = 0 . 3 , a = 0 . 2 , x 0 = 0 . 4 , в = 0 . 7 , y 0 = 0 . 44 , у = 0 . 56 , z ₀ = 0 . 23 , n = 43 , m = 34 , 1 = 33 .

• IV. Performance analysis

• A.    Key space analysis

  Since the permutation process is irrelevant to the diffusion process, the key space consists of the cipher keys in both processes. In the permutation process, the control parameters a, в, Y , the initial conditions X о , y о , z о and 1 1 , 1 ₂ , 1 3 form the cipher keys. The cipher keys in the diffusion process are X, y 1(1) , y 2(1) . According to the IEEE floating-point standard, the computational precision of the 64-bit double precision number is 2 ⁵² . Therefore the total number of different values which can be used as a is 2 52 , so are the numbers for в, Y, X ₀ , y ₀ , z ₀ , X, y 1(1) , y 2(1) . The key space is (2 52 ) 9 = 2⁴⁶⁸ even without considering 1 1 , 1 2 , 1 3 . Such a large key space can efficiently prevent opponent’s brute-force attack.

• B.    Statistical analysis

Passing the statistical analysis on cipher image is of crucial importance for a cryptosystem. Indeed, an ideal cryptosystem should be robust against any statistical attack. In order to prove the security of the proposed encryption scheme, the following statistical tests are performed.

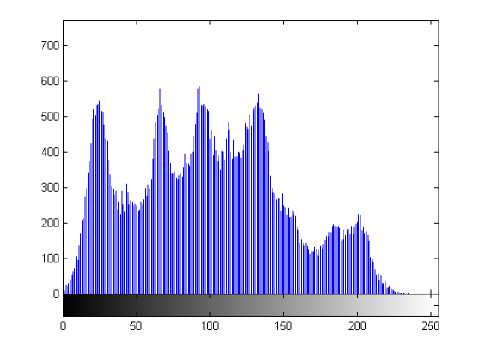
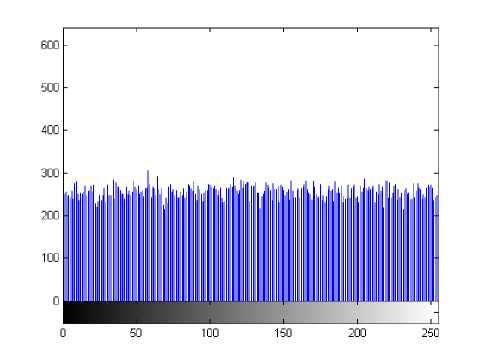
• (i)    Histogram. Encrypt the image Lena with one round, and then plot the histograms of plain-image and cipherimage as shown in Fig. 3, respectively. Fig. 3(b) shows that the histogram of the cipher-image is fairly uniform and significantly different from the histogram of the plain-image and hence it does not provide any useful information for the opponents to perform any statistical analysis attack on the encrypted image.

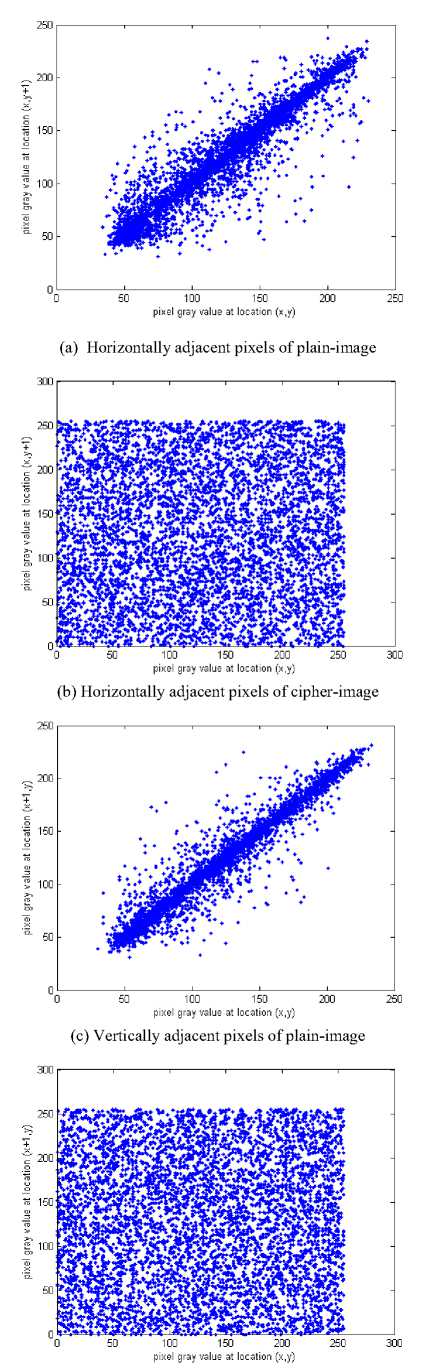
(ii)The correlations of adjacent pixels. To test the correlations between two adjacent pixels, the following performances are carried out. First, we select 6000 pairs of two horizontally (vertically, diagonally) adjacent pixels randomly from an image and then calculate the correlation coefficients of the selected pairs using the following formulae:

Cr =    cov ⁽ x , y )

D ( x ) D ( y )

T cov(x, y) = T ^(x - E(x))(yt - E(y)), i=1

TT

E ⁽ x ) = t X x i, D ⁽ x ) = t X ⁽ X - E ⁽ x ⁾⁾² , i = 1                             i = 1

where X , y are the grey-scale values of two adjacent pixels in the image and T is the total pairs of pixels randomly selected from the image. The correlations of two adjacent pixels in the plain-image and in the cipherimage are shown in the Table 1. The correlation distribution of two horizontally adjacent pixels in the plain-image and that in the cipher-image are shown in Fig. 4.

(a)

(b)

Figure 3. The histograms of the plain-image and the cipher-image. (a) the plain-image, (b) the cipher-image.

Table 1. Correlation coefficients of two adjacent pixels in two images

	Plain-image	Cipher-image
Horizontal	0.9725	0.0116
Vertical	0.94073	0.0038
Diagonal	0.9235	0.0239

(d) Vertically adjacent pixels of cipher-image

Figure 4. The correlation distributions of adjacent pixels.

• (iii)    Information entropy analysis. The entropy is the most outstanding feature of randomness. The entropy H ( m ) of a message source m can be measured by

L - 1

^{H (} m ) = - У P ⁽ mi ^)log⁽ P ⁽ m)) i = 0

where L is the total number of symbols m , p ( m ) represents the probability of occurrence of symbol m and log denotes the base 2 logarithm so that the entropy is expressed in bits. For a random source emitting 256 symbols, its entropy is H ( m ) = 8 bits. For the encrypted image of Lena, the corresponding entropy is 7.9970bits. This means that the cipher-image is close to a random source and the proposed algorithm is secure against the entropy attack.

• C.    D fferent al attack

In general, attacker may make a slight change (e.g., modify only one pixel) of the plain-image to find out some meaningful relationships between the plain-image and the cipher-image. If one minor change in the plainimage will cause a significant change in the cipher-image, then the encryption scheme will resist the differential attack efficiently. To test the influence of only one-pixel change in the plain-image over the whole cipher-image, two common measures are used: number of pixels change rate (NPCR) and unified average changing intensity (UACI). They are defined as

У D ( I; j )

NPCR = =^-----x 100 % ,

W x H

UACI = —¹— [    | C^{1( 1} ’ j ) ^- C 2 ^{( i} ’ j )| ] x 100 %

W x H        255

, j where C1, C2 are the two cipher-images corresponding to two plain-images with only one pixel difference, W and H are the width and height of the processed image, D is a bipolar array with the same size as image C1 . D(i, j) is determined as: if C1(i, j) = C2(i, j), then D(i, j) = 0, otherwise D(i, j) = 1. NPCR measures the percentage of different pixels numbers between the two cipher-images whose plain-images only have one-pixel difference. UACI measures the average intensity of differences between the two cipher-images. To resist difference attacks, the values of NPCR and UACI should be large enough. The plain-image Lena is tested to show the two measures. Experimental results are depicted in Fig. 5. We can see from the figure that the NPCR is near 100% and the UACI is about 33% since the second round of encryption.

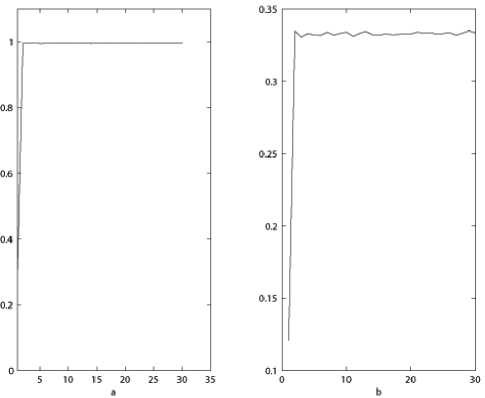
Figure 5. The NPCR and UACI tests. (a) NPCR test, (b) UACI test.

• D.    Resistance to cipher-image attacks

(a)

(b)

• IV. Conclusions

An efficient image encryption scheme based on 3D skew tent map and coupled map lattice is proposed in the paper. The proposed scheme utilizes the 3D skew tent map to shuffle the plain-image efficiently in the pixel positions permutation process, while employs the coupled map lattice system to change the gray values of the whole image pixels greatly. The performance analysis including key space analysis, statistical analysis, robustness against malicious attacks, such as cropping, nosing, JPEG compression, are carried out numerically and visually.

Acknowledgment

We thank anonymous referees for their constructive comments. This research was supported by National Natural Science Foundation of China (No. 11071152) and Natural Science Foundation of Guangdong Province (No. 10151503101000023).