A Chaos-based Pseudorandom Permutation and Bilateral Diffusion Scheme for Image Encryption

Published Online October 2014 in MECS

Thanks to the rapid growth of computer networks and the fast development in digital multimedia processing, more and more digital multimedia applications have covered most sectors of the society, such as education, communication, military, medical-care, etc. Especially, digital images are transmitted and shared in open networks due to their easy-understanding and attractive presentation natures. Digital information has become an indispensable resource and has changed people’s life totally. Some image information resources may contain valuable and highly sensitive message related to government public security or personal commercial interests. Therefore protection of digital image information against illegal copying and distribution has become extremely urgent. Encryption is a directly classical and efficient way to protect the digital information from unauthorized eavesdropping. In 1949, Shannon explained the encryption issue in his masterpiece [1], implying that the modern cryptology has been built. Since then, DES, IDEA, AES etc. were developed and became the typical data encryption standards [2]. However it has been shown that these ciphers are unfit for digital image information due to their special characteristics such as bulk data, high correlation among pixels, visual characteristics, etc [3].

Chaotic systems have many fantastic natures, such as ergodicity, good sensitivity to control parameters and initial values, pseudo-randomness, orbit inscrutability, which are in accordance with the fundamental requirements of cryptography. Therefore chaotic systems are suitable for constructing image encryption algorithms and chaos-based cryptosystems have attracted many researchers’ attention. As a matter of fact, chaotic maps can simulate random behavior in a quite impressive way. In particular, chaotic maps are easy to be implemented by microprocessors and personal computers. Therefore, chaotic cryptosystems generally have high speed with low cost, which makes them better candidates than many traditional ciphers for multimedia data encryption. In 1998, Fridrich firstly proposed one permutation-diffusion architecture based on different chaotic systems [3]. The proposed architecture is composed of two processes generally: chaotic confusion of pixel positions by permutation process and diffusion of pixel gray values by diffusion process, where the former permutes the plainimage pixel positions governed by a 2D chaotic map, while the latter changes the pixel gray values sequentially controlled by a 1D chaotic map, so that a tiny change for one pixel can spread out to almost all pixels in the whole image. The Fridrich architecture has become the most popular structure adopted in a great number of chaosbased image encryption algorithms subsequently proposed [4-8]. The existing chaos-based cryptosystems can be classified into two categories usually. The basic permutation units are pixel-level and bit-level for the first and second category respectively. So far, most of the cryptosystems fall into the first category. For example, Patidar et al. [7] proposed a secure and robust chaosbased pseudorandom permutation substitution scheme to encrypt color image. The proposed scheme contains three processes: preliminary permutation, substitution and main permutation. It demonstrates strong robustness and great security. All the three processes are done row-by-row and column-by-column instead of pixel-by-pixel to improve the speed of encryption. To yield excellent key sensitivity and plaintext sensitivity, both preliminary permutation and main permutation are designed to be dependent on the plain-image and controlled through the pseudo random number sequences (PRNS) generated from the chaotic standard map. The substitution process is initialized with the initial vectors generated via the cipher keys and chaotic standard map, and then the pixel gray values of row and column pixels of input 2D matrix are bitwise exclusive OR with the PRNS generated from the standard map. Ye and Guo [8] employed chaotic multimodal skew tent maps to design a chaos-based image encryption scheme with an efficient permutationdiffusion mechanism, in which permutation of the positions of image pixels incorporates with changing the gray values of image pixels by a two-way diffusion process to confuse the relationship between cipher-image and plain-image. All pixel-level ciphers suffer from a problem that the modifications to pixel gray values are all or almost dependent on the diffusion operations. However, diffusion operations usually consume more execution time than the confusion operations [9]. As for the second category, each pixel is divided into 8 bits for 256 gray-scale images. Since each bit of a pixel contains different percentage of the pixel information, the situation of performing confusion at bit-level is quite different from pixel-level case. The bit-level permutation not only relocates the pixel positions, but also alters the pixel gray values [10, 11]. Therefore certain diffusion effect has been introduced in the confusion stage with a bit-level permutation. Thanks to the superior characteristics of bitlevel operations and the intrinsic bit features of images, Zhang et al. proposed a novel image encryption scheme using lightweight bit-level confusion and cascade cross circular diffusion in [12]. They also applied an expand-and-shrink strategy at bit-level to shuffle the image with reconstructed permuting plane [13]. All the proposed image encryption schemes show good performances compared with the traditional permutation-diffusion structure operating at pixel-level. However, there exists one flaw in all bit-level based image encryption schemes. Although the bit-level confusion operations can change the pixel gray values, they consume much execution time to get the eight bit planes.

A good permutation process should show good shuffling effect and a good diffusion process should cause great modification over the cipher-image even if only a minor change for one pixel in the plain-image. However it has been pointed out that the proposed permutation-diffusion architecture with fixed parameters has one fatal flaw in [14], that is, the two processes will become independent if the plain-image is a homogeneous one with identical pixel gray value. Therefore, such a kind of encryption algorithms can be attacked by the following steps: (1) a homogeneous image is adopted to eliminate the confusion effect; (2) the keystream of the diffusion process is obtained via known-plaintext or chosen plaintext attacks; (3) the remaining cipher-image can be regarded as the output of a kind of permutation-only cipher, which has been shown insecure and can be cryptanalyzed by known-plaintext or chosen plaintext attacks [15, 16]. As a matter of fact, many existing chaosbased image encryption schemes with the permutationdiffusion architecture have been cryptanalyzed and have been found to be insecure due to the keystreams are nothing with the plain-images [17-21]. As a result, attackers can apply chosen/known plaintext attacks to break the ciphers easily. An ideal permutation-diffusion architecture should rely on the plain-images to be encrypted and thereby owns the one-time key effect.

In this paper, a robust and secure chaos-based image encryption scheme is proposed. The proposed image encryption scheme comprises of one permutation process and one diffusion process. To overcome the drawback of consuming much execution time to get the eight bit planes, we adopt a strategy to get the tradeoff between the workload and the security, that is, 4bits derived from the pixel gray value is regarded as one unit. In the permutation process, the image sized M x N is expanded to one of size M x 2 N by dividing the plain-image into two parts: one consisting of the higher 4bits and one consisting of the lower 4bits. To improve the speed of permutation process, another confusion operation is applied, that is, the permutation operations are done row-by-row and column-by-column instead of pixel-by-pixel or bit-by-bit. The chaotic cat map is utilized to generate chaotic sequences, which are quantized to shuffle the expanded image. The chaotic sequence for permutation process is designed to be not only dependent on cipher keys, but also dependent on plain-images, resulting in good key sensitivity and plain-image sensitivity. To achieve more avalanche effect and larger key space, a chaotic Bernoulli shift map based bilateral (i.e., horizontal and vertical) diffusion function is applied as well. The security and performance of the proposed image encryption scheme have been analyzed, including histograms, correlation coefficients, information entropy, key sensitivity analysis, key space analysis, differential analysis, encryption rate analysis etc. All the experimental results suggest that the proposed image encryption scheme is robust and secure and can be used for secure image and video communication applications.

The rest of the paper is organized as follows. In Section II, we first briefly introduce the 2D chaotic cat map and discuss its chaotic natures. Then we devote to designing the image encryption scheme. One permutation process and one bilateral diffusion process are presented to encrypt plain-images. In Section III, we present the results of security and performance analysis of the proposed image encryption scheme using histograms, correlation coefficients, information entropy, key sensitivity analysis, differential analysis, key space analysis, encryption rate analysis, etc. Section IV draws some conclusions for the paper.

II.  The Proposed Scheme

A. Chaotic cat map

Chaotic cat map is also called Arnold cat map. It is a two-dimensional invertible chaotic map introduced by Arnold and Avez [22]. The classical cat map is described by

0.9

0.8

0.7

0.6

0.5

Й^-Уу.^Д^^Й^^

,{•*•• •»’

i-

^xn +1

^yn +1

¹ if x n )

2 JI У п J

mod 1

0.4

0.3

0.2

0.1

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

where “ x mod 1 ” means the fractional part of a real number x by adding or subtracting an appropriate integer such that its result belongs to [0,1). Therefore ( x_n , y_n ) is confined in the unit square [0,1)² . The map is area preserving since the determinant of its linear transformation matrix is 1. As shown in Fig.1, the unit square is first stretched by the linear transform matrix and then folded back to the unit square by the modulo operation.

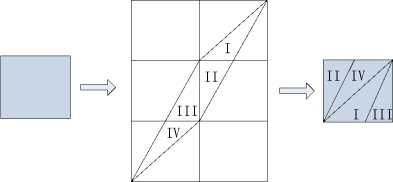
Fig.1 The chaotic cat map

(a) The orbit of (0.5231, 0.7412)

The above 2D cat map (1) can be generalized to the following form by introducing two real control parameters p >0 and p >0 [8]

x n + 1

. Уп + 1

q

P II x n I

I1 I mod 1.

¹+ pq Л У п J

The generalized cat map (2) has one Lyapunov characteristic exponent _{CT = t}, ^{1 + pq + pp 2 q 2 + 4 pq} larger 1₂

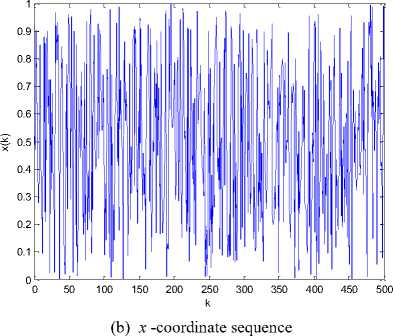
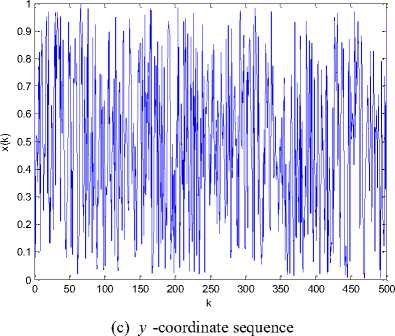
than one, so the map is always chaotic for p >0 , q >  0 [23]. The real control parameters in the generalized cat map results in enlarging the cipher key space for image encryption scheme significantly. It has good chaotic natures such as ergodicity, high sensitivity to control parameters and initial values, pseudo-randomness, orbit inscrutability, etc. Fig. 2 (a) shows an orbit of ( x ₀, y ₀) = ( 0.5231,0.7412 ) with length 1500 derived by the generalized Arnold map (2) with p = 5.324, q = 18.2, the x - coordinate sequence and the y - coordinate sequence of the orbit are plotted in Fig. 2 (b) and Fig. 2(c) respectively. Meanwhile, the sequences { x },{ y } have good randomness as well. Figs. 2(d)-(f) illustrate the pseudo-randomness of the yielded chaotic sequences.

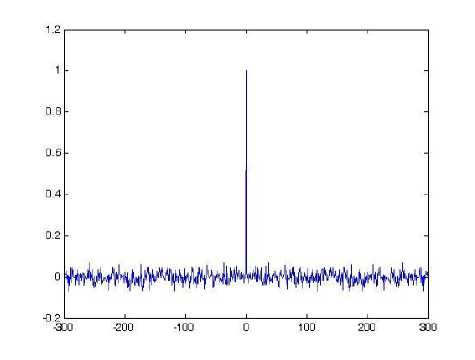
(d) The auto-correlation of x - coordinate sequence

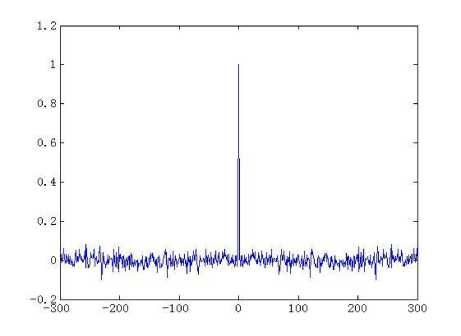
(e) The auto-correlation of y - coordinate sequence

higher four bits are extracted to form part I of size M x N as well.

• (2)    The lower 4 bits are extracted to form another new pixel set shown as part П in Fig. 3. We note that the lower 4 bits of each pixel contains only 5.875% of the total information of the considered pixel.

The two subsets then form a new plain-image NP with size M x 2 N and gray-scale level 16.

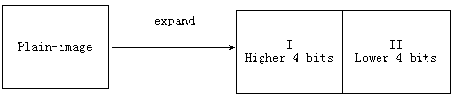
Fig.3. The expansion of plain-image

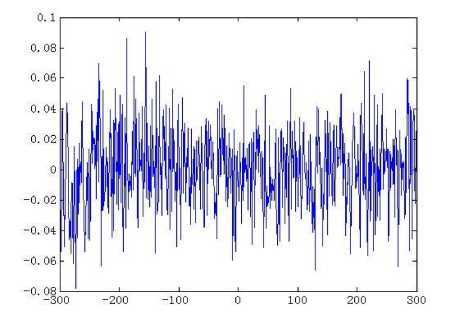
(f) The cross-correlation of between x - coordinate sequence and y - coordinate sequence

Fig.2. Chaotic natures of the generalized Arnold map with p=5.324, q=18.2.

• B.    Permutation process

In this stage, 2D generalized chaotic cat map (2) is employed to generate pseudorandom sequences, which are quantized and then utilized to shuffle the plain-image. We discuss the detailed permutation process step-by-step. Through the paper, we assume the plain-image to be encrypted is of size M x N = 512 x 512.

Step 1. Read a 256 gray-scale level plain-image with size M x N , then expand this plain-image to a new image with size M x 2 N and 16 gray-scale level. The expansion strategy is as follow. The plain-image is divided into 2 parts, the higher 4 bits are treated as one part and the lower 4 bits are integrated into the second part. Therefore 8bits of each pixel can be divided into 2 groups as shown in Fig. 3.

• (1)    The higher 4 bits are extracted to form a new pixel set; each pixel gray value contains 4 bits, which are originally the 8th, 7th, 6th, and 5th bit in the plain-image

with corresponding weights 128 , respectively. The higher 4 bits of each 128 + -64 + — + — = 94.125% of the pixel 256  256  256256

32      16

256 ,   256

pixel carry information.

Regarding one plain-image with size M x N , all the

Step 2. We shuffle the expanded plain-image using a strategy via row-by-row, column-by-column instead of pixel-by-pixel, resulting in the improvement of execution efficiency. In traditional chaos-based image encryption schemes, the keystreams generated by the cipher keys are nothing with the plain-images, and therefore they fail to provide sufficient security and can be cryptanalyzed by known/chosen plaintext attacks. To enhance such a kind of security, we adopt an improved strategy. The chaotic sequences for permutation process are made to be dependent on both plain-image and cipher keys, and thereby get excellent key sensitivity and plaintext sensitivity. First, we calculate the number N of iterations for generalized cat map by Eq. (3). Then we iterate the generalized cat map N times starting with the initial conditions ( x ₀, y₀ ) and get ( x_{N t}, y_{N t} ) .

N = { NP (1,1) + NP (1,2) +L + NP (1,2 N ) +

NP (2,1) +L + NP ( M ,2 N )}mod256.      (3)

For simplicity, we still denote ( x_Np y_{N t}) as ( x , y ) . The generalized cat map is then applied to generate four chaotic sequences. The pseudo code is outlined as follows.

for i= 1 to max (M,2N) step 1

x ' = ( x + p x y )mod1

y ' = ( q x x + (1 + p x q ) x y ) mod 1

PR1( i ) = 1 + floor( x ’x M )

PC1( i ) = 1 + floor( y x 2 N )

x = ( x ' + p x y ’)mod1

y = ( q x x ' + (1 + p x q ) x y ')mod1

PR 2( i ) = 1 + floor( x x M )

PC 2( i ) = 1 + floor( y x 2 N )

end for i=1 to M step 1

interchange NP(PR1(i),:) and NP(PR2(i),:) end for i=1 to 2N step 1

interchange NP(:,PC1(i)) and NP(:,PC2(i)) end where NP(i,:) and NP(:,j) represent all the elements of ith row and jth column of NP respectively; function floor(x) rounds x to the nearest integers towards minus infinity. interchange NP(PR1(i),:) and NP(PR2(i),:) stands for exchanging the PR1(i)th row and PR2(i)th row. In this process, the generalized cat map is iterated with randomly selected control parameters and initial conditions

(p , q ) = (102.456789321, 92.234569217),

( x_Q , y_Q ) = (0.123456 789, 0.234567891).

• C.    Diffusion process

In the diffusion stage, in order to enhance the resistance to statistical attacks and differential attacks efficiently, we design a bilateral diffusion with horizontal and vertical direction as shown in Fig. 4. After this process, the histogram of the cipher-image is extremely uniform and completely different from that of plainimage. The diffusion process is outlined as follows.

Step 3. After the permutation process, we get a shuffled image B with size M x 2 N . In this step, we shrink image B into image C with size M x N , which is actually the reverse procedure of the expansion procedure. The pixel values locating in part I will become the 8th, 7th, 6th, 5th bit of the corresponding pixel of the shrunk image C . The pixel values locating in part П will become the 4th, 3rd, 2nd, 1st bit of the corresponding pixel of image C . We depict the procedure in Fig. 5.

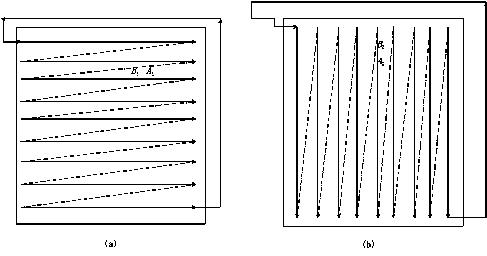
Fig.4. The bilateral diffusion diagram.

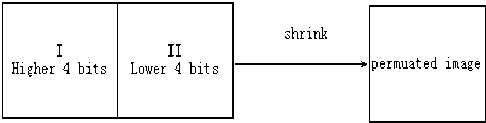
Fig.5. The shrinkage process.

Step 4. Generate two random positions A = (px^ px) , A = (p2„, p2) as the start pixels of the diffusion operation in two different directions by the chaotic cat map. The motive is to enhance the security and randomness. They are calculated by p1 x = (floor (65^1(100) x109))mod M, pXy = (floor (bsm2 (100) x 109)) mod N, Pix = (floor (bsmx (101) x109))mod M, Piy = (floor (bsm^ (101) x 109)) mod N,

where bsm ( s ) , bsm ( s ) are respectively the s th pseudorandom number of the chaotic sequences generated by Bernoulli shift map [24]

bsm_k ( i + 1) = ( bsm_k ( i ) / c ) mod 1, k = 1,2    (5)

with two initial values and one same control parameter bsm (0) =0.12345432167893, bsm (0) =0.887 65432123456, c =0.56789.

Step 5. The 2D gray value matrix C is first transformed to one vector V . Starting from the initial position A to the end position BY = (pY„, px -1) , the first diffusion round is performed orderly according to the horizontal direction shown as Fig. 4(a). The diffusion is governed by tx (i) = [ c (i )/(1000 x c )]mod1, lj (i +1) = (floor (tj (i) x1000) + R (i +1)) mod 256,   (6)

c (i +1) = V (i +1) ® l (i +1), where c (i) and c (i +1) are the previous and current gray value of the ith pixel and i+1th pixel of the output encrypted image, V(i) is the value of the ith element of vector V . t(i) and l(i) are temporary variables. The initial condition c (0) should be set one value to make the diffusion function definite, which can be regarded as part of cipher keys and defined here by c (0) = floor ([(Key1/c )mod1]x109)mod256.

With Key 1=0.5678912342321 and the same control parameter c =0.56789. Chaotic sequence { R ( i )} is generated by

R ( i ) = floor ( l ( i ) x 10 9 ) mod 256 ,         (7)

where l(i) is the output sequence of the Bernoulli shift map l (i + 1) = (l (i)/ c )mod1              (8)

with initial value l (0) =0.25673548982132 and control parameter c , respectively.

Step 6. In the second diffusion round, the diffusion direction is illustrated in Fig. 4(b) where we start from the pixel A to the end pixel B2 = (p2x -1, p2). The second diffusion round is performed as follows.

Ц (i) = [ c2 (i)/ (1000 x c )]mod1, l2 (i +1) = (floor (t2 (i) x 1000) + R'(i +1)) mod 256,  (9)

c2 (i +1) = c (i +1) Ф l2 (i +1), where c(i) is one-dimensional vector obtained by the first diffusion round in Step 5, c2 (i)and c2 (i + 1)are the previous and current gray value of the ith pixel and i+1th pixel of the output cipher-image at the second diffusion round, t(i) and l(i) are temporary variables and the initial condition c (0) is set to be c (0) = {[(Key 2 / c) mod1] x 109} mod 256

where Key 2=0.33792252345612. The sequence { R '( i )} is generated by

R '( i ) = floor ( l '( i ) x 10⁹) mod256         (10)

where l '( i ) is the output sequence of Bernoulli shift map

(d) Histogram of cipher-image

Fig. 6. The encrypted results.

l '( i + 1) = ( l '( i )/ c )mod1               (11)

with initial value l '(0) =0.48982132256735 and control parameter c , respectively.

The complete image encryption scheme is composed of the permutation process and the bilateral diffusion process. The plain-image Lena with size 512X512 and its cipher-image are shown in Fig. 5(a), (b) respectively.

(a) Plain-image of Lena

(b) Cipher-image of Lena

• III.    Security And Performance Analysis

In this section, security and performance analysis for the proposed image encryption scheme have been carried out, including histograms, correlation coefficients, information entropy, key sensitivity analysis, key space analysis, differential analysis, encryption rate analysis. Some comparisons with two other existing algorithms are done as well. Two comparable schemes proposed in [2] are Traditional Chaos-based Image Encryption Architecture (TCIEA) and Lightweight Bit-level Confusion and Cascade Cross Circular Diffusion Encryption Scheme (LBCCC).

• A.    Histogram analysis

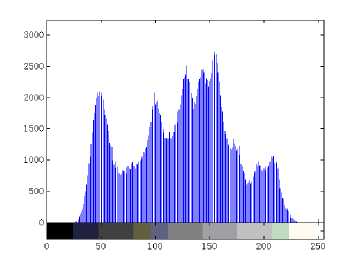
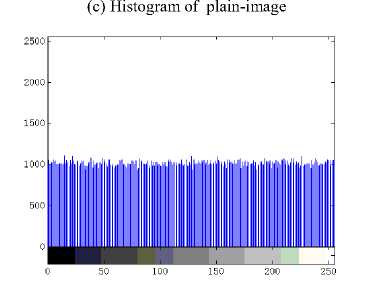
Histogram analysis is a visual test which reveals the distribution information of pixel gray values. A good encrypted image should have a uniform and completely different histogram in comparison with that of the plainimage. As shown in Figs. 6(c)-(d), the histogram of the cipher-image obtained by the proposed image encryption scheme is fairly uniform and is significantly different from that of the plain-image. Therefore, the proposed image encryption scheme does not provide any useful information for the opponents to perform any effective statistical analysis attack on the cipher-image.

• B.    Correlation analysis

It is common sense that for an ordinary nature image having definite visual content, each pixel is highly correlated with its adjacent pixels either in horizontal, vertical or diagonal direction. An ideal encryption technique should produce cipher-images with less correlation in the adjacent pixels. To quantify and compare the horizontal, vertical and diagonal correlations of adjacent pixels in the plain and cipher images, we calculate the correlation coefficients for all the pairs of horizontally, vertically and diagonally adjacent pixels respectively. First, we select 6000 pairs of two adjacent pixels randomly from an image, and then calculate the correlation coefficient by the following formulae

E {[ X - E ( X )][ Y - E ( Y )]}

X,Y          D(X) D(Y)

1T

E(X) =  £x, D(X) = -£[x-E(X)]2,(12)

T i=1

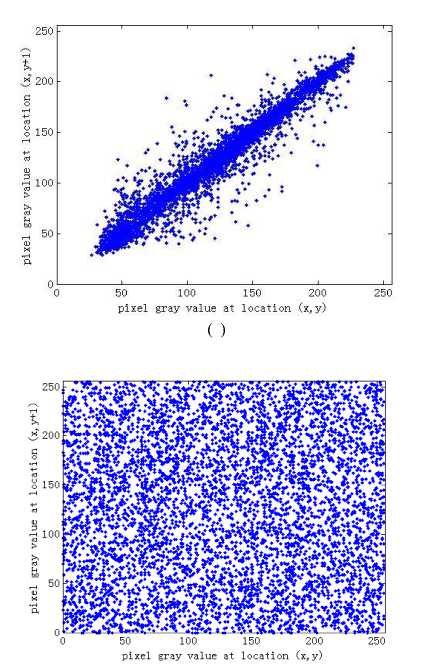
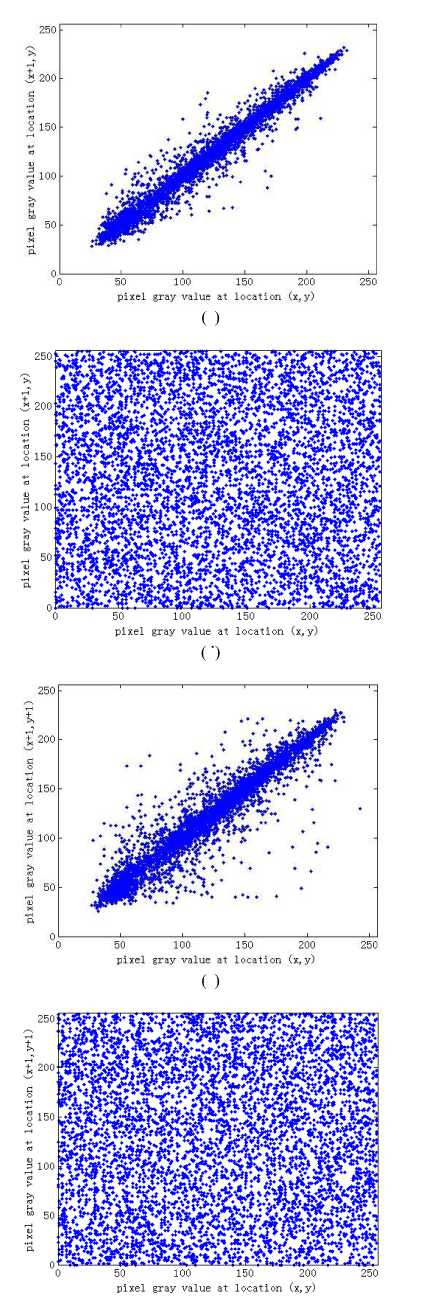
where X = ( x ,L , x_T ), Y = ( y_x ,L , y_T ) are the gray values of two adjacent pixel pairs. T is the total pair number, E ( X ), D ( X ) are the expectation and variance of X , respectively. In the simulations, two test images Lena and couple are used. The correlation coefficients for two test images derived from the proposed scheme and two comparable schemes are listed in Table 1. The correlation distributions of two adjacent pixels in the plain-image Lena and that in its corresponding cipher-image are show in Fig. 7. We can conclude that the correlation between adjacent pixels is greatly reduced in the cipher-image.

(a)

(b)

(c)

(d)

(e)

(f)

Fig.7. Correlations of two adjacent pixels in the plain-image and in the cipher-image: (a),(c),(e) are for the plain-image; (b),(d),(f) are for the cipher-image.

• C.    Differential attack analysis

The differential cryptanalysis of a block cipher is the study of how differences in a plaintext can affect the resultant differences in the ciphertext with the same cipher key. It is usually done by implementing the chosen plaintext attack but now there are extensions which use known plaintext as well as ciphertext attacks as well. As for image cryptosystems, attackers may generally make a minor change (e.g., modify only one pixel) of the plainimage and encrypt the original plain-image and the modified plain-image using the same cipher keys, then compare the two cipher-images to find out some meaningful relationships between the plain-image and the cipher-image. If a meaningful relationship between plainimage and cipher-image can be found in such analysis, which may further facilitate the attackers to determine the cipher key. If one minor change in the plain-image will cause significant, random and unpredictable changes in the cipher-image, then the encryption scheme will resist differential attack efficiently. To test the robustness of image cryptosystems against the differential cryptanalysis, two most common measures NPCR (number of pixel change rate) and UACI (unified average changing intensity) are used. NPCR is used to measure the percentage number of pixels in difference in two cipherimages obtained by applying the same cipher key on two plain-images having one pixel difference only.

NPCR for a cryptosystem is defined by

D ( i , j ) =

S D ( i , j )

NPCR = -j -----x 100% ,

M x N

• 1,    C 1 (i , j ) * C 2 ( i , j ),

0,       otherwise ,

where M , N are the height and width of the considered image; C and C are the two cipher-images corresponding two plain-images with only one pixel difference.

The NPCR for two random images, which is an expected estimate for an ideal image cryptosystem, is given by

NPCR Expected = (1 - 2 - ' ) X 100%,         (14)

where L is the number of bits used to represent all the intensity levels. For a 8-bit gray-scale image, L = 8 , hence NPCR Expected = 99.6094%.

UACI, the average intensity difference between two cipher-images C and C , is calculated by

1          C ( i , j ) - C ( i , j )|

UACI =------[У      --- 212ZZ1 ] x 100%.  (15)

M X N tj*     255

The UACI for two random images, which is an expected estimate for an ideal image cryptosystem, is given by

1   У² L ^-1 i ( i + 1)

UACI Expected =     .^ - = 1 L_₁    X 100%.      (16)

For a 8-bit gray-scale image, UACI^_cted = 33.4635% .

We randomly choose 10 pixels and calculate the corresponding NPCR and UACI values using the proposed image encryption scheme and two comparable schemes TCIEA and LBCCC. The experimental results are listed in Tables 2-3.

Table 1. Correlation coefficients of the proposed and comparable schemes.

Test image	Direction	Plain-image	TCIEA	LBCCC	Proposed scheme
Lena	Horizontal	0.9725	-0.0096	0.00032795	0.0079
	Vertical	0.9857	-0.0015	0.0085	-0.0063
	Diagonal	0.9571	0.0099	-0.0145	0.0114
Couple	Horizontal	0.9509	-0.0011	-0.0256	0.0036
	Vertical	0.9595	-0.0100	-0.0136	-0.0167
	Diagonal	0.9144	0.0035	0.0066	-0.0093

Table 2. NPCR and UACI performance with one round encryption.

(a) Proposed Scheme

position	(27,461)	(340,158)	(72,504)	(69,380)	(450,246)	(307,303)	(57,468)	(152,288)	(62,295)	(325,19)
NPCR(%)	75.4379	76.1227	75.0801	75.7126	27.8019	74.6811	74.4827	39.0640	3.7609	28.7197
UACI(%)	25.1066	25.3403	25.0485	25.1682	9.3086	24.8565	24.7459	12.9700	1.2586	9.5515

(b) TCIEA

position	(27,461)	(340,158)	(72,504)	(69,380)	(450,246)	(307,303)	(57,468)	(152,288)	(62,295)	(325,19)
NPCR(%)	0.1171	0.3582	0.0488	0.0095	0.3418	0.0290	0.0366	0.4185	0.0214	0.1217
UACI(%)	0.0386	0.1222	0.0168	0.0033	0.1162	0.0099	0.0128	0.1426	0.0073	0.0404

(c) LBCCC

position	(27,461)	(340,158)	(72,504)	(69,380)	(450,246)	(307,303)	(57,468)	(152,288)	(62,295)	(325,19)
NPCR(%)	57.8312	10.3382	54.4086	37.4802	57.7965	53.2101	54.3964	23.5035	2.1427	35.9169
UACI(%)	19.4888	3.4672	18.2960	12.6269	19.4928	17.9483	18.3201	7.9558	0.7384	12.1110

Table 3. NPCR and UACI performance with two rounds encryption. (a) Proposed Scheme

position	(27,461)	(340,158)	(72,504)	(69,380)	(450,246)	(307,303)	(57,468)	(152,288)	(62,295)	(325,19)
NPCR(%)	99.5922	99.6113	99.6231	99.5888	99.6078	99.6078	99.5876	99.6201	99.5991	99.6101
UACI(%)	33.4768	33.4530	33.5106	33.4430	33.5070	33.4600	33.4473	33.4362	33.4421	33.4023

(b) TCIEA

position	(27,461)	(340,158)	(72,504)	(69,380)	(450,246)	(307,303)	(57,468)	(152,288)	(62,295)	(325,19)
NPCR(%)	34.7233	67.2276	17.3740	2.5234	65.9348	10.4897	12.0281	68.7874	8.9283	37.0251
UACI(%)	11.7293	22.6670	5.8478	0.8333	22.1911	3.5486	4.1126	23.2377	3.0118	12.4871

(c) LBCCC

position	(27,461)	(340,158)	(72,504)	(69,380)	(450,246)	(307,303)	(57,468)	(152,288)	(62,295)	(325,19)
NPCR(%)	99.6078	99.5956	99.5979	99.5926	99.6090	99.6178	99.6304	99.6124	99.5934	99.5937
UACI(%)	33.4520	33.3745	33.4841	33.5222	33.4765	33.4651	33.4371	33.5834	33.3996	33.4644

• D.    Information entropy analysis

Information entropy is a measure of the uncertainty associated with a random variable and can also be a measure of disorder and randomness. It quantifies the amount of information contained in data, usually in bits/symbol. Two extremely cases are: a long sequence of repeating characters and a truly random sequence. The former has entropy of 0 since every character is predictable, and the latter has maximum entropy since there is no way to predict the next character in the sequence. Regarding image, it can be used to measure the uniformity of image histograms and the randomness of image information. The entropy of a message source m can be measured by

2 L - 1                      1

H ⁽ m ) = 2 p ( m Dlog——7,         ⁽¹⁷⁾

i = 0              p ⁽ mi )

where L is the number of bits required to represent a symbol in the message m , p(m) represents the probability of occurrence of symbol m and log denotes the base 2 logarithm so that the entropy is expressed in bits. For a random source emitting 256 symbols, its entropy is H(m) = 8 bits. The best expected value of information entropy for an 8-bit cipher-image is 8, indicating the cipher-image can be considered as random one. We have calculated the information entropy for plain-images Lena, couple and their corresponding cipher-images. The results are shown in Table 4. The information entropy data produced using two comparable cryptosystems are listed as well.

• E.    Key space analysis

A good image encryption scheme should be extremely sensitive to cipher keys, which is an essential feature for any good cryptosystem in the sense that it can effectively make brute-force attacks infeasible. The key sensitivity of a cryptosystem can be observed in two ways: (i) the cipher-image derived from the cryptosystem should be extraordinarily sensitive to cipher keys, i.e., if we use two slightly different cipher keys to encrypt the same plainimage, then two produced cipher-images should be almost different and possess negligible correlation; (ii) the cipher-image cannot be decrypted correctly although there is a slight difference between the encryption and decryption keys. In the proposed scheme, the key space is composed    of    all    possible    choices    of p, q, x , y , bsm (0)  , bsm (0) , c, l(0), l'(0) , Key1

and Key 2 .

To test the sensitivity of cipher key parameter k , the original plain-image Lena is encrypted with k , k - A S , k + AS respectively while keeping the other cipher key parameters unchanged. The key sensitivity coefficient is calculated by

P ' , ( k ) = £ [ N s ( 1 1 ( i , j ), 1 2 ( i , j )) + N s ( 1 1 ( i , j ), 1 3 ( i , j ))]

p' tk)                           Г 1, x ^ y ,

P s (k) = Л '   ^x 100%, N s ( x , У ) = L, y ,      (18)

• 2 x M x N                  [ 0, x = y ,

  where I , I , I are the encrypted images respectively, and AS is the perturbing value. The test results are shown in Table 5. We have also test the sensitivity of Key 1 and Key 2. As AS = 10 ^{- 7}, the corresponding p_s ( k ) are only 0.6681  and 0.6680 respectively. The

  experimental results show that these two keys are of low sensitivity and therefore cannot be considered to be cipher keys. The other parameters are all strongly sensitive and can be regarded as cipher keys. The key space is therefore larger than (10¹⁴)⁷ x (10¹³)² = 10¹²⁴ . Such a key space is large enough to stand brute-force attacks. The sensitivity test can also be demonstrated visually, for example, see Fig. 8.

Table 4. Information entropy of the proposed and two comparable schemes.

Test image	Proposed scheme	TCIEA	LBCCC
Lena	7.99930930933	7.9992544486	7.9992049214
Couple	7.99701882136	7.9972668082	7.9974865480

Table 5. Result of the sensitivity test ( ^{A S} = ¹⁰ for ^P , q and ^{A S  10} for the other cipher keys).

k	bsm (0)	bsm (0)	x 0	y 0	c	l (0)	l '(0)	p	q
ps ( k )	0.9962	0.9961	0.9960	0.9962	0.9962	0.9960	0.9961	0.9963	0.9960

(a) Original image

(c) Encrypted image with x _o =0.123456789+ 10 ¹

(b) Encrypted image with x =0.123456789

(d) Original image

(e) Encrypted image with c =0.56789

(f) Decrypted image with c =0.56789

(g) d ecrypted image with c =0.56789+ 10 ^{- 14}

Fig. 8. Key sensitive test.

• F.    Resistance to known-plaintext and chosen plaintext attacks.

In the permutation process, we calculate the number N and then iterate the chaotic cat map N times to get (x, y)to generate chaotic sequences for permuting the plain-image. Since N depends on all the values of NP(i, j),1 ≤ i ≤ M,1 ≤ j ≤ 2N , (x, y) are then related to the plain-image and consequently the yielded chaotic pseudorandom sequences for permutation rely on the plain-image as well. When different plain-images are encrypted, the corresponding chaotic sequences applied to permute the plain-images will be different, resulting in different cipher-images. The attackers cannot find useful information by encrypting some special images. The proposed image scheme can resist the known/chosen plaintext attacks efficiently.

• G.    Speed performance analysis

We have also estimated the encryption rate of the proposed image encryption scheme. An encryption round of the proposed image encryption scheme is composed of one confusion process and one bilateral diffusion process. Two comparable image encryption schemes are performed as well on a computer with Intel Core 2GHZ CPU and 1 GB RAM. The operating system is windows XP and the simulation software is MATLAB 7.2 programming. In Table 6, all the execution time for three image encryption schemes is listed.

Table 6. Execution time comparison.

Scheme	Time (s)
Proposed	0.957
TCIEA	0.656
LBCCC	1.041

From Table 6, we can know that the execution time of proposed scheme is shorter than the LBCCC’s. Although the TCIEA scheme execution time is shortest, its NPCR and UACI values cannot achieved the ideal values even at the second encryption round. Therefore, we can be concluded that the proposed scheme have higher efficiency.

• IV.   Conlusions

A novel chaos-based pseudorandom permutation and bilateral diffusion scheme for image encryption has been proposed. The pseudorandom number sequences produced via 2D chaotic cat map and generalized Bernoulli shift map have been used in an effective way to achieve the desired level of confusion and diffusion in the encryption process. The permutation process has been made to be dependent on the plain-images as well as cipher keys, which produce an excellent combination of plain-image sensitivity and key sensitivity in the encryption technique. The performance and security of the proposed image encryption technique, including histograms, correlation coefficients, information entropy, key sensitivity analysis, key space analysis, differential analysis, encryption rate analysis. etc. have been tested thoroughly using rigorous security analysis tools commonly used in the image processing as well as chaosbased cryptosystems. The results are perfect as required for any secure image and video communication application.

Acknowledgment