A chaotic cryptosystem using conjugate transcendental fractal function

Now days, multimedia transmission became common in every aspect of communication like military, picture messaging application for cell phones, biological data, medical imaging, scientific observation, etc. With the advancement in the internet and computer technologies, a rapid transmission occurs over various transfer networks. A secure communication system is essential to achieve a reliable multimedia circulation.

A cryptographic system is a key component to realize the requirement of a secure system and achieved by transferring the encrypted data over the unsecure network. The received data can only be readable by decrypting it with the help of a security key at the other end. Image encryption is a part of a cryptographic system in which a scrambled form of an input image is created, which is unidentifiable by an unauthorized user [1].

Developing an image encryption algorithm, is inevitably a challenging job as compared to encrypting a textual data. An image size is a critical challenge in terms of an acceptable time frame while executing an algorithm. The image also has a high correlation value between its adjacent pixels which can be used in cryptanalysis. A competent image encryption algorithm must be able to distribute image pixels uniformly in the cipher image to increase the randomness. Various parameters are used to prove the effectiveness of the cryptographic method, which in turn, achieve the required level of accuracy and security.

Considering the notable characteristics of a chaotic system, like non-periodicity, butterfly effect (sensitive to the initial condition), ergodicity and pseudo-randomness attract the researchers to utilize the feature in the design of a cryptosystem. The chaotic map plays a crucial role to introduce confusion and diffusion between the image pixels. Sometimes, 1D-chaotic maps like Tent, Logistic, and Sine map are good enough to produce the required confusion and diffusion impact during the process execution [2–3]. But the chaotic orbits and initial values of the said maps (i.e. 1D chaotic maps) may be analyzed by the unauthorized person to eavesdropping the system [4–6]. Later, multidimensional chaotic maps such as Arnold, henon, 2D Logistic etc. with enhanced chaotic performance were introduced by the researchers. However, a combined form of 1D chaotic maps has also been successful to obtained a secure and reliable cryptosystem [7–9]. Rhouma et al. analyzed the weaknesses and possible security attacks on the cryptosystem designed using the high-dimensional chaotic map [10–11].

A fractal image is the graphical presentation of a complex structure at local and global irregularity level [12]. It is generated by iterating a mathematical function for pre-determined number of times. A fractal image possesses high variation in detail at discrete scales, also determines a wide choice in terms of key space. Few real-life examples are cauliflower, coastlines, clouds, tree, etc.

A well-known fractal introduced by Benoit Mandelbrot, in 1979, is a set of complex points in which the boundary exhibits a different structure at each scale, known as Mandelbrot set [13]. The Mandelbrot set (MS) fractal can be defined as “The MS fractal is designed by iterating a simple mathematical function z² + c for which the value c remains within the boundary and does not escapes to infinity.” Similarly, a Julia set fractal is formed by using the same mathematical function i.e. z² + c . But, the Mandelbrot set draws a fractal image by assigning z = 0 and varying c for each pixel, whereas, for each c value of MS fractal, a Julia set fractal will be formed using a non-zero z value [14]. At each pixel in Mandelbrot set, a distinct Julia set image is obtained. One pixel shifting in Mandelbrot function will generate a totally different Julia image, consequently, a unique key sequence will be generated. Many researchers considered the fractal structure and applied in various applications such as graphic design, medical, antenna design, image encryption, etc. Unlimited resources are available to design the fractal images including parametric program.

The paper aims to provide a secure cryptosystem by utilizing a chaotic map recently suggested in an image encryption method. The author [15] proposed a 2D Sine Tent composite map (2D-STCM) to create a chaotic key sequence which considers better trajectory than the other maps. Here, the method used the same chaotic map, but the initial condition used by 2D-STCM are generated by iterating the CTFF using Picard, Mann and Ishikawa iteration method separately. As a result, three distinct chaotic key sequences have generated after executing 2D-STCM. Further, the key stream is scanned using zigzag scanning method separately. Conclusively, a security key is obtained by XORing the three-scanned chaotic key sequences. In the next phase, a diffusion process is implemented to modify the image pixel values and thus break the correlation between the adjacent image pixels. The encrypted images are analyzed using various parameters such as histogram distribution, entropy, correlation coefficient, NPCR, UACI, MSE, and PSNR.

The rest paper is discussed as follows. In section 2, previous work on image encryption is discussed. The design of the newly suggested cryptosystem is illustrated in section 3. Section 4 presents the performance analysis of the proposed method to prove its efficacies towards the real-life applications. The last section concludes the paper by summarizing the finding of the given scheme.

• II.    Related Work

  Since 1990s, researchers have employed a chaotic system in the design of a cryptosystem after observing its characteristics. In 2000, Fidritch has patented a chaotic cryptosystem to encrypt the data such as image using two and three-dimensional chaotic Baker map [16]. To encrypt the data/image, single dimensional as well as multidimensional chaotic map has been extensively used

in various research. An image encryption method was proposed by the author by combining two 1D chaotic map to have better chaotic behavior [17].

To encrypt an image, Benyamin used a hyper-chaotic system to generate a key sequence. The algorithm comparatively faster due to the single round of diffusion [18]. Whereas, in [19], hyper-chaos shuffled the plain image and then compress and diffuse the shuffled image by applying Chinese remainder theorem. In [20], a color image encryption algorithm proposed by using coupled-map lattices (CML) and a fractional-order chaotic system to increase the robustness and security of the system. A combination of two or more chaotic maps were also analyzed to enhance the complexity of the cryptosystem [21]. The two Logistic sequences were used to label the row coordinates and column coordinates of scrambled image and then MOD and XOR operations were applied to diffuse the plain image [22]. A noisy Logistic map provides the set of initial values to the Clifford strange attractor function to shuffle the pixel position and pixel values of a plain image in Navy [23]. The researchers always explore the new possibilities to provide better system in each domain. In [24], the author introduced a new Beta chaotic map based on Beta function to generate a key sequence. A parametric switching chaotic system is responsible for image pixel substitution and permutation and encode the given image to encrypted image [25]. It is suggested that the image encryption method should consider a set of complex operations to design a secure cipher [26]. However, permutation only image cipher is fragile to known-plaintext attack [27].

Since researchers are known to innovate new ideas by experimenting in a different way. The authors combined a chaotic system with DNA sequence and then applied confusion and diffusion process [28–30]. In ref. [28], the plain image pixels are bit XORed using the pseudorandom sequence formed by the spatiotemporal chaotic system CML (coupled map lattice). Then a DNA permutation and DNA confusion process have been executed to completely reshuffled the original image. Recently, author [29] utilized the concept of ACP (Artificial societies, Computational experiments, Parallel execution) given by Fei-Yue Wang and performed the encryption process in two steps. The chaotic data in reality and chaotic data in simulation were used to convert artificial random image and original image respectively. To obtain a cipher image, performed DNA-XOR operation on the combined impact of the applied chaotic data of two groups. A DNA arrangement is used as a key sequence to permute and diffuse the plain image matrix [30]. To encrypt an image, the author utilized chaotic random phase masks, Gyrator transform and Jigsaw transform along with the random permutation of resulting image [31]. A new phenomenon, i.e. particle swarm optimization is introduced with the logistic map to optimize the encrypted image to get improved performance results. The approach helps to minimize the correlation coefficient value between image pixels, hence exhibits the optimum efficacy as compared to other image encryption method [32]. Also the chaotic map helps to encrypt medical images as well [33].

Fractal geometry helps to enhance the complexity of the cryptosystem design due to its complex mathematical structure. Initially, in 2003, a team designed a cryptosystem to encrypt a message using random numbers and Mandelbrot set fractal. At that time fractal was not so much popular in the cryptography system. Author succeeds to encrypt the data, but unable to decode the same. A perfect decoder required a mapper so that no number came out twice [34]. Later, in 2004, an approach was suggested to use fractal based encryption/decryption key and USA navy published the patent for the same [35]. There are numerous fractal functions, that can be employed in many applications such as Mandelbrot set, Julia set and more [36]. In this paper a conjugate transcendental fractal function is used to create a set of initial values. A detailed analysis of Mann iterated CTFF with respect to cosine function has been carried out by the author in [37]. The finding of the paper includes beautiful fractal images and the presence of tricorn and Mandelbrot set images on the external rays. The author analyzed the fractal structure and then utilized the fractal geometry to encrypt the predetermined length of the message [38]. Although, Suthikshn [39] applied RSA to encrypt the message using a secret key generated from the Mandelbrot set fractal.

A compression-encryption scheme was proposed by the author in which a fractal dictionary encoding pattern is applied to compress an image followed by XOR operation using JuliaStreamCipher and a diffusion step [40]. A finite field cosine transformation (FFCT) and multi-fractal images based private key encryption algorithm was suggested by the researcher in [41]. In FFCT phase, a plain image is transformed into a temporary cipher image, which is further encrypted using a secret key obtained through multi-fractal images. Similarly, in [42], a system key was generated by using multiple fractal images by adding feedback delay, multiplexing and independent horizontal and vertical shifts in the process. However, a cryptosystem was designed by using different keys at each iteration to encrypt the image [43]. A fractal function can be used in conjunction with the chaotic map to introduce more randomness and butterfly effect. An idea has been suggested by the author in which the initial values provided to the 2D composite chaotic map by iterating a fractal function [15]. The paper presents an image encryption method which combines the features of fractal function, chaotic map and the zigzag scanning method to create a key sequence. Further, image cipher obtained after performing algebraic transformation on plain image using the secret key sequence.

• III.   The Proposed Cryptosystem

The proposed cryptosystem consists of two major steps:

• 1.    Generation of a security key

• 2.    Convert plain image into cipher image

• A.    Key Stream Generation

The secret key used in the proposed cryptosystem is obtained in three steps: 1) a set of initial values using CTFF, 2) key sequence using 2D-STCM, 3) zigzag scanning of chaotic key sequences.

The fractal images are designed by using the feedback system in which at each iteration, outcome of each operation becomes the input to the same system [12]. It can be characterized as:

One-step feedback machine is considered by Peano– Picard iteration method. Let Z be a nonempty set of complex variable and f : Z → Z . For any point x0 ϵ Z , the equation can be represented as:

Zn+1 = f(Zn),n > 0 (1)

In two-step feedback machine, The function z_n+1 = f(z_n, z_n-1), requires two numbers as input and returns an output [44]. For the same point x0 ϵ Z , the Mann iterated sequence {z_n} is defined by [45]:

Zn+1 = S * f^Zn) + (1 - s) * Zn,n > 0 (2)

Also, the Ishikawa iterated set of sequence {yn} and {xn} is defined by [46]:

Уп = s' *f(Xn) + (1 — s') *Xn,n > 0 (3)

Xn+i = s * f (yJ + (1 — s) * Xn, n > 0 (4)

Where 0< s ≤1 and 0< s’ ≤1, and s and s’ both must be non-zero numbers. In fact, for s = 1, Mann iteration reduces to Picard’s iteration, and for s’ = 1, the Ishikawa iteration reduces to Mann’s iteration and for s = s’ =1, the Ishikawa iteration reduces to Picard’s iteration.

The function f( z) can be a quadratic, cubic, or biquadratic polynomial. Here the function f(z) is:

zn+1 = con;(sin(zn)) + c (5)

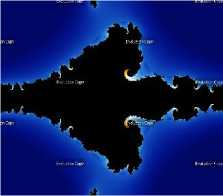
Where c is a complex variable. The fractal image will be obtained by repetitive iteration of the transcendental conjugate function for n times. The paper generates three sets of preliminary values by iterating the above given function using Picard, Mann, and Ishikawa iteration method respectively. Fig. 1 shows the images of executing the fractal function with reference to the above said iteration methods using Ultrafractal^TM software (Please ignore evaluation word in the images).

The paper used the Picard iterated, Mann iterated, and Ishikawa iterated transcendental fractal function to get three different sets of preliminary values so that three chaotic secret key sequences can be generated using 2D-STCM.

The next step of key generation is to create a chaotic sequence by executing the 2D-STCM. The paper employed a 2D chaotic map to overcome the boundaries of the one-dimensional chaotic maps [47–48]. A 2D-STCM is described as:

^x n+1

f((sin(?ryn) + 3) * xn/2) mod, 1,       xt < 0.5

[ ((sin(^yn) + 3) * (1 - xn)/2)mod 1,xt > 0.5

Уп+1 =

Г((sin(^xn+1) + 3) * yn/2) mod 1,       y; < 0.5

[ ((sin(TTxn+1) + 3) * (1 - yn)/2)mod 1,y; > 0.5

are inputted into the chaotic map function. Accordingly, three chaotic key sequences will be generated for each set of inputted values. The sequences generated through the above function are non-periodical and much sensitive to the initial conditions.

To get a secure key sequence, zigzag scanning method is applied to the chaotic sequence produced in the previous

The set of initial values ( x , y ) got in the previous step

(a)

(b)

Fig.1. Conjugate Transcendental Fractal Images using Iteration Method (a) Picard; (b) Mann; (c) Ishikawa

(c)

0	1	2	3
4	5	6	7
8	9	10	11
12	13	14	15

0    1    2    3    4    5    6    7    8    9    10    11    12    13    14    15

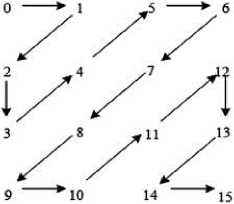
Fig.2. Zigzag Scan Method

Step. The zigzag scanning method helps to minimize the correlation coefficient value of adjacent pixels by tracing the elements of a matrix in a particular sequence. The method starts with the scanning of a 2D matrix and produced a definite sequence of elements in a 1D form [49]. The fig. 2 depicts the used zigzag scanning approach.

• B.    The Encryption Method

This section discussed the anticipated encryption algorithm implemented for the color images and the gray images. The method diffused the plain image by using a security key in single phase. The detailed description is as Step 2(b): follows:

Step 1: Process starts by inputting a plain image PI of size M*N to be encrypted and a set of values ( x0 , n , s , s’ ) to be keyed in the fractal function.       Step 2(c):

Key Generation Process:

Step 2(d): Step 2(a):   Step 2(a): Using the set of values (x0, n, s, s’), iterates the conjugate transcendental fractal function (refers eq. (5)) and get three sets of preliminary values (x, y) by iterating it using Picard, Mann and Ishikawa iteration methods. The value of constant variable s and s’ is 0.5 and 0.8 respectively and complex value c used in each iteration is (0.025, 0.0125), (-0.296875, 0.78125), and (0.6, -0.025) which are obtained by implementing the fractal function using UltraFractalTM software. The initial values obtained through this method are nothing, but the fixed point of the CTFF obtained after repeating the same operation for definite times.

Pass each set of preliminary values ( x , y ) and the dimensions of the input image (M*N) to the 2D-STCM function (refer eq. (6 & 7)) three times and obtained chaotic key sequences accordingly ( S 1, S 2, S 3).

Apply zigzag scanning to each sequence separately and got one-dimensional three scanned chaotic sequences resultantly.

Convert each chaotic sequence into twodimensional (M*N) form and XORed all sequences to get the security key SK of size M*N.

Encryption Process:

Step 3(a):	Start the encryption process by summing the plain image pixel values as:
	PI^um = Y,^PIi	(8)
Step 3(b):	Start with i ^ 1, calculate:
	PIsum = PIsum - PI(i)	(9)

Temp = f loor (mod(PI sum * SK(i) * 2 2⁵⁶ ,256)) (10)

Here mod() function helps to maintain the value range between 0 and 255 and give the nearest integer value as the resultant because of the use of a floor() function. The variable Temp is calculated on each iteration using the current key value and a new calculated pixel sum value i.e. PIsum.

PIsum variable consists of the sum of pixel values, starts from second to last and gradually it becomes zero after each iteration.

Step 3(c):  If (i=1), then start encryption with the first pixel of the input image by XORing it with first security key value and Temp according to the given equation:

CI(i) = PI(i) ф SK(i) ф mod(Temp + var, 256) (11)

Step 3(d): Otherwise, use ith security key value and previously enciphered CI(CIi-1) to encrypt the ith  plain image pixel. Also, the new calculated Temp value is used to encrypt the corresponding pixel. The formula will be:

TempCI = mod(SK(i) + CI(i - 1), 256)   (12)

CI(i) = PI(i) ф TempCI ф Temp     (13)

Note that the value Temp changed on each iteration. Hence, contribute differently towards the cipher image computation.

Step 4: Increment i ^ i + 1 , go to step 3(b) and continue the process till i reaches to M*N.

Step 5: At last, we will have an array of encrypted values CI = {CI 1 , CI 2 , …, CI M*N }. Reshape the CI values into two-dimensional array and that will be our required encrypted image.

• C.    The Decryption Method

Generally, the decryption method is the inverse process of the encryption method except few initial steps. The decryption process starts with the security key which can be generated by using the accurate input values at the receiver end. The detailed process can be defined as:

Step 1: Generate the security key sequence SK by using the given set of values (x0, n, s, s’).

Step 2: Scan the cipher image and arrange image pixels in one-dimensional array as CI = {CI1, CI2,…, CIM*N}.

Step 3: Step 3: Start the decryption process by applying the encryption process in reverse from the last pixel of a cipher image. Set Temp ← 0, i ← M*N, and PIsum ← 0 (after completion of the encryption process, the value of PIsum will be zero). Compute the following steps:

TempPI = mod(SK(i) + CI(i - 1), 256)

PI(i) = CI(i) ф TempPI ф Temp(15)

PIsum = PIsum + PI(i)

Temp = floor(mod(PIsum * Sk(i - 1) * 2 ²⁵⁶ ,256))

Step 4: Decrement i ^ i — 1, go to step 3 and continue the process till i reaches to 2.

Step 5: Till the previous step execution, the complete cipher image will convert to original input image except its first pixel. Now to decrypt that pixel of cipher image, execute the given formula:

PI(i) = CI(i) ф SK(i) ф mod(Temp - var, 256) (18)

After execution, we will get a sequence of pixels in one-dimensional array which has to be reshaped into a two-dimensional array to get the plain image.

A system block diagram of key generation is given in fig. 3.

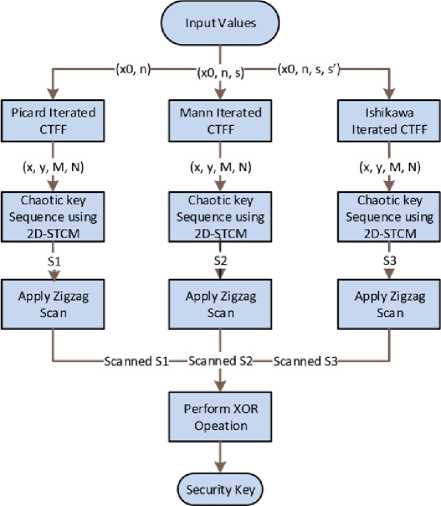
Fig.3. Key Generation Process Diagram

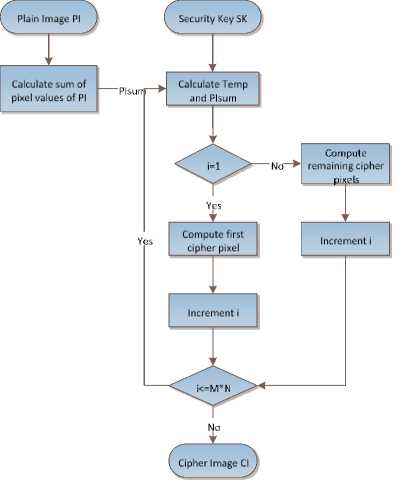
Fig.4. The Proposed Cryptosystem

A plain image PI is the original image which is supposed to be converted to cipher image CI. The above given diagram in fig. 4 shows the various steps used in the proposed cryptosystem design.

• IV. Performance and Security Analysis

  The above discussed encryption algorithm applied to the gray image and the color image of size 256*256. The set of values used to generate key stream is x 0=0.0, n =100, s =0.5 and s ’=0.8 and the variable ‘var’ is chosen as 10. The method is implemented using MATLAB^TM software with system configuration Intel® Atom™ x7-z8700 CPU @1.60 GHz and 4 GB RAM to measure the performance. Further, the simulation results and the performance of the algorithm given in terms of various measures.

• A.    Simulation Results

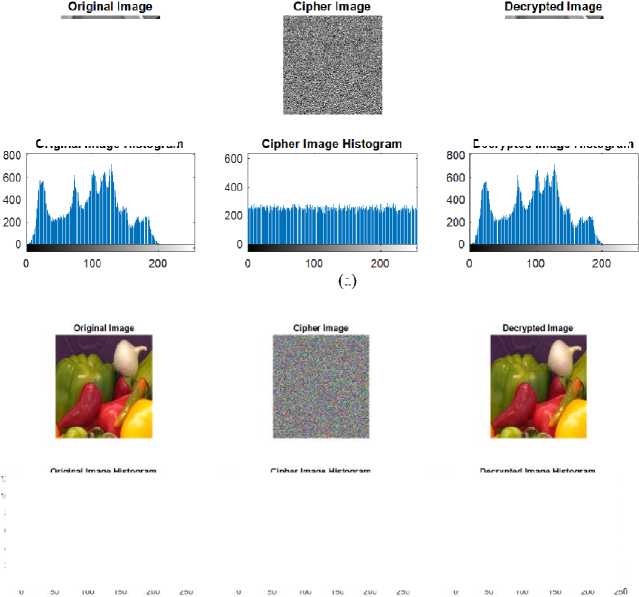
Fig. 5 displays the simulation result of applying the given algorithm to encrypt/decrypt the gray image and color image. The simulation result shows the encrypted image looks like a noisy image, in which pixels are randomly distributed throughout the image. The histogram of the Lena and peppers images and their corresponding encrypted images is also shown in the same figure. A histogram of an image refers to the image pixel distribution at each intensity level. The outcome shows that all plain images have a specific pattern in histogram whereas in cipher image, histogram distributed uniformly. It makes difficult to guess the original image by looking only at the cipher image histogram.

• B.    Computational Time Analysis

The encryption speed depends on various factors such as CPU, RAM size, compiler, and operating system, etc. A speed analysis is given for a test image of size 256*256

after conducting the complete process. The method implementation consists of two major parts: 1) key generation, 2) encryption/decryption. A key sequence is generated by performing the three steps (use of fractal function, chaotic map and zigzag scan), despite that the total time taken by the process is much less i.e. 0.107006s to 0.162707s. It proves that the use of fractal function in the key generation process does not require much time to execute. The estimated time to encrypt/decrypt the gray image and color image of size 256*256 was 1.367196s and 3.8807s respectively. The table 1 shows the execution time needed by the proposed method and other image encryption schemes.

• C.    Key Space Analysis

  To secure a cryptosystem from the brute-force attack, a key space must be greater 2¹⁰⁰ [50]. A key sequence in the given method is produced by inputting a set of values ( x 0, n , s , s ’) to the fractal function. If the used programming language complies with the IEEE floating point standard [51], the variables will be stored in the double data type. The memory space needed to accumulate a single parameter is 8 bytes with the computational precision about 10^-15. In that case, the possible secret key space will be 10^-15 *10^-15*10^-15*10^-15 ≈ 2²⁰⁰, which is quite enough to resists the brute-force attack.

• D.    Entropy Analysis

  Entropy analysis is a statistical measure of the predictability of randomness and unpredictability of an information source given by Shannon in 1949 [52]. The entropy E(s) of the source can be defined as:

E(s) = -T.^1P(si)log2P(si) (19)

Here P(s / ) is the expected occurance frequency of an image pixel si and depicted in bits. To compute entropy, the number of occurrences of symbol si with its probability of occurrence in cipher image is computed. The results in table 2 shows the entropy value of cipher image and the entropy values of other image encryption methods. As can be seen that the proposed scheme is having the resultant value 7.9989 (color image) i.e. nearby to the standard value 8. It proves that the cipher image has high randomness so secure from the entropy attack.

• E.    NPCR and UACI Analysis

The impact of the differential attack on the cryptosystem is necessary by observing, how a change in input affects the corresponding outcome. The number of pixel change rate (NPCR) and unified averaged changed intensity (UACI) are standardized test to analyze the strength of the proposed encryption scheme [53]. NPCR measures the influence of the change in plain image pixel to the corresponding cipher image. Consider two plain images “P1” and “P2” with one-pixel change and their corresponding encrypted images “C1” and “C2” respectively, then the NPCR can be defined as:

NPCR = ^E^iZV=i d(iJ) * 100%

Where, d will be calculated as:

f0,    if C1(W = C2(i,])

U(t,V)   {1,     if C1(ij) * C2(ij)      ()

A significantly high NPCR result considered as much sensitive to the change in an image pixel, hence strong resistance against differential attack. Considering the fact that, no two random images can be completely different, the maximum expected NPCR value is assumed to be 255/256 = 99.6093%.

UACI test computes the average intensity difference between C1 and C2 and is defined as:

U AC I = — ZM £« ^ci(l -ⁿ- ^C2(l -ⁿ * 100%   (22)

MiV  I=i 7 = i     255                   v '

The experimental values of NPCR and UACI are 99.5920% and 33.4446% respectively, quite close to the theoretical values. Table 3 compares the obtained results of the implemented algorithm with the other five methods. Therefore, the proposed scheme results are closest to the average NPCR and UACI scores to the expected ones.

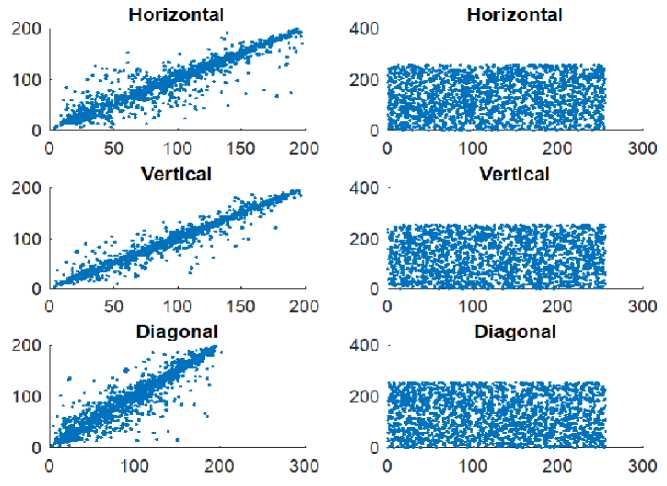
• F.    Adjacent Pixels Correlation

An image always possesses the high correlation within its adjacent pixels in horizontal, vertical and diagonal direction. The requirement of an efficient image encryption algorithm is to obtain such an encrypted image in which correlation between adjacent pixels must be equivalent to zero in all directions. To quantify the correlation factor, calculate the parameter using the given formula:

cov(x,y) CC =----- ox*^y

Where ax = ^var(x) and ay = ^var(y)

E(x)=1ZV=iXt var(x) = 1zV=i(x/ - E(x))2

cov ⁽ x,y) = ¹ Z ^V=i (x_/ - E ⁽ x))(y_t - E⁽y))

Fig 6 shows the implementation results by plotting pixel correlation in all directions (i.e. horizontal, vertical and diagonal). The visual testing proved that the strong correlated pixels in the original image are scattered uniformly in the encrypted image, hence greatly reduce the correlation between the pixels. Also, a table 4 shows the quantitative result of applying the proposed method along with other five methods. The values show the plain image pixels are strongly correlated to each other while it is quite weak in the cipher image. Therefore, the given method has successfully reduced the adjacent pixel correlation in all directions as needed.

(a)

(b)

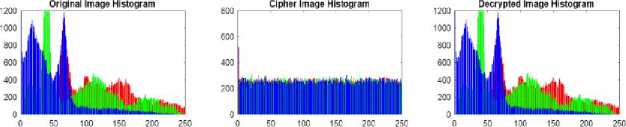
Fig.5. (a) Lena Original, Cipher and Decrypted Images with its Corresponding Histogram; (b) Peppers Original, Cipher and Decrypted Images with its Corresponding Histogram

Table 1. Execution Time Comparison (time unit: sec)

Method	Proposed Method	Ref. [18]	Ref. [19]	Ref. [40]	Ref. [20]	Ref. [21]
Processor Speed	1.60 GHz	2.40 GHz	2.40 GHz	2.40 GHz	2.0 GHz	3.1 Hz
Lena	1.367196	0.4	0.018	0.031	1.25	10.3959

Table 2. Information Entropy of Various Image Encryption Methods

Image Method	Lena	Cameraman	Baboon	Peppers
Plain Image	7.4139	7.0097	6.8178	7.6338
Proposed Algorithm	7.9970	7.9969	7.9989	7.9989
Ref. [18]	7.9980	7.9974	7.9973	7.9976
Ref. [19]	7.9973	-	7.9973	7.9975
Ref. [20]	7.9895	-	-	-
Ref. [21]	7.9993	-	7.9992	7.9992

• G.    Correlation Analysis between Plain and Cipher Image

A Correlation coefficient (CC) of two images represents the relationship between them that how much close/related to each other. The formula to compute CC is as:

сс =

(Z^^

JCzMU^j"^^              (27)

Where

A = ^1^=1^

and

¹ yM vN

^B = M _t N^Zl=1^Z j=1^B tj ^.

The variable A and B represents the plain image and cipher image respectively. Ideally the range of CC lies between -1 to +1. The value -1 depicts that the both images do not correlate to each other, whereas +1 depicts that the both images are close to each other. According to the given table 5, CC value of various images is close to zero, indicate that the both images are significantly different from each other.

• H.    Mean Square Error and Peak Signal-to-Noise Ratio Analysis

A mean square error value (MSE) indicates about how far the input image (P) pixels are from an encrypted image (C) pixels. The greater the MSE value, corresponds to the great difference between these two images. The formula to compute MSE is as:

MSE = ^^^(Р^у) - C(iJ)Y

A PSNR value is a standard way to compute the visual quality of encrypted image corresponding to its plain image. It is a ration between the maximum intensity of an image and MSE of that image. PSNR is calculated as:

PSNR = 20 log i ₀ [^^Ц]           (29)

Here I max is 255, the maximum image pixel value in which each pixel is represented using 8 bits. A low PSNR value implies high difference between a plain image and its corresponding encrypted image. See table 5 for the results. The comparison shows the better results of the implemented scheme than the other algorithm.

• I.    Key Sensitivity Analysis

A secure cryptosystem requires a large key space and a strong key sensitivity to the small change, otherwise an intruder might recreate the original image by guessing the security key. The previous section discussed about the available key space which proved adequate to the system requirement. Now the impact of key sensitivity to the encryption and the decryption quality of the proposed cryptosystem is examined.

A security key is generated by executing the CTFF using the complex variables z and c. To evaluate the key sensitivity, a slight change is made to the value of complex variable ‘c’ in each iteration and observed the behavior of encrypted and decrypted images. The set of changed values is:

• (1)    Case 1: Change only (0.6, -0.025) to (0.6001, -0.025) (2) Case 2: Change (-0.296875, 0.78125) and (0.6, -0.025) to (-0.296874, 0.78125) and (0.6001, -0.025)

  
  
  

  (a)

  
  

  (b)

  
  

Fig.6. (a) Correlation Distribution of Adjacent Pixels of Plain Image Horizontally, Vertically and Diagonally Respectively; (b) Correlation Distribution of Adjacent Pixels of Cipher Image Horizontally, Vertically and Diagonally Respectively

Table 3. Comparison of NPCR and UACI value of Different Image Encryption Methods

Method Parameter	Proposed Scheme	Ref. [18]	Ref. [28]	Ref. [40]	Ref. [20]	Ref. [21]
NPCR	99.5920	99.8023	99.65	99.62	99.7915	99.61
UACI	33.4446	33.5548	33.48	33.38	49.2191	33.40

Table 4. Correlation Coefficient Analysis of Two Adjacent Pixels in Cipher Image

Method	Correlation Coefficient
	Horizontal	Vertical	Diagonal
Plain Image	0.954125922	0.977809985	0.932092722
Proposed Scheme	0.002998127	0.002911998	-0.000473064
Ref. [18]	-0.00051014	-0.00576844	0.00029585
Ref. [28]	0.0020	-0.0007	-0.0014
Ref. [22]	0.0086	0.0014	0.0009
Ref. [20]	-0.00368	0.00014	-0.02298
Ref. [21]	0.009118	-0.027993	-0.008005

Image	Proposed Scheme			Ref. [18]
	CC	MSE	PSNR	CC	MSE	PSNR
Lena	-0.006285	8602.6	8.7845	0.00338909	9032	8.5731
Cameraman	0.001105	9388.4	8.4048	0.0014570	9415	8.3928
Baboon	-0.002226	12528	7.1519	-0.0007028	7385	9.4474
Peppers	0.000662	11287.7	7.60474	0.0023854	8261	8.9603

• (1)    Case 3: Change (-0.025,  0.0125),  ((-0.296875,

  0.78125), and (0.6, -0.025) to (-0.025001, 0.0125), ((-0.296874, 0.78125), and (0.6001, -0.025)

The resultant images are shown in fig. 7. Also, an additional test is executed to compare the pixels of two cipher images obtained using correct security key and modified security key. According to table 6 data, the NPCR and UACI values verified the sensitiveness of the given scheme in all three cases. Small change in the key value produces a great difference between the cipher images. So, an intruder will not be able to decrypt the cipher image even having an almost perfect key information.

• J.    Robustness to Data Loss and Noise

• V.  Conclusion

The paper is designed to utilize the characteristics of a fractal function and a chaotic map in the field of the image encryption. It is a symmetric key encryption method with a single round of the diffusion process.

In the proposed algorithm, a security key was generated by executing three steps which makes it difficult to guess by an intruder. A 2D chaotic map i.e. 2D-STCM used the initial values derived by iterating a conjugate transcendental fractal function (CTFF) to generate a chaotic key sequence. To decorrelate the adjacent image pixels, an additional step has been taken by performing zigzag scanning to the chaotic key sequence. In the first phase of cryptosystem design, the plain image is modified using diffusion process. Each original image pixel is encrypted using the corresponding security key pixel and the previously encrypted cipher image pixel. Through the experimental results, the effectiveness, correctness, security and robustness of the proposed method is verified. The following observations take place during the analysis process:

• •    The method possesses a larger key space to make brute-force attack infeasible.

• •    The uniform distribution of the pixels in the cipher image demonstrates the reduced correlation

between the adjacent pixels.

• •    Information entropy results indicate the value is close to the standard value 8, hence secure from entropy attack.

• •    All differential analysis measurements i.e. NPCR, UACI, MSE and PSNR proved the system is secure from differential attack and has a good encryption quality.

• •    The value of correlation coefficient is close to zero, indicates that the anticipated scheme works well to minimize the correlation after encrypting an original image.

• •    Key sensitivity also verified in the case of encryption and decryption using a slightly modified key. The results showed that the image transmission is secure from the unauthorized access.

• •    The above discussion verified the suitability of the proposed cryptosystem for image transmission over the unsecure network.

  

  (i)

  
  

Fig.7. Key Sensitivity Analysis of Gray and Color Image; (a) Plain Image; (b) Encrypted Image with Correct Key; (c) Decrypted image with Modified Key

Table 6. NPCR and UACI Values between Cipher Images

Change in Key Value	NPCR (%)	UACI (%)
Case 1	99.6124	33.5277
Case 2	99.6673	33.3514
Case 3	99.6322	33.5138

(ii)

Fig.8. Robustness of the Proposed Method against Data Loss and Noise for Gray and Color Image. (C1) The Cipher Image with 1% Speckle Noise; (C2) The Cipher Image with 2% Salt & Pepper Noise; (C3) The Cipher Image with 3.81% Data Loss; (C4) The Cipher Image with .01% Gaussian Noise; (D1), (D2), (D3), and (D4) are Corresponding Decrypted Images.