A Chaotic Lévy flight Approach in Bat and Firefly Algorithm for Gray level image Enhancement

Published Online June 2015 in MECS DOI: 10.5815/ijigsp.2015.07.08

The purpose of Image enhancement is to process an image using some transformation function such that the resultant image is more suitable than the original one for some specific applications [1]. Enhancement is taken as a pre-processing step in image processing field because many images, such as remote sensing images, medical images and also various real-life images suffer from poor contrast or the image is darker. In [31] pre-processing of fingerprint images helps to extract the features. Image enhancement can be applied for various image processing applications like contrast enhancement, noise reduction, edge enhancement and edge restoration. In this paper, contrast enhancement of gray level dark images taken into consideration. Not only gray level, color images can be also enhanced. Color images can be enhanced by separating the image into the chromaticity and intensity components [2,  3]. Histogram transformation is considered as one of the fundamental processes for contrast enhancement of gray level images [4, 29].

Histogram equalization (HE) is a mechanism that has no control over the rate of enhancement. The enhanced image always follows the uniform distribution. But the controlled enhancement is done by putting constraints on the probability density function with the bin underflow and bin overflow [5]. Although based on histogram information different techniques are proposed in literature but enhancement of dark and low contrast images in a controlled fashion is still a big problem. For this reason there is steady rise of soft computing oriented approaches. Recently natures inspired population based metaheuristics have been devised to solve optimization problems [7]. So, they can also apply in image processing field where some problems like image enhancement, segmentation etc has been considered as an optimization problems [8, 9, 10, 11]. Differential Evolution and Genetic Algorithm are stochastic and robust metaheuristics in the field of evolutionary computation and also used in image processing field to solve optimization problems [12, 10, 11, 30]. Mutation factor and crossover rate have been modified by chaotic sequence of traditional DE algorithm and experimental result shows that modified DE is far better than traditional DE in image enhancement field with fast convergence rate and maintain also a good diversity property [12]. Swarm optimization algorithms like Particle Swarm Optimization algorithm which are based on social behavior of organisms such as bird flocking and fish schooling are have been widely applied in image enhancement field to optimize the parameters of parameterized transformation function [2, 3, 13, 14]. PSO outperforms the GA in image enhancement field [2, 3]. PSO not only used for gray scale image enhancement but also used for color image enhancement where the intensity part of the colour image is separated from the chromaticity part and then apply the parameterized transformation function on the intensity part [3]. Newly developed another metaheuristic named ant colony optimization (ACO) is also applied in image enhancement technique and it gives better results than PSO and GA [15]. In this paper image enhancement has been taken as a non-linear optimization problem. Two new nature inspired metaheuristic algorithms are used to optimize the parameters named Bat Algorithm that based on the echolocation behavior of bats [17, 18] and Firefly algorithm that developed under inspiration of flashing behavior of fireflies [6, 7]. In both algorithm lévy flight has been played a great role. It controls the diversification as well as intensification in these algorithms. But the great disadvantage of lévy flight is to choose the proper value of step size. lévy flight with fixed step size does not show ergodicity property [19]. To remove this problem chaotic sequence has been used in both algorithms. It has been done because chaotic sequence has ergodicity property [20,  21]. Actually, chaotic sequence has been used in metaheuristic algorithms for the two purposes. One is to generate random numbers and another reason is to enhance the searching quality using chaotic search [16]. In evolutionary computation and swarm based computation chaotic sequence is used to enhance the capability of those algorithms [21, 22, 23]. In this paper it is used to generate random number. In this paper, low contrast images are enhanced using an algorithm that based on the principal of high boost filter. Chaotic lévy BA and chaotic lévy FA have been used to optimize the parameters. Experimental results show clearly that BA outperforms the FA.

• II.    T ransformation and O bjective F unction

• A.    Description of the proposed Algorithm

Actually this paper enhance the dark and low contrast images, so the algorithm much depend on the method of high-boost algorithm because pricipal applications of high-boost filtering is when the input image is darker than desired.by varying the boost coefficient, it generally is possible to obtain an overall increase in average gray level of thee image, thus helping to brighten the final result [1].

Maximum generation (MG) is 5.

Step 1: Compute

0i = «i + [а2хМ --% G+]

Step 2: For all pixel find the average or mean (m( i, j )) of its neighbourhoob pixels using [3 x 3]window.

Step 3: Modify all the pixels by

• * i (i, j ) = 0i x f(i , j ) + ⁽f⁽ i , j ) - m(i, j )) x 0₂

Step 4: IF ( f ( i, j ) < 0₃) then make f(i, ) = 0

Step 5: while(t ≤ MG), do step 1 to step 4

From the algorithm it is clear that pixel modifier function used in step 3 is nothing more than a high-boost filter. Functionality of step 4 in this algorithm is to help to maintain a good contrast. In this algorithm there are mainly four parameters, namely a_r , a ₂,0₂, 0₃.

• B.    Enhancement Criterion

The necessity of Objective function of optimization algorithms that used for image enhancement is to select a criterion that is associated to a fitness function which will say all about the image feature. In this paper three performance measurement parameters taken into account. These are Entropy, sum of the edge intensity and the number of edge pixels or edgels. It can be sure that good contrast enhanced image has more edgels and higher intensity of the edges [2]. If the allotment of the intensities is homogeneous, then histogram is equalized and the entropy of the image will be more. The objective function proposed in this paper is:

^(^)   ^9e     X (nedgeIsUe)/(MxN))xH(z) (1)

• ( ) is the fitness value of enhanced image, ( ) is

the sum of pixel intensities of Sobel edge image .

n_ed g _{e [s} y_e) is the number of edge-pixels whose intensity value is above a threshold in the Sobel edge image. Based on the histogram, entropy value ( ) is calculated on the enhanced image z. M , N is the number of row and column of the image respectively.

• C.    Lévy flight

Lévy Flight has been used to generate random walk which plays a great role in metaheuristic algorithms. A random walk is a mathematical method of representing a series of consecutive random steps. It has wide applications in the fields of computer science, physics, statistics, economics and engineering [7, 24]. It can be expressed by the formula

S_N = ^ i ^              (2)

Where, ^is a random step size drawn from a random distribution and is the sum of each of these consecutive random steps. Lévy Flight is a random walk whose step length is determined from the lévy distribution. It is capable of exploring large amount of search space. Lévy Flight is also found in nature as certain species of birds and insects exhibit this type of motion while gathering food [24]. Even physical phenomena such as diffusion of gas molecules have been seen to follow Lévy Flight behavior under the right conditions. Lévy Flight can be produced using different algorithms which include Rejection        algorithm, McCulloch’s algorithm,

Mantegna’s algorithm etc. In this study Mantegna’s algorithm has been used. It produces random numbers according to a symmetric Lévy stable distribution as described below— о = [Г(1 + a) sт(тш/2)/Г((1 + a)/2a2^)]5  (3)

Where, Г is the gamma function [24, 25], 0< a < 2 [24], in this study it is taken as 1.5 which is same as [25]. о is the standard deviation.

As per Mantegna’s algorithm the step length v can be calculated as,

" = 7|y|v .              ⁽⁴⁾

Here, x and y are taken from normal distribution and o_x = a, o_y = 1 [24]. Where a is the standard deviation. The resulting distribution has the same behavior of Lévy distribution for large values of the random variables [7, 25, 26]. Lévy Flight is used for the diversification as well as intensification in stochastic optimization algorithm [24, 25]. For the case of diversification the step length has been taken larger than in the case of intensification. The repetition of the same position in its space by lévy Flight is less than the Brownian motion [7, 24].

• D.    Chaotic Sequence

It has been proved that the cooperative behavior of ants and food collection behavior of bees and birds also shows chaotic behavior [16]. The complex behavior of nonlinear deterministic system is defined by chaos [20, 21]. Chaos has non-repetition property and for this it searches best solution faster than any searching strategy that depends upon the probability distribution [21]. It also has ergodicity property.

Recently, chaos combined with metaheuristic algorihms and produce good result [21, 22, 23]. Particle swarm Optimization (PSO) used chaotic sequence to increases the diversification property [21]. Evolutionary optimization algorithms can enhance its capability of searching global best solution using chaotic sequences [22].

There are several chaotic generators like logistic map, tent map, gauss map, sinusoidal iterator, lozi map, chua’s oscillator etc [22]. Among those simple logistic equation that based on logistic map is used in this paper to generate mutation factor. The equation of logistic map is given below:

L_m +. = aL _m (1-L_m)            (5)

a is a control parameter and 0< a < 4, is the chaotic value at m^th iteration. The behavior of the system is mostly depends on the variation of a . Value of a is 4 and L ₀ does not belong to {0, 0.25, 0.5, 0.75, 1} otherwise the logistic equation does not show chaotic behavior [12].

The range of L m is transformed to [0, 1] in this study.

Actually the power of all metaheuristic algorithms is depends on well combination of diversification or global exploration and intensification or local search. In those algorithms both these diversification and intensification have been done with the help of randomization. So it is clear that random number generators play a crucial role to increase the power of these types of algorithms. There is no theoretical proof that which random number generator is best for those algorithms and so all are experimental. In this study chaotic sequence and lévy flight have been taken into account.

• E.    Making of Initial Population

In population based algorithm some initial solutions have been generated. In this study randomization has been used to generate the initial population. Initially n numbers of individuals are generated using the equation given below:

Xi = low + (up - low) x d           (6)

Xi is the it individual. up & low are the upper and lower bound of the search space of objective function. d is the random variable belongs to [0,1]. If the initial solutions are generated in this way then the solutions diversely distribute [19]. In this paper, in the both algorithms d has been generated using chaotic sequence.

• III.    T heory of M etaheuristic A lgorithms

• A.    Bat Algorithm (BA)

One of the most efficient and rigid metaheuristic algorithm for solving computational problems is the BAT Algorithm.

Bat algorithm was originally presented by Xin She Yang under inspiration of echolocation behavior of bats [17, 18].

• B.    Idealize the behavior of Bats

There are three ideals rules which are assume for develop the algorithm. Rules are given below:

• 1)    All bats use echolocation to sense distance, and they also ‘know’ the difference between food/prey and background barriers in some magical way.

• 2)    Bats fly randomly with velocity Vi at position Xi with a fixed frequency fmin , varying wavelength λ and loudness A to search for prey. They can automatically adjust the wavelength (or frequency) of their emitted pulses and adjust the rate of pulse emission r ∈ [0, 1], depending on the proximity of their target.

• 3)    Although the loudness can vary in many ways, we assume that the loudness varies from a large (positive) A₀ to a minimum constant value A_{min .}[17]

• 4)    Pulse rate increase and loudness decrease when the bat going to reach to its prey.

• 5)    In general the frequency f in a range [ fmin, fmax ] corresponds to a range of wavelengths [ λmin, λmax ] [17].

• C.    Proposed Bat Algorithm

Bat algorithm composed of three phases. These are:

• 1)    In the first phase global search has been done. This global search technique is like particle swarm

optimization technique. Chaotic sequence has been played a crucial role in this stage.

• 2)    In the second phase local search or intensification has been done. This phase has been implemented with the help of the chaotic sequence.

• 3)    The last phase is like simulated annealing technique. This phase is an important one. In this phase the key idea is that always do not take the better solutions, sometimes takes some  bad

solutions with low probability so that it reduces the probability to trap in local minima. This simulated annealing technique in bat algorithm also maintains a good population diversity which restricts the premature convergence.

Another parameter which is called inertia weight is used in this study so that the algorithm does not take more time to converge at optimal or nearly optimal solution. Relatively large inertia weight has more global search ability while a relatively small inertia weight results in a faster convergence. In this paper inertia weight has been generated using chaotic sequence because it has ergodicity property. In [32] it is clear from experimental results that chaotic sequence can be a good inertia weight generator. The algorithm is given below:

Step 1: Objective function has been taken as per equation no. (1).

Step 2:   Initialize the population of bats,

X ={ xi | i=1,2,3,...,n }, where n is the number of bats or population size, and xi is the i^th bat.

Step 3: Initialise the Velocity ( V ), Frequency ( f ), Loudness ( A ) and Pulse rate ( r ) to each bat with the help of chaotic sequence.

Step 4: Generate new solutions by adjusting frequency using equations those are given below:

fi = fmm + Umax - fmm) X /?(7)

Vf = W* УГ1 + (Xf - X,) X ft(8)

Xf = X^1 + yf(9)

Here f_t controls the pace and range of the movement of every bat. X_tis the value of the parameter of enhanced image i, X , is the value of the parameter corresponding to current best enhanced image and f_t is the frequency of the bat or enhanced image i. w is the inertia weight generated using chaotic sequence within the range [0, 1].

Total step 4 is the global search part of the algorithm.

Step 5: For selection of best solutions Probability theory is used which is explain below. According to objective function f(x^) of X ; , probability value pi is

Pt = f it_t IX f it _t                  (10)

Where f itt is the fitness of the 11 h enhanced image and if      is greater than some threshold then the corresponding solution is belong to best solution

Step 6: if (rand > r_t) where rand e [0,1] Select corresponding best solution and create new solution using equation given below:

X_neWi = X_oшt + LmX sig n ⁽ rand - 0.5) x A_aug (11)

Otherwise, remains same Where, A _ayg is the average loudness of all bats, 6 is a random number belongs to [0, 1]

Total Step 6 is Local Search or intensification part of this algorithm.

Step 7:   if (rand < A _t &  f i t(X_t) < f i ((X , ) )

Accept solution that derived at local search part, Otherwise Accept solution that derived at global search part.

Step 7 is the Simulated Annealing (SA) part of this algorithm.

Step 8: As pulse rate increase and loudness decrease when bat going to reach to its prey,

So increase using

Ttnew =rt0, dx11-xpp^a))

Where, a =0.3, t is the current iteration number.

Decrease Ai using

Ai = A Xv(12)

mew Lold 5v

Where, v =0.9

Step 9: Rank the bats & find the current best X , .

Step 10: Repeat steps 4 to 9 equal to the maximum generation.

Step 11: Post process and visualize the result.

• D.    Firefly Algorithm

• a)    A Introduction

One of the most efficient and rigid metaheuristic algorithm for solving computational problems is the Firefly Algorithm [6, 7].

Firefly algorithm using Lévy flight was originally presented by Xin She Yang under inspiration of flashing behavior of fireflies [6].

• b)    Behaviour of fireflies

The model of flashes is often extraordinary for a specific species. The bursting of bright light is created by a method of bioluminescence, and the actual functions of such gestural systems are still in discussion. However, two fundamental functions of such flashes are to attract breeding partners (communication), and to evoke potential prey. The regular pattern of flash, the rate of flashing and the amount of duration form sector of the signal system that attracts both sexes together. Females reacts to a male’s creative sequence of flashing in the identical species, while in some categories such as photuris, female fireflies can replicate the mating flashing pattern of other division so as to tempt and eat the male fireflies who may mistake the flashes as a promising appropriate partner [6].

So, three flawless guideline of glowing behaviour of fireflies are:

• 1)    All fireflies are unisex so that one firefly will be allured to other fireflies regardless of their sex;

• 2)    Attractiveness proportional to their brightness, thus for any two glowing fireflies, the less bright one will be attracted towards the dazzling one. The attractiveness is proportional to the brightness and they both decrease as their interval amplifies. If there is no lustre one than a particular firefly, it will move haphazardly;

• 3)    The brightness of a firefly is determined by the landscape of the fitness function. In case of maximization problem, the brightness of firefly proportionally related to the value of the fitness function [6, 7].

In the firefly algorithm, there are two main issues: the difference of luminous intensity and production of the attractiveness [6, 7]. For a given medium with a fixed light absorption coefficient у , the light intensity I varies with the distance r . For this

I =   × exp(-yr)            (13)

Where, I is the original light intensity.

As a firefly’s attractiveness is proportionally related to the light intensity.

We can now define the attractiveness p of a firefly by p=   × exp(-yr2)           (14)

Pq is the attractiveness at r = 0.

• c)    Firefly Algorithm with Chaotic Lévy Flight

Begin

Take an objective function fit

Create initial population of enhanced images

Light intensity or fitness value I( of firefly or enhanced image x^ is determined by fit ( X^ )

Define light absorption coefficient

While ( t <= maximum generation)

For i = 1 to n all n enhanced images

For j = 1to n all n enhanced images

If ( Ij >  It )

Move firefly x_t towards Xj via lévy flight using chaotic step size

End if

Attractiveness varies with distance

Evaluate new solution and update light intensity or fitness value

End for j

End for i

Rank the enhanced images and select current best

End while

Post process results

End

In this algorithm, firefly x_t move towards Xj via lévy flight using the equation given below:

X[ =  + (V^i ( Xj - X[ )+ Ly^ SLQTL * rand - | + ⊗

Levy                                        (15)

a , Y are the randomization parameter, sign function gives the direction, rand is a random number within [0, 1], ⊗ is the entry-wise multiplication. Choosing of step length of lévy flight is very crucial. In the above algorithm chaotic sequence within the range [0, 0.5] has been used as step length because it has ergodicity property. Lin and Lee (2012) proposed to use chaotic sequence as the step size of lévy flight [27].

Distance ^rij measured between ^t and Xj using the equation given below:

Hi =√∑2.1( Xi ,;- Xj ,;)             (16)

Where, d is the dimension of the problem.

In this paper d =3, Po = 0․5, Y =0․5 for the traditional firefly algorithm.

• d)    D.C Parameter Selection

The Chaotic BA and FA are applied over have been applied over 100 images with initial population number being varied from 10 to 50 and maximum generations up to 100. In this study, numbers of initial populations have been put to 20, maximum generation for BA is 50, FA is 65 and PSO is 90.The result of FA, BA and PSO are very much parameter dependent. From the experiment value of the parameters are α1 ∈ [1, 2.5], α2 ∈ [0.2, 2], ∅₂ ∈ [0.05, 1] and ∅ 3 ∈ [5, 20].

• IV.    E xperimental R esults

  

  Fig. 1. Home original image

  
  

Fig. 2. Output of BA

Fig. 3. Output of FA

Fig. 4. Output of PSO

Fig. 5. Lady Original image

If the requirement is different then the methods are also different. In this study edge information has been taken into consideration. So, if the enhanced image is better than original one then the number of edge pixels increased. Sobel operator has been used to detect the edge of the image. The results has been given below:

Fig. 6. Output of BA

Fig. 7.Output of FA            Fig. 8. Output of PSO

Table 1.The number of edgels as detected with Sobel automatic edge detector

	Original Image	BA based	FA based	PSO based
Home	473	3151	2890	3065
Lady	1782	2302	1951	1922
Crown	511	2793	2267	2344

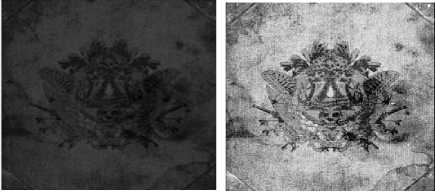
Fig. 9. Crown original image

2. Sum of the edge intensity pixels : Enhanced image has greater intensity value than original dark image. So if summation of intensity values of edge pixels is computed then it will be more than the original one. The numeric value of this metric has been given below:

Table 2. Sum of the edge intensity pixels

	Original Image	BA based	FA based	PSO based
Home	109.933	1634.1	1608.0	1652.60
Lady	632.526	1449.5	1056.2	1047.5
Crown	150.622	1740.6	1275.1	1149

Fig. 10. Output of BA

Fig. 11. Output of FA

3. Entropy: This metric tells about the information content of the image. If the histogram is equalized then the entropy of the image will be more. So if the enhanced image more equalized histogram then value of entropy will be more. The value of entropy is given below for different enhanced images.

Fig. 12. Output of PSO

A. Enhancement factor (EF)

EF is calculated using variance and mean of the image [28]. The Eq. is given below:

Table 3. Entropy of the images

	Original Image	BA based	FA based	PSO based
Home	5.803	7.528	7.577	6.9293
Lady	7.046	7.701	7.627	7.7064
Crown	5.649	7.812	7.604	7.5007

EF = ao

Mo

Fitness Value: Fitness value is increased if the output image is better than the original one. Actually in this study greater fitness means better enhanced image. The fitness values of different enhanced images of different techniques are given below:

Where,

mean of the enhanced image,

Sq = variance of the original image, =

mean of the original image

Now, the mathematical results have been shown below:

Four types of quality measurement metrics have been taken into account. These are:

1. Edgels: Actually this metric represents the number of edge pixels of the corresponding image. Image enhancement is done depends on the requirements.

Table 4. Fitness value of the images

	Original Image	BA based	FA based	PSO based
Home	0.1968	2.6780	2.4667	2.4014
Lady	1.2356	1.9689	1.5808	1.5718
Crown	0.2208	2.4843	1.8809	1.6956

B. Enhancement factor (EF)

EF is calculated using variance and mean of the image [28]. The Eq. is given below:

EF₌

°0

Mo

Where, ae = variance of the enhanced image,   = mean of the enhanced image,

°0 = variance of the original image, = mean of the original image

Enhanced images have greater variances than original images. So the value of enhancement factor is more for good enhanced image. The value of EF is given below:

Table 5. Enhancement Factor of the images

	BA based	FA based	PSO based
Home	6.032	5.176	4.564
Lady	6.153	5.431	3.969
Crown	5.877	4.095	3.672

• V.    Conclusion

In this paper image enhancement has been taken as an optimization problem. This optimization problem has been solved by using Bat algorithm, Firefly algorithm and Particle Swarm Optimization algorithm. In the Bat and Firefly algorithm chaotic sequence and lévy flight have been played a crucial role to control the diversification and intensification part of the of the both algorithms From the visual analysis and analytical results it is clear that chaotic BA outperforms the chaotic lévy FA and these two algorithms also outperforms the PSO algorithm in image enhancement field. So from experimental study it can be easily conclude that the nature inspired metaheuristics also play a crucial role to enhance the images. if the metaheuristic algorithm has been changed then the quality of enhanced image is changed. In future these algorithms can be modified so that its power can be increased and also applied in the field of image segmentation, denoising and many other field of image processing which can be considered as optimization problem.

This research work is funded by DST-PURSE.

• [1]    Gonzalez, R.C., Woods, R.E.: Digital Image Processing, 2nd edn. Prentice Hall, New York (2002)

• [2]    Gorai, A., Ghosh, A.: Gray-level Image Enhancement By Particle Swarm Optimization. In Proceedings of World Congress on Nature & Biologically Inspired Computing.( 2009)

• [3]    Gorai, A., Ghosh, A.: Hue preserving color Image Enhancement By Particle Swarm Optimization.IEEE,pp. 563-568,(2011)

• [4]    Garg, R., Mittal, B., Garg, S.:Histogram Equalization Techniques For Image Enhancement. International Journal of electronics    and communication

  technology.2,107-111(2011).

• [15]    Gupta, K., Gupta, A.: Image Enhancement using Ant Colony Optimization. IOSR Journal of VLSI and Signal Processing. 1, 38-(2012).

• [16]    Sheikholeslami, R., Kaveh, A.: A Survey of Chaos Embedded Meta-Heuristic Algorithms. Int. J. Optim. Civil. Eng. 3(4), 617-633 (2013).

• [17]    Yang, X.,  S.: A New Metaheuristic Bat-Insspired

  Algorithm. Nature Inspired Cooperative Strategies for Optimization, Studies in Computational Intelligence (Springer). pp- 65-74 (2010).