A Color-Texture Based Segmentation Method To Extract Object From Background

Published Online March 2013 in MECS

Color image segmentation is useful in many applications. From the segmentation results, it is possible to identify regions of interest and objects in the scene, which is very beneficial to the subsequent image analysis or annotation. Recent work includes a variety of techniques: for example, stochastic model based approaches [1], [2], [3], [4], [5], morphological watershed based region growing [6], energy diffusion [7], and graph partitioning [8]. Quantitative evaluation methods have also been suggested [9]. However, due to the difficult nature of the problem, there are few automatic algorithms that can work well on a large variety of data. The problem of segmentation is difficult because of image texture. If an image contains only homogeneous color regions, clustering methods in color space such as [10] are sufficient to handle the problem. In reality, natural scenes are rich in color and texture. It is difficult to identify image regions containing colortexture patterns.

Flowers in images are surrounded by a green or brown background and need to be segmented from the background. This paper presents new color and texture based method for segmenting flowers. The colored flowers are segmented from the background. Developing a system for segmentation of flowers is a difficult task. In real environment, images of flowers are often taken in natural outdoor scenes where the lighting condition varies with the weather and time. In addition, flowers are often more or less transparent and specula highlights can make the flower appear light or even white causing the illumination problem. In addition, there is lot more variation in viewpoint, occlusions, scale of flower images. All these problems lead to a confusion and make the task of flower segmentation more challenging. In addition, the background also makes the problem difficult, as a flower has to be segmented automatically.

Applications of segmentation of flowers can be found useful in floriculture, flower searching for patent analysis etc. The floriculture has become one of the important commercial trades in agriculture owing to steady increase in demand of flowers. Floriculture industry comprises of flower trade, nursery and potted plants, seed and bulb production, micro propagation and extraction of essential oil from flowers. In such cases, automation of flower segmentation is very essential. Flower segmentation can be used in flower recognition. Further, flower recognition is used for searching patent flower images to know whether the flower image applied for patent is already present in the patent image database or not [11]. Since these activities are being done manually and it is mainly labor dependent and hence automation is necessary.

Nilsback and Zisserman [12] proposed a two-step model to segment the flowers in color images, one to separate foreground and background and another model to extract the petal structure of the flower. This segmentation algorithm is tolerant to changes in viewpoint and petal deformation, and the method is applicable in general for any flower class. Das et al., [13] proposed an indexing method to index the patent images using the domain knowledge. The flower was segmented using iterative segmentation algorithm with the domain knowledge driven feedback. A threshold-based segmentation was proposed in [14].The paper in [15] presented a segmentation technique based on anisotropic diffusion, which is less complex. The colored flowers are segmented from the background. In this diffusion technique, the edge stopping function is computed as inversely proportional to the weighted sum of gradients of color components.

The present paper is organized as follows: section II deals with the basic concepts of mathematical morphology, section III introduces GLCM, section IV deals with OTSU thresholding, section V describes the proposed methodology, in section VI the experimental results are discussed and finally section VII deals with conclusions.

• II.    MATHEMATICAL MORPHOLOGY

  Mathematical morphology is a set theory approach, developed by J.Serra and G. Matheron. It provides an approach to processing of digital images that is based on geometrical shape. Two fundamental morphological operations – erosion and dilation are based on Minkowski operations. There are two different types of notations for these operations: Serra/Matheron notation and Haralick/Sternberg notation. In this paper Haralick/Sternberg notation, which is probably more often used in practical applications, is used. In this notation, erosion is defined as follows (Eq. 1) (Serra, 1982):

y e в and dilation (Eq. 2) as:

X e в = и Xy(2)

y e B

Xy = { x + y : x e X }(3)

where:

6 = { b :-b e B }(4)

Another important pair of morphological operations are opening and closing. They are defined in terms of dilation and erosion, by equations (5) and (6) respectively.

X о B = ( X & в ) ® B                    (5)

x • b = (X e B) 0B                        (6)

Morphological filling is another important operation used to fill holes in an image. Let ‘A’ denote a set whose elements are 8- connected boundaries, each boundary enclosing a background region i.e., a hole. Given a point in each hole, the objective is to fill all the holes with 1s.The initial array X0 is formed with 0s and 1s and is of same size as of ‘A’. The value ‘1’ in X0 corresponds to the given point in each hole. Filling operation is defined by equation (7) as where B is the structuring element. The algorithm terminates at iteration step k if Xk=Xk-1. The set Xk contains all the filled holes. The set union of Xk and A contains all the filled holes and their boundaries.

• III.    GLCM

Gray level co-occurrence matrix (GLCM) has been proven to be a very powerful tool for texture image segmentation [16, 17]. The only shortcoming of the

GLCM is its computational cost. Such restriction causes impractical implementation for pixel-by-pixel image processing. In the previous works, GLCM computational burden was reduced by two methods, at the computation architecture level and hardware level. D. A. Clausi et. al. restructures the GLCM by introducing a GLCLL (gray level co-occurrence linked list), which discard the zero value in the GLCM [18].This technique gives a good improvement because mostly GLCM is a sparse matrix where most of its values are equal to zeroes. Thus, the size of GLCLL is significantly smaller than GLCM. Then the structure of the GLCLL was improved in [19, 20]. Another work is presented in [21] where fast calculation of GLCM texture features relative to a window spanning an image in a raster manner was introduced. This technique was based on the fact that windows relative to adjacent pixels are mostly overlapping, thus the features related to the pixels inside the overlapping windows can be obtained by updating the early calculated values. In January 2007, S. Kiranyaz and M. Gabbouj proposed a novel indexing technique called Hierarchical Cellular Tree (HCT) to handle large data [22]. In his work, it was proved that the proposed technique is able to reduce the GLCM texture features computation burden.

B and B ˆ are structuring elements

V^ =^2р№,у) = т т у

GLCM is a matrix that describes the frequency of one gray level appearing in a specified spatial linear relationship with another gray level within the area of investigation [23]. Here, the co-occurrence matrix is computed based on two parameters, which are the relative distance between the pixel pair d measured in pixel number and their relative orientation φ. Normally, φ is quantized in four directions (0⁰, 45⁰,90⁰ and 135⁰) [23]. In practice, for each d, the resulting values for the four directions are averaged out. To show how the computation is done, for image I , let m represent the gray level of pixels (x, y) and n represent the gray level of pixels ( x±dɸ 0 , y±dɸ 1 ) with L level of gray tones where 0 ≤ x ≤ M -1, 0 ≤ y ≤ N -1 and 0 ≤ m, n ≤ L -1. From these representations, the gray level co-occurrence matrix Cm, n for distance d and direction ɸ can be defined as (8)

Where P {.} =1 if the argument is true and otherwise, P {.} =0. For each ɸ value, its ɸ0and ɸ1 values are referred as in the Table 1.

Table 1: Orientation constant

0	^0
0°	0	1
45°	-1	-1
90°	1	0
135°	1	-1

In the classical paper [24], Haralick et. al introduced fourteen textural features from the GLCM and then in [25] stated that only six of the textural features are considered to be the most relevant. Those textural features are Energy, Entropy, Contrast, Variance, Correlation and Inverse Difference Moment. Energy is also called Angular Second Moment (ASM) where it measures textural uniformity [23]. If an image is completely homogeneous, its energy will be maximum. Entropy is a measure, which is inversely correlated to energy. It measures the disorder or randomness of an image [23]. Next, contrast is a measure of local gray level variation of an image. This parameter takes low value for a smooth image and high value for a coarse image. On the other hand, inverse difference moment is a measure that takes a high value for a low contrast image. Thus, the parameter is more sensitive to the presence of the GLCM elements, which are nearer to the symmetry line C (m, m) [23]. Variance as the fifth parameter is a measure that is similar to the first order statistical variables called standard deviation [26]. The last parameter, correlation, measures the linear dependency among neighboring pixels. It gives a measure of abrupt pixel transitions in the image [27].

• IV.    OTSU thresholding

This method, as proposed by [25] is based on discriminate analysis. The threshold operation is regarded as the partitioning of the pixels of an image into two classes C0 and C1 (e.g., objects and background) at grey-level t, i.e., C0 = {0, 1, 2, t} and C1 = {t + 1, t +2,….L-1}. Let σ2w, σ2B and σ2T be the within-class variance, between-class variance, and the total variance, respectively. An optimal threshold can be determined by minimizing one of the following (equivalent) criterion functions with respect to

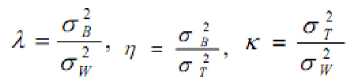
The optimal threshold t is defined as t= ArgMin η                                  (10)

£-lr                     £-lr i

<Г^ = EU-^rJ ^T = EM

I-U                     1»O                         (11)

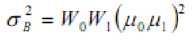
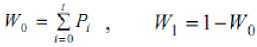
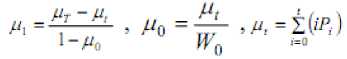
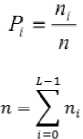
Moreover, P i is the probability of occurrence of greylevel i. For a selected threshold ‘t’ of a given image, the class probabilities w 0 and w 1 indicate the portions of the areas occupied by the classes C 0 and C 1 . The class means µ 0 and µ 1 serve as estimates of the mean levels of the classes in the original grey-level image. Moreover, the maximum value of η, denoted by η*, can be used as a measure to evaluate the separability of classes C₀ and C₁ in the original image or the bimodality of the histogram. This is a very significant measure because it is invariant under affine transformations of the greylevel scale. It is uniquely determined within the range 0≤ η≤1.The lower bound (zero) is obtained when and only when a given image has a single constant grey level, and the upper bound (unity) is obtained when and only when two-valued images are given.

• V.    METHODOLOGY

In the first step RGB image is converted to Lab color space. Lab color space is a three-dimensional space map based on the composition of chroma and luminance. In this model L denotes the luminance, a and b components represents the chroma value. The solution to convert digital images from the RGB space to the L*a*b* color space which had been mentioned below in the following formula

L*=116f(Y/Yn)-16 a*=500[f(X/Xn)-f(Y/Yn)] b*=200[f(Y/Yn)-f (Z/Zn)]

• X, Y, Z, Xn, Yn, and Zn are the coordinates of CIEXYZ color space. The solution to convert digital images from the RGB space to the CIEXYZ color space is as the following formula

  X		0.608 0.174 0.201	R
  Y	=	0.299 0.587 0.114	G             (18)
  Z		0.000 0.068  1.117	B

Xn, Yn, and Zn are respectively corresponding to the white value of the parameter.

x⅓              x>0.008856

f(x) = 1 7.787 x + 16/116    x<=0.008856         (19)

Each color space has its own appear background and application region. When segmenting a color image, the selection of color space plays a decisive role on the segmentation results. The common color spaces used in color image processing include RGB color space, HSI color space, Lab color space, and so on. At present, the general color digital images are RGB format. RGB color space is based on the theory of three-basic color to build. RGB format is the most basic color space. Other color space models can be obtained through the RGB format conversion. But the RGB color space is not a homogeneous visual perception space, it is not conducive to image segmentation based on color feature. HSI color space uses color characteristics of a direct sense of the three quantities: the brightness or lightness (I), hue (H), saturation (S) to describe the color. This method is more in line with the human eye habits to the description of the color, but the expressed colors are incomplete visual perceived color. The Lab color space is a homogeneous space for visual perception, the difference between two points in the Lab color space is same with the human visual system. It applies to represent and calculate of all light color or object color, so the Lab color space is very effective in color image analysis.

The ‘a’ component is extracted from the transformed Lab color space in the second step. The positive direction of a-axis represents the red color’s changes and the negative direction of a-axis represents the green color’s changes. The ’a’ channel is selected in order to eliminate the green leaves and to extract the flowers. In the third step the extracted a- component is subjected to OTSU thresholding. The two-dimensional OTSU algorithm automatically selects the optimal threshold for segmentation. Because two-dimensional OTSU algorithm not only takes into account the grayscale information of pixels, but also considers the space-related information of pixels and their neighborhoods. GLCM is obtained for the otsu thresholded image. For each image and with distance set to one, four GLCMs having directions 0°, 45°, 90° and 135° are generated. The co-occurrence matrix is often correlated with the directions. The directions of flowers are random. Therefore, it is difficult to describe precisely the texture feature for a flower image simply with one-direction of co-occurrence matrix. It is necessary to select more than one direction of gray level co-occurrence matrix for a comprehensive statistical processing. The synthetic gray level co-occurrence matrix of an image can be got by averaging the values of energy matrices in 0 degree, 45 degree, 90 degree and 135 degree. In the fifth step morphological filling operation is performed in order to fill small holes. A hole is defined as an area of dark pixels surrounded by lighter pixels or may be defined as a background region surrounded by a connected border of foreground pixels. This process can be used to make objects in an image seem to disappear as they are replaced with values that blend in with the background area. This function is useful for image editing, including removal of extraneous details or artifacts. As last step morphological opening operation is performed to remove small objects.

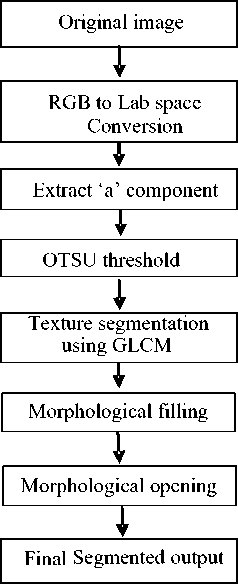
Figure 1. Flowchart of Proposed algorithm

• VI.    RESULTS

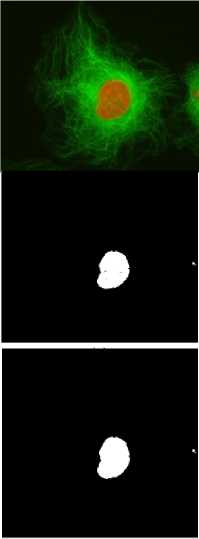
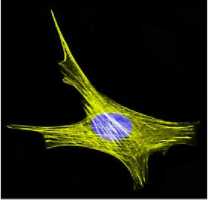
The proposed algorithm is tested on flower texture images of plague database. In this paper step wise results of flower images and medical images are shown in Figs.2-5. The results in Figs.2-3 clearly show the extraction of flower from the background. The algorithm is also tested on medical images for the extraction of nucleus in actin images and the results are shown in Figs.4-5. Actin images are collected from [28]. The results clearly indicate that the green and yellow backgrounds in the images are converted to black in the ‘a’ component of the image. Otsu threshold is applied for enhancing the ‘a’ component output. The Figs.2-5 (d) shows that the object is smoothened after texture segmentation. The Figs.2-5 (e) clearly shows that morphological filling step is applied to fill small gaps in the object. To remove small objects morphological opening step is applied as shown in Figs .2-5 (f). The results of the above algorithm applied on the medical images show that the algorithm can be used for nucleus extraction as shown in Figs 4-5.

Figure 3. flower image segmentation stepwise results of proposed algorithm. (a) Original image (b) ‘a’ component (c) OTSU thresholded (d) GLCM output (e) morphological filling (f) opening

(a)

(c)

(e)

Figure 2. flower image segmentation stepwise results of proposed algorithm. (a) Original image (b) ‘a’ component (c) OTSU thresholded (d) GLCM output (e) morphological filling (f) opening

(e)

Figure 4. nucleus segmentation stepwise results of proposed algorithm. (a) Original image (b) ‘a’ component (c) OTSU thresholded (d) GLCM output (e) morphological filling (f) opening

(d)

(f)

(c)                                     (d)

(a)

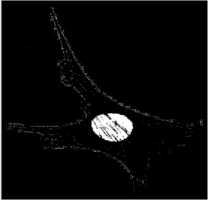
(b)

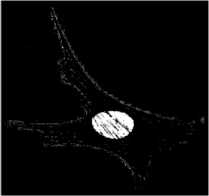
(c)

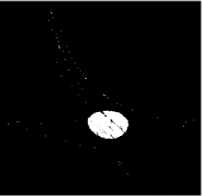
(d)

(e)

(f)

Figure 5. nucleus segmentation stepwise results of proposed algorithm. (a) Original image (b) ‘a’ component (c) OTSU thresholded (d) GLCM output (e) morphological filling (f) opening

• VII.    Conclusion

The information, which the commonly used grayscale images contain, is not enough for flower segmentation. When flower images are collected in nature, the background is generally more complex and more close to the target color, so there are some limitations in these conditions if we only use gray level information. However, the color images are able to provide more information. There are colors and color depth information, in addition to its provision of brightness and color images can be expressed by a variety of color space. Therefore, segmentation based on color image can overcome some shortcomings of gray-scale image. In this algorithm both color and texture features are considered. In this method, segmentation speed is faster and without human participation, the segmentation result is also ideal. The results show the efficiency of the above algorithm.

Acknowledgment

The authors would like to express their gratitude to Sri K.V.V. Satya Narayana Raju, Chairman, and K. Sashi Kiran Varma, Managing Director, Chaitanya group of Institutions for providing necessary infrastructure. Authors would like to thank anonymous reviewers for their valuable comments and SRRF members for their invaluable help. The authors would like to express their gratitude to Dr.G.Tulsi Ram Das, Vice chancellor, JNTU Kakinada.