A Common Fixed Point Theorem for R-Weakly Commuting Maps Satisfying Property (E.A.) in Fuzzy Metric Spaces Using Implicit Relation

• I.   Introduction

  In 1986, Jungck [3] introduced the notion of compatible maps for a pair of self mappings. However, the study of common fixed points of non-compatible maps is also very interesting. Aamri and El. Moutawakil [1] generalized the concept of noncompatibility by defining the notion of property ( E.A ) and in 2005, Liu, Wu and Li [2] defined common ( E.A ) property in metric spaces and proved common fixed point theorems under strict contractive conditions. Jungck and Rhoades [4] initiated the study of weakly compatible maps in metric space and showed that every pair of compatible maps is weakly compatible but reverse is not true. In the literature, many results have been proved for contraction maps satisfying property

( E.A .) in different settings such as probabilistic metric spaces [5, 6]; fuzzy metric spaces [7, 8, 9, 10, 11].

In this paper, employing the common ( E.A ) property, we prove a common fixed theorem for R -weakly commuting mappings via an implicit relation in fuzzy metric space.

• II.   Preliminaries

Definition 2.1. [12] A binary operation * : [0,1]×[0,1] → [0,1] is continuous t -norm if * satisfies the following conditions:

• (i)    * is commutative and associative;

• (ii)    * is continuous;

• (iii)    a * 1 = a for all a ∈ [0,1];

• (iv)    a * b ≤ c * d whenever a ≤ c and b ≤ d for all a , b , c , d ∈ [0,1].

Kramosil I and Michalek J.[13] introduced the concept of fuzzy metric spaces as follows:

Definition 2.2[13] : The 3-tuple (X, M, *) is called a fuzzy metric space (shortly, FM-space) if X is an arbitrary set, * is a continuous t -norm and M is a fuzzy set in X x [0, ^) satisfying the following conditions:

(FM-1) M(x, y, 0) = 0 ,

(FM-2) m( x , y, t) = 1 , for all t >  0 if and only if x = y , (FM-3) M(x, y, t) = M(y, x, t),

(FM-4) M(x, y, t) * M(y, z, s) ≤ M(x, z, t + s) (Triangular inequality) and

(FM-5) M(x, y, .) : [0, 1) → [0, 1] is left continuous for all x , y , z е X and s , t >  0 .

Note that M(x, y, t) can be thought of as the degree of nearness between x and y with respect to t .

We can fuzzify examples of metric spaces into fuzzy metric spaces in a natural way:

Let (X, d) be a metric space. Define a * b = a + b for all a, b in X. Define M(x, y, t) = t /(t + d(x, y)) for all x, y in X and t > 0 .Then (X, M, *) is a fuzzy metric space and this fuzzy metric induced by a metric d is called the Standard fuzzy metric.

Consider M to be a fuzzy metric space with the following condition:

(FM-6) lim_t ^^ M(x, y, t) = 1 for all x, y in X and t >  0 .

Definition 2.3[13]: Let (X, M, *) be fuzzy metric space. Then

• (a)    a sequence { x } in X is said to be c auchy sequence if, for all t >  0 and p >  0 ,

lim M(xn + p , xn , t) = 1 n ^W       r and

• (b)    a sequence { x } in X is said to be convergent to

• a point x е X if, for all t >  0 ,

lim M ( x , x , t ) = 1 .

n ^W

Definition 2.4[13]: A fuzzy metric space (X, M, *) is said to be complete if and only if every Cauchy sequence in X is convergent.

Example 2.1[13]: Let X = { 1 n • n е N } o { 0 } and let * be the continuous t-norm and defined by a * b = ab for all a , b е [0,1] . For each t >  0 and x , y е X , define M, by

t

M ( x , y , t ) = J t+|x-y|,

t > 0,

t=0

Clearly, (X, M, *) is complete fuzzy metric space.

Definition 2.5[11]: A pair of self mappings ( A, S ) of a fuzzy metric space (X, M, *) is said to be commuting if

M( ASx, SAx, t) = 1 for all x е X .

Definition 2.6[11]: A pair of self mappings ( A, S ) of a fuzzy metric space (X, M, *) is said to be weakly commuting if M( ASx , SAx , t ) ≥ M(Ax, Sx, t) for all x е X and t > 0 .

Definition 2.7[11]: A pair of self mappings ( A, S ) of a fuzzy metric space (X, M, *) is said to be compatible if lim n→∞ M(ASx n , SAx n , t) = 1 for all t > 0, whenever { x n } is a sequence in X such that lim n→∞ Ax n = lim n→∞ Sx n = u for some u in X .

Definition 2.8[10]: Let (X, M, *) be a fuzzy metric space. A and S be self maps on X. A point x in X is called a coincidence point of A and S iff Ax = Sx . In this case, w = Ax = Sx is called a point of coincidence of A and S .

Definition 2.9[10]: A pair of self mappings ( A, S ) of a fuzzy metric space (X, M, *) is said to be weakly compatible if they commute at the coincidence points i.e., if Au = Su for some u е X , then ASu = SAu.

It is easy to see that two compatible maps are weakly compatible but converse is not true.

Definition 2.10 [1]: A pair of self mappings ( A, S ) of a fuzzy metric space (X, M, *) is said to satisfy the property ( E.A ) if there exist a sequence { x } in X such that lim Ax_n = lim Sx_n = z for some z е X .

Example 2.2[1]: Let X =[0,∞). Consider (X, M, *) be a fuzzy metric space as in Example 2.1.

Define A, S : X →X by Ax = and Sx = for all

(C) ф ( u , u ,1,1) >  0 ^ u >  1

x G X . Clearly, for sequence

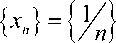
, A and S satisfies property (E.A).

Definition 2.11 [2]: Two pairs ( A, S ) and ( B, T ) of self mappings of a fuzzy metric space (X, M, *) are said to satisfy the common ( E.A ) property if there exist two sequences { x } and { y } in X such that lim Ax = lim Sx = lim By = lim Ty_n = z n ^to         n ^to        n ^to         n ^to

Example 3.1: Define ф : [ 0,1 ] ^ R as ф ( t_x , t ₂, t ₃, t ₄ ) = 14 t_x - 12 t ₂ + 6 t ₃ - 8 t ₄ . Clearly, ф satisfies all conditions (A), (B) and (C). Therefore, ф G M₄ .

We begin with following observation:

Lemma 3.1: Let { A } , S and T be self mappings of a fuzzy metric space (X, M, *) satisfying the following:

for some z G X .

• (3.1)    the pair ( A , T ) satisfies the E.A. property;

Example 2.3[2]: Let X = [-1, 1]. Consider (X, M, *) be a fuzzy metric space as in Example 2.1. Define self mappings A, B, S and T on X as Ax = x/ 3, Bx = - xj 3, Sx = x, Tx = - x for all x G X . Then, with sequences {xn}={1^} and

• (3.2)    for any x, y in X, ф in M₄ and and for all t >  0 there exists k G (0,1) such that,

  ^ф

  
  

^ M ( Ax , Ay , kt ), M ( Sx , Ty , t ),^л _v M ( Sx , Ax , t ), M(Ty , A_oy , kt ) _v

> 0;

{ ^yn H К ^}

in X, one can easily verify that

• (3.3)    A ( X ) c T ( X ) or A ( X ) c S ( X ).

lim Ax_n = lim Sx„ = lim By„ = lim Tv = 0

n ^to         n ^to        n ^to         n ^to

Therefore, pairs ( A, S ) and ( B, T ) satisfies the common ( E.A .) property.

Definition 2.12[11]: A pair of self mappings ( A, S ) of a fuzzy metric space (X, M, *) is said to be R -weakly commuting if there exist R > 0 such that

M ( ASu , SAu , t ) >  M ( Au , Su , t/R ) .

• III.    Main Results

Implicit relations play important role in establishing of common fixed point results.

Let M4 be the set of all real continuous functions ф: [0,1] ^ R, non-decreasing in the first argument and satisfying the following conditions:

• (A)    ф ( u ,1, u ,1) >  0 ^ u >  1,

• (B)    ф ( u , 1,1, u ) >  0 ^ u >  1

t hen the pairs ( A , S ) and ( A , T ) share the common (E.A.) property.

Proof: a s the pair ( A , T ) satisfies e.a. property, then there exist a sequence { x } in x such that lim Ax_n = lim Tx_n = z for some z G X . Since n ^to          n ^to

A (X) c S(X), hence       for each {xn }, there exist {yn} in X such that Axn = Syn . Therefore, lim Axn = lim Syn = lim Txn = z . Now, we claim n ^to         n ^to       n ^to that lim A y = z . in n ^to

Suppose that  lim Axyn ^ z , then applying n ^to inequality (3.2), we obtain

ф

^{Л M} ( a-У п , A 0 x n , ^kt ), ^M ( Sy n , ^Tx n , t ), Y ₀ V ^{M (} &У п , Aiy n , t ), ^{M (T}x n , A 0 x n , ^kt ) j”

which on making n ^ да reduces to

( M (lim Ay , z , kt ), M ( z , z , t ), )

n ^да

M (lim Ay , z , t ), M ( z , z , kt )

\     n ^да                           /

As ф is non-decreasing in the first argument, we have f M (lim Ay, z, t ),1,)

n ^да

Ф

M (lim Ay n , z , t ),1 \     n ^да

> 0

Using (B), we get M (lim Ay , z , t ) >  1 . Hence n ^да

M (lim Ay , z , t ) = 1 . Therefore, lim Ay = z .

n ^да                                   n ^да hence, the pairs (A, S) and (A, T) share the common (E.A.) property.

Theorem 3.1: Let { A }, S and Tbe self mappings of a fuzzy metric space (X, M, *) satisfying the conditions (3.1), (3.2), (3.3) of lemma 3.1 and the pairs (A, S) and (A, T) are R-weakly commuting. if range of one of S and T is closed subspace of X then

{ A } , S and T have a unique common fixed point.

Proof: By lemma 3.1, the pairs (At,S) and (A, T) share the common (E.A.) property, i.e. there exist two sequences {x } and {y } in X such that lim Ax = lim Sx = lim By = lim Tyn = z for n ^да n ^да n ^да n ^да some z G X . Suppose that S(X) is a closed subset of X, therefore, there exists a point u G X such that z = Su. We claim that Aiu = z. If Aiu ≠ z, then by (3.2), take x = u, y = xn ,

Ф

^z M ( A i u , A 0 x_n , kt ), M ( Su , Tx_n , t ), ' _v M ( Su , A i u , t ), M (Tx_n , A 0 x_n , kt ) _v

> 0

n > да

( M ( Au , z , kt ), M ( z , z , t ), )

ф                       > 0

^ M ( z , Au , t ), M ( z , z , kt ) _v

ф ( M ( Au , z , kt ), 1, M ( Au , z , t ),1 ) >  0

As ф is non-decreasing in the first argument, we have

ф ( M ( Au , z , t ),1, M ( A_tu , z , t ),1) >  0

and using (A), we get M ( Au , z , t ) >  1 .

Hence M ( Au , z , t ) = 1 . Therefore, A i u = z = Su which shows that u is a coincidence point of the pair (A, S).

Since, A ( X ) C T ( X ) , there exists V G X such that Tv = z = A i u = Su . Now, we show that A 0 v = z.

If A 0 v ≠ z, then by using inequality (3.2), take x = y n , y = v , we have

ф

^ M ( Ai y n , A о v , kt ), M ( Sy n , Tv , t ), _v M ( Sy n , A,y n , t ), M (Tv , A o v , kt ) _v

> 0;

n ^ да

< M ( z , A o v , kt ), M ( z , z , t ), M ( z , z , t ), )

> 0;

ф

_v M ( z , Av , kt )

Using (B), we get M ( z , AV , kt ) >  1 .

Hence M(z, AV, kt) = 1 . Therefore, A0V = z = Tv which shows that v is a coincidence point of the pair (A0,  T). Since, Ai and S are pointwise R-weakly commuting, there exist R > 0 such that

M ( ASu , SAu , t ) >  M ( Au , Su , t/R ) = 1.

This gives, A i Su = SA i u = AA i u = SSu.

Similarly, as A 0 and T are pointwise R -weakly commuting, we have A 0 Tv = TA 0 v and A 0 Tv = TA 0 v = A 0 A 0 v = TTv.

Take x = A i u , y = v in (3.2), we have

ф

( M ( AAu , Av , kt ), M ( SAu , Tv , t ), ) _v M ( SAu , AAu , t ), M (Tv , Av , kt ) ,

> 0;

ф ( M ( AAu , Au , kt ), M ( SSu , Au , t ),1,1 ) >  0;

As ф is non-decreasing in the first argument, we have

ф ( M ( AAu , Au , t ), M ( SSu , Au , t ),1,1) >  0;

Using (C), we get M ( AAu , Au , t ) >  1 .

This gives, M ( AAu , Au , t ) = 1 .

Therefore, A i A i u = A i u . Hence, A i z = z = Sz.

Similarly, by putting, y = A 0 v, x = u in (3.2), we get

Using (C) and (F), we have M ( z , w , t ) >  1 .

Hence, M ( z , w , t ) = 1 .

Therefore, z = w

By choosing A i , A 0 , S and T suitably, one can derive corollaries involving two or more mappings. As a sample, we deduce the following natural result for a pair of self mappings by setting A i = A 0 and T = S in above theorem:

Corollary 3.1. Let { A i } and S be self mappings of a fuzzy metric space (X, M, *) satisfying the following:

• (3.4)    the pair ( A i , S ) satisfies the E.A . property;

• (3.5)    for any x, y in X , ф in M 4 and for all t >  0 ,

  Ф

  
  

  ( M ( Au , AAv , kt ), M ( Su , TAv , t ), )

  
  

  _v M ( Su , Au , t ), M (TAv , AAv , kt ) _v

  
  

  > 0;

  
  

  ф

  
  

  ф ( M ( A o v , A o a v , kt ), M ( A v , A ₀ A ₀ v , t ),1,1 ) > 0;

  
  

  ( M ( Ax , Ay , kt ), M ( Sx , Sy , t ), ) _v M ( Sx , A.x , t ), M ( Sy , A.y , t ) _v

  
  

  > 0;

  
  

As ф is non-decreasing in the first argument, we hav

ф ( M ( A 0 v , A 0 A 0 v , t ), M ( a о v , A о A о v , t ),1,1) >  0;

M ( A , v , A , a v , t ) >  1;

therefore, M ( Av , AAv , t ) = 1;

This gives, A 0 v = A 0 A 0 v .

A0z = z = Tz.

Hence, A i z = A 0 z = Sz = Tz, and z is common fixed point of A i , A 0 , S and T.

Uniqueness: Let z and w be two common fixed points of A i , A 0 , S and T . If z ≠ w, then by using inequality (3.2), we have

• (3.6)    S(X) is a closed subset of X .

Then, { A i } and S have a point of coincidence each. Moreover, if the pairs ( A i , S ) is weakly compatible, then { A i }and S have a unique common fixed point.

By taking A i = A 0 = A and T = S in theorem 3.1, we get

Corollary 3.2. Let A and S be self mappings of a fuzzy metric space (X, M, *) satisfying the following:

• (3.7)    the pair ( A, S ) satisfies the E.A. property;

• (3.8)    for any x, y in X , ф in M 4 and for all t >  0 ,

  ф

  
  

" M ( Ax , Ay , kt ), M ( Sx , Sy , t ),' ( M ( Sx , Ax , t ), M ( Sy , Ay , t ) J

> 0;

ф

( M ( Az , Aw , kt ), M ( Sz , Tw , t ), )

_v M ( Sz , Az , t ), M(Tw, Aw , kt ) _v

> 0,

ф

^л M ( z , w , kt ), M ( z , w , t ),^л _v M ( z , z , t ), M ( w , w , kt ) _?

> 0,

^(M ( z , w , kt ), M ( z , w , t ),1,1 ) >  0, ф ( M ( z , w , t ), M ( z , w , t ),1,1 ) > 0.

(3.8) S(X) is a closed subset of X .

Then, A and S have a point of coincidence each. Moreover, if the pairs ( A, S ) is weakly compatible, then A and S have a unique common fixed point.

The following example illustrates Theorem 3.1.

Example 3.2. Let (X, M, *) be a fuzzy metric space where X = [0, 2) and define ф : [ 0,1 ] ^ R as ф ( t_x , t ₂, t ₃, t ₄ ) = 14 t_x — 12 1 ₂ + 6 t ₃ — S t ₄ . Clearly, ф satisfies all conditions (A), (B) and (C). Therefore, ф G M ₄. Define A, B, S and T by

A i x =A 0 x = 1,

Г 1

S ( x ) = 1 2

x G Q x e Q,,

T ( x ) = 1 1

x g Q x e Q

and M ( x , y , t ) =---:------- for all x, y in X = [ 0,

t + |x — y|

2 ) and t >  0 .Then with sequences

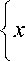
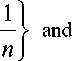
— 11

yn = — 1 in X, we have n lim Axxn = lim Sxn = lim A0 yn = lim Tyn = 1 in n ^^      n ^^     n ^^       n ^^

X which shows that pairs (Ai, S) and (A0, T) share the common (E.A.) property. By a routine calculation, one can verify the condition (3.2). Thus, all the conditions of Theorem 3.1 are satisfied and x = 1 is the unique common fixed point of Ai, A0, S and T.

Acknowledgment

The author wish to thank Dr. Sunny Chauhan, Dr Suneel Kumar and the referees for their very helpful suggestions and many kind comments .