A Comparative Study in Wavelets, Curvelets and Contourlets as Denoising Biomedical Images

Published Online February 2012 in MECS

Medical images are usually of low contrast and they are subject to complex type of noise in its acquisition and transmission. All medical images are corrupted by visual noise. The presence of noise gives an image a mottled, grainy, textured, or snowy appearance. This noise can be either image dependent or image independent. It comes from a variety of sources. No imaging modality is free of noise, but noise is much more prevalent in certain types of imaging procedures than in others. Nuclear images are generally the noisiest. Noise is also significant in MRI, Computer Tomography (CT), and ultrasound imaging (US). In comparison to these, radiography produces images with the least noise. Fluoroscopic images are slightly noisier than radiographic images, for reasons explained later. Conventional photography produces relatively noise-free images except where the grain of the film becomes visible.

Recently, a new member of the emerging representation family of multiscale geometric transform is the so-called contourlet transform which was developed in order to overcome limitations of traditional multi-resolution common representation such as curvelets and wavelets. Moreover, the contourlets transform has been efficiently used in medical image denoising [2], and obtained higher quality recovery of edges. In our work, we present a biomedical image” Axial-transverse” denoising using wavelet , curvelet and contourlet transform.

Extrema in gray scale images are often used to crudely extract the image structures. The image is considered as a topographic relief where gray levels correspond to altitude information. Therefore, the dark and light structures of the images correspond to the valleys and the domes of this relief. The regional maxima and minima are respectively the plateaus located at the top of the domes and the bottom of the valleys [9].

The curvelet, like the wavelet transform, is a multiscale transform, with frame elements indexed by location parameters and scale. The curvelet transform was designed to represent singularities and edges along curves much more efficiently than traditional transforms, i.e. using many coefficients for a given accuracy of reconstruction. So, in order to represent an edge to squared error 1/N requires 1/N wavelets and only about 1/ √ N curvelets [15].But contourlet transform is an efficient directional multiresolution expansion that is digital, thus contourlets transform is multiscale, local and directional contour segments and it is constructed via filter banks and can be viewed as an extension of wavelets with directionality than it Inherits the rich wavelet theory and algorithms, it starts with a discrete-domain construction that is amenable to efficient algorithms, and then investigates its convergence to a continuous-domain expansion.[15]. The expansion is defined on rectangular grids i.e. seamless transition between the continuous and discrete worlds.

This paper presents the image de-noising on different Axial-transverse MRI using wavelet transform, curvelet transform and contourlet transform. The performances of the three transforms are compared in terms of Peak Signal to Noise Ratio (PSNR) and the results are presented.

• II.  The Curvelet Transform

The Curvelet transform CT is a multiscale directional transform and a higher dimensional of the Wavelet transform which allows an optimal non adaptive representation of edges designed to represent images at different scales and different angles. [3][16] Curvelet has two mathematical properties [15][17]:

The curvelet frame [15] [о. J is the wave packet frame on L" R" based on the second dyadic decomposition:

fto = S_y C^ (x) et C_y = J ftov_Y to dx ; after the Frequency shells is ₂< _{< f < 2}K-1 ; and the Angular sectors is oc (o>, f) <  2~^k/1 therefore the approximation rate is optimal: Firstly we choose n largest coefficients C- in f = £, C,

T after llf-f_nll[2 :log(n)^a, yet no frame can do better for jumps along curves, finally the wavelet expansion is .

• •    Curved singularities should be approximated with some coefficients and in a non-adaptive representation so its name «curvelets."

• •    The Curvelet transform remain coherent waveforms under an action of a wave equation in the smooth medium

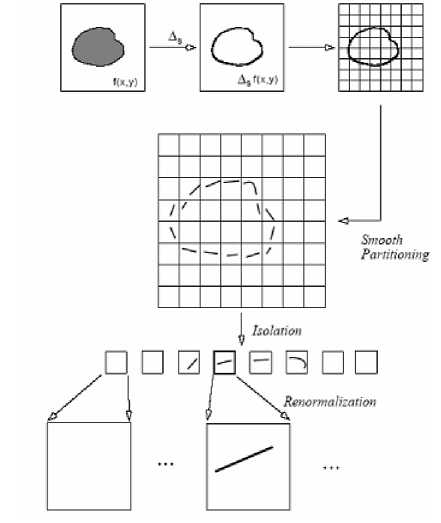
Figure 1. Curvelet Spatial decomposition

• III.    The contourlet Transform

Do and Vetterli [1] proposed an efficient directional multi resolution image representation called the contourlet transform. Contourlet transform has better performances in representing the image such as lines, edges, contours and curves than wavelet and curvelet transform because of its directionality and anisotropy.

The contourlet transform consists of two steps which is the sub band decomposition and the directional transform [4]. A Laplacian pyramid is first used to capture point discontinuities [14], then followed by directional filter banks to link point discontinuity into lineal structure. The overall result is an image expansion using basic elements like contour segments, [9] thus the term contourlet transform being coined [5] [10].

I Pttii^forni Dirrch'*ial Fillet Itj-iik

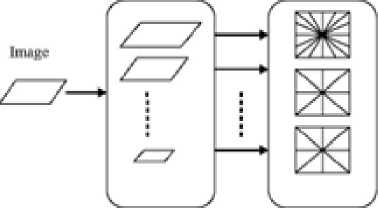
Figure 2. The Contourlet transform framework [8]

This figure shows a flow diagram of the contourlet transform

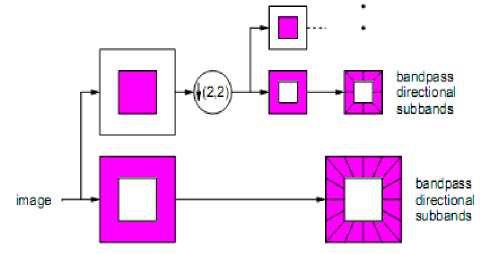
Figure 3. The Contourlet filter bank [6].

This figure shows the contourlet filter bank. Firstly, multi scale decomposition by the Laplacian pyramid [12] [13], then we applied a directional filter bank to each band pass channel. The method used is:

Figure 4. The directional filter bank

• IV.    The wavelet Transform

A wavelet is a localization function of the mean equal zero. Wavelet transforms always incorporate a result in a pyramidal representation. There are many cases where a set of successively smoother versions of an image are not down sampled. Wavelet transform is computationally efficient, and part of the reason for this is that the scaling or wavelet function used is often of compact support, i.e. defined on a finite and limited domain.

Wavelets also usually allow an exact reconstitution of original data. A sufficient condition for this in the continuous case wavelet transform is the wavelet coefficients and which allow reconstitution, are of zero mean. Wavelet functions are often wave like but clipped to a finite domain, that’s why they are so named. In the discrete case, the wavelet function is sampled at discrete mesh points using, [15] not Dirac sampling distributions, but rather a smoothing function, φ. Inner products with the wavelets can be performed in the original domain or in the Fourier domain; the former is preferred when the support of the wavelet function is small i.e., it is nonzero on a limited number of grid points. The discrete Wavelet Transform (DWT) can be derived from this theorem if the signal under consideration is band limited. If we consider images, we can‘t that the frequency band is always limited by the size of the Aperture’s camera. The DWT algorithm can be extended to other dimension by separable products of a scaling function φ and a wavelet ψ. For instance, the 2 dimensional algorithms are based on separate variables leading to prioritizing of vertical, horizontal and diagonal directions. The scaling function is defined by φ(t1, t2) = φ(t1)φ(t2), and the passage from one resolution to the next is achieved by:

Cj+1ki] = Е^.йЬп-гкШп-2l]C;[m,n] = [AA * CyJ^JkI] (1)

We used the DWT algorithm:

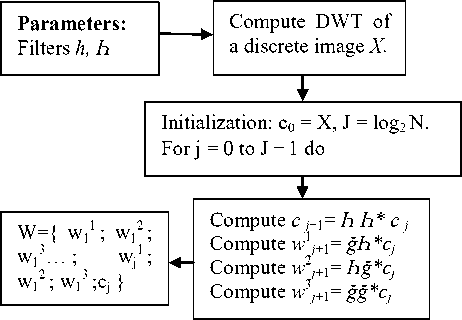
• V.  Materials and Methods

Neural Axial-transverse MRI of ten patients were denoised using wavelet curvelet and contourlet transforms. Various types of noise like the Random noise, Gaussian noise, Salt, Pepper and speckle noise were added to this image.

• >    A multiplicative noise factor of 0.05 is used in case of speckle noise.

• >    In case of Gaussian white noise, the mean is 0 and variance is 0.05.

• >    A Noise factor of 25 is used for random noise.

• >    The noise density used in case of salt and pepper noise is 0.04.

The PSNR is the most commonly used as a measure of quality of reconstruction in image denoising[10]. The PSNR for both noisy and denoised images were identified using the following formula:

Mean Square Error (MSE) which requires two m x n grey-scale images I and K where one of the images is considered as a noisy approximation of the other is defined as [11]:

The PSNR is defined as:

Here, MAXI is the maximum pixel value of the image. The PSNR of the images denoised is compared using wavelet, curvelet and contourlet transform for each type of noise mentioned above. Then the mean and standard deviation of each noise was calculated.

VI.  Results and Discussion

Figure 5. The original image

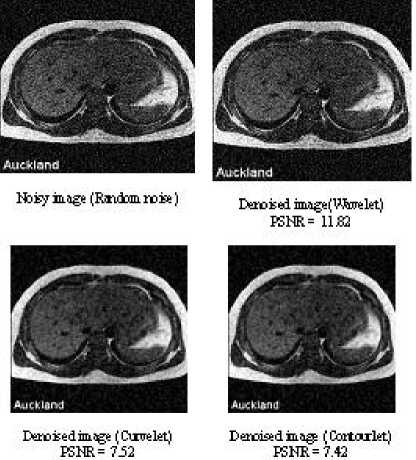
Figure 6. Denoising of an axial-transverse image of patient 1 with Random noise.

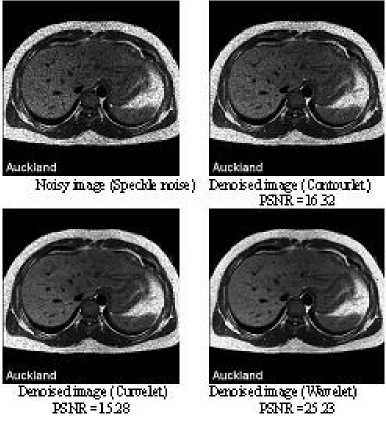
Figure 8. Denoising of an axial-transverse image of patient 1 with Speckle noise

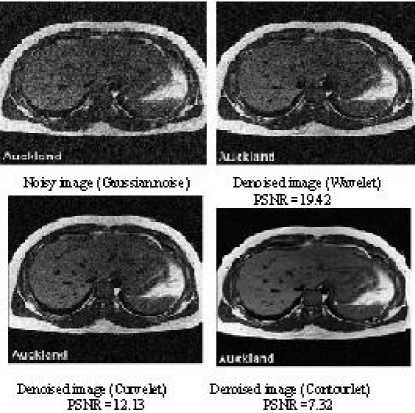
Figure 9. Denoising of an axial-transverse image of patient 1 with Gaussian noise

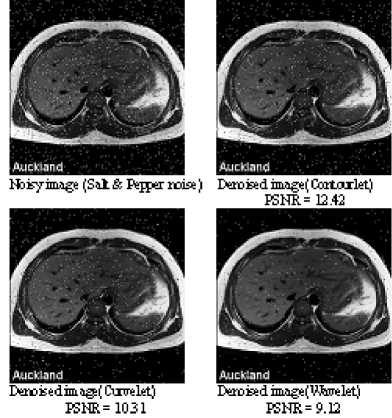
Figure 7. Denoising of an axial-transverse image of patient 1 with Salt and Pepper noise

TABLE I.     PSNR V alues for denoised A xial T ransverse image

Patient	Noise	Curvelet denoised  image PSNR (dB)	Wavelet denoised image PSNR (dB)	Contourlet denoised  image PSNR (dB)
1	Random noise	7.52	11.82	7.42
	Gaussian noise	12.13	19.42	7.32
	Salt & Pepper noise	10.31	9.12	12.42
	Speckle noise	15.28	25.23	16.32
2	Random noise	6.23	10.22	12.32
	Gaussian noise	12.11	9.25	13.32
	Salt & Pepper noise	13.36	13.26	15.02
	Speckle noise	18.26	17.5	20.34
3	Random noise	7.23	11.32	14.56
	Gaussian noise	13.23	10.65	20.32
	Salt & Pepper noise	14.25	15.22	22.6
	Speckle noise	15.98	19.32	19.26
4	Random noise	9.48	13.69	21.74
	Gaussian noise	9.32	12.36	19.65
	Salt & Pepper noise	10.69	14.23	18.33
	Speckle noise	15.98	18.23	22.38
5	Random noise	10.32	14.56	22.33
	Gaussian noise	8.65	13.65	21.97
	Salt & Pepper noise	8.14	15.23	19.33
	Speckle noise	16.32	18.27	21.12
6	Random noise	8.32	15.47	21.23
	Gaussian noise	6.25	11.23	16.23
	Salt & Pepper noise	12.96	15.32	11.25
	Speckle noise	13.02	14.39	19.83
7	Random noise	16.71	18.19	15.17
	Gaussian noise	9.72	11.13	21.96
	Salt & Pepper noise	12.65	18.17	20.39
	Speckle noise	12.10	15.37	18.93
8	Random noise	6.87	11.32	16.97
	Gaussian noise	11.97	19.23	21.87
	Salt & Pepper noise	18.13	16.32	15.98
	Speckle noise	12.45	17.37	21.65
9	Random noise	16.75	14.75	17.98
	Gaussian noise	19.32	14.27	18.19
	Salt & Pepper noise	19.32	11.23	16.34
	Speckle noise	19.32	12.65	22.65
10	Random noise	17.23	8.65	19.54
	Gaussian noise	19.54	11.23	19.23
	Salt & Pepper noise	16.87	6.32	21.32
	Speckle noise	14.56	12.34	18.98

We compared the result images after applying wavelet, Curvelet and Contourlet transform to MRI images. It can be observed that region in the result image of Contourlet transform is restored smoother than wavelet and Curvelet transform. The visual quality of various directional texture region of MRI image with Contourlet is also as clear as Curvelet. And the texture region of the MRI image is evident as in result image of wavelet transform. These observation results show that the Contourlet transform obtains better visual quality result image than wavelet transform and Curvelet transform.

Peak signal noise ratio (PSNR) is often employed to compare and measure the difference between result image and original image. It can be observed that the Contourlet transform obtains the highest PSNR value. So the Contourlet approach improves the PSNR value while obtaining high visual quality result images

• VII. Conclusion

In the all cases it was found that the Contourlet transform outperforms the Curvelet and Wavelet transform in terms of PSNR and the Contourlet denoised images appear visually more pleasant than the curvelet and the wavelet denoised images. The Contourlet transform provides high PSNR values and can remove the Gaussian white and Random noises from biomedical images very efficiently than the curvelet and the wavelet transform. The Contourlet transform doesn’t effectively remove the Speckle noise and Salt and Pepper noise from the biomedical images, and so Contourlet transform is not suited for removal of these two noises though it recovers the edges perfectly

Acknowledgment

We thank anonymous referees for their constructive comments.