A Comparative Study of Power Consumption Models for CPA Attack

Published Online March 2013 in MECS

Electronic cryptographic devices are widely used in embedded systems to secure secret information. Such devices store the secret key that is used in conjunction with the cryptographic algorithm. The algorithms are designed and analyzed to ensure a protection against mathematical attacks. But when the algorithm is implemented on hardware systems, the latter may cause side channel leakages used to reveal more information about the processed secret. Side channel attacks are an attacks based on information extracted from the physical implementation of a cryptosystem. For example, time execution [1], electromagnetic emanation [2] and power consumption [3].

Power analysis attacks exploit the correlation between the internal information and the power consumption of cryptographic devices. The Simple Power Analysis (SPA) attack [4] is based on detailed knowledge of the cryptographic algorithm and the visual inspection of the power consumption to guess the secret cryptographic keys. The Differential Power Analysis (DPA) attacks [3] is more powerful attack than SPA and requires less detailed knowledge of the implementation of cryptographic algorithm. It uses statistical analysis to extract information correlated to secret keys.

In 2004, the correlation power analysis (CPA) attack was proposed by Brier et al [5]. The CPA attack exploits the correlation between the real power consumption of cryptographic devices and the Hamming Distance model, in order to recover the correct key.

The Hamming Distance model was successfully applied on FPGA and ASIC implementation of cryptographic algorithms [5-12]. A new consumption model, so called Switching Distance, was proposed by Peeters et al in 2007 [13]. They applied the Switching Distance model in CPA attack against Sbox output on an 8-bit PIC-16F877. The same model was used with CPA attack against unprotected AES implementation on ASIC [14].

In this paper, in order to evaluate the security of the AES, we study the power analysis attack and specifically CPA attack. We also conduct a successful CPA attack against AES implementation on SASEBO-GII [15] board using Hamming Distance and Switching Distance models.

The organization of this paper is as follows. Section II describes the related background knowledge. The different power consumption models are presented in section III. Section IV presents the CPA attack methodology against AES. Section V presents the result of CPA attack and a comparison between the consumption models. Finally, we conclude in section VI.

• II.    Backgrounds

• A.    Advanced Encryption Standard

The Advanced Encryption Standard is a symmetric block cipher that process data blocks using cipher keys with lengths of 128, 192 and 256 bits [16]. Each data block consists of 4×4 array of bytes called the state. The AES is a round-based encryption algorithm. The number of rounds, Nr, is 10, 12, or 14, when the key length is 128, 192 or 256 bits, respectively. In the encryption of the AES algorithm, each round, except the final round, performs four transformations: AddRoundKey, SubBytes, ShiftRows and MixColumns, while the final round does not have the MixColumns transformation. The key used in each round, called the round key, is generated from the initial key by a separate key scheduling module.

Block diagram of the AES encryption is shown in Fig.

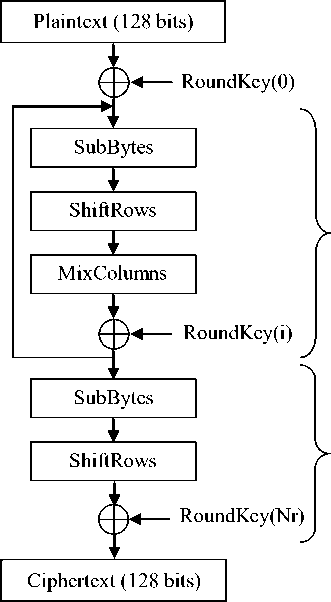
Figure 1. AES algorithm: Encryption structure

The SubBytes transformation is a non-linear byte substitution, operating on bytes independently. The SubBytes is invertible and is constructed by the composition of the following two transformations:

• •    Inversion in the  GF(2 8 )  field, modulo an

irreducible polynomial m(x) given by:

m(x) = x8 + x4 + x3 + x + 1                         (1)

• •    Affine transformation defined as follows:

Y = AX-1 + b, where A is a 8×8 fixed matrix and b is a 8×1 vector-matrix.

The ShiftRows transformation is a circular shifting operation on the rows of the state with different numbers of bytes. As seen in (2), the first row of the state is kept as it is, while the second, third and fourth rows cyclically shifted by one byte, two bytes and three bytes to the left, respectively.

s 0	s 4	s 8	s 12		" s 0	s 4	s 8	S 12
s 1	s 5	s 9	s 13	ShiftRows	S 5	s 9	s 13	s 1	(2)
s 2	s 6	s 10	s 14	'	S 10	s 14	s 2	s 6
s 3	s 7	s 11	S 15 _		_ S 15	s 3	s 7	S 11 _

The MixColumns transformation operates on the state column by column, treating each column as a four-term polynomial. The columns are considered as polynomials over GF(28) and multiplied x4 + 1 with a fixed polynomial a(x) given by:

a(x) = {03}x3+ {01}x2 + {01}x + {02}              (3)

In matrix form, the MixColumns transformation can be expressed as:

5	' 0, c		"02	03	01	01"	Г 5 0, C "
5	' 1, c	_ =	01	02	03	01	5 1, c	(4)
5	' 2, c		01	01	02	03	5 2, C
L 5	' 3, c .		L 03	01	01	02 J	L 5 3, c J

0 ≤ c ≤ 3

The AddRoundKey is a XOR operation that adds a round key to the state in each iteration, where the round keys are generated during the Key Expansion phase.

The AES algorithm takes the cipher key and performs a Key Expansion routine to generate a key schedule. The Key Expansion generates a total Nb(Nr + 1) words, where Nb = 4.

• B.    CPA attack

The hypothesis of the correlation power analysis (CPA) is that the measured power traces of the target device are correlated to the operands and operations being processed at that time. This type of power analysis technique requires a power model to attack a cryptographic device. The adversary needs to build a hypothetical model of the cryptographic device under attack. He can recover secret data by analyzing the power consumption usage during cryptographic operations. An efficient way to calculate the correlation coefficient,  p,  between theoretical predictions of the power consumption and real power measurements is to use the Pearson correlation function.

The Pearson correlation function is the most widely used way to compute the linear relationship between data. Whence, it is an excellent choice for statistical analysis tool when it comes to perform CPA attacks.

Given N plaintexts/ciphertexts, P the predicted power calculated by a power model and W the equivalent real power traces measured when processing the cryptographic operation. The correlation coefficient p is defined as:

.     .       Cov ( W , P )

^P^  ^аг (W ) ^аг ( P )

where W and P are N-dimension vectors, Cov denotes the covariance operation, and Var denotes the variance operation.

The Pearson correlation coefficient can take values from -1 to +1. A value of +1 shows that the W and P are perfectly linear related by an increasing relationship, a value of -1 shows that W and P are perfectly linear related by a decreasing relationship, and a value of 0 shows that W and P are not linear related by each other.

The process of conducting a CPA attack as presented in [14].

• •    Select an intermediate point of the processing algorithm. This point must depend on the known variable and the secret keys.

• •    Measure the real power consumption of the cryptographic device, using digital oscilloscope, during the execution of the processing algorithm.

• •    Predict the power consumption with certain leakage model as the Hamming Weight, Hamming Distance or Switching Distance.

• •    Compute the correlation between the assumption power and the measured power trace. The value of the highest correlation coefficient corresponds to the correct key guess.

• C.    Power consumption in CMOS devices

The CMOS technology is certainly the most widely used in current digital design applications. The total power consumption of CMOS gate is the sum of static and dynamic power, as shown in (6).

P ,= P - + P, ¹ total ¹ static + ¹ dynamic

The static power consumption P static is due to the leakage currents in transistors. The dynamic power consumption P dynamic is the sum of the short-circuit and the switching power consumption, as shown in (7).

¹ dynamic   Swivitcnin g + ¹ short - circuit

The short-circuit power consumption is produced when NMOS and PMOS transistors are conducting simultaneously during the switching of CMOS gates. The switching power consumption is due to the charge and discharge of the load capacitance. The short-circuit current of a logic gate is negligible compared to the switching current. The expression of the dynamic power consumption of a CMOS gates is expressed as follows [7]:

P dynamic = CV D P ■ f (8)

where C L is the gate load capacitance, V DD the supply voltage, P_{0 я} the probability of a 0 ^ 1 output transition and f the clock frequency.

Equation (8) shows that the total power consumption of a CMOS device can be estimated proportionally in accordance with the output transition number from 0 to 1, in other words the power consumption of CMOS circuits is data-dependent.

• D.    SASEBO-GII

The SASEBO-GII board was developed by the National Institute of Advanced Industrial Science and Technology (AIST) [15]. The SASEBO-GII is a newly developed FPGA board suitable for additional extended experiments such as one for security evaluation for a comprehensive cryptographic system combining various elemental technologies or one for a large circuit implemented with a variety of countermeasures.

The SASEBO-GII board includes two FPGAs: a Cryptographic FPGA (XC5VLX30 or XC5VLX50-1FFG324, Virtex-5 series) and a Control FPGA

(XC3S400A-4FTG256- Spartan-3A series). Researchers can use the SASEBO FPGA platform to evaluate the robustness of cryptographic algorithms against side channel attacks [17-21].

• III.    Power Consumption Models

In the CPA attacks, an attacker uses a power model of the device under attack to predict its power consumption. These predictions are then compared to the real measured power consumption in order to recover secret key. The quality of the model has an important impact on the efficiency of the attack and it is therefore of primary importance. The power models currently used in these instances are the Hamming Weight (HW), the Hamming Distance (HD) and the Switching Distance (SD) models.

• A.    Hamming Weight

The Hamming weight model (HW) is the most basic power consumption model. It is most applicable to estimating the power consumption of a circuit when the attacker does not know the consecutive values of the data in some part of the process. This model considers that a 0 does not lead to an excess of power consumption, whereas a 1 involves a significant amount of power consumption. Therefore, in this model, it is assumed that the power consumption is proportional to the number of bits that are set in the processed data.

• B.    Hamming Distance

The Hamming Distance model (HD) was proposed by Brier et al in [5], it is based on the relation between the power consumption and switching activity in CMOS device. The Hamming Distance model is proportional to the number of 0 ^ 1 and 1 ^ 0 transitions. It is assumed that the power consumption for 0 ^ 1 and 1 ^ 0 transitions have the same amount of power consumption.

Let M 1 and M 2 are two consecutive intermediate values of a running algorithm during a target implementation. The power consumption W is modeled as follows:

W = HD ( M _1; M ₂ ) = aHW ( M ₁ © M ₂ ) + b (9) where a denotes the scalar gain between the Hamming Distance and the power consumption W, b denotes the offsets, time dependent and noise.

• C.    Switching Distance

The Switching Distance model (SD) is based on the fact that 0 ^ 1 and 1 ^ 0 transitions consume different power in CMOS device. The Switching Distance of the transition 0 ^ 1 is assigned 1, the Switching Distance of the transition 1 ^ 0 is assigned Ф which is named Switching Distance factor (see table 1) [14].

Table 1. Power Consumption Models of CMOS Transition

Transitions	HW	HD	SD
0 > 0	0	0	0
0 ^ 1	1	1	1
1 > 0	0	1	Ф
1 > 1	1	0	0

^ ⁽ P measur'ed , P predicted )

The correlation coefficient between the measured power consumption, denoted P measured , and the predicted power consumption P predicted is calculated as follows:

Cov ⁽ P measured , P predicted )

VarK ⁽ P measured ) Var^ * ⁽ P predicted )

• IV.    CPA Attack Methodology

In this section, we will describe the process of the CPA, based on the Switching Distance model against AES on SASEBO-GII.

In this work, we use the traces given by the "DPA contest v2" competition. The acquisitions have been performed on a SASEBO-GII board. The DPA Contest v2 was organized by the VLSI research group from the COMELEC department of the Telecom ParisTech french University.

The AES transforms 128-bit plaintext with the 128-bit key to 128-bit ciphertext. Each round has a round key: k 1 to k 10 , computed from the original key k 0 . We attack the last round encryption because the latter has been isolated from the other rounds and has relatively clear power signals [14]. Since the AES Key Expansion is invertible, it is then possible to compute the initial secret key, k 0 , going backwards.

Then we predict the power consumption of the last round encryption. Let C 10 the output ciphertext of the last round and D 10 the input data to this round. The ciphertext C 10 is picked up to compute D 10 by Inverse-ShiftRows and Inverse-SubBytes using the guessed keys K 10 (256 possible values).

D 10 = SubBytes ^{- 1} ( ShiftRows ^{- 1} ( K ₁₀ ( _guess ) Ф C ю ) ) (10)

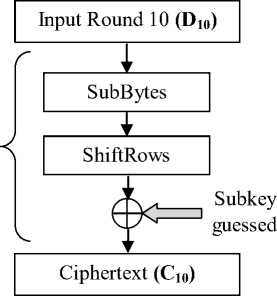
Figure 2. The final round of AES encryption

After that, the prediction of power consumption of the last round is calculated by the Switching Distance (SD) between C 10 and D 10 as presented in (11).

P predicted = SD ( D 10 ,C io ) (11)

where Cov(P measured ,P predicted ) is the covariance between the measured power consumption and the predicted power consumption, the Var(P measured ) and Var(P predicted ) are the variance of the P measured and the P predicted respectively.

The correlation coefficient measure the linear relationship between P measured and P predicted . Its value will always be between -1 to 1, when the correct key guess appears, the correlation coefficient is supposed to be highest.

• V.    Results and Discussion

In this section, we present the results of CPA attack AES-128 implemented on SASEBO-GII. The model to predict the power consumption is the Switching Distance. The Switching Distance factor ( Ф ) is 1,5. Liu et al show in [14] that for Ф equal to 1.5, the 16 byte keys of AES can be recovered with least power traces.

If the CPA attack is successful, we expect that only one value, corresponding to the correct key guess, leads to a high correlation coefficient. The experimental results for the correlation power traces are shown in Fig. 3. The peak corresponding to the correct subkey guess is clearly visible.

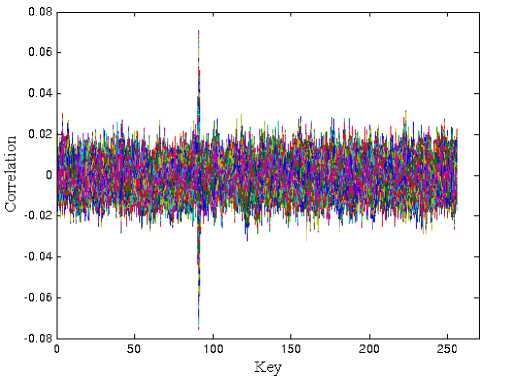
Figure 3. The 256 correlation for a correct Subkey guesses of CPA attack

The original key bytes is 00 00 00 00 00 00 00 03 24 3f 6a 88 85 a3 08 d3 in hexadecimal numbers. The corresponding final round key is 53 9f b1 88 40 7e 2b 3f 2d 5a 24 5f 50 fe be e1.

Table 2. Number of Power Traces to Recover all the Key Bytes

Key Bytes	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
SD=1.5	5.7	4.8	3.6	6.1	11.1	7.6	8.4	8.5	3	4.2	6.8	4.4	4.9	9.2	3.9	9.2
HD	5.6	5.3	5.6	6.2	12.7	8	8.5	11	3	4.3	6.9	5	6.5	9.7	4.3	9.3

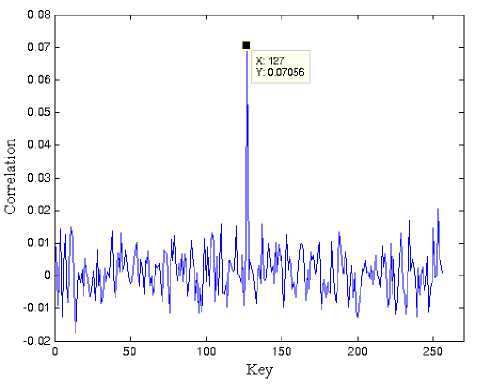
Figure 4. Successful CPA attack on the last AES round based on

SD model

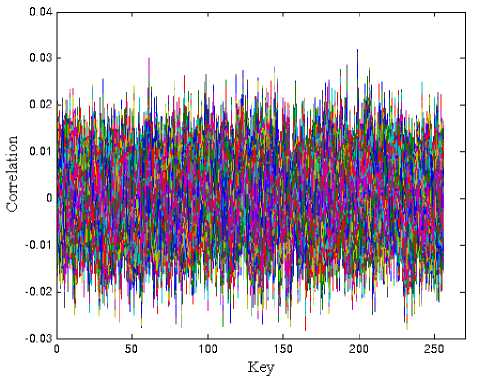
Figure 6. Failure CPA attack on the last AES round based on

HW model

Fig. 4 shows clearly that the peak corresponding to the sixth byte of the correct key becomes higher while the peaks corresponding to the incorrect key guesses remain constant. As it is seen, the plot shows that the Switching Distance model makes correct predictions for the real power consumption.

The results of CPA attack, based on Hamming Distance and Hamming Weight models, are shown in Fig. 5 and Fig. 6 respectively. These figures represent the assumption of all 256 subkey guesses.

Fig. 5 illustrates the success of CPA attack to recover the ninth byte of key using the HD model. However Fig. 6 shows that the CPA attack, based on HW model, fails to recover the correct key, that means that the HW model cannot make correct assumption about the real consumption of SASEBO-GII board.

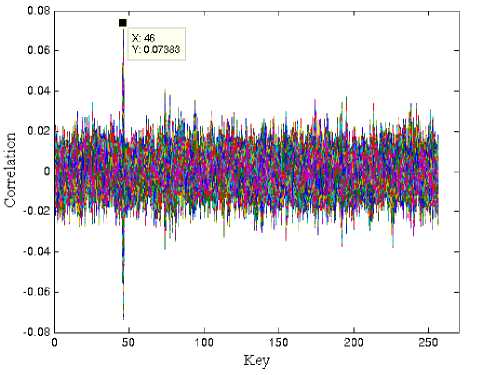
Figure 5. Successful CPA attack on the last AES round based on HD model

We have already demonstrated that our attack works well together with the SD and HD models. The only remaining question is how many power traces are needed to determine each byte of the correct key. In order to determine the minimum of number traces, we calculate the correlation coefficient between the predicted power consumption and measured power consumption for various numbers of traces. As revealed in Fig. 7, after approximately 4000 measurements, the tenth key can be distinguished. The number of power traces used to recover all the 16 byte keys of AES is shown in table 2. Note that, all numbers are in unit 1000. As an example, the first byte of the AES key can be recovered at 5700 traces.

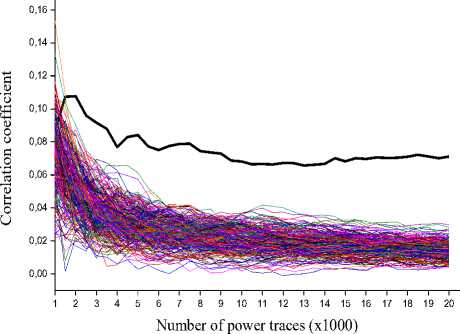
Figure 7. The correlation coefficient of recovering the tenth byte of the correct key

In order to compare the efficiency of the Switching Distance model with the Hamming Distance model, we reconduct the CPA attack using the same power traces with the Hamming Distance model. We list the new result at the final line of table 2.

Table 2 shows that the number of power traces to determine each byte of the correct key is decreased when using the Switching Distance model. As well, for these two models, the number of power traces is variable from a byte to another, this means that the power assumption with each consumption model does not reflect the real consumption at the same degree.

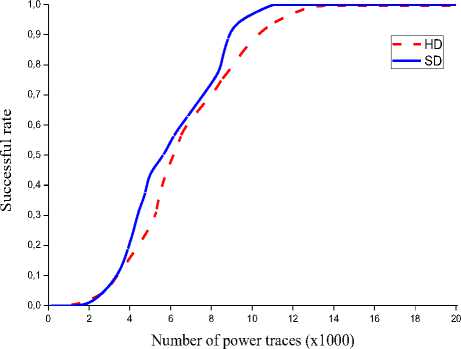
Figure 8. The successful rate of CPA attack against AES on SASEBO-GII

Fig. 8 illustrates the successful rates of Switching Distance and Hamming Distance models. Successful rates express the number of power traces when all the key bytes can be recovered [17]. With Hamming Distance model, 100% appears at about 12700 power traces. While using Switching Distance model, 100% appears at about 11100 power traces, which means the power traces of recovering keys have been decreased by 12.6%.

• VI.    Conclusion

In this paper, we conduct a CPA attack against AES on SASEBO-GII board with Switching Distance and Hamming Distance models. We compare between the two power consumption models in terms of number of power traces needed to recover the correct key.

Compared with Hamming Distance model, Switching Distance model can decrease the number of power traces needed to recover the correct keys by as much as 12.6%.