A Compressed Representation of Mid-Crack Code with Huffman Code

Most computer vision applications that are designed for automated inspection or recognition of objects require extraction of the contour of the boundary of objects in the recognition phase. Many applications also require to measure different geometric features of objects like perimeter and area. Different encoding algorithms are available for contour tracing of binary objects and their encoding efficiency is very important in representing, recognizing, storing, analysing, and transmitting the shape of the objects.

Chain codes are widely used contour tracing algorithm in image processing and pattern recognition applications. In 1961, Freeman introduced the method for representing the boundaries of digital curves using chain code [1]. An adaptive algorithm for converting the quad tree representation of binary image to its chain code representation was presented in [2] and a way of computing local symmetry of the contour of an object from its chain code representation was shown in [3]. The chain code moves from the centre of a pixel to the centre of the adjacent pixel along the boundary of the objects following the eight-connected rule. As the classical chain codes are fixed-length code, in the eight-direction

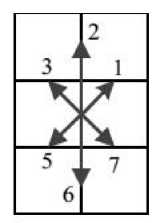
(c) Mid-crack code on the vertical crack

Fig.1. Contour Coding Schemes: Chain Code, Crack Code, and MidCrack Code [4]

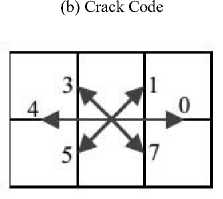
(d) Mid-crack code on the horizontal crack

A second contour encoding scheme, crack code, can accurately estimate the area of an object. It is also a fixed-length encoding scheme and defines four directions using a 2-bit numbering scheme as {i| i = 0,1,2,3} to denote a counter-clockwise angle of 90° x i with respect to the positive x-axis (see Fig.1(b)). In this scheme, the contour is formed by traversing the outer edge of the pixels along the boundary of the objects. Dunkelberger and Mitchell [5]; and Wilson and Batchelor [6] had provided a detailed description of the crack coding scheme. Although, this scheme accurately calculates the area of an object, major drawbacks of this scheme are that it generates much more code with compared to the chain

code and overestimates the perimeter of the object.

Fig.2. Silhouette with the Inside and Outside Chain Coded Contours (Dashed Lines) and the Crack Coded Contour (Solid Line) [7]

A third scheme, the mid-crack code [5], was introduced to overcome the limitation of the chain code and the crack code in computing area and perimeter of objects. It is a variation and an improvement of classical contour tracing approaches between crack code and chain code. In contrast to the chain and the crack code, it moves along the midpoint of the outer edge of the pixels along the boundary of the objects. Mid-crack code also defines eight directions (counter-clockwise) with respect to the positive x-axis using a 3-bit numbering scheme. However, it requires more moves in mid-crack code than the chain code to represent the same object. Although, all the contour tracing methods reduce the size of the objects (in terms of the amount of information requires to represent the object) but none of them are developed to produce efficient coding to minimise the number of bits require to encode the shape of an object. Though the angle differences between two adjacent pixels are not equally probable, i.e., frequencies of moves in different directions are not the same, all the above mentioned methods do not take the frequencies of moves in different directions into account while assigning codes. Rather, they use fixed-length codes (2 or 3 bits) to denote different directions irrespective of their occurrence frequencies. But encoding moves in different directions with predefined fixed-length codes does not attain an optimum performance as every move consumes an equal number of bits. A variable-length encoding scheme can help to increase the compression performance.

Huffman code [8] is a variable-length encoding scheme that takes the frequency of occurrence of characters into account and assigns variable length codes to characters, and thus represents a message with fewer number of bits. By utilising the compression performance of the Huffman code, the chain code has been modified by Liu and Zalik [9]. However, no attempts have been made to increase the compression efficiency of the mid-crack code. In this paper, a new representation of the mid-crack code is proposed based on the Huffman code without altering the basic structure of the mid-crack code. Experimental results suggest that the new representation contributes towards improved compression performance of the midcrack code.

The rest of the paper is organized as follows: Section II presents the background study of the mid-crack code, the Huffman code and the related works. The new compressed representation of the mid-crack code using the classical Huffman code is shown in Section III. Experimental results and discussion are presented in Section IV. Finally, concluding remarks are presented in Section V.

• II. Background Study And Related Works

• A.    Mid-Crack Code

Mid-crack code defines eight directions using a 3-bit numbering scheme as shown in Fig.1 (c) and Fig.1 (d). In mid-crack code, moves are defined from the midpoint of one crack to the midpoint of an adjacent crack [4]. The length of horizontal and vertical (even valued) moves is 1, and diagonal moves (odd valued) have length . Unlike the chain and the crack code there are two restrictions on the moves in the mid-crack code. Moves in directions denoted by 2 and 6 are not allowed from the horizontal crack, and moves in direction denoted by 0 and 4 are not allowed from the vertical crack (see Fig.1 (d) and 1 (c)). A mid-crack coding scheme is described by Shih and Wong in [10]. A thinning algorithm for binary objects based on the mid-crack code is shown in [11].

(a) Chain Code

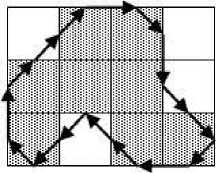
(b) Mid-crack code

Fig.3. Comparison Between Chain Code and Mid-Crack Code [4]

It is mentioned earlier that the mid-crack code has higher accuracy over the chain and the crack code in estimating perimeter and area of objects. The superiority of mid-crack code in computing perimeter and area was experimentally verified in [5]. A common property of the chain code and the mid-crack is that both the techniques use a fixed-length encoding scheme. However, one disadvantage of mid-crack code, as seen in Fig.3 (b), is that it takes more moves with compared to the chain code to encode the boundary of an object. As all the contour coding techniques uses fixed-length encoding schemes, they do not attain an optimum performance because every move consumes an equal number of bits irrespective of their occurrence frequencies. A variable-length encoding scheme that can take the frequency of occurrence of distinct move into account to assign code can be employed to increase the compression efficiency of the contour encoding schemes. A significant number of researchers like [9], [12]–[15] have performed a considerable amount of research to improve the compression performance of the chain code. However, to the knowledge of the author, so far no attempt has been made to encode the mid-crack code with a variable-length coding scheme to have a better compression performance.

• B.    Huffman Code

In computer science and information theory, Huffman code is an entropy encoding algorithm used for lossless data compression. It takes into account the probabilities at which different symbols are likely to occur and results in fewer data bits on the average. For any given set of symbols and associated occurrence probabilities, there is an optimal encoding rule that minimizes the number of bits needed to represent the source. Encoding symbols in predefined fixed-length code does not attain an optimum performance, because every character consumes an equal number of bits irrespective of their degree of contribution to the whole message. Huffman code tackles this by generating variable length codes, given a probability usage frequency for a set of symbols. It generates prefixcode, i.e., none of the code is a prefix of any other code, to facilitate unambiguous retrieval of information.

Applications of Huffman code are pervasive throughout computer science. The algorithm to completely perform Huffman encoding and decoding is explained in [16]. It can be used effectively where there is a need for a compact code to represent a long series of a relatively small number of distinct bytes. For example, Table 1 shows 8 different ASCII characters, their frequencies, ASCII codes and the codewords generated for those symbols using the Huffman code. It is seen from the table that the codeword to represent each character is compressed and the most frequent character gets the shortest code. In this example, the compression ratio obtained by Huffman code is 64.16%.

Table 1. Example of application of Huffman code to Compress ASCII Characters

Symbols	Frequency	ASCII Code	Codewords using Huffman code
A	50	01000001	00
B	35	01000010	101
C	42	01000011	110
D	22	01000100	1001
E	65	01000101	01
F	25	01000110	1111
G	9	01000111	1000
H	23	01001000	1110

It is believed that the mid-crack code can also be compressed using the Huffman code. But an interesting thing to notice that the codewords in the mid-crack code are already well-compressed with compared to the ASCII codes because there are only 8 different moves possible in mid-crack code hence the moves are represented with 3-bit codes (not a byte). Therefore, application of Huffman code to represent the mid-crack code can help to compress it further in most of the cases, however, a much lower compression ratio is expected in this case because of the limited compression scope. Another important thing to keep in mind that if the characters that are required to be encoded using Huffman code are equally occurring in the input message then further compression of those characters are not possible.

• C.    Related Works

Different approaches like chain code, crack code and mid-crack code are used to encode the contour of digital images. All the approaches are developed with an aim to reduce the amount of information to represent an object. However, all of them use fixed-length encoding schemes to represent the angle difference between two adjacent pixels along the border of an image, hence, they do not obtain a maximum compression performance. The applicability of the variable-length encoding schemes to improve the compression efficiency of the contour encoding schemes has not gone unnoticed. Specially, for the chain code, several efforts have been made to apply variable length encoding schemes to encode the angle difference between the border pixels of images. In [9], a new variation of the Freeman chain coding scheme has been proposed based on the Huffman code. Authors in [9] showed that the probability of relative angle difference between two border pixels of an image in different directions are not the same, hence, they decided to use variable-length code instead of fixed-length code to encode the moves in different directions. The authors used the classical Huffman code to generate variablelength codewords based on the occurrence frequencies of moves in different directions.

In [15], two different variable-length versions of the vertex chain code [17] have been proposed. In the original version of the vertex chain code, only three elements (1, 2, and 3) are used to encode an image, hence two bits fixed length codes (01, 10, and 11) are used to denote the three elements. The authors in [15] showed that the occurrence probability of element 2 is greater than the other two, therefore they used binary digit 0 to denote code 2, 10 for code 1 and 11 for code 3. This extension of the vertex chain code is named as the variable-length vertex chain code. In the second extension of the vertex chain code, the authors introduce five codes instead of three codes of the original vertex chain code to encode the contour of an object. Afterwards, they have shown experimentally that the five different codes are not equiprobable, thus variable-length codes are used to denote five different codes. Similar to the approach presented in [9], this approach also used the Huffman code to generate the variable-length codes.

Recently, in [14], a new variable-length version of the chain code has been proposed. The approach is proposed by treating binary bits unequally. The authors considered the costs of binary bits as unequal similar to that of the Morse code where a dash ( - ) is three times longer than a dot ( · ) in duration. Based on the occurrence frequency of the moves in different directions, the approach generates the variable-length codewords to denote the moves using Huffman code with unequal letter cost algorithm [18].

• III.    Compressed Represntation of Mid-crack Code with Huffman Code

The mid-crack code assigns 3-bit codes to denote moves in different directions, i.e., ignores the probability of occurrence of a certain move in the sequences of moves. As the moves in different directions are not equiprobable, it is worth trying to have a compressed representation of these codes. The new representation of the mid-crack code is proposed by taking the frequency of moves in different directions into account to assign the codewords to denote different directions. The idea is to assign a variable length code to denote 8 different directions and the assignment is performed in a way that the shortest code is assigned to the most frequent moves and vice versa.

The uniquely decodable variable-length codes to denote different moves in the mid-crack code is obtained by using the Huffman code technique. The process is shown in Fig.4. In the first step, the input image is provided to the mid-crack code generator block. The mid- crack code generator obtains the mid-crack code representation of the contour of the image using existing mid-crack code generation algorithm. In addition to the coordinate of the starting pixel of the mid-crack code and the code itself, i.e., sequences of moves, this block also counts the number of moves in different distinct directions. The number of moves in different directions along with the moves themselves is then fed to the Huffman code generator. It treats each move as a distinct symbol and the number of occurrences of each move in the mid-crack code as their frequency. Based on these data and using the Huffman code algorithm, the variable length codeword is generated for each move. In the next step, the codewords are assigned to their respective moves to have a new representation of the moves in the mid-crack code. In the new representation, moves are denoted using variable length codewords, but as mentioned earlier the sequences of moves in the midcrack codes are not altered. In this way a compressed representation of the mid-crack code is obtained.

Fig.4. Process of Producing Compressed Mid-Crack Code

The process is illustrated by applying it to an example image, shown in Fig.5. Table 2 shows the frequencies of angle difference between two adjacent moves in the midcrack code representing the contour of the example image and the codewords assigned by the classical mid-crack code and the new representation. For this particular image, the most frequent move is in 180° and the least frequent is in 270° angle. Therefore, the new representation assigns the shortest code (01) to represent a move in 180° and the longest code (11110) to represent a move in 270°. To encode the contour of the plane image, the mid-crack code takes 4332 bits, on the other hand, the new compressed representation of the mid-crack code takes 4098 bits. As a result, the compression ratio obtained by the new representation is 5.402%.

Fig.5. An Example Image

IV. Results and Discussion

A variable-length scheme is considerably better than a fixed-length scheme, as the variable-length scheme assigns shorter codewords to frequent symbols and longer codewords to infrequent ones. To evaluate the performance of the new compressed representation of the mid-crack code, experiments were performed on 100 images of arbitrary shapes. Fig.6 shows sixteen of the test images. For each of those images, mid-crack code was generated and variable-length codewords were generated by compressed mid-crack code focusing on bit reduction. Bits required by the classical mid-crack code and the

Table 2. Frequency of Moves in Different Angles and the Code words Assigned by the Mid-Crack code And the Compressed Mid-Crack code

Angle Change Frequency Mid-crack Code Compressed Mid-crack code 0° 298 000 00 45° 205 001 110 90° 84 010 11111 135° 107 011 1110 180° 329 100 01 225° 199 101 101 270° 59 110 11110 315° 163 111 100 Total Bits= 4332 Total Bits= 4098 compressed mid-crack code to encode the contour of the images of Fig.6 along with the compression performance for each of those images are shown in Fig.7. As midcrack code assigns fixed-length code to define moves in different directions, the number of bits required by this method is proportional to the total number of moves required to encode the contour of an object. So, from Fig.7, it is seen that the maximum number of moves is required to encode the horse image (Fig.6 (n)) and the minimum number of moves is required for the shark image (Fig.6 (k)).

The experimental results for all 100 images are shown in Fig.8 and Table 3. Fig.8 shows the comparison between the mid-crack code and the new representation of the mid-crack code in terms of bits required to represent the contour of objects. As seen in the figure, for most of the images, the new representation takes the fewest number of bits to represent the contour of the objects. Out of the 100 images only for 6 images, both the representations of the mid-crack code takes an equal number of bits, i.e., no compression is obtained. For other images the experiments suggest that the new representation reduces the numbers of bits by 1.29% in the worst case scenario; in the best case it reduces the number of bits by 23.12%; and on average it reduces the number of bits by 4.48%.

As the images were of different dimensions and shapes, a varied number of total moves in different directions were required to represent the shape of the images. A varying trend is seen in the percentage of moves in each of the eight directions with the varying number of total moves

(see Table 3). As seen from Table 3, the best average compression performance is obtained for those images for which the total number of moves in the mid-crack codes are in between 1301 to 1700, whereas the least average compression performance is obtained for the images having the total number of moves in the range between 1701 and 2100. It is also seen from Fig.7 that the maximum compression performance is obtained for the fighter jet image (Fig.6 (g)) although it does not have the maximum number of moves and the least compression is obtained for the crab image (Fig.6 (p)) although it has a second maximum number of moves. Therefore, by observing the trends of compression performance from Fig.7 and Table 3, it can be said that the compression performance is not dependent on the total number of moves, rather it depends on the shapes of the images, i.e., the relative angle difference between the border pixels of the images. If the mid-crack code of the contour of an image is dominated by the moves in some certain directions, then due to the nature of the Huffman code a better compression performance is obtained. Because, in such situations, moves in some special directions are most frequent therefore they are given the shortest length code, and thus they contribute a relatively less number of bits with compared to the least frequent moves. If the midcrack code of an image contains equal number of moves in all eight directions or the entropy of the frequencies of the moves in the different directions are very much closer to 3, then no further compression of the mid-crack code is possible. For this reason, no compression was obtained for 6 images.

Table 3. Trends of Moves in Different Directions and Compression Performance of the New Representation for Images with Different Ranges of Moves

Ranges of moves	Average Percentage of moves in different angles								Average Compressio n Ratio (%)
	0°	45°	90°	135°	180°	225°	270°	315°
101-500	10.79	9.58	15.01	13.94	10.71	11.10	13.56	15.31	3.37
501-900	10.61	13.26	13.81	12.94	10.54	12.15	14.99	11.70	3.68
901-1300	12.69	11.76	12.03	13.07	13.70	10.65	12.13	13.97	4.44
1301-1700	12.72	12.99	12.49	11.14	13.67	12.41	12.12	12.46	5.16
1701-2100	8.62	11.67	14.53	15.45	8.55	11.27	15.00	14.91	3.03
2100-above	8.89	15.43	13.67	13.28	7.60	15.49	14.89	10.75	4.03

(a) Butterfly

(c) Man

(d) Ostrich

(b) Plane

(e) Cow

(f) Deer

(g) Fighter Jet

(n) Horse

(p) Crab

Fig.6. Sixteen Test Images

(i) Bird

(o) Rat

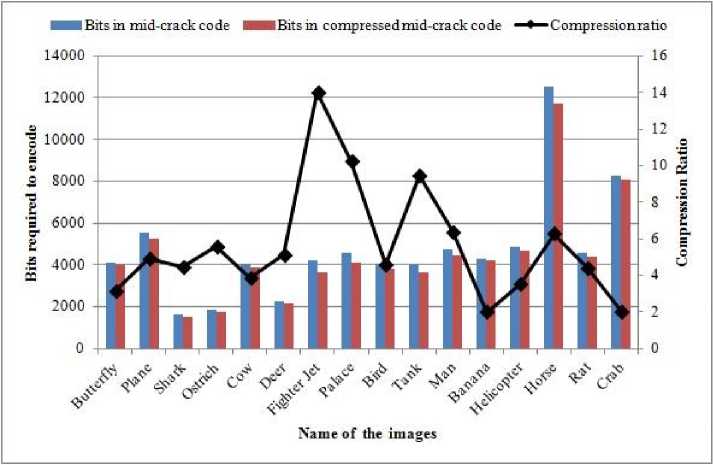
Fig.7. Comparison of Performance between Mid-Crack Code and Compressed Mid-Crack Code For Sixteen Test Images

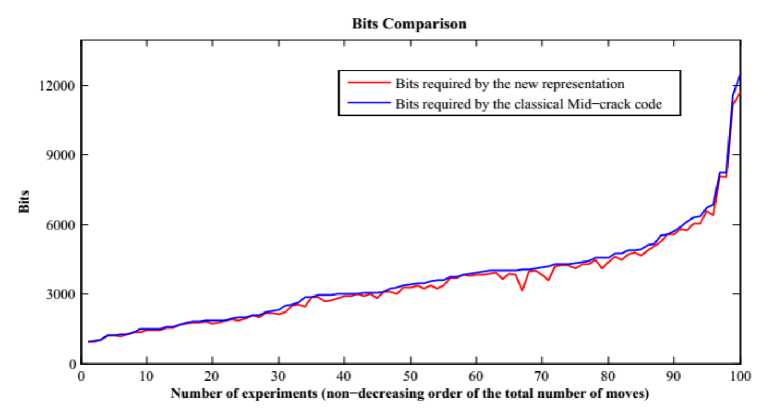
Fig.8. Comparison of Performance between Mid-Crack Code and Compressed Mid-Crack Code For 100 Test Images

• V. Conclusion

The encoding efficiency to represent the shapes of objects is very important in digital object recognition and analysis. Mid-crack code is an efficient lossless compression method for representing the contours of binary objects. It has higher accuracy over other contour encoding approaches in calculating perimeter and area from the contour representation of the objects. By encoding moves in different angles using predefined fixed-length codewords, the mid-crack code does not attain an optimum performance in terms of compression, because every symbol consumes an equal number of bits.

Statistical analysis shows that the moves in different directions in the mid-crack code are not equiprobable, therefore variable-length codes are selected as a potential solution to increase the compression performance of the mid-crack code. In this paper, Huffman code is used as the method to obtain the new representation of the midcrack code. The comparison of bits requirements between the classical and the new representation of the mid-crack code confirms that the new representation requires a fewer number of bits than the classical approach to represent the contour of the objects. At present, bit consumption is taken into account to compress the midcrack code. In future, transmission cost of bits can be considered to obtain a low power version of the midcrack code for high performance data transmission.