A fault-tolerant improved OLSR protocol using k-Connected m-Dominating set

Published Online December 2017 in MECS

Ad hoc networks are characterized by limited energy, short transmission range and absence of routers. Lack of access points in these networks puts the onus of routing on the participating nodes. Moreover, due to limited transmission range, a node cannot communicate with far-off nodes directly. Hence, multihop routing is used by a node to communicate with other nodes that are not within its transmission range. Also, lack of central administration makes self-organization of nodes essential for routing. Further, the mobility of nodes, node failures and link failures which are a common phenomenon in mobile ad hoc networks affect routing. These features which are inherent in ad hoc networks make routing a challenging task.

Flooding of messages can be used as a solution for routing. But this results in the broadcast storm problem, which occurs due to increased contentions and collisions in networks. To solve this, some sort of backbone like structure needs to be built, similar to the infrastructure in wired networks. To this end, literature suggests the construction of virtual backbone as the routing infrastructure of ad hoc networks.

The concept of virtual backbone was first proposed in [1]. In a network employing virtual backbone, a node in the network can either be a backbone node or not. Any non-backbone node has to be adjacent to at least one backbone node. Moreover, the set of backbone nodes has to be connected. Then, the routing path search space for each message is reduced from the whole network to the set of backbone nodes [2]. Routing messages are not broadcast to all the nodes. Instead backbone nodes alone exchange the routing messages. Whenever a nonbackbone node wants to communicate to a destination node, it forwards the message to a neighbour backbone node. The backbone nodes in turn send the message to the destination node.

Optimized Link State Routing (OLSR) protocol is one such protocol that relies on virtual backbone structure for routing. It is a proactive routing protocol that uses Multipoint Relay (MPR) set to construct the virtual backbone. The performance of the protocol is largely dependent upon the MPR set. Existing research has, however, identified various issues in the MPR selection scheme of OLSR protocol that needs improvement. An attractive alternative to MPR is Connected Dominating Set (CDS) which is a well-known solution for constructing virtual backbone [3].

CDS can be used to replace MPR set to construct virtual backbone in OLSR protocol. However, in networks that witness frequent node mobility, node failures and link failures, even the virtual backbone constructed using CDS can fast become obsolete, as it offers only 1-connected 1-domination. In the event of failure of even a single backbone node, the virtual backbone is prone to break which ultimately breaks the network. Hence, it is essential that a fault-tolerant virtual backbone is constructed which can withstand node and link failures. For this, k-Connected m-Dominating Set (kmCDS) could be employed.

In this direction, the present paper proposes Fault-Tolerant Optimized Link State Routing (FT-IOLSR) protocol that uses kmCDS to construct fault-tolerant virtual backbone, effectively replacing MPR set in the OLSR protocol. The performance of the FT-IOLSR protocol is examined in relation to that of the OLSR protocol through simulations.

The rest of the paper is organized as follows. Section 2 presents an overview of the OLSR protocol followed by the concept of CDS. Section 3 summarizes the prior research work related to the construction of kmCDS. The formation of fault-tolerant virtual backbone in FT-IOLSR protocol is elaborated in section 4. The simulation results comparing the performance of FT-IOLSR protocol in relation to that of the OLSR protocol are presented in section 5. Section 6 concludes the paper.

• II.    Overview

In this section, OLSR protocol is discussed briefly. The definitions and the basic concepts of CDS are also presented.

• A.    Optimized Link State Routing (OLSR) Protocol

  OLSR is a proactive routing protocol for mobile ad hoc networks described in RFC 3626 [4]. OLSR protocol uses MPR set as the virtual backbone. Each node selects a set of nodes in the symmetric 1-hop neighbourhood to retransmit its messages. These set of selected neighbour nodes are called the MPR set of the node. The MPR nodes alone forward the control traffic. The nodes which are not part of the MPR set only receive and process broadcast messages. They do not retransmit broadcast messages. The MPR set is chosen in such a way that it covers all the symmetric strict 2-hop nodes.

Multipoint Relay Selector set of a node contains information about the set of neighbours that have selected the node as MPR. This information is gathered via periodic HELLO messages received from the neighbours. HELLO messages take care of three tasks: link sensing, neighbour detection and MPR selection signaling. Nodes broadcast HELLO messages to their neighbours and the HELLO messages are never forwarded [4].

Each and every MPR node broadcasts topology control (TC) messages to create the topology information base. The TC messages are flooded to all the network nodes and the information transmitted via the TC messages enables the nodes to populate their routing table [4]. The routing table enables the nodes to route data to other nodes in the network.

• B.    Connected Dominating Set (CDS)

The history of dominating set can be traced back to 1850’s [5]. Given a graph G = (V,E), a Dominating Set

(DS) of G is a subset C ⊂ V such that each node either belongs to C or is adjacent to at least one node in C [6]. In other words, a Dominating Set of a graph G = (V,E) is a set of nodes V ′ such that ∀ (v,w) ∈ E, v ∈ V ′ or w ∈ V ′ [7].

A Dominating Set is connected if there exist a path between any two nodes in the set and the path only consists of the nodes in the set [8]. A Connected Dominating Set of G = (V,E) is a Dominating Set of G such that the subgraph of G induced by the nodes in this set is connected. The nodes in a CDS are called the dominators. The nodes other than the dominators are called the dominatees. Each dominatee is dominated by a dominator [9]. The size of a CDS is equal to the number of dominators [7]. Among all CDSs of graph G, the one with minimum cardinality is called a Minimum Connected Dominating Set (MCDS) [10].

In CDS based routing, the dominator nodes alone maintain the routing information. A dominatee node in order to send a message to another dominatee, will send it to its dominator. Then the search space for the route is reduced only within the CDS. That is, in a CDS C, the nodes in C can communicate with any other node in the same set without using nodes in V – C [11]. When the message reaches the destination’s dominator, the message is delivered to the destination via the said dominator [12].

• III.    Related Work

Constructing k-Connected k-Dominating Set (k-CDS), as the backbone of wireless networks, was first proposed in [13]. Four protocols have been proposed to construct a k-CDS, all of which are localized algorithms that depend on neighbourhood information alone. Fault-tolerant dominating set is investigated in [14]. The authors focus on k-fold dominating set in two network models. The authors in [15] focus on minimum m-connected k-tuple dominating set problem.

The concept of kmCDS has been studied in [16] and two approximation algorithms have been proposed. The authors in [17] present a centralized algorithm and a distributed deterministic algorithm to build kmCDS for general k and m. The problem of distributively constructing the k-dominating sets is examined in [18] and an incremental distributed algorithm for the same has been presented. In [3], the authors focus on fault-tolerant CDS problem in wireless networks. An approximation algorithm for kmCDS is presented.

Constructing kmCDS for general k and m has been examined in [19]. A centralized algorithm and a distributed local decision algorithm are proposed. The authors in [20] provide a Connecting Dominating Set Augmentation algorithm to form a 2-connected virtual backbone that can resist the failure of one wireless node. Constructing a connected k-dominating set (1-k-CDS) is examined in [21]. In [22], the authors propose a decentralized algorithm for constructing 2-Connected 1-Dominating Set (2-1-CDS).

2-Connected m-Dominating Set in ad hoc networks has been studied in [23]. The proposed decentralized algorithm creates a robust backbone in ad hoc networks and is adaptable to mobile environments. In [6], the authors provide three algorithms to construct kmCDS for general k and m in wireless networks. Constructing quality fault-tolerant virtual backbone in wireless networks has been examined in [24]. The author in [25] has investigated the problem of finding small k-dominating sets in general graphs.

In [26], a greedy algorithm that constructs a minimum 1-m-CDS is presented. The authors in [27] present an integer programming formulation and an optimal algorithm to achieve routing flexibility and faulttolerance. In [28], an approximation algorithm for minimum 3-Connected m-Dominating Set problem for m ≥ 3 using Tutte’s decomposition technique has been provided.

• IV.    Fault-Tolerant Improved Optimized Link State Routing (FT-IOLSR) Protocol

This section discusses kmCDS, the HELLO message format and the functioning of FT-IOLSR protocol.

• A.    k-Connected m-Dominating Set (kmCDS)

A CDS preserves only 1-connectivity. Because of this, many dominatees may be attached to only one dominator. Under these conditions, the failure of any one dominator results in breakage in the virtual backbone connectivity. This seriously impedes the message delivery capability of the routing protocol and ultimately degrades its performance. Whereas, in a kmCDS, the requirement of k-connectivity guarantees that, between any pair of nodes in a CDS, there exist at least k different paths. With k-connectivity, communication will not be disrupted even when up to k - 1 paths fail. k-connected virtual backbones also provide multi-path redundancy for load balancing and transmission error tolerance [6, 17, 19].

Definition 1: k-vertex connected or k-connected

A graph G is said to be k-vertex connected or k-connected if for each pair of vertices there exists at least k mutually independent paths connecting them. In other words, the graph G is still connected even after the removal of any k – 1 vertices from G [29].

The requirement of m-domination takes care of faulttolerance and robustness of dominatee nodes which are not part of the CDS. The m-domination constraint ensures that every dominatee node has at least m neighbour dominators in a CDS. Therefore, one dominatee node can still be connected with the CDS even when up to its m -1 dominator neighbours fail [6, 17, 19].

Definition 2: m-dominating set

An m-dominating set D m is a set D m ⊂ V such that every vertex in V \ D_m is dominated by at least m vertices in D m [29].

Thus, with a kmCDS, every dominatee node can tolerate up to m – 1 faults on its dominators and the virtual backbone can tolerate up to k – 1 faults [26].

Definition 3: k-Connected m-Dominating Set

A set C ⊂ V is a k-Connected m-Dominating Set (kmCDS) of graph G(V,E) if the induced subgraph G’(C,E’) is k-vertex connected and the set C is also an m-dominating set of G [29].

The proposed FT-IOLSR protocol uses kmCDS to construct a fault-tolerant virtual backbone.

• B.    HELLO Message Format

HELLO messages, which are never forwarded, are primarily used for neighbour detection. To gather the required data about neighbours, for constructing fault-tolerant virtual backbone, fields have been added to the HELLO message format [4] of the OLSR protocol. The structure of the HELLO message used in FT-IOLSR protocol is shown in Fig. 1. The new fields that are added are Weight, Colour, NodeID, NodeConnectCount and the list of NodeConnectIDs. Weight of a node is a function used to calculate the importance of the node based on its degree, where degree refers to the number of neighbour nodes. Colour of a node could be white or black denoting that the node is a dominatee or a dominator respectively. NodeID field denotes a unique number used for identification of the node.

8 bits             8 bits             8 bits               8 bits

, 4        ► 4        ► 4        ► 4        »

Weight    1    Colour	NodeID	Reserved
Reserved	HTime	Willingness
NodeConnectCount	NodeConnectID
NodeConnectID	NodeConnectID
Link Code      Reserved	Link Message Size
Neighbour Interface Address
Neighbour Interface Address
Link Code      Reserved	Link Message Size
Neighbour Interface Address
Neighbour Interface Address

Fig.1. HELLO Message Format of FT-IOLSR Protocol

After constructing CDS, each node determines whether kmCDS criterion is satisfied in its neighbourhood. If not, the node determines the list of nodes that need to be upgraded as dominators to satisfy the criterion for kmCDS. The IDs of these chosen nodes are sent to the neighbour nodes using the NodeConnectIDs field of the HELLO message. The count of this list of node IDs is sent in the NodeConnectCount field of the HELLO message. Whenever a request from neighbour nodes, for the current node to become a dominator node, is received through HELLO messages, the current node upgrades itself to become a dominator.

• C.    Functioning of FT-IOLSR protocol

The protocol starts with forming a Minimum Connected Dominating set (MCDS) which is 1-connected and 1-dominating, using any of the existing MCDS construction algorithms. This is followed by augmenting the MCDS to become 1-Connected m-Dominating set (1- m-CDS), so that the virtual backbone becomes m-dominating. Next, the protocol makes the virtual backbone to be k-connected, so that the virtual backbone becomes k-connected m-dominating. As part of this process, whenever a node gets a request for becoming a dominator from other nodes, in order to satisfy k-connected m-dominating criterion, the node upgrades itself to become a dominator. Algorithm 1 depicts the overall functioning of the FT-IOLSR protocol.

Algorithm 1. FT-IOLSR_CDS()

• 1.    Construct the MCDS virtual backbone

• 2.    Make the virtual backbone to be 1-connected m-dominating using algorithm FT-IOLSR_mCDS()

• 3.    Augment the CDS in step 2 to be k-connected using algorithm FT-IOLSR_kmCDS()

• 4.    Nodes become dominators using algorithm FT-IOLSR_kmCDSUpdation(), on receiving request from neighbour nodes through HELLO messages

• (i)    1-Connected m-dominating virtual backbone

Each dominatee node determines its number of 1-hop neighbour nodes and out of these, the number of dominator nodes is found out. The node then verifies whether it is connected to m number of dominator nodes to satisfy the m-dominating criterion. If the m-dominating criterion is satisfied, no further action on the part of the node is necessary.

On the other hand, if the node is connected to less than m number of dominators, additional nodes need to be made dominators. For this, the node selects the required number of neighbour dominatee nodes, with respect to the node’s weight in descending order. Weight of a node is calculated by finding the degree of a node, which refers to the number of its neighbour nodes. If the required number of nodes are unavailable, the available dominatee neighbour nodes are selected. The selected neighbour nodes are then requested to become dominators. The node sends this request in the next outgoing HELLO message. Algorithm 2 depicts the m-dominating process.

Algorithm 2. FT-IOLSR_mCDS()

• 1.    N(u) is the set of 1-hop neighbours reachable by a

• 2.    t = number of nodes in {N(u)} and n = number of nodes in

• 3.    m denotes the m-domination parameter

• 4.     if (n >= m) then

• 5.         1-Connected m-Dominating criterion is satisfied

• 6.     end if

• 7.     if (n < m) then

• 8.       Find nr, the number of dominatee neighbournodes

• 9.       r represents the shortage in m-domination

• 10.        if (nr <= r) then

• 11.         Request the remaining nodes in the set

• 12.         else

• 13.         Request the set of top r neighbour nodes in

• 14.        end if

• 15.    end if

dominatee node u

{N(u) ∩ MCDS}

{N(u) - {N(u) ∩ MCDS}} to become dominators

the set {N(u) - {N(u) ∩ MCDS}}, with respect to weight in descending order, to become dominators

• (ii)    k-connected m-dominating virtual backbone

• 4.

• 5.

• 6.

• 7.

• 8.

To make the virtual backbone k-connected, each dominator node finds the number of mutually independent paths between itself and each of its neighbour dominator nodes. It then determines whether the available number of paths to each of its neighbour dominator nodes is greater than or equal to k. If so, the k-connected criterion is satisfied and no change to the virtual backbone needs to be made by the dominator node. For the neighbour dominator nodes, for which this criterion is not satisfied, the dominator node determines the other viable paths through which the k-connected criterion can be satisfied. These paths should be mutually independent of the already available paths connecting the node under consideration with a given neighbour dominator node. Also, the paths with shortest length should be given preference.

If the available paths are less than the number of paths required to satisfy the k-connected criterion, then all the paths are chosen. If the available paths are more than the required number of paths to satisfy the k-connected criterion, the required number of paths are chosen among them, taking shortest path as the selection criterion. The dominatee nodes on these newly determined paths are requested to become dominators in the next outgoing HELLO message. The process of making the virtual backbone k-connected is depicted in Algorithm 3.

Algorithm 3. FT-IOLSR _ kmCDS()

u is the current dominator node and k denotes the k-connectivity parameter

Ndom(u) is the set of neighbour dominator nodes reachable from u

Compute mutually independent paths Pdom(i) between u and i passing through only dominator nodes, where i ∈ Ndom(u) ndom(i) = number of paths in Pdom(i) if (ndom(i) >= k) then k-Connected m-Dominating criterion is satisfied else xdom(i) denotes the set of nodes used to find

Pdom(i)

Determine all the mutually independent paths Pnewdom(i) between node u and i through nodes excluding the ones in xdom(i), giving preference to shortest paths nnewdom(i) = number of paths in Pnewdom(i) krem(i) = k – ndom(i)

if (nnewdom(i) <= krem(i)) then

Use all the paths in Pnewdom(i)

Find the largest subset of nodes w in

Pnewdom(i) such that {w ∩ CDS} = {} and request the nodes in w to become dominators else

Use top krem(i) paths from Pnewdom(i) with respect to the path length in increasing order, denoted by Pselnewdom(i)

Find the largest subset of nodes w in

Pselnewdom(i) such that {w ∩ CDS} = {} and request the nodes in w to become dominators end if end if

• (iii)    kmCDS updation

A node may be requested by the neighbour nodes to become a dominator to form kmCDS. These requests are transmitted by the neighbour nodes using HELLO messages. Whenever a node receives a HELLO message, the list of IDs of the nodes which have been requested to become dominators is verified to determine whether the node’s ID is part of it. If so and if the current node’s ID is less than the node ID of the sender of the HELLO message, the node becomes a dominator, provided it is a dominatee at that point of time. If not, no action needs to be taken on the part of the node. The steps of the updation process are given in Algorithm 4.

Algorithm 4. FT-IOLSR_kmCDSUpdation()

• 1.     u denotes the current node

• 2.    x is the originator of the HELLO message

• 3.     C is the set of dominator nodes

• 4.    v denotes the set of nodes received through HELLO

• 5.     if (u ⊂ v) and (uid < xid) then

• 6.       C = C U {u}

• 7.     else

• 8.         Discard the received list of nodes

• 9.     end if

message in NodeConnectID field for becoming dominators

• V.    Simulation

The simulation environment and the simulation results are presented in this section.

• A.    Simulation Environment

  Using the NS-3 simulator [30], the performance of FT-IOLSR and OLSR protocols is assessed. Simulations have been carried out for a network consisting of 50 nodes which are spread over an area of 1250m x 1250m. Random waypoint mobility model is used with node speed varied as 5, 10 and 15 m/s. The pause time has been set as 2 seconds and 5 seconds. Simulation is run for a total of 500 seconds.

FT-IOLSR protocol and OLSR protocol have been assessed by studying the impact of mobility on packet delivery ratio (PDR), with various node speed and pause time combinations. The performance of the FT-IOLSR protocol is also assessed under varying node speed keeping pause time constant and also under varying pause time keeping the node speed constant. Also, the effect of the network size on the performance of both the protocols is examined. Further, the impact of connectivity factor and the impact of domination factor on the performance of FT-IOLSR protocol is examined.

• B.    Simulation Results

• (i)    Impact of mobility

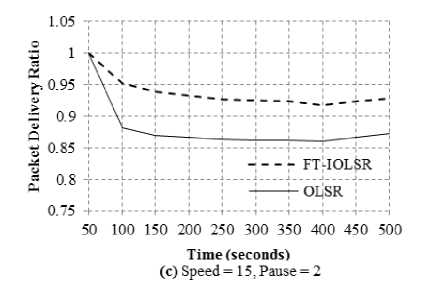
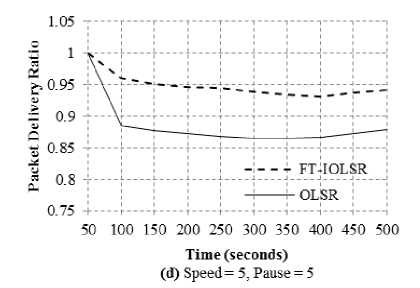
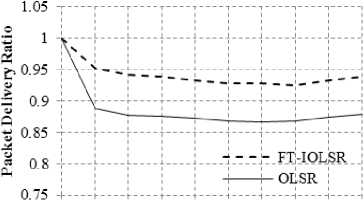
Fig. 2(a) to 2(f) reflect the PDR of FT-IOLSR and OLSR protocols for various combinations of node speed and pause time. The node speed is varied as 5, 10 and 15 m/s and the pause time is set as 2 seconds and 5 seconds.

It is clearly evident from the figures that, for different node speed and pause time combinations, PDR of FT-IOLSR protocol is substantially higher than that of the OLSR protocol. This is because, due to mobility, nodes get detached from one part of the network and attach themselves to another part of the network. Because of this, the already available routes to different destinations may become obsolete and the packets do not reach their destinations, causing packet loss. The movement of the nodes belonging to the MPR set in the OLSR protocol affects its performance, as non-MPR set nodes may not be in the vicinity of any node belonging to the MPR set. Also the connectivity among the nodes of the MPR set may be lost due to node mobility.

The FT-IOLSR protocol provides a solution to this by employing fault-tolerant CDS where the virtual backbone is k-connected m-dominating. This, as already elaborated, provides fault-tolerance up to k – 1 path failures and m – 1 dominator failures. Because of this, the k-connected m-dominating virtual backbone formed by the FT-IOLSR protocol is able to withstand disconnections owing to node mobility. As a result, the packet delivery is better in FT-IOLSR protocol and PDR is comparatively higher than that of the OLSR protocol.

• (a)    Impact of varying node speed and constant pause time

The impact of varying node speed, keeping the pause time constant, on the performance of the FT-IOLSR protocol is next examined. Fig. 3(a) and 3(b) show the PDR of FT-IOLSR with varying node speed keeping the pause time constant as 2 seconds and 5 seconds respectively. The node speed is varied as 5 m/s, 10 m/s and 15 m/s.

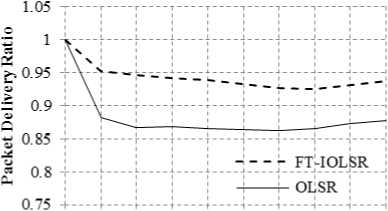
50 100 150 200 250 300 350 400 450 500

Time (seconds) (a) Speed = 5. Pause = 2

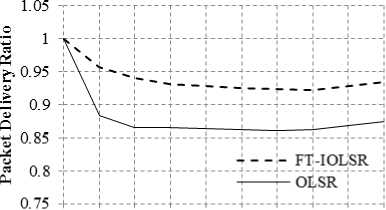
50 100 150 200 250 300 350 400 450 500

Time (seconds) (b) Speed = 10, Pause = 2

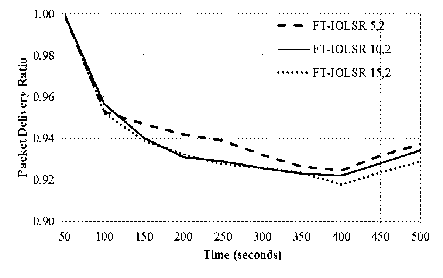
Fig.3(a). Impact of Varying Node Speed with 2 Seconds Pause Time

50 100 150 200 250 300 350 400 450 500

Time (seconds) (e) Speed = 10. Pause = 5

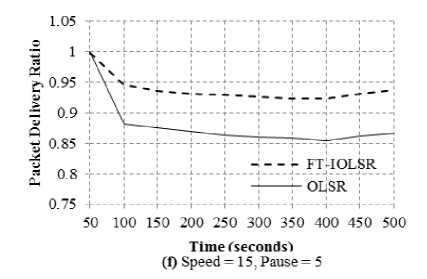
Fig.2. PDR of FT-IOLSR and OLSR Protocol

Fig.3(b). Impact of Varying Node Speed with 5 Seconds Pause Time

FT-IOLSR protocol provides better PDR at node speed of 5 m/s as compared to 10 m/s and 15 m/s. This is observed in both the cases of 2 seconds and 5 seconds pause time. There is gradual decline in PDR as the node speed is increased to 10 m/s and 15 m/s. At lower speed, there are fewer disconnections owing to mobility, and hence improved PDR is observed. It is evident that the PDR gradually decreases with increase in speed in both the cases of pause time under consideration.

• (b)    Impact of varying pause time and constant node speed

The performance of the FT-IOLSR protocol is examined with respect to varying pause time keeping the node speed as constant. The results of the PDR are as shown in Fig. 4(a) to 4(c), where the node speed is 5 m/s, 10 m/s and 15 m/s respectively, with pause time being set as 2 seconds and 5 seconds. The results in these figures indicate that there is an increase in PDR when the pause time is increased, for node speed of 5 m/s and 10 m/s. However, as the node speed increases to 15 m/s, the improvement is very minimal. It can be inferred that at lower node speeds, the increase in pause time has a positive effect on the PDR.

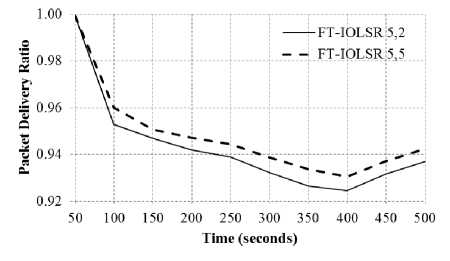
Fig.4(a). Impact of Varying Pause Time with 5 m/s Node Speed

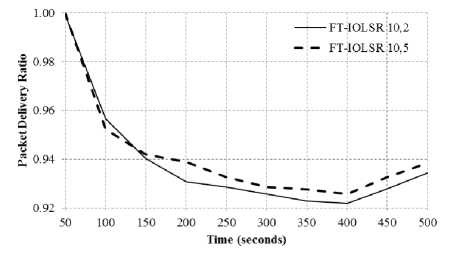
Fig.4(b). Impact of Varying Pause Time with 10 m/s Node Speed

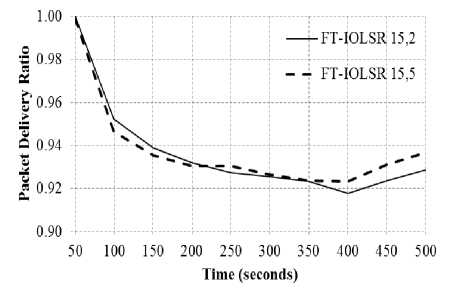
Fig.4(c). Impact of Varying Pause Time with 15 m/s Node Speed

A comparative chart illustrating the performance of the FT-IOLSR protocol in terms of PDR for various combinations of node speed and pause time is shown in Fig. 5. From the figure, it is inferred that, as the node speed increases, the PDR decreases, whereas with increase in pause time the PDR increases.

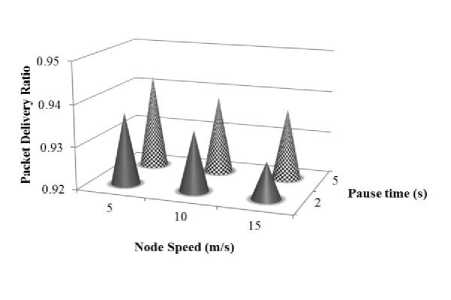
Fig.5. PDR of FT-IOLSR Protocol for Various Node Speed and Pause Time Combinations

• (ii)    Impact of network size

The effect of network size on the PDR achieved by FT-IOLSR protocol and OLSR protocol is examined. The results are shown in Fig. 6, where the network size is varied as 25, 50, 75 and 100 nodes. It is observed that, as the number of nodes in the network increases, the PDR of both the protocols increases. There is comparatively substantial improvement in PDR in the case of 25 and 50 nodes in both FT-IOLSR and OLSR protocols. Then, for the other two increments of 25 nodes, there is gradual increase in PDR.

The increase in PDR can be attributed to the increase in node density, as a result of increase in network size. Increased node density leads to more connectivity in the network and hence, better packet delivery can be achieved with increase in network size. Further, it is evident that FT-IOLSR protocol consistently performs better than the OLSR protocol due to its fault-tolerance capability.

• (iii)    Impact of connectivity factor

Next the performance of the FT-IOLSR protocol is evaluated under varying connectivity factor and the results are shown in Fig. 7. Connectivity factor is described by the k value which is varied from 1 to 4 and the dominating factor is set as 2.

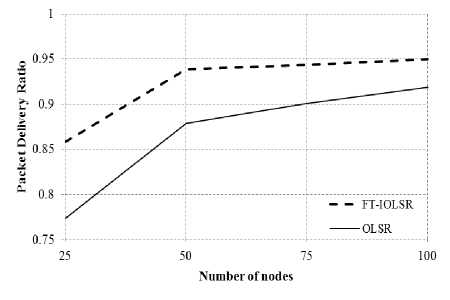
Fig.6. Impact of Network Size

It is observed that as the connectivity factor increases from 1 to 3, there is gradual improvement in the PDR. But, as the connectivity factor gets increased to 4, substantial improvement in PDR is observed. It is therefore inferred that with increase in connectivity factor, the protocol provides better PDR.

As the connectivity factor increases, more mutually independent paths are available between any two dominators and the network is therefore able to withstand multiple dominator failures. This results in successful delivery of more number of packets. Hence, virtual backbones with higher connectivity factor perform better as compared to those with lower k-connectivity values.

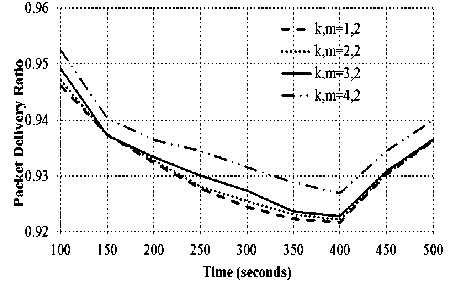
Fig.7. Impact of Connectivity Factor on FT-IOLSR Protocol

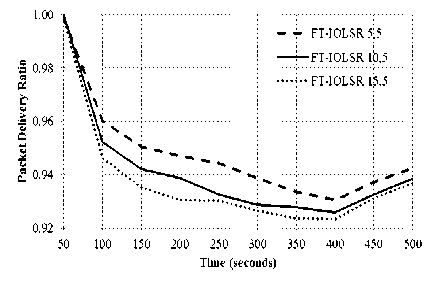
• (iv)    Impact of domination factor

PDR achieved by the FT-IOLSR protocol for varying domination factor is shown in Fig. 8. Connectivity factor k is set as 2, whereas the domination factor m is varied from 1 to 4. The results indicate that increase in domination factor leads to improved PDR. When the domination factor is increased, the number of dominators to which a dominatee is connected increases and therefore, a dominatee node is able to survive multiple dominator failures. This in turn, substantially improves the fault-tolerance capability of the network and hence, an improvement in PDR is observed.

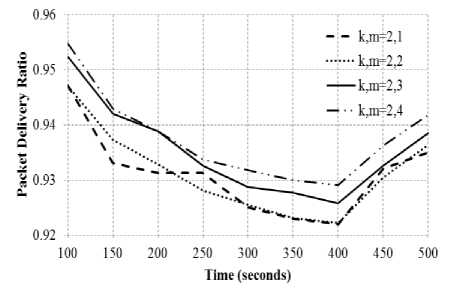
Fig.8. Impact of Domination Factor on FT-IOLSR Protocol

• VI.    Conclusion

The proposed FT-IOLSR protocol used kmCDS to construct the fault-tolerant virtual backbone that can withstand up to m – 1 dominator node failures and up to k – 1 path failures. It effectively replaced the MPR set used in the OLSR protocol. Simulations were carried out comparing the performance of the FT-IOLSR protocol against OLSR protocol. The performance of the FT-IOLSR protocol has been assessed in terms of PDR under varying mobility, network size, domination factor and connectivity factor. The simulation results indicate that the FT-IOLSR protocol performed better under various combinations of node speed and pause time and varying network size. Further, with increase in domination factor and connectivity factor, the protocol exhibited improved performance.