A feature selection based ensemble classification framework for software defect prediction
Автор: Ahmed Iqbal, Shabib Aftab, Israr Ullah, Muhammad Salman Bashir, Muhammad Anwaar Saeed
Журнал: International Journal of Modern Education and Computer Science @ijmecs
Статья в выпуске: 9 vol.11, 2019 года.
Бесплатный доступ
Software defect prediction is one of the emerging research areas of software engineering. The prediction of defects at early stage of development process can produce high quality software at lower cost. This research contributes by presenting a feature selection based ensemble classification framework which consists of four stages: 1) Dataset selection, 2) Feature Selection, 3) Classification, and 4) Results. The proposed framework is implemented from two dimensions, one with feature selection and second without feature selection. The performance is evaluated through various measures including: Precision, Recall, F-measure, Accuracy, MCC and ROC. 12 Cleaned publically available NASA datasets are used for experiments. The results of both the dimensions of proposed framework are compared with the other widely used classification techniques such as: “Naïve Bayes (NB), Multi-Layer Perceptron (MLP). Radial Basis Function (RBF), Support Vector Machine (SVM), K Nearest Neighbor (KNN), kStar (K*), One Rule (OneR), PART, Decision Tree (DT), and Random Forest (RF)”. Results reflect that the proposed framework outperformed other classification techniques in some of the used datasets however class imbalance issue could not be fully resolved.
Ensemble Classifier, Hybrid Classifier, Random Forest, Software Defect Prediction, Feature Selection
Короткий адрес: https://sciup.org/15016880
IDR: 15016880 | DOI: 10.5815/ijmecs.2019.09.06
Текст научной статьи A feature selection based ensemble classification framework for software defect prediction
Published Online September 2019 in MECS DOI: 10.5815/ijmecs.2019.09.06
Today, the production of high quality software at lower cost is challenging due to the large size and high complexity of required systems [1,2], [23]. However this issue can be resolved if we can predict about the particular software modules in advance, where defects are more likely to occur in future [3], [10]. The process of predicting a defective module is known as software defect prediction in which we predict the future defects at the early stages of software development life cycle (before the testing). It is considered as one of the challenging tasks of quality assurance process. Identification of defective modules at the early stage is vital as the cost of correction increases at later stages of development life cycle. Software metrics extracted from historical software data is used to predict the defective modules [29,30,31,32]. Machine learning techniques have been proved as a promising way for effective and efficient software defect prediction. These techniques are categories as 1) supervised, 2) un-supervised, and 3) hybrid. The supervised technique needs a pre-classified (training data) in order to train the classifier. During training the rules are developed which are further used to classify the unseen data (test data). In unsupervised techniques no training data is needed as these techniques use particular algorithm to identify the classes and maintain. The hybrid approach integrates the both (supervised and un-supervised). This paper proposed a feature selection based ensemble classification framework for software defect prediction. The framework is implemented from two dimensions, one with the feature selection and second without the feature selection, so that the difference of results in both dimensions can be analyzed and discussed. Each dimension further used two techniques Bagging and Boosting with Random Forest. Performance evaluation is performed from various measures such as: Precision, Recall, F-measure, Accuracy, MCC and ROC. Clean version of 12 publically available NASA datasets are used in this research including: “CM1, JM1, KC1, KC3, MC1, MC2, MW1, PC1, PC2, PC3, PC4 and PC5”. The results of the proposed framework are also compared with other widely used supervised classification techniques such as: “Naïve Bayes (NB), Multi-Layer Perceptron (MLP). Radial Basis Function (RBF), Support Vector Machine (SVM), K Nearest Neighbor (KNN), kStar (K*), One Rule (OneR), PART, Decision Tree (DT), and Random Forest (RF)”. According to results the proposed framework showed higher performance in some of the used datasets but the class imbalance problem is not fully resolved. The class imbalance issue in software defect datasets is one of the main reason of lower and biased performance of classifiers [22,23].
-
II. Related Work
Many researchers have used machine learning techniques to resolve the classification problems in various areas including: sentiment analysis
[11,12,13,14,15,16], network intrusion detection [17] “in press”[18],[19], rainfall prediction [20,21], and software defect prediction [10], [29] etc.. Some selected studies regarding the software defect predictions are discussed here briefly. In [10] the researchers compared the performance of various supervised machine learning techniques on software defect prediction and used 12 NASA datasets for experiments. The authors have highlighted that Accuracy and ROC did not show any reaction on class imbalance issue however Precision, Recall, F-Measure and MCC reacted on this issue with a symbol of “?” in results. In [24], the researchers used six classification techniques for software defect prediction and used the data of 27 academic projects for experiment. The used techniques are: Discriminant Analysis, Principal Component Analysis (PCA), Logistic Regression (LR), Logical Classification, Holographic Networks, and Layered Neural Networks model. Back-propagation learning technique was used to train ANN. Performance evaluation was performed by using following measures: Verification Cost, Predictive
Validity, Achieved Quality and Misclassification Rate. The results reflected that, no classification technique performed better on software defect prediction in the experiment. In [25] the researchers predicted the software defects by using SVM and compared the performance with other widely used prediction techniques including: Logistic Regression (LR), K-Nearest Neighbors (KNN), Decision Trees, Multilayer Perceptron (MLP), Bayesian Belief Networks (BBN), Radial Basis Function (RBF), Random Forest (RF), and Naïve Bayes, (NB). For experiments, NASA datasets are used including: PC1, CM1, KC1 and KC3. According to results SVM outperformed some of the other classification techniques. In [26] the researchers explored and discussed the significance of particular software metrics for the prediction of software defects. They identified the significant software metrics with the help of ANN after training with historical data. After that the extracted and shortlisted metrics were used to predict the software defects through another ANN model. The performance of the proposed technique was compared with Gaussian kernel SVM. JM1 dataset from NASA MDP repository was used for experiment. According to results the SVM performed better than ANN in binary defect classification. Researchers in [27] proposed a technique for software defect prediction which includes a novel Artificial Bee Colony (ABC) algorithm with Artificial Neural Network in order to find the optimal weights. For experiment, five publically available datasets were used from NASA MDP repository and the results reflected the higher results of proposed technique as compared to other classification techniques. In [28], the researchers introduced an approach which consists of Hybrid Genetic algorithm and Deep Neural Network. Hybrid Genetic algorithm is used for the selection and optimization of features whereas Deep Neural Network is used for classification by focusing on the selected features. The experiments were carried out on the PROMISE datasets and the results showed the higher performance of proposed approach as compared to other defect prediction techniques.
-
III. MAterials and Methods
This research proposes a feature selection based ensemble classification framework to predict the software defects.
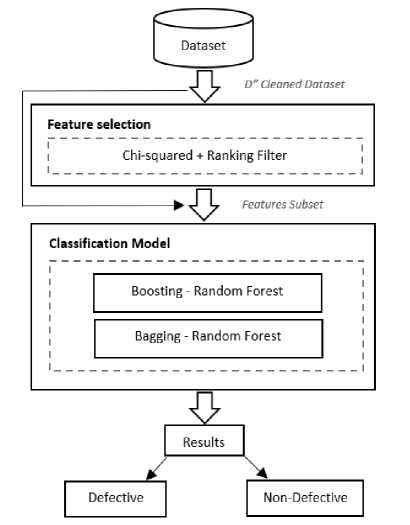
Fig.1. Proposed Classification Framework.
The proposed framework (Fig. 1) consists of four stages: 1) Dataset selection, 2) Feature Selection, 3) Classification, and 4) Results. The framework is implemented in two dimensions, in first, the feature selection stage is skipped and datasets are directly given to the ensemble classifiers however in second dimension the datasets gone through the feature selection stage. The performance of both the dimensions of proposed framework is compared with other widely used classifiers such as: “Naïve Bayes (NB), Multi-Layer Perceptron (MLP), Radial Basis Function (RBF), Support Vector Machine (SVM), K Nearest Neighbor (kNN), kStar (K*), One Rule (OneR), PART, Decision Tree (DT), and Random Forest (RF)”. All the experiments are performed in WEKA [5], which is the widely used data mining tools. It is developed in Java language at the University of Waikato, New Zealand. It is widely accepted due to its portability, General Public License and ease of use.
Dataset selection is the first stage of proposed framework. Twelve publically available cleaned NASA datasets are used in this research for experiment. The datasets include: “CM1, JM1, KC1, KC3, MC1, MC2, MW1, PC1, PC2, PC3, PC4 and PC5 (Table 2)”. Each dataset belongs to a particular NASA’s software system, and consists of various quality metrics in the form of attributes along with known output class. The output class is also known as target class and is predicted on the basis of other available attributes. The target/output class is known as dependent attribute whereas other attributes which are used to predict the dependent attribute are known as independent attributes. The datasets used in this research included dependent attribute having values either “Y” or “N”. “Y” reflects that the particular instance (module) is defective and “N” means it is nondefective. The researchers in [4] provided two versions of clean datasets: DS’ (“which included duplicate and inconsistent instances”) and D’’ (“which do not include duplicate and inconsistent instances”). Table 1 reflects the cleaning criteria implemented by [4]. We have used D’’ (Table 2) version in this research which is taken from [6]. These cleaned datasets are already used and discussed by [7,8,9,10].
Table 1. Cleaning Criteria [4]
|
Criterion |
Data Quality Category |
Explanation |
|
1. |
Identical cases |
“Instances that have identical values for all metrics including class label”. |
|
2. |
Inconsistent cases |
“Instances that satisfy all conditions of Case 1, but where class labels differ‘. |
|
3. |
Cases with missing values |
“Instances that contain one or more missing observations”. |
|
4. |
Cases with conflicting feature values |
“Instances that have 2 or more metric values that violate some referential integrity constraint. For example, LOC TOTAL is less than Commented LOC. However, Commented LOC is a subset of LOC TOTAL”. |
|
5. |
Cases with implausible values |
“Instances that violate some integrity constraint. For example, value of LOC=1.1”. |
Table 2. NASA Cleaned Datasets D’’ [4], [7]
|
Dataset |
Attributes |
Modules |
Defective |
NonDefective |
Defective (%) |
|
CM1 |
38 |
327 |
42 |
285 |
12.8 |
|
JM1 |
22 |
7,720 |
1,612 |
6,108 |
20.8 |
|
KC1 |
22 |
1,162 |
294 |
868 |
25.3 |
|
KC3 |
40 |
194 |
36 |
158 |
18.5 |
|
MC1 |
39 |
1952 |
36 |
1916 |
1.8 |
|
MC2 |
40 |
124 |
44 |
80 |
35.4 |
|
MW1 |
38 |
250 |
25 |
225 |
10 |
|
PC1 |
38 |
679 |
55 |
624 |
8.1 |
|
PC2 |
37 |
722 |
16 |
706 |
2.2 |
|
PC3 |
38 |
1,053 |
130 |
923 |
12.3 |
|
PC4 |
38 |
1,270 |
176 |
1094 |
13.8 |
|
PC5 |
39 |
1694 |
458 |
1236 |
27.0 |
Feature selection is the second and the most significant stage of proposed classification framework. This stage selects the optimum set of features for effective classification results. Many researchers have reported that most of the datasets only have few of the independent features which can predict the target class effectively whereas remaining features do not participate well and even can reduce the performance of classifier if not removed. We have used Chi-Square as attribute evaluator along with Ranker search method as feature selection technique.
Third stage deals with the classification with ensemble classifiers. Besides the feature selection, ensemble learning techniques have also been reported as an efficient way to improve the classification results. Bagging and Boosting are the two widely used ensemble techniques provided by Weka, which are also known as meta-learners. These techniques work by taking the base learner as argument and create a new learning algorithm by manipulating the training data. We have used Bagging and Boosting along with Random Forest as base classifier in the proposed framework.
Finally the fourth (result) stage reflects the classified modules along with the accuracy of proposed framework. The results are analyzed and discussed in detail in the next section.
-
IV. Results and Discussion
This section reflects the performance of proposed framework. The performance evaluation is performed in terms of various measures generated from confusion matrix (Fig. 2).
Actual Values Defective (Y) Non-defective (N) Defective (Y) 5 Non-defective (N) ш
TP
FP
FN
TN
Fig.2. Confusion Matrix. A confusion matrix consists of the following parameters: True Positive (TP): “Instances which are actually positive and also classified as positive”. False Positive (FP): “Instances which are actually negative but classified as positive”. False Negative (FN): “Instances which are actually positive but classified as negative”. True Negative (TN): “Instances which are actually negative and also classified as negative”. The performance of both the dimensions of proposed framework is evaluated through following measures: Precision, Recall, F-measure, Accuracy, MCC and ROC [22]. These measures are calculated from the parameters of confusion matrix as shown below. TP
Precision
=---------
(TP
+
FP
)
Re
call
=
TP
(TP
+
FN
)
Precision * Recall * 2 F-measure =------------------- (Precision + Recall)
Accuracy
=
TP
+
TN
TP
+
TN
+
FP
+
FN
AUC
=
1
+
TPr
-
FPr
MCC
=
________
TN
*
TP
-
FN
*
FP
________ 4
(
FP
+
TP
)(
FN
+
TP
)(
TN
+
FP )(TN
+
FN
)
The proposed framework classified the datasets in two dimensions 1) with feature selection and 2) without feature selection. In each dimension the Random Forest classifier is used with Bagging and Boosting techniques so there are total of four techniques in the proposed framework 1) Bagging-RF, 2) Boosting-RF, Feature Selection-Bagging-RF, 4) Feature-Selection-Boosting-RF. Each of the table which reflects the results also shows the score of other classification techniques such as: “Naïve Bayes (NB), Multi-Layer Perceptron (MLP). Radial Basis Function (RBF), Support Vector Machine (SVM), K Nearest Neighbor (KNN), kStar (K*), One Rule (OneR), PART, Decision Tree (DT), and Random Forest (RF)”. These results are taken from a published paper [10] in order to compare the performance of proposed framework. The paper [10] have used the same datasets (D’’) for experiments. The results of Precision, Recall and F-Measure of each dataset for each class (Y and N) are reflected in the tables from Table 3 to Table 14. Highest scores in each class are highlighted in bold for easy identification. Table 3. CM1 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.1670
0.2220
0.1900
N
0.9190
0.8880
0.9030
MLP
Y
0.0000
0.0000
0.0000
N
0.9040
0.9550
0.9290
RBF
Y
?
0.0000
?
N
0.9080
1.0000
0.9520
SVM
Y
?
0.0000
?
N
0.9080
1.0000
0.9520
kNN
Y
0.0670
0.1110
0.0830
N
0.9040
0.8430
0.8720
kStar
Y
0.0670
0.1110
0.0830
N
0.9040
0.8430
0.8720
OneR
Y
0.0000
0.0000
0.0000
N
0.9030
0.9440
0.9230
PART
Y
?
0.0000
?
N
0.9080
1.0000
0.9520
DT
Y
0.1180
0.2220
0.1540
N
0.9140
0.8310
0.8710
RF
Y
0.0000
0.0000
0.0000
N
0.9070
0.9890
0.9460
Boost-RF
Y
0.0000
0.0000
0.0000
N
0.9070
0.9890
0.9460
Bag-RF
Y
0.0000
0.0000
0.0000
N
0.9070
0.9890
0.9460
Boost-RF-FS
Y
0.0000
0.0000
0.0000
N
0.9070
0.9890
0.9460
Bag-RF-FS
Y
0.0000
0.0000
0.0000
N
0.9070
0.9890
0.9460
Results of CM1 datasets are given in Table 3. The table reflects that, in Precision, NB performed better in both the classes (Y and N). In Recall, NB and DT both performed better in Y class whereas RBF, SVM and PART showed better performance in N class, and finally in F-measure, NB showed better performance in Y class whereas RBF, SVM and PART performed better in N class. Table 4. JM1 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.5370
0.2260
0.3180
N
0.8230
0.9490
0.8820
MLP
Y
0.7650
0.0810
0.1460
N
0.8040
0.9930
0.8890
RBF
Y
0.6940
0.1040
0.1810
N
0.8070
0.9880
0.8890
SVM
Y
?
0.0000
?
N
0.7920
1.0000
0.8840
kNN
Y
0.3630
0.3340
0.3480
N
0.8290
0.8460
0.8370
kStar
Y
0.4030
0.3170
0.3550
N
0.8300
0.8760
0.8530
OneR
Y
0.3780
0.1510
0.2160
N
0.8070
0.9350
0.8660
PART
Y
0.8180
0.0190
0.0370
N
0.7950
0.9990
0.8850
DT
Y
0.4960
0.2680
0.3480
N
0.8280
0.9290
0.8760
RF
Y
0.5720
0.1890
0.2840
N
0.8190
0.9630
0.8850
Boost-RF
Y
0.6010
0.1970
0.2970
N
0.8210
0.9660
0.8870
Bag-RF
Y
0.6190
0.1780
0.2770
N
0.8180
0.9710
0.8880
Boost-RF-FS
Y
0.6010
0.1970
0.2970
N
0.8210
0.9660
0.8870
Bag-RF-FS
Y
0.6190
0.1780
0.2770
N
0.8180
0.9710
0.8880
Results of JM1 datasets are reflected in Table 4. In precision, PART performed better in Y class whereas kStar performed better in N class. In Recall, kNN performed better in Y class and SVM performed better in N class. In F-measure, kStar outperformed in Y class whereas MLP and RBF outperformed in N class. Table 5. KC1 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.4920
0.3370
0.4000
N
0.7950
0.8810
0.8360
MLP
Y
0.6470
0.2470
0.3580
N
0.7870
0.9540
0.8630
RBF
Y
0.7780
0.2360
0.3620
N
0.7890
0.9770
0.8730
SVM
Y
0.8000
0.0450
0.0850
N
0.7530
0.9960
0.8580
kNN
Y
0.3980
0.3930
0.3950
N
0.7930
0.7960
0.7950
kStar
Y
0.4490
0.3930
0.4190
N
0.8010
0.8350
0.8170
OneR
Y
0.4440
0.1800
0.2560
N
0.7670
0.9230
0.8380
PART
Y
0.6670
0.1570
0.2550
N
0.7710
0.9730
0.8610
DT
Y
0.5330
0.3600
0.4300
N
0.8030
0.8920
0.8450
RF
Y
0.6150
0.3600
0.4540
N
0.8080
0.9230
0.8620
Boost-RF
Y
0.5770
0.3370
0.4260
N
0.8010
0.9150
0.8550
Bag-RF
Y
0.6440
0.3260
0.4330
N
0.8030
0.9380
0.8650
Boost-RF-FS
Y
0.6350
0.3710
0.4680
N
0.8110
0.9270
0.8650
Bag-RF-FS
Y
0.6520
0.3370
0.4440
N
0.8050
0.9380
0.8670
Results of KC1 datasets are given in Table 5. It can be seen that in Precision, SVM outperformed in Y Class whereas RF showed better results in N Class. In Recall, kNN and kStar performed better in Y class whereas SVM showed better performance in N class, and finally, in F-measure, Boost-RF-FS performed better in Y and RBF outperform in N class. Table 6. KC3 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.4440
0.4000
0.4210
N
0.8780
0.8960
0.8870
MLP
Y
0.5000
0.3000
0.3750
N
0.8650
0.9380
0.9000
RBF
Y
0.0000
0.0000
0.0000
N
0.8180
0.9380
0.8740
SVM
Y
?
0.0000
?
N
0.8280
1.0000
0.9060
kNN
Y
0.3330
0.4000
0.3640
N
0.8700
0.8330
0.8510
kStar
Y
0.3000
0.3000
0.3000
N
0.8540
0.8540
0.8540
OneR
Y
0.5000
0.3000
0.3750
N
0.8650
0.9380
0.9000
PART
Y
0.2500
0.1000
0.1430
N
0.8330
0.9380
0.8820
DT
Y
0.3000
0.3000
0.3000
N
0.8540
0.8540
0.8540
RF
Y
0.2860
0.2000
0.2350
N
0.8430
0.8960
0.8690
Boost-RF
Y
0.3330
0.2000
0.2500
N
0.8460
0.9170
0.8800
Bag-RF
Y
0.4000
0.2000
0.2670
N
0.8490
0.9380
0.8910
Boost-RF-FS
Y
0.4170
0.5000
0.4550
N
0.8910
0.8540
0.8720
Bag-RF-FS
Y
0.2000
0.1000
0.1330
N
0.8300
0.9170
0.8710
Results of KC3 dataset is reflected in Table 6. It is reflected that in Precision, MLP and OneR showed highest performance in Y class whereas Boost-RF-FS. In Recall, Boost-RF-FS performed better in Y class and in N class, SVM outperformed the others. In F-measure, Boost-RF-FS performed better in Y class whereas SVM performed better in N class. Table 7. MC1 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.1560
0.3570
0.2170
N
0.9840
0.9530
0.9680
MLP
Y
?
0.0000
?
N
0.9760
1.0000
0.9880
RBF
Y
?
0.0000
?
N
0.9760
1.0000
0.9880
SVM
Y
?
0.0000
?
N
0.9760
1.0000
0.9880
kNN
Y
0.4000
0.2860
0.3330
N
0.9830
0.9900
0.9860
kStar
Y
0.2500
0.1430
0.1820
N
0.9790
0.9900
0.9840
OneR
Y
0.3330
0.1430
0.2000
N
0.9790
0.9930
0.9860
PART
Y
0.4000
0.2860
0.3330
N
0.9830
0.9900
0.9860
DT
Y
?
0.0000
?
N
0.9760
1.0000
0.9880
RF
Y
0.0000
0.0000
0.0000
N
0.9760
0.9980
0.9870
Boost-RF
Y
0.3330
0.0710
0.1180
N
0.9780
0.9970
0.9870
Bag-RF
Y
?
0.0000
?
N
0.9760
1.0000
0.9880
Boost-RF-FS
Y
0.5000
0.0710
0.1250
N
0.9780
0.9980
0.9880
Bag-RF-FS
Y
?
0.0000
?
N
0.9760
1.0000
0.9880
Results of MC1 dataset are reflected in Table 7. In Precision, Boost-RF-FS showed better performance in Y class whereas NB performed better in N class. In Recall, NB performed better in Y class whereas MLP, RBF, SVM, DT, Bag-RF and Bag-RF-FS performed better in N class. In F-Measure, kNN and PART performed better in Y class whereas MLP, RBF, SVM, DT, Bag-RF, Boost-RF-FS, and Bag-RF-FS performed better in N class. Table 8. MC2 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.8330
0.3850
0.5260
N
0.7420
0.9580
0.8360
MLP
Y
0.5000
0.5380
0.5190
N
0.7390
0.7080
0.7230
RBF
Y
0.8000
0.3080
0.4400
N
0.7190
0.9580
0.8210
SVM
Y
0.4000
0.1540
0.2220
N
0.6560
0.8750
0.7500
kNN
Y
0.6670
0.4620
0.5450
N
0.7500
0.8750
0.8080
kStar
Y
0.4000
0.3080
0.3480
N
0.6670
0.7500
0.7060
OneR
Y
0.5000
0.2310
0.3160
N
0.6770
0.8750
0.7640
PART
Y
0.7270
0.6150
0.6670
N
0.8080
0.8750
0.8400
DT
Y
0.5000
0.3850
0.4350
N
0.7040
0.7920
0.7450
RF
Y
0.5000
0.4620
0.4800
N
0.7200
0.7500
0.7350
Boost-RF
Y
0.4550
0.3850
0.4170
N
0.6920
0.7500
0.7200
Bag-RF
Y
0.5000
0.4620
0.4800
N
0.7200
0.7500
0.7350
Boost-RF-FS
Y
0.5000
0.4620
0.4800
N
0.7200
0.7500
0.7350
Bag-RF-FS
Y
0.5380
0.5380
0.5380
N
0.7500
0.7500
0.7500
Table 8 reflects the results of MC2 dataset. It can be observed that in precision, NB performed better in Y class whereas PART performed better in N class. In Recall, PART performed better in Y class and NB and RBF performed better in N class. and finally, in F-Measure, PART showed highest results in both classes.
N
0.9610
0.8920
0.9250
OneR
Y
0.3330
0.1000
0.1540
N
0.9550
0.9900
0.9720
PART
Y
0.3750
0.6000
0.4620
N
0.9790
0.9480
0.9630
DT
Y
0.3890
0.7000
0.5000
N
0.9840
0.9430
0.9630
RF
Y
0.7500
0.3000
0.4290
N
0.9650
0.9950
0.9800
Boost-RF
Y
0.6000
0.3000
0.4000
N
0.9650
0.9900
0.9770
Bag-RF
Y
1.0000
0.2000
0.3330
N
0.9600
1.0000
0.9800
Boost-RF-FS
Y
0.6000
0.3000
0.4000
N
0.9650
0.9900
0.9770
Bag-RF-FS
Y
1.0000
0.2000
0.3330
N
0.9600
1.0000
0.9800
Table 9. MW1 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.3330
0.6250
0.4350
N
0.9500
0.8510
0.8980
MLP
Y
0.5450
0.7500
0.6320
N
0.9690
0.9250
0.9470
RBF
Y
?
0.0000
?
N
0.8930
1.0000
0.9440
SVM
Y
?
0.0000
?
N
0.8930
1.0000
0.9440
kNN
Y
0.4000
0.5000
0.4440
N
0.9380
0.9100
0.9240
kStar
Y
0.1430
0.1250
0.1330
N
0.8970
0.9100
0.9040
OneR
Y
0.5000
0.1250
0.2000
N
0.9040
0.9850
0.9430
PART
Y
0.2500
0.1250
0.1670
N
0.9010
0.9550
0.9280
DT
Y
0.2500
0.1250
0.1670
N
0.9010
0.9550
0.9280
RF
Y
0.3330
0.1250
0.1820
N
0.9030
0.9700
0.9350
Boost-RF
Y
0.5000
0.2500
0.3330
N
0.9150
0.9700
0.9420
Bag-RF
Y
0.5000
0.1250
0.2000
N
0.9040
0.9850
0.9430
Boost-RF-FS
Y
0.5000
0.2500
0.3330
N
0.9150
0.9700
0.9420
Bag-RF-FS
Y
0.5000
0.1250
0.2000
N
0.9040
0.9850
0.9430
Table 9 reflects the result of MW1 dataset. It can be seen that in Precision, MLP performed better in both the classes. In Recall, MLP performed better in Y class whereas RBF and SVM performed better in in N class. In F-measure, MLP performed better in both the classes. Table 10. PC1 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.2800
0.7000
0.4000
N
0.9830
0.9070
0.9440
MLP
Y
1.0000
0.3000
0.4620
N
0.9650
1.0000
0.9820
RBF
Y
0.3330
0.1000
0.1540
N
0.9550
0.9900
0.9720
SVM
Y
?
0.0000
?
N
0.9510
1.0000
0.9750
kNN
Y
0.2730
0.3000
0.2860
N
0.9640
0.9590
0.9610
kStar
Y
0.1250
0.3000
0.1760
Results of PC1 datasets are shown in Table 10. It can be seen that in Precision, MLP, Bag-RF, Boost-RF-FS, and Bag-RF-FS performed better in Y class whereas DT performed better in N class. In Recall, NB and DT performed better in Y class whereas MLP, SVM, Bag-RF, Boost-RF-FS, and Bag-RF-FS both performed better in N class. In F-measure, DT performed better in Y class whereas MLP performed better in N class. Table 11. PC2 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.0000
0.0000
0.0000
N
0.9760
0.9670
0.9720
MLP
Y
0.0000
0.0000
0.0000
N
0.9770
0.9910
0.9840
RBF
Y
?
0.0000
?
N
0.9770
1.0000
0.9880
SVM
Y
?
0.0000
?
N
0.9770
1.0000
0.9880
kNN
Y
0.0000
0.0000
0.0000
N
0.9770
0.9910
0.9840
kStar
Y
0.1430
0.2000
0.1670
N
0.9810
0.9720
0.9760
OneR
Y
0.0000
0.0000
0.0000
N
0.9770
0.9950
0.9860
PART
Y
0.0000
0.0000
0.0000
N
0.9770
0.9910
0.9840
DT
Y
?
0.0000
?
N
0.9770
1.0000
0.9880
RF
Y
?
0.0000
?
N
0.9770
1.0000
0.9880
Boost-RF
Y
?
0.0000
?
N
0.9770
1.0000
0.9880
Bag-RF
Y
?
0.0000
?
N
0.9770
1.0000
0.9880
Boost-RF-FS
Y
0.0000
0.0000
0.0000
N
0.9770
0.9950
0.9860
Bag-RF-FS
Y
?
0.0000
?
N
0.9770
1.0000
0.9880
Results of PC2 datasets are shown in Table 11. According to results in Precision, kStar performed well in both the classes. In Recall, kStar performed well in Y class whereas RBF, SVM, DT, RF, Boost-RF, Bag-RF, and Bag-RF-FS performed well in N class. In F-measure, kStar performed well in Y class however RBF, SVM, DT, RF, Boost-RF, Bag-RF, and Bag-RF-FS performed well in N class. Table 12. PC3 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.1500
0.9070
0.2570
N
0.9290
0.1900
0.3160
MLP
Y
0.3460
0.2090
0.2610
N
0.8830
0.9380
0.9090
RBF
Y
?
0.0000
?
N
0.8640
1.0000
0.9270
SVM
Y
?
0.0000
?
N
0.8640
1.0000
0.9270
kNN
Y
0.4800
0.2790
0.3530
N
0.8930
0.9520
0.9220
kStar
Y
0.3130
0.2330
0.2670
N
0.8840
0.9190
0.9010
OneR
Y
0.6000
0.1400
0.2260
N
0.8790
0.9850
0.9290
PART
Y
?
0.0000
?
N
0.8640
1.0000
0.9270
DT
Y
0.5000
0.2790
0.3580
N
0.8940
0.9560
0.9240
RF
Y
0.6000
0.1400
0.2260
N
0.8790
0.9850
0.9290
Boost-RF
Y
0.4440
0.0930
0.1540
N
0.8730
0.9820
0.9240
Bag-RF
Y
0.5710
0.0930
0.1600
N
0.8740
0.9890
0.9280
Boost-RF-FS
Y
0.6670
0.1400
0.2310
N
0.8790
0.9890
0.9310
Bag-RF-FS
Y
0.8000
0.0930
0.1670
N
0.8750
0.9960
0.9320
Results of PC3 dataset is reflected in Table 12. It can be seen that in Precision, Bag-RF-FS performed better in Y class however NB performed better in N class. In Recall, NB performed better in Y class whereas RBF, SVM and PART performed better in N class. In F-measure, DT performed better in Y class whereas Bag-RF-FS performed better in N class. Table 13. PC4 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.4860
0.3460
0.4040
N
0.9010
0.9420
0.9210
MLP
Y
0.6760
0.4810
0.5620
N
0.9220
0.9640
0.9420
RBF
Y
0.6670
0.1540
0.2500
N
0.8810
0.9880
0.9310
SVM
Y
0.8180
0.1730
0.2860
N
0.8840
0.9940
0.9360
kNN
Y
0.4770
0.4040
0.4380
N
0.9080
0.9300
0.9190
kStar
Y
0.3330
0.3270
0.3300
N
0.8940
0.8970
0.8950
OneR
Y
0.6500
0.2500
0.3610
N
0.8920
0.9790
0.9330
PART
Y
0.4640
0.5000
0.4810
N
0.9200
0.9090
0.9140
DT
Y
0.5150
0.6730
0.5830
N
0.9460
0.9000
0.9220
RF
Y
0.7780
0.4040
0.5320
N
0.9120
0.9820
0.9460
Boost-RF
Y
0.7880
0.5000
0.6120
N
0.9250
0.9790
0.9510
Bag-RF
Y
0.8570
0.3460
0.4930
N
0.9060
0.9910
0.9460
Boost-RF-FS
Y
0.8330
0.4810
0.6100
N
0.9230
0.9850
0.9530
Bag-RF-FS
Y
0.9050
0.3650
0.5210
N
0.9080
0.9940
0.9490
Results of PC4 datasets are shown in Table 13. It can be seen that in Precision, Bag-RF-FS performed better in Y class whereas DT performed better in N class. In Recall, DT performed better in Y class whereas SVM and Bag-RF-FS performed better in N class, and finally, In F-measure, Boosting-RF performed better in Y class whereas Boosting-RF-FS performed better in N class. Table 14. PC5 Data Results
Classifier
Class
Precision
Recall
F-Measure
NB
Y
0.6760
0.1680
0.2690
N
0.7590
0.9700
0.8520
MLP
Y
0.5600
0.2040
0.2990
N
0.7620
0.9410
0.8420
RBF
Y
0.7600
0.1390
0.2350
N
0.7560
0.9840
0.8550
SVM
Y
0.8750
0.0510
0.0970
N
0.7400
0.9970
0.8500
kNN
Y
0.5000
0.4960
0.4980
N
0.8150
0.8170
0.8160
kStar
Y
0.4390
0.4230
0.4310
N
0.7900
0.8010
0.7950
OneR
Y
0.4550
0.3360
0.3870
N
0.7760
0.8520
0.8120
PART
Y
0.6460
0.2260
0.3350
N
0.7700
0.9540
0.8520
DT
Y
0.5370
0.5260
0.5310
N
0.8260
0.8330
0.8300
RF
Y
0.5880
0.3650
0.4500
N
0.7940
0.9060
0.8460
Boost-RF
Y
0.5880
0.3430
0.4330
N
0.7900
0.9110
0.8460
Bag-RF
Y
0.6430
0.3280
0.4350
N
0.7900
0.9330
0.8550
Boost-RF-FS
Y
0.5880
0.3430
0.4330
N
0.7900
0.9110
0.8460
Bag-RF-FS
Y
0.6430
0.3280
0.4350
N
0.7900
0.9330
0.8550
Results of PC5 dataset are presented in Table 14. It can be seen that in Precision, SVM performed better in Y class whereas DT performed better in N class. In Recall, DT performed better in Y class whereas SVM performed better in N Class, and finally, in F-Measure, DT performed better in Y class whereas RBF, Bagging-RF and Bagging-RF-FS outperform in N class. Table 15. Accuracy Results
Dataset
NB
MLP
RBF
SVM
kNN
kStar
OneR
PART
DT
RF
Boost-
RF
Bag-RF
Boost-
RF-FS
Bag-RF-FS
CM1
82.6531
86.7347
90.8163
90.8163
77.5510
77.5510
85.7143
90.8163
77.5510
89.7959
89.7959
89.7959
89.7959
89.7959
JM1
79.8359
80.3541
80.3972
79.1883
73.9637
75.9931
77.1589
79.4905
79.1019
80.1813
80.5699
80.6131
80.5699
80.6131
KC1
74.2120
77.3639
78.7966
75.3582
69.3410
72.2063
73.3524
76.5043
75.6447
77.9370
76.7900
78.2235
78.5100
78.5100
KC3
81.0345
82.7586
77.5862
82.7586
75.8621
75.8621
82.7586
79.3103
75.8621
77.5862
79.3103
81.0345
79.3103
77.5862
MC1
93.8567
97.6109
97.6109
97.6109
97.2696
96.9283
97.2696
97.2696
97.6109
97.4403
97.4403
97.6109
97.6109
97.6109
MC2
75.6757
64.8649
72.9730
62.1622
72.9730
59.4595
64.8649
78.3784
64.8649
64.8649
62.1622
64.8649
64.8649
67.5676
MW1
82.6667
90.6667
89.3333
89.3333
86.6667
82.6667
89.3333
86.6667
86.6667
88.0000
89.3333
89.3333
89.3333
89.3333
PC1
89.7059
96.5686
94.6078
95.0980
92.6471
86.2745
94.6078
93.1373
93.1373
96.0784
95.5882
96.0784
96.0784
96.0784
PC2
94.4700
96.7742
97.6959
97.6959
96.7742
95.3917
97.2350
96.7742
97.6959
97.6959
97.6959
97.6959
97.2350
97.6959
PC3
28.7975
83.8608
86.3924
86.3924
86.0759
82.5949
87.0253
86.3924
86.3924
87.0253
86.0759
86.7089
87.3418
87.3418
PC4
86.0892
89.7638
87.4016
88.189
85.8268
81.8898
87.9265
85.3018
86.8766
90.2887
91.3386
90.2887
91.6010
90.8136
PC5
75.3937
74.2126
75.5906
74.2126
73.0315
69.8819
71.2598
75.7874
75.0000
75.9843
75.7874
76.9685
75.7874
76.9685
Table 16. ROC Area Results
Dataset
NB
MLP
RBF
SVM
kNN
kStar
OneR
PART
DT
RF
Boost-RF
Bag-RF
Boost-RF-FS
Bag-RF-FS
CM1
0.7030
0.6340
0.7020
0.5000
0.4770
0.5380
0.4720
0.6100
0.3780
0.7610
0.7650
0.7370
0.6600
0.6830
JM1
0.6630
0.7020
0.7130
0.5000
0.5910
0.5720
0.5430
0.7140
0.6710
0.7380
0.7360
0.7460
0.7360
0.7460
KC1
0.6940
0.7360
0.7130
0.5210
0.5950
0.6510
0.5510
0.6360
0.6060
0.7510
0.7510
0.7570
0.7510
0.7500
KC3
0.7690
0.7330
0.7350
0.5000
0.617
0.5280
0.6190
0.7880
0.5700
0.8070
0.7850
0.8150
0.8340
0.8670
MC1
0.8260
0.8050
0.7810
0.5000
0.6380
0.6310
0.5680
0.6840
0.5000
0.8640
0.8350
0.8470
0.8270
0.8830
MC2
0.7950
0.7530
0.7660
0.5140
0.6680
0.5100
0.5530
0.7240
0.6150
0.6460
0.6650
0.6700
0.6460
0.6570
MW1
0.7910
0.8430
0.8080
0.5000
0.7050
0.5430
0.5550
0.3140
0.3140
0.7660
0.7260
0.7420
0.7260
0.7610
PC1
0.8790
0.7790
0.8750
0.5000
0.6290
0.6730
0.5450
0.8890
0.7180
0.8580
0.8960
0.9210
0.9240
0.9100
PC2
0.7510
0.7460
0.7240
0.5000
0.4950
0.7910
0.4980
0.6230
0.5790
0.7310
0.6560
0.7740
0.4890
0.5630
PC3
0.7730
0.7960
0.7950
0.5000
0.6160
0.7490
0.5620
0.7900
0.6640
0.8550
0.8360
0.8390
0.8500
0.8410
PC4
0.8070
0.8980
0.8620
0.5830
0.6670
0.7340
0.6140
0.7760
0.8340
0.9450
0.9450
0.9530
0.9520
0.9550
PC5
0.7250
0.7510
0.7320
0.5240
0.6570
0.6290
0.5940
0.7390
0.7030
0.8050
0.7990
0.8050
0.7990
0.8050
Table 17. MCC Results
Dataset
NB
MLP
RBF
SVM
kNN
kStar
OneR
PART
DT
RF
Boost-RF
Bag-RF
Boost-RF-FS
Bag-RF-FS
CM1
0.0970
-0.0660
?
?
-0.0370
-0.037
-0.074
?
0.0410
-0.032
-0.032
-0.032
-0.032
-0.032
JM1
0.2510
0.2060
0.2150
?
0.1860
0.2120
0.1260
0.1040
0.2520
0.2440
0.2620
0.2560
0.2620
0.2560
KC1
0.2500
0.2960
0.3470
0.1510
0.1900
0.2380
0.1470
0.2390
0.2910
0.3460
0.3090
0.3440
0.3640
0.3550
KC3
0.3090
0.2950
-0.1070
?
0.2180
0.1540
0.2950
0.0560
0.1540
0.1110
0.1450
0.1850
0.3300
0.0220
MC1
0.2080
?
?
?
0.3250
0.1740
0.2060
0.3250
?
-0.006
0.1450
?
0.1820
?
MC2
0.4440
0.2430
0.3710
0.0400
0.3740
0.0620
0.1370
0.5120
0.1890
0.2160
0.1410
0.2160
0.2160
0.2880
MW1
0.3670
0.5890
?
?
0.3730
0.0380
0.2110
0.1100
0.1100
0.1500
0.3020
0.2110
0.3020
0.2110
PC1
0.4000
0.5380
0.1610
?
0.2470
0.1280
0.1610
0.4400
0.4900
0.4590
0.4050
0.4380
0.4380
0.4380
PC2
-0.0280
-0.0150
?
?
-0.0150
0.1460
-0.010
0.0150
?
?
?
?
-0.010
?
PC3
0.0880
0.1830
?
?
0.2940
0.1730
0.2450
?
0.3040
0.2450
0.1540
0.1910
0.2650
0.2460
PC4
0.3340
0.5150
0.2790
0.3420
0.3590
0.2250
0.3520
0.3960
0.5140
0.5160
0.5840
0.5070
0.5930
0.5410
PC5
0.2450
0.2160
0.2510
0.1730
0.3140
0.2270
0.2090
0.2740
0.3610
0.3220
0.3100
0.3360
0.3100
0.3360
We have considered F-measure for analysis from Table 3 to Table 14 with ‘Yes’ class. F measure is selected as it provides the average of Precision and Recall and ‘Yes’ class predicts the probability of defective modules. It has been observed from the results of F-measure that the proposed framework outperformed only in three datasets KC1, KC3 and PC4. In Accuracy (Table 15), the proposed framework performed better in four datasets including JM1, PC3, PC4, and PC5. In remaining datasets either the result is lower or equal to one or more of the other classification techniques. It has also been noted that NB, kNN, and kStar could not be able to perform better in any of the dataset. In ROC Area, the higher performance is reflected in the following datasets: CM1, JM1, KC1, KC3, MC1, PC1, and PC4 however the results in remaining datasets shows either lower or equal performance when compared to other classification techniques. It has also been observed that RBF, SVM, kNN, OneR, PART, and DT could not be able to perform better in any of the dataset. In MCC, the proposed framework showed the higher performance in following datasets: JM1, KC1, KC3 and PC4. In remaining datasets the scores are either lower or equal, as compared to other classification techniques. It has also been noted that RBF, SVM, OneR, RF, Bag-RF, and Bag-RF-FS could not be able to perform better in any of the dataset. As discussed by [10], F- measure and MCC reacts to the issue of class imbalance however it has been observed in this study that our proposed framework could not be able to fully solve that issue either. V. Conclusion This research proposed and implemented a feature selection based ensemble classification framework. The proposed framework consisted of four stages including: 1) Dataset, 2) Feature Selection, 3) Classification, and 4) Results. Two different dimensions are used in the framework, one with feature selection and second without feature selection. Each dimension further used two ensemble techniques with Random Forest classifier: Bagging and Boosting. Performance of proposed framework is evaluated through Precision, Recall, F-measure, Accuracy, MCC and ROC. For experiments, 12 Cleaned publically available NASA datasets are used and the results of both the dimensions are compared with the other widely used classification techniques such as: “Naïve Bayes (NB), Multi-Layer Perceptron (MLP). Radial Basis Function (RBF), Support Vector Machine (SVM), K Nearest Neighbor (KNN), kStar (K*), One Rule (OneR), PART, Decision Tree (DT), and Random Forest (RF)”. Results showed that the proposed classification framework outperformed other classification techniques in some of the datasets however class imbalance issue could not be resolved, which is the main reason of lower and biased performance of classification techniques. It is suggested for future work that the resampling techniques should be included in proposed framework to resolve the class imbalance issue in datasets as well as to achieve higher performance.
Список литературы A feature selection based ensemble classification framework for software defect prediction
- S. Huda, S. Alyahya, M. M. Ali, S. Ahmad, J. Abawajy, J. Al-Dossari, and J. Yearwood, “A Framework for Software Defect Prediction and Metric Selection,” IEEE Access, vol. 6, pp. 2844–2858, 2018.
- E. Erturk and E. Akcapinar, “A comparison of some soft computing methods for software fault prediction,” Expert Syst. Appl., vol. 42, no. 4, pp. 1872–1879, 2015.
- Y. Ma, G. Luo, X. Zeng, and A. Chen, “Transfer learning for crosscompany software defect prediction,” Inf. Softw. Technol., vol. 54, no. 3, Mar. 2012.
- M. Shepperd, Q. Song, Z. Sun and C. Mair, “Data Quality: Some Comments on the NASA Software Defect Datasets,” IEEE Trans. Softw. Eng., vol. 39, pp. 1208–1215, 2013.
- I.H. Witten and E. Frank, Data Mining: Practical Machine Learning Tools and Techniques, second ed. Morgan Kaufmann, 2005.
- “NASA Defect Dataset.” [Online]. Available: https://github.com/klainfo/NASADefectDataset. [Accessed: 01-July-2019].
- B. Ghotra, S. McIntosh, and A. E. Hassan, “Revisiting the impact of classification techniques on the performance of defect prediction models,” Proc. - Int. Conf. Softw. Eng., vol. 1, pp. 789–800, 2015.
- G. Czibula, Z. Marian, and I. G. Czibula, “Software defect prediction using relational association rule mining,” Inf. Sci. (Ny)., vol. 264, pp. 260–278, 2014.
- D. Rodriguez, I. Herraiz, R. Harrison, J. Dolado, and J. C. Riquelme, “Preliminary comparison of techniques for dealing with imbalance in software defect prediction,” in Proceedings of the 18th International Conference on Evaluation and Assessment in Software Engineering. ACM, p. 43, 2014.
- A. Iqbal, S. Aftab, U. Ali, Z. Nawaz, L. Sana, M. Ahmad, and A. Husen “Performance Analysis of Machine Learning Techniques on Software Defect Prediction using NASA Datasets,” Int. J. Adv. Comput. Sci. Appl., vol. 10, no. 5, 2019.
- M. Ahmad, S. Aftab, I. Ali, and N. Hameed, “Hybrid Tools and Techniques for Sentiment Analysis: A Review,” Int. J. Multidiscip. Sci. Eng., vol. 8, no. 3, 2017.
- M. Ahmad, S. Aftab, and S. S. Muhammad, “Machine Learning Techniques for Sentiment Analysis: A Review,” Int. J. Multidiscip. Sci. Eng., vol. 8, no. 3, p. 27, 2017.
- M. Ahmad, S. Aftab, and I. Ali, “Sentiment Analysis of Tweets using SVM,” Int. J. Comput. Appl., vol. 177, no. 5, pp. 25–29, 2017.
- M. Ahmad and S. Aftab, “Analyzing the Performance of SVM for Polarity Detection with Different Datasets,” Int. J. Mod. Educ. Comput. Sci., vol. 9, no. 10, pp. 29–36, 2017.
- M. Ahmad, S. Aftab, M. S. Bashir, N. Hameed, I. Ali, and Z. Nawaz, “SVM Optimization for Sentiment Analysis,” Int. J. Adv. Comput. Sci. Appl., vol. 9, no. 4, 2018.
- M. Ahmad, S. Aftab, M. S. Bashir, and N. Hameed, “Sentiment Analysis using SVM: A Systematic Literature Review,” Int. J. Adv. Comput. Sci. Appl., vol. 9, no. 2, 2018.
- A. Iqbal and S. Aftab, “A Feed-Forward and Pattern Recognition ANN Model for Network Intrusion Detection,” Int. J. Comput. Netw. Inf. Secur., vol. 11, no. 4, pp. 19–25, 2019.
- A. Iqbal, S. Aftab, I. Ullah, M. A. Saeed, and A. Husen, “A Classification Framework to Detect DoS Attacks,” Int. J. Comput. Netw. Inf. Secur., vol. 11, no. 9, pp. 40-47, 2019.
- S. Behal, K. Kumar, and M. Sachdeva, “D-FAC: A novel ϕ-Divergence based distributed DDoS defense system,” J. King Saud Univ. - Comput. Inf. Sci., 2018.
- S. Aftab, M. Ahmad, N. Hameed, M. S. Bashir, I. Ali, and Z. Nawaz, “Rainfall Prediction in Lahore City using Data Mining Techniques,” Int. J. Adv. Comput. Sci. Appl., vol. 9, no. 4, 2018.
- S. Aftab, M. Ahmad, N. Hameed, M. S. Bashir, I. Ali, and Z. Nawaz, “Rainfall Prediction using Data Mining Techniques: A Systematic Literature Review,” Int. J. Adv. Comput. Sci. Appl., vol. 9, no. 5, 2018.
- S. Wang and X. Yao, “Using class imbalance learning for software defect prediction,” IEEE Transactions on Reliability, vol. 62, no. 2, pp. 434–443, 2013.
- J. C. Riquelme, R. Ruiz, D. Rodr´ıguez, and J. Moreno, “Finding defective modules from highly unbalanced datasets,” Actas de los Talleres de las Jornadas de Ingenier´ıa del Software y Bases de Datos, vol. 2, no. 1, pp. 67–74, 2008
- F. Lanubile, A. Lonigro, and G. Visaggio, “Comparing Models for Identifying Fault-Prone Software Components,” Proc. Seventh Int’l Conf. Software Eng. and Knowledge Eng., pp. 312–319, June 1995.
- K. O. Elish and M. O. Elish, “Predicting defect-prone software modules using support vector machines,” J. Syst. Softw., vol. 81, no. 5, pp. 649–660, 2008.
- I. Gondra, “Applying machine learning to software fault-proneness prediction,” J. Syst. Softw., vol. 81, no. 2, pp. 186–195, 2008.
- O. F. Arar and K. Ayan, “Software defect prediction using cost-sensitive ¨ neural network,” Applied Soft Computing, vol. 33, pp. 263–277, 2015.
- C. Manjula and L. Florence, “Deep neural network based hybrid approach for software defect prediction using software metrics,” Cluster Comput., pp. 1–17, 2018.
- R. Moser, W. Pedrycz, and G. Succi, “A Comparative Analysis of the Efficiency of Change Metrics and Static Code Attributes for Defect Prediction”, In Robby, editor, ICSE, pp. 181–190. ACM, 2008.
- E. Giger, M. D’Ambros, M. Pinzger, and H. C. Gall, “Method-level bug prediction,” in ESEM ’12, pp. 171–180, 2012.
- S. E. S. Taba, F. Khomh, Y. Zou, A. E. Hassan, and M. Nagappan, “Predicting bugs using antipatterns,” in Proc. of the 29th Int’l Conference on Software Maintenance, pp. 270–279, 2013.
- K. Herzig, S. Just, A. Rau, and A. Zeller, “Predicting defects using change genealogies,” in Software Reliability Engineering (ISSRE), 2013 IEEE 24th International Symposium on, pp. 118–127, 2013.


