A Genetic Approach Based Solution for Seat Allocation during Counseling for Engineering Courses

Published Online January 2016 in MECS

Student Counseling is a recurring activity being carried out in almost all universities and educational institutes globally. In India there are thousands of colleges and millions of students seeking admission in these colleges. The process of allocation of college to a particular student is based upon a common admission test conducted by some central coordinating institute. The students has been awarded with a rank based upon the marks scored by them in common admission test also student fills their own choices for colleges. Now onwards the real process of seat allocation starts and it’s a complex task. Because sometimes a good rank holder student may apply for a low rank college because of his suitability (nearer to his home etc.) and makes the process cumbersome.

This process aims at allocating the students the courses in the institute as per their choice and area of interest. As experienced, this is a bulky process as it involves a number of comparisons, permutations and combinations among the various available institutes and courses (branches of a particular course) in a centralized manner. For instance, if we take up the case of our own Himachal Pradesh University (a provincial university in India), there are about 25 affiliated colleges running the Bachelor of Technology course with a total of about 8 different branches like CSE, IT, EE etc. All the colleges are not offering all these 8 branches.

It is a tough task to allot all the prospective students a seat in particular branch of a particular engineering college of their choice and that too based on the ranks scored by them in a common entrance examination. This workload has been one of the most difficult tasks faced by the centralized management. A good scheduling technique leads for the optimization of the entire process. Our problem involves distribution of seats among branches, colleges to different ranks. We have to allocate a seat to a particular rank holding candidate based on the marks obtained in the entrance examination and the choice of the candidate. This would be feasible if and only if certain constraints are satisfied. These constraints are typically divided into hard and soft constraints.

Because of its characteristics and variety of constraints, such a problem can be considered to be a Non-deterministic Polynomial-time (NP) hard problem [1]. This has led to an increased emphasis on finding effective automated algorithms for solving such problems. Genetic algorithm based approach is one of the thrust areas in this direction to solve such problems. In this work, we propose a powerful genetic algorithm as a solution to the seat allocation problem in colleges under the centralized management of a single affiliating University.

Hard constraints must not be violated (in our seat allocation problem, a hard constraint might be that no student is scheduled to acquire two seats in the table).There is also a list of second order constraints (or soft) constraints which should be taken into account. Soft constraints possess a penalty for being violated.

• II.    Problem Statement

Currently, seat allocation scheduling is carried out manually and is a time consuming process. This process uses the clustering and heuristic method. The seats to the students are allocated based upon their choices and availability. There are redundancies and re-scheduling process is even more complicated. Our genetic algorithm based solution tends to minimize the manual efforts and the time required by automating the counseling process such that the algorithm itself advocates for the best possible allocation of seats to all the students based upon their preferences. All the constraints like non availability of seats etc. are also handled automatically by the computer program. Overall, our solution assists the management as well as the students in the decision making process.

• III.    Research Objective

The objectives of our study are as follows:

• •    To optimize the seat allocation problem process.

• •    To purpose a new Genetic algorithm for the seat allocation problem for this optimization.

• IV. Related Work

The seat allocation can be considered as a scheduling problem [2]. The constructions of seat allocation table (SAT) is very complex where a lot of constraints should be followed. However, there are several techniques that have been used to find the optimized solution to the seat allocation problem such as Tabu search, Ant algorithm, Simulated Annealing and others. But the study of corresponding literature suggests that genetic algorithm are better than all the above discussed techniques[3][4]. The main objective is to find schedules to satisfy a numbers of hard and soft constraints.

Some studies have employed different kinds of scheduling applications [2] as represented in Fig 1. techniques in scheduling using GA.

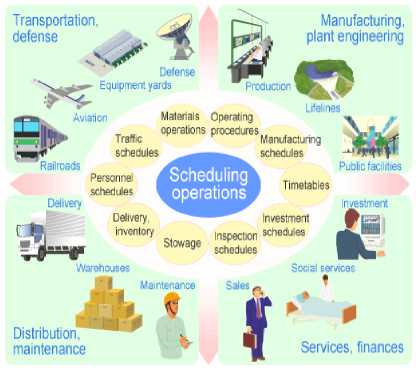
Fig.1. Diverse Scheduling Problems [2].

Our problem at hand, involves scheduling a number of seats to branches and colleges to a fixed set of ranks scored on the basis of marks obtained in the entrance examination and also we have to consider the priorities filled in by the candidates during the application procedure. Next, we discuss about GA in Seat Allocation problem, which is a special version of the optimization problems in which there are classified hard and soft constraints to be satisfied by the Seat Allocation Table (SAT).

Basically, in the case of SAT, the fitness function for a chromosome representing a Seat Allocation table involves various problems such as clashes, allocation of seats based on the priorities set by the students etc. It then performs mutation and produce Seat Allocation tables whose fitness values are evaluated and a table with no clashes can be finalized.

Filho and Lovena in [5] present the improvement applications in GA’s for examination timetabling problem. The genetic algorithm has been enhanced with local optimization techniques which are based on problem. Specific heuristics have also been incorporated into the genetic operators. In this problem, there are hard and soft constraints to be satisfied [5].

D. Stefano & A.Tettamanzi [6] propose the powerful techniques in scheduling using GA. School timetabling problem is one of the applications in scheduling. In one aspect, it deals with class and Teachers such that it fulfills the proposed time slots. These aspects are important for the School timetabling so as to carry the process smoothly. One of the constraints is that no teacher be allocated can sit more than one subject in the same timeslot. The other constraint is that for any teacher, the workload should be arranged to have less than three subjects in a row [6].

Melicio et al. find out the three main categories [7] of timetabling problem:

• •    Class/Teacher timetabling:

The weekly scheduling of all classes, avoiding teachers meeting two classes in the same time slot and vice-versa.

• •    Course timetabling:

The weekly scheduling for all lessons of a set of courses, minimizing the overlaps of lessons of courses having common students.

• •    Examination timetabling:

The scheduling for the examination of a set of courses, avoiding overlapping examination of courses having common students and spreading the exams for the students as much as possible.

The author applied GA in this optimization problem because they considered it robust enough in such a huge problem space [7].

Gyori et al. discuss about GA [8] in timetabling problem and suggest that it is a special version of the optimization problems. They introduce a new representation, which meet the demands better than previous. Students, teachers, lessons and classrooms have to be arranged optimally. They list out various classified hard and soft constraints that are to be satisfied by the timetables. The method proved to be efficient in real life application of a secondary school. The representation meets the demands better than the former ones [8].

• V.    Basic Terminology

• A.    Non-deterministic polynomial-time hard problem (NP)

NP are those computational problems for which solutions can be verified by a non-deterministic Turing machine in polynomial time (or less), whereas, NP- hard are those problems which are at least as hard as the hardest problems in NP.

• B.    Scheduling

A process where we have to map a number of alternatives against a fixed number of slots is known as scheduling process [10].

• C.    Elitism

The best individual (or the ‘n’ best individuals, respectively) of the previous generation is/are retained for the next generation if it/they represent the best solutions[11].

• VI.    Genetic Algorithm

Genetic algorithm approach is a general purpose optimization tool based on the Darwin’s theory of evolution with the capability to produce optimized solutions even when the dimensions of the problem increase and for this reason they have been successfully applied to a wide variety of problems [8]. It is a search algorithm derived from the simple concept of “survival of the fittest” in Biology [9]. A genetic algorithm performs a directed search of a solution space in order to find an optimal solution for some problem. GA’s have been used for many different applications including scheduling, predicting the stock market, creating art etc. They operate on a population of possible solutions represented in mathematical terms. Each member of the population consists of a number of genes, each of which is a unit of information. New solutions are obtained by combining genes from different population members (crossover) to produce offspring or by altering existing members of the population (mutation).

GA represents data as chromosomes. Chromosomes are typically simple strings of data and instructions often given as individual genes. The basic GA is as below:-

• 1.    Initialization- Generate random population of ‘n’ chromosomes (suitable solutions for the problem).

• 2.    Fitness-Evaluate the fitness function f(x) for each chromosome ‘x’ in population.

• 3.    New population-Create a new population by repeating the following steps until the new population is complete:

• a)    Selection-Select two parent chromosomes from the population according to their fitness (better the fitness, bigger are the chances to be selected).

• b)    Crossover- With a crossover probability crosses over the parents to form a new offspring. If no crossover was performed, offspring is the exact copy of parents [12] [13].

• c)    Mutation-With a mutation probability mutate new offspring at each locus (position in chromosome).

• d)    Accepting-Place new offspring in the new population.

• 4.    Replace-Use new generated population for a further run of algorithm.

• 5.    Test-If the end condition is satisfied, stop, and return the best solution in current population.

• 6.    Loop: Go to step 2.

Fig.2 explains the framework for a general problem using Genetic Algorithm. It is a general method for problem solving using evolution strategies and evolutionary programming.

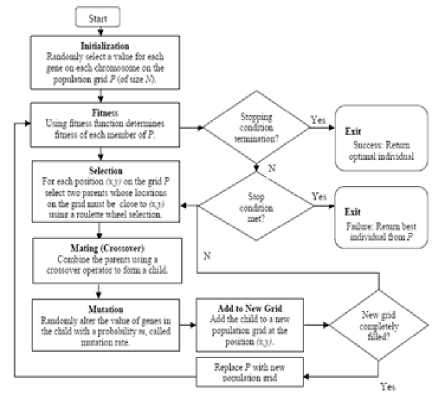
Fig.2. Flowchart Representation of Genetic Algorithm [3].

• VII.    Proposed Algorithm

• A.    Description of the problem

The problem aims at allocating students the courses in the institute as per their choice and rank scored in the entrance examination. This would be feasible if and only if certain constraints are satisfied.

• B.    Problem Representation

Our seat allocation problem consists of a set of Rank holding students in the combined merit list, R = {r 1 , r 2 ,…., |r|}, a set of branches B = {b 1, b 2 ,..., |b|}, a set of colleges, C = {c 1 , c 2 ,…., |c|} and a set of category codes Z = {z 1, z 2 ,..., |z|}. The goal is to obtain an allotment where each seat based on rank r ϵR is allocated to an available slot in a seat allocation table. The seat allocation problem involves scheduling for the seats, branches, colleges and ranks. We have to allot a seat to a particular rank based on the marks obtained in the entrance examination. Each branch may have a maximum of 60 seats (an assumption). Each college has different branches (e.g. b1, b2, b3, b4, b5……). We denoted by S the set of all the seats. For each seat sϵS the maximum no. of seats must be given as part of the input. C is the set of colleges available in a university. Some colleges can have only few branches. R denotes the set of ranks based on the marks scored in entrance examination. A seat allocation table is feasible if and only if the certain constraints are satisfied. These constraints can be divided into hard constraints, which must not be violated (in the class timetabling Problem, a hard constraint might be that no teacher is scheduled to teach two subject at once).

In a simple GA, chromosomes are represented as bit strings. We believe that problem specific knowledge should be incorporated in the representation of solution to our seat allocation problem.     Chromosome representation should contain all the relevant information and be close to the original problem. In this sense, it is straight forward to define a seat allocation table to be a map

f: R x Z x C x B ^ {0,1}

Where f(r, z,c,b) =1 if and only if seat s is allocated to rank r in a college c with branch b and category code z..

Such a mapping is easily translated into facts of the form:

Rank

Cat. code

College preference

Branch preference

Weight College

Weight Branch

Fig.3. Data to be Filled by Student

Set of Constraints:-

The set of Constraints in our problem can be stated as follows:

• 1.    All colleges do not support all the available branches. Some colleges may have only a few branches.

• 2.    A branch in a college may have at the most 60 seats (assumption).

• 3.    A student should not be allocated multiple seats.

• 4.    Candidates are suggested a seat based on to the preference and availability

• 5.    A candidate should not be allocated a non-existing branch in a college.

• 6.    The seat allocation shall be on the basis of a combined merit list.

• 7.  The same procedure is to be followed for the

• 8.  The students are suggested seats as per their

candidates in the waiting list.

preference and the weights (which they assign in favour of particular college and branch).

Here, 2, 3, 6 are hard constraints. 1, 4, 5, 7, 8 are specification constraints.

• C.    Initialization

The initialization procedure creates a population of feasible solutions at random. Our objective, valid for the whole algorithm, is to start with. Otherwise, in a highly constrained problem like ours, “one runs the risk of creating a genetic algorithm legal seat-allocation-tables and never leave this search space that spends most of its time evaluating illegal individuals” [8], and the chances of an effective search for good solutions would be very low.

The price we have to pay for this is that initializing a population (and defining advanced genetic operators) is not a simple task. In fact, the problem is known to be NP-hard [1]. Nevertheless, our assignment procedure succeeds in producing an initial population. The members of this population, however, suffer from very poor fitness, in general i.e. they may contain a large number of ‘holes’ e.g. branches are allocated to lower ranked candidates, even though this might not be possible in practice.

A number of necessary conditions (hard constraints) for the existence of solutions are checked before we start the initialization process. seats are selected in random order, and each seat is assigned to a randomly chosen rank without violating any hard constraint. The colleges and branches are selected according to a list of priorities.

We initiate our solution by assigning the branch and college to the applicants with zero penalty based on their choices. It will generate a population with least penalty. However, it may also be the most unfit population leading to inconsistent results because the initialization routine does not care at all about soft constraints. Handling soft constraints is left to the evolutionary process that follows.

• D.    Evaluation

Our evaluation function is made up in the form fitness costf(x) = ∑ Ԝс․ Рс + ∑ Wb. Pb (1)

Where m= Population size (total no. of colleges) and n= Total no. of branches in a college.‘Wc’ is the weight assigned to college and ‘Pc’ is the value of penalty imposed for the college and ‘Wb’ is the weight assigned to branch and ‘Pb’ is the value of penalty imposed for the branch.

Here, P is the penalty value imposed to the violation of a specific soft constraint. P may count, for instance, the number of undesirable ‘holes’ in the SAT ‘f’. Note that we do not need to impose penalties on violated hard constraints because the concept of our domain-specific genetic operators is to produce only feasible solutions.

The values of the evaluation function range from 0100%, and our genetic algorithm aims at finding a Seat Allocation Table (SAT) which maximizes this function. We are experimenting with different settings {w 1 , w 2 ,…,w n } of weights for the components of the fitness function. Often it is hard to decide which soft constraints should be considered to be more important than others. Candidates, for instance, may mark higher priority for a college nearby to their home. The feasible table is penalized for each occurrence of the constraints. It generates the data, optimizing the table to avoid clashes and maximize the fitness f(x).

• E.    Mutation

Mutation is a genetic process used to maintain genetic diversity from one generation of a population of genetic algorithm chromosomes to the next [14][15]. It is analogous to biological mutation. Mutation alters one or more gene values in a chromosome from its initial state. In mutation, the solution may change entirely from the previous solution. Hence the GA can reach to better solution by using mutation. A very successful (slight) variant of the general process of constructing a new population is to allow some of the better organisms from the current generation to carry over to the next, unaltered. This strategy is known as elitist selection.

We carry forward chromosomes from the previous generations to the new one through the property of elitism if the following constraints are not violated:

• •    Assigned seat (branch, college combination) is already allocated to some other rank holder.

• •    Assigned branch is unavailable in the assigned college.

• •    The total number of seats in a particular branch of a college is already assigned.

• VIII.  Llustration

The concept presented in the previous section can be verified and validated through a hypothetical illustration as presented next:

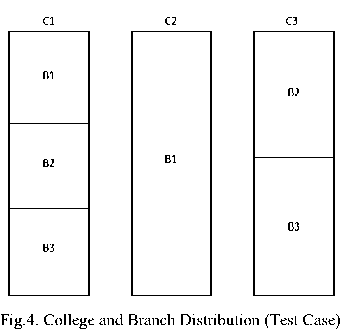
Suppose, there are 3 engineering colleges (represented as 1, 2, 3) under a university participating in the counseling process. There are a total of 3 branches (represented as 1, 2, 3) offered by the university. Each branch in a college can accommodate only a single student. The branch availability in colleges is as represented in fig.3. We have a total of 6 seats that are to be assigned among 10 students such that no seat is allocated twice and there are no conflicts as per the assumptions.

Assumptions:

• •    Set of colleges, C = {1,2,3}

• •    Set of branches, B ={1,2,3}

• •    Set of rank holders in the merit list,

R = {101, 102… 110}

• •    Weight assigned to college by a student, w c

• •    Weight assigned to branch by a student, w_b.

• •    Preference assigned to a college by a student, set X_c

• •    Preference assigned to a branch by a student, set X_b

• •    Total no. of seats in a branch = 1.

Student Data

R	Xc 3	Pc 0	Xb 1	Pb 0	Wc	Wb
101	2	1	2	1	8	2
	1	2	3	2
	1	0	3	0
102	2	1	1	1	6	4
	3	2	2	2
	1	0	3	0
103	3	1	1	1	4	6
	2	2	2	2
	2	0	1	0
104	1	1	2	1	7	3
	3	2	3	2
	1	0	1	0
105	3	1	3	1	3	7
	2	2	2	2
	2	0	3	0
106	1	1	1	1	1	9
	3	2	2	2
	3	0	1	0
107	1	1	2	1	9	1
	2	2	3	2
	1	0	1	0
108	2	1	3	1	6	4
	3	2	2	2
	1	0	1	0
109	3	1	3	1	3	7
	2	2	2	2
	1	0	3	0
110	2	1	1	1	6	4
	3	2	2	2

Fig.5. Student Data.

The data presented in Fig.5 has been assumed to have been entered by the students while filling up the counselling forms.

In the first generation, all students in Fig.6 are allocated the colleges and branches of their choice in the order of merit. The fitness cost in this case is 0, where as the overall generation fitness is 50%.

Rank	College	Branch	Success	Constraint	Penalty
101	3	1	N	Branch is not available	0
102	1	3	Y		0
103	1	3	N	Seat already allocated	0
104	2	1	y		0
105	1	1	y		0            Fitness Cost         0
106	2	3	N	Branch is not available	0       Generation Fitness %   50
107	NA	NA			NA
108	NA	NA			NA
109	NA	NA			NA
110	NA	NA			NA

Fig.6. First Generation after Mutation.

In the 2nd generation, the property of elitism holds good for the students, who have not been allocated any seat, and thus are assigned the next preferred college and branch as per the weights assigned by them. In this case as shown in Fig.7, fitness cost is 7 and overall generation fitness is 83%.

Rank	College	Branch	Success         Constraint	Penalty
101	3	2	y	2
102	1	3	Y	0
103	3	3	y	4
104	2	1	y	0
105	1	1	y	0	Fitness Cost         7
106	1	3	N      Seat already allocated	1	Generation Fitness %   83
107	NA	NA

108 NA     NA

109 NA     NA

110 NA     NA

Fig.7. Second Generation after Mutation.

In the 3rd generation, the property of elitism holds good again for the students who have not been allocated any seat and hence are assigned the next preferred college and branch as per the weights assigned by them. In this case as shown in Fig.8, fitness cost is 8 and overall generation fitness is 83%.

Rank College Branch Success Constraint Penalty

101     3        2       y2

102     1       3       Y0

103     3       3       y4

104     2        1       y0

105      1        1        y                                    0 Fitness Cost8

106     3       3 N Seat already allocated 2 Generation Fitness %83

107    NA     NA

108    NA     NA

109    NA     NA

110    NA     NA

Fig.8. Third Generation after Mutation.

In the 4th generation the property of elitism still holds good for the students who have not been allocated any seat and now are assigned the next preferred college and branch as per the weights assigned by them. In this case, fitness cost is 15 and overall generation fitness is 83% as shown in Fig. 9.

Rank	College	Branch	Success      Constraint	Penalty
101	3	2	y	2
102	1	3	Y	0
103	3	3	y	4
104	2	1	y	0
105	1	1	y	0            Fitness Cost        15
106	2	1	N      Seat already allocated	9       Generation Fitness %   83
107	NA	NA
108	NA	NA
109	NA	NA
110	NA	NA
		Fig.9. Fourth Generation after Mutation.

In the 5th generation the property of elitism still holds good for the students who have not been allocated any seat and so are assigned the next preferred college and branch as per the weights assigned by them. In this case, fitness cost is 16 and overall generation fitness is 83% as shown in Fig. 10.

Rank College Branch Success      Constraint      Penalty

101      3        2        y2

102     1       3       Y0

103     3       3       y4

104      2        1        y0

105      1        1        y                                    0 Fitness Cost16

106     1       1       N Seat already allocated 10 Generation Fitness %83

107    NA     NA

108 NA NA

109 NA NA

110 NA NA

Fig.10. Fifth Generation after Mutation.

In the 6th generation the property of elitism still holds good for the students who have not been allocated any seat and hence, are assigned the next preferred college and branch as per the weights assigned by them. As shown in Fig. 11, fitness cost is 17 and overall generation fitness is 83%.

Rank College Branch Success      Constraint      Penalty

101      3        2        y2

102     1       3       Y0

103     3       3       y4

104      2        1        y0

105      1        1        y                                    0 Fitness Cost17

106     3       1 N Branch is not available 11 Generation Fitness %83

107    NA     NA

108    NA     NA

109    NA     NA

110    NA     NA

Fig.11. Sixth Generation after mutation.

In the 7th generation the property of elitism again holds good for other students who have not been allocated any seat and hence, are assigned the next preferred college and branch as per the weights assigned by them. In this case, fitness cost is 24 and overall generation fitness is 83% as shown in Fig.12.

Rank College Branch Success
101	3	2	y
102	1	3	Y

103	3	3	y
104	2	1	y
105	1	1	y
106	2	2	N
107	NA	NA
108	NA	NA
109	NA	NA
110	NA	NA

Constraint       Penalty

Branch is not available 18

Fitness Cost

Generation Fitness %

Fig.12. Seventh Generation after Mutation.

In the 8th generation the property of elitism holds good again for other students who have not been allocated any seat and so are assigned the next preferred college and branch as per the weights assigned by them. In this case, fitness cost is 25 and overall generation fitness is 100% as shown in Fig. 13.

Rank	College	Branch Success	Constraint	Penalty
101	3	2y		2
102	1	3Y		0
103	3	3y		4
104	2	1y		0
105	1	1y		0            Fitness Cost        25
106	1	2Y		19      Generation Fitness %   100
107	NA	NA
108	NA	NA
109	NA	NA
110	NA	NA
		Fig.13. Eighth Generation after Mutation.

In the final generation i.e. eight generation the fitness value reaches up to the maximum i.e. 100% for the example we taken under consideration. That should be our prime aim to increase the fitness value of a function up to maximum.

• IX. Conclusion

We observe here that the seats being assigned to the students through our procedure follow a sequential pattern in successive generations. The plot for generation versus fitness as shown in Fig.14.

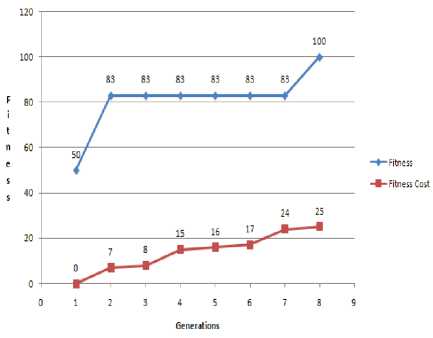
Fig.14.Fitness v/s Generation to each other. They are increasing in successive generations. With an increase in generation fitness, we observe an increase in the penalty value, thereby increasing the fitness cost. Although in some generations the value of fitness remains constant but the overall value of fitness is increasing.

In order to increase the overall generation fitness, we have to pay a higher penalty and high fitness cost.