A Geodesic Active Contour Level Set Method for Image Segmentation

Published Online June 2012 in MECS

Segmentation process is normally defined as identifying and imagining the restrictions of the objects enclosed in a given image. To partition the image in an efficient manner, the well-known tool is the active contour model (also called snake model, or deformable model). For example, in high throughput image, sit is necessary to store a large number of images to extract the information. Therefore, it is vital to fragment each image into significant partitions in an exact, rapid, automated and robust way. The crisis of image segmentation is basic to image processing.

For image segmentation, many advanced approaches were developed. Some of them are clustering, histogram-based, region-growing, graph partitioning and optimization model-based. From these advanced segmentation approaches, optimization model-based methods frequently provide very potential results, offered that the primary optimization problem is resolved precisely. A benefit of this approach is that one can include domain knowledge into the model clearly through exact mathematical modeling.

To enclose the detected object, contour is used and its deformable models intends at making this contour change so that it matches the edge of the considered object. The contour has taken the object for the entire which is related to an energy-minimization problem. The energy functional is defined as a weighted mixture of both internal forces (relating properties of elasticity and rigidity of the contour) and external forces (that show the curve towards the boundary of the object).

The Geodesic active contour (GAC) approach is based on the relation between active contours and the computation of geodesics or minimal distance curves. The main properties of GAC are 1) Illustrates the relation between energy and curve progress approaches of active contours. 2) Presents dynamic curve for object detection as a GAC approach. 3) Expand existing curve progression models as a result of the GAC formulation. 4) Permit concurrent recognition of interior and exterior boundaries in numerous objects without unique contour tracking procedures. 5) Holds proper existence, individuality, firmness, and reliability results. 6) Does not need particular stopping conditions.

The topological flexibility is a great benefit since it permits the concurrent discovery of numerous objects in the image, which was impossible in the case of parametric deformable models. In brain imaging, for example, when situated near a lobe, parts of the shape may wrinkle and at last have a contact point (without merging), which is not reliable with the round topology of the brain. The comparison of the image can also be spoiled and the number of components of the object can thus be improved.

• II.    LITERATURE REVIEW

  [Yan Nei Law, Hwee Kuan Lee et. Al, 2008] presented a technique for image segmentation using a Multiresolution Stochastic Level Set Method for Mumford–Shah [S. Esedoglu and Y. H. Tsai, 2006] Image Segmentation. One of the most successful image segmentation models is Mumford–Shah model.

Though gradient descent based methods are well-known to discover a limited minimum only, still numerous stochastic methods do not offer a realistic solution to this problem either.

[Carole Le Guyader and Luminita A. Vese, 2008] proposed a technique as Self-Repelling Snakes for Topology-Preserving Segmentation Models. Nevertheless, in some applications, this topological flexibility is adverse or the resulting shape must be homeomorphic to the initial one. The requirement of designing topology-preserving processes happens in medical imaging. [Mohamed Ben salah et. Al., 2011] developed a Multi region image segmentation using parametric kernel graph cuts. [H. K. Lee and Y. Okabe, 2005] used nonequilibrium Markov processes with nonequilibrium Markov processes for an image segmentation. [A.-P. G. Haramis, A. Hurlstone et. Al., 2006] presented an Adenomatous polyposis coli-deficient which are susceptible to digestive tract.

[G. Sundaramoorthi and A. Yezzi, 2007] developed a technique as Global regularizing flows for topology preservation in active contours [M. Rochery, et. Al., 2006] and polygons with dual geometric active contour [G. Zhu, et. Al., 2006]. For a sequential sampling methods, [H. K. Lee, Y. Okabe et. Al.,, 2006] produced convergence and refinement of the image segmentation technique. To integrate the color, texture, motion of the image [ D. Cremers, M. Rousson et. Al.,, 2007] presented a statistical approach for level set segmentation process. [G. Zhu, Q. Zeng et. Al.,, 2006] identified a new technique as dual geodesic image segmentation process using active contour images. After segmentation, if noise occurs, [T. F. Chan, S. Esedoglu et. Al., 2006] used algorithms for finding global minimizes of denoising and segmentation models. If segmentation is done, there is a chance of topology changes. The topology of the network should be preserved [Carole Le Guyader et. Al., 2008].

Finally, in this work we are going to present image segmentation using GAC level set methods. The experiments are carried over to prove the proposed GAC level set methods is better than an existing Multi resolution Stochastic Level set method (MSLSM) for Image segmentation.

• III.    GAC LEVEL SET METHOD FOR IMAGE

SEGMENTATION

The proposed image segmentation using geodesic active contour with level set method is efficiently designed for making the image segmentation process more clear. For image segmentation, active contours have turn out to be very popular for applications in image processing. Based on the illustration of active contours, they can be normally divided into two categories, the explicit active contours presented by point sets or B-splines and the implicit active contours presented by level set functions. The given medical image segmentation is done through the proposed GAC level set method ton identify the affected area of the image and processed the given set functions. The proposed image segmentation using geodesic active contour with level set method is explained briefly below with architecture diagram Fig 3.1.

• A.    Geodesic Active Contour

Let I ( x , y ) : Q ^ R ± be a given gray-scale image. The geodesic active contour as an evolving curve is denoted by C(t) and represented by the zero level set of a level set function ф ( t , x , y ) , i.e.,

C(t)^{(x, y )ф(t, x, y )^ 0} . The level set function ɸ is normally selected to be a signed distance function that is negative in the interior and positive in the exterior of the zero level set. The evolution of the geodesic active contour embedded in the level set function can be formulated by the following partial differential equation:

d ^ = g ( I )| |VO|| [ dz"v | VФVФ■ v ) ] +V g ( I ) xVO ^{( 1} )

Where v is a constant parameter controlling the balloon force, and g is the edge indicator function, which is commonly defined by

g ⁽ I ) =-------- ¹------- 2                (2)

1    + V(Gct x I) ||

Where Gσ denotes the Gaussian filter with standard deviation σ. With an appropriate initialization, the evolving curve C represented by the zero level set of the level set function ɸ will stop at the desired edges where the function g is approximated to zero. The GAC for image segmentation is referred in [14].

Through geodesic active contours, it analyzed the given image clearly for image segmentation. After analyzing the given image, the level set method is applied to the form a active cluster object. Cluster object formation is done with fuzzification of growing active contours with the previously known contours of diseased image portion of the given medical image portion.

Figure 1. Architecture for image segmentation using GAC level set methods

To address the issue of topology preservation in segmentation problem, we have proposed a geodesic active- contour based model that combines a topological restriction across worldwide. This topological restriction is based on a geometrical observation and can be seen as a resisting force in the progression problem. The proposed image segmentation using geodesic active contour with level set method efficiently preserved the topology specifications, when image has been segmented. If topology of the image changes, the level set method is applied to obtain the better quality. If the topology of the image remains the same, then the active cluster objects of the image are segregated to obtain the image clarity.

• B.    Level set based GAC Algorithm

The GAC method obtains an initial solution to its respective local minimum. This method is used to optimize FMS (ɸ , C) with respect to ɸ . Starting from a given initial guess ɸ0, we update ɸ and C alternatively. The following steps have to be followed to perform the level set based GAC:

• 1    Given Input: let C(q): [0,1]->R² be a planar curve

• 2    Let I: [0,a] * [0,b] -> R+ be a given image

• 3    Output: Detect the object boundaries

• 4    Compute the association of curve C with energy

E(C) = aj| C 1()(q)2dq + вj| C11 (q^dq-jvI(C()q)dq(3)

• 5    Apply the level set GAC method starting from a ɸ⁰ , 6 Compute C ^k, for the given fixed ɸ ^k-1,

C k = min c FMS (ɸ k-1, C)(4)

• 7    Repeat the process until get the original image resolution

• 8    Increase the image resolution in a factor of 2

• 9    Use the level set function of GAC, Refer eqn (1)

• 10    Set the current segment C (curr)

• 11    For the topology constrained problem in GAC level set method,

• 12    Assume ɸ that is a signed-distance function to C

• 13    ɸ(x) = dist (x,C)                               (5)

• 14    If topology changes, decrement the value of ɸ(x)

• 15    else use Euclidean scalar product (refer.[11])

• 16    End If

• 17    Ends

The above algorithm steps have to be followed for the image segmentation using GAC level set methods.

• IV.    PERFORMANCE EVALUATION

Experiments for different kinds of images were presented. These experiments express the capability to notice several objects, as well as the capability to notice interior and exterior boundaries at the same time. The experiment is taken over with given medical image shown in fig 1 which is taken as input image. The performance of the image segmentation using GAC level set methods is tested under medical images. It is necessary to get the clear and quality image when it is segmented into equal meaningful partitions. The segment size defines the size of the partitioned image in a meaningful format. Even after partition is done with the image, how the clarity of the image would be. The contour growth defines the sharpness level of the image after it gets partitioned using GAC level set methods. The performance evaluation of the image segmentation process using GAC level set methods is done with

• i)    Segment size, ii) Contour growth iii) Performance rate

• V.    RESULTS AND DISCUSSION

When compared to an existing a Multi resolution Stochastic Level set method (MSLSM) for Image segmentation, the proposed GAC level set method for image segmentation performed better in terms of segment size and contour growth. The sharpness level of the image after segmentation is high in the proposed GAC level set method for image segmentation. The proposed image segmentation using geodesic active contour with level set method is tested with a sample set of given input image figure 2.

Figure 2. Input medical bladder image

After receiving the input image, Geodesic Active Contour is being applied to obtain an image with segmentation. The segmented image received by applying the GAC is shown in figure 3.

Figure 3. Segmented bladder image

Figure 4. Contour bladder image

After the segmentation of the image is done, the proposed level set based GAC is applied to the segmented image to get the clear image. The level set based GAC will produce the contour objects of the segmented image and found the object boundaries. Apply the level set function for each contour of the image to obtaining the image segmentation process in an efficient manner. The output image is shown in figure 5.

Figure 5. output image

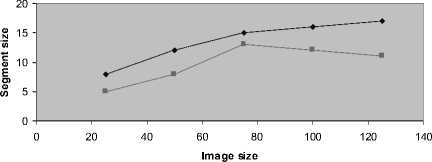
♦ Proposed GAC level set method —■— Existing MSLSM

Figure 6. Image Size vs. Segment Size

Above Figure describes the segmentation process of different image sizes. The performance graph of the proposed image segmentation using geodesic active contour with level set method based on segmented image sizes is shown in figure 6. When the image size increases, the segmentation process of that image is also be high to obtain a clear image quality. Since the proposed image segmentation using geodesic active contour with level set method used GAC level set method, the segmented image size will be somewhat larger than the existing MSLSM method. The proposed GAC level set methods provide a clear segmentation process rather than MSLSM for image segmentation.

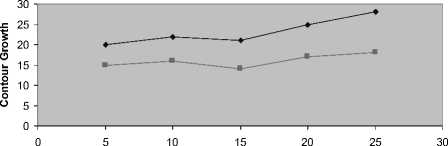
Image Segments

—♦— Proposed GAC level set method —■— Existing MSLSM

Figure 7. Image Segments vs. Contour Growth

Figure 7. describes the contour growth of different image segments. When the image segments increases, the sharpness level of that image is also be high to obtain a clear image quality. The performance graph of the proposed image segmentation using geodesic active contour with level set method based on segmented image sizes is shown in fig 5.2. When the image segments size increases, the contour growth of that image is also be high to obtain a clear image quality.

The proposed GAC level set methods provide a clear contour growth process rather than MSLSM for image segmentation.

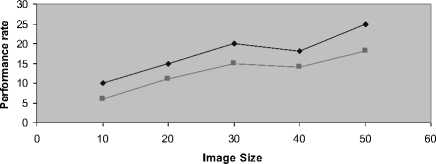
—♦— Proposed GAC level set method —■— Existing MSLSM

Figure 8. Image Size vs. performance rate

Figure 8. describes the performance rate of proposed GAC level set methods. When the image size increases, the performance rate of image segmentation process is high to obtain a clear image quality. The proposed GAC level set methods provide a clear image than MSLSM for image segmentation. Compared to an existing MSLSM method, the proposed GAC level set method is good in image segmentation process.

From this work, it is known that the proposed image segmentation using geodesic active contour with level set method efficiently done the image segmentation even the topology of the image changes often. The experimental evaluation is done with an existing MSLSM approach and showed the proposed image segmentation using geodesic active contour with level set method outperforms well.

• VI.    CONCLUSION

The proposed GAC level set methods briefly explained the segmentation process. The segmentation is made with GAC level set methods efficiently and the images were partitioned in a meaningful manner. After segmentation process, the image clarity is high using GAC level set method. The sharpness level of the image is being high. The GAC level set method initiated a novel term to the curve growth models that further magnetize the deforming curve to the boundary, by improving the detection of boundaries with large differences in their gradient. This term also partly frees the model from the need to estimate decisive parameters. When compared to an existing MSLSM for image segmentation, the proposed GAC level set method performed better in terms of segment size, contour growth and performance rate. The experiments were made with medical images. Finally, it proved that rather than using MSLSM for image segmentation, the proposed MSLSM is good for image segmentation process.