A Hybrid Approach for Image Segmentation Using Fuzzy Clustering and Level Set Method

The underlying objective of image segmentation is to partition an image into meaningful components of interest within the context of an application. The segmentation is normally based on some characteristics composed in an image such as grey level, color, pattern, texture, depth or motion, etc. There are several image segmentation techniques and their details can be found in [1, 2, 3]. However, the most widely used image segmentation technique is active contour model proposed by Caselles [4] as it is effectiely applicable for a broad category of image segmenation and image vision problems. Active contour models (ACM) can be divided into two main categories, namely, edge based active contour models and region based active contour models. The edge based active contour model uses image gradients to detect the boundaries of the objects to be segmented. On the other hand, region based ACMs utilize the statistical information contained in an image to control the evolution of contour in order to detect the exterior and interior boundaries of the object constituents simultaneously in an image.

Level set method [5] is an excellent tool for tracking boundaries and it has been successfully applied in image segmentation and visual tracking for a large class of applications in various fields like medical imaging, military, etc. However, traditional level set methods fail to achieve desired segmentation when an image contains several blocks with gradual variations in pixel intensities.

One of the most famous clustering algorithm, fuzzy c-means (FCM) algorithm [6, 7], is an unsupervised technique which has been successfully implemented in many fields like clustering, segmentation, etc. However, there are some deficiencies in traditional FCM algorithm. Therefore, several modifications have proposed to improve the performance of FCM algorithm [8, 9, 10, 11, 12].

It is obvious from the above discussion that neither level set method nor FCM algorithm alone can be relied upon to obtain a perfect result. Therefore, in this article, we are proposing a hybrid model that integrates modified fuzzy clustering with level set method based sign force function. In this hybrid model, first, we apply modified FCM on the given image and then result obtained thus serves as initial contour of the image for level set method to obtain more accurate segmentation of the image.

The remaining of the paper is organized as follows: Section II of the paper describes fuzzy c-means clustering algorithm for image segmentation. This also discusses level set method in general and its modification using signed pressure force function in particular. A new approach for image segmentation based on fuzzy c-means and level set method has been proposed in section III. In section IV, outcomes of the MATLAB implementation of the proposed image segmentation method have been presented. In section V, conclusions and future scopes of the paper have been discussed.

• II.    BACKGROUND

• A. Fuzzy clustering and spatial FCM

FCM clustering is an unsupervised technique initially proposed by Bezdek [7]. The main objective behind the proposal of this technique was to develop an FCM algorithm for distributing the clusters in such a way that obtained group of clusters minimizes the dissimilar elements in each cluster. It has been widely used in various applications of image processing such image segmentation, image enhancement, etc. [2, 3]. The FCM algorithm classifies pixels of an image data set into clusters based on Euclidean distance of a pixel from the center of the least distant cluster. For a given image data set X = ( x1, x2, x3, .., xn) with n pixels, to be partitioned into c clusters based on pixels characteristics, the FCM cost function [13, 14, 15] is defined as follow:

nc        ²

J =ZZ « m h- ч| ,                (1)

= 1 i = 1

where u ij represents the membership of an image pixel x j in the i th cluster, v i is the i th cluster center. || . || is a norm metric, and m is a constant that usually equals to 2 and controls the fuzziness of the partitioned clusters. The value of cost function J is minimum, i.e. membership values are high when image pixels are close to the centroid of their clusters. Similarly, the value of function J is maximum, i.e. membership values are low when image pixels are far from the centroid of their clusters. The membership function provides the probability of belonging of a pixel to a specific cluster. The membership value of a pixel is dependent on the distance between the pixel and centroid of its cluster. Equation (2) and equation (3) provide the updated values for membership function and cluster centers.

у JIXj - vil aSH) 6(1Xj- -Jr

n

Z « m x,

Vi = -=1------- in

E. m uij j=1

Each cluster center is guessed initially to start the algorithm, and then U and V are updated through iterations. When there is no change in either membership function or the cluster centers at two successive iterations, the procedure stops. Implementation of the FCM can be done using following steps [21].

Step 1: Initialize the membership matrix U according to the constraints.

Step 2: Find the cluster centers using equation (3).

Step 3:  (a) Check whether there is dissimilarity in calculated clusters according to equation (1). (b) Stop when there is no change in either membership function or the cluster centers at two successive iterations.

Step 4: If there is change occurred in any of the cluster then go to Step 2.

By applying the above steps, FCM method groups elements of the clusters to suitable cluster so that the distance between the element and its corresponding cluster center is minimum .

Suppose we are given four image elements, each of which has two image features, f1 and f2. Also, assume that FCM algorithm will partition these image elements into two clusters as shown in Table I.

TABLE I. IMAGE ELEMENTS AND THEIR FEATURES

Image Elements (I)	f1	f2
I 1	7	12
I 2	2	9
I 3	15	8
I 4	10	4

Figure 1 shows the pictorial representations of the image elements and their centroid positions on X-Y plane.

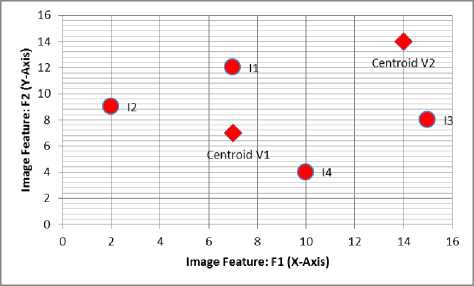
Figure 1. Illustration for centroids and image elements

In this example, c = 2 and let us assume that fuzziness control constant m = 2.

We also assume that the centroid of the first cluster, v1 = (7, 7) and second cluster, v2 = (14, 14).

Here, we can also assume that the image elements can be represented by using their image feature values as coordinate’s values, as shown in Table II.

TABLE II. ELEMENTS AND CORDINATE VALUES

Image Elements (I)	Coordinates values (f1,f2)
I 1	(7, 12)
I 2	(2, 9)
I 3	(15, 8)
I 4	(10, 4)

Initial membership functions for these clusters can be calculated using equation (2) as demonstrated below for the example given above in Table I and II.

у JI x j   v jl x( » -1)

Z

The calculations are as follows:

||X1 - ч||2 = [(7 - 7) 2 + (12 - 7) 2 ] =25

||x - v ||² = [(7 - 14)² + (12 - 14)²] = 49 + 4 = 51

Z( biZld)(2-1)   IIxi -vif + IIxi

^- =ⁱ  ll x i ^{- v}- ll             ||x i ^{- v} i||²    || x i ^{- v} 2||²

U11  2525

= 0.6710

" 2i

x i ^- v 2

IIxi - vilf u 2i = 5T51 = 0.3289

25 ⁺ 5i

Similarly, other values for membership function u can be computed and are given below.

u  = 0.8536 ; u  = 0.1464;

u  = 0.3627 ; u  = 0.6372;

u  = 0.8657 ; u  = 0.1343;

The membership relation corresponding to both clusters can be defined using following Table:

After finding membership values for image elements, FCM updates the centroid of the both clusters according to equation (3).

The centroid of first cluster v 1 can be computed as follows:

Z u.,x, v,= ji----

Z "i j=i

Substituting the values from Table III in the above equation we get,

_ (0.67i0) 2 (7,i2) +( 0.8536) 2 (2,9) +( 0^27) 2( i5,8) +( 0.8657) 2 (i0,4)

^{V i} =            (0.67i0)² + (0.8536)² + (0.3627)² + (0.8657)²

(14.0751, 16.0094)

v, = (  -    -  -     ) = (6.8335,7.7726)

¹         2.0597

Similarly, centroid of second cluster, v2, can be computed as follow:

Z "  2 ² j X

V2 = "^----

Z "  2 ² j

= i

Substituting the values equation we get, from Table III in the above

(0-3289) 2 (7,12)+(0^64) 2 (2,9)+(0-6372) 2 (15,8)+(0-1343) 2 (10^

(0.3289)² + (0.i464)² + (0.6372)² + (0.i343)²

(7.0695, 4.8098)

V. = —    ,-    ) = (i2.7723,8.6897)

²       0.5535

Figure 3 illustrates how centroids v 1 and v 2 move towards the center of two clusters formed by image elements I₁, I₂, I₄ and image element I₃ respectively.

TABLE III.       ELEMENTS AND MEMBERSHIP VALUES

Image Elements (I)	Membership values for cluster 1( u 1 j )	Membership values for cluster 2( u 2 j )
I 1	0.6710	0.3289
I 2	0.8536	0.1464
I 3	0.3627	0.6372
I 4	0.8657	0.1343

It is clear from the Table III that the membership value of image elements I 1 , I 2 , I 4 are more in first cluster and hence these are away from the first cluster and they fit into second cluster. Similarly, it can be argued that element I 3 is more towards first cluster.

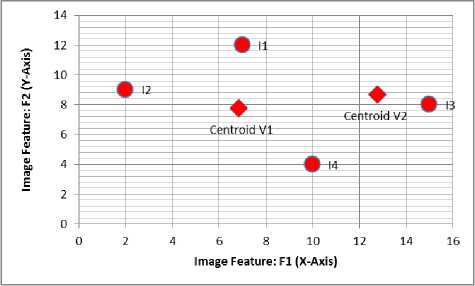
Figure 2. Illustration for centroids and image elements after first iteration of calculation for FCM

All the pixels of an image have high correlation with their neighboring pixels. It means if we create clusters based on image pixels features then there is a high probability of all these neighborhood pixels falling in same cluster. A spatial function [14] can be defined based on these neighborhood pixels features as

Applying chain rule,

Ф + Vф (x ( t ), t ). x ( t ) — 0,

N — E u*, k g NB ( xy)

where NB(x j ) represents a square window centered on pixel x j in the spatial domain. The spatial function h ij represents the probability that the pixel x j belongs to i th cluster. Now we can attach spatial function to membership function as in equation (5).

Since F is the speed of interface in the outward

'               V ф normal direction n, then F — n. x (t) , where n —

It gives the following interface evolution for ф .

ф, + F |V ф — 0,

'        ^ui^pj ^hi^qj

“ ,=            , ic    ,

E uh k=1

where F is the normal speed function.

For a general curve C, ф can be defined as a signed distance function to C

where p and q handles the relative importance of both functions u and h. In a homogenous region, the clustering results remain unchanged but, in case of regions consisting of noisy pixels, equation (5) reduces the weights of noisy clusters using the intensity level of its neighboring pixels to put it in correct cluster.

ф > 0,

ф ( x , y ) — \ф <  0,

ф — 0,

if ( x , y ) g insideC if ( x , y ) g outside C if ( x , y ) g C

B. Level set method with spf formulation

Level set method was proposed by Osher and Sethian [5]. It is a popular method for capturing moving boundaries or propagating interfaces. The core idea of implementing level set method is to begin with a closed curve or surface and move this curve perpendicular to itself at a specific speed.

To implement level set in image segmentation, we initialize a contour and then move it by using information lying in the given image. Let Ω be a bounded open subset of R² and I :[0, a ] x [0, b ] ^ R ⁺ be a given image. Let c ( q ):[0,1] ^ R ² be a parameterized planar curve in Ω. Zhang et al. [16] proposed the level set [19, 20] formulation using region based signed pressure force (spf) [18] function as follow:

ф — spf ( I ( x)) a |V ^ ,   x g Q .

Region (Outside)

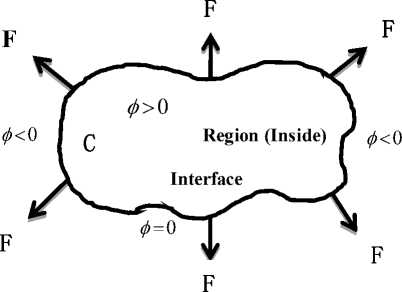
Figure 3. Curve C = {( x, y ): ф (X , y ) — 0 } propagating in normal direction [22]

where the spf( I(x) ) is given as follow:

I ( x ) -

spf ( I ( ^x ))^—---------- max( I ( x )

' 1 ^{+ c} 2

^“

C j + c₂

- , x g Q ,   (11)

)

where c 1 and c 2 are constants which are the average intensities inside and outside the contour respectively as defined by Chan and Vese [17].

The level set function ф in eq. (7) is defined as

'- P

ф ( x , t — 0) —<   0

Let the closed curve C in which its interface moves perpendicular to itself with a speed F. At any time, we can see from the Figure 3, the interface is given by the zero level set of time dependent level set function ф ( X , y , t ) — 0 . In order to find the movement of interface, we first require that the level set value of a particle on the front must always be zero [22], i.e.

ф ( X ( t ), t ) — 0

P

xgQ -dQ, x gSQ , xgQ-Q),

where p > 0 is a constant, Q is subset in the image domain Q and dQ is the boundary of Q .

III. PROPOSED ALGORITHM

Proposed hybrid approacch for image segmentation.

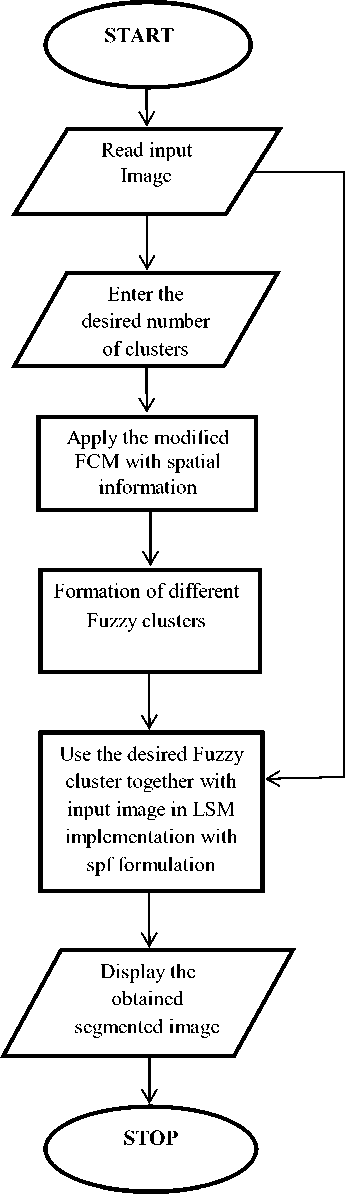
Figure 4. Proposed Hybrid Approach combining FCM and LSM with spf

FCM and level set methods can be used for image segmentation of a multidimensional image. Both of these methods can achieve good results in image segmentation. However, they fail to achieve desired segmentation in many images especially when the images have gradually varying scattered clusters contained in them. Therefore, in this section, we are proposing a hybrid approach combining fuzzy c-means and level set method implemented with signed pressure force function. The algorithm for implementing hybrid approach for combining FCM and level set methods is described as below:

Step 1: Read the input image.

Step 2: Define the number of clusters in which image pixels need to be divided.

Step 4: Use the desired Fuzzy cluster result obtained in step 3 to define initial contour for LSM.

Step 5: Use the contour obtained in step 4 together with input image in implementation of LSM with spf formulation defined in equation (10) to obtain final segmentation.

Step 6: Display the segmented image.

Figure 4 presents the steps described in the proposed algorithm.

• IV.     E xperiment simulation and result

ANALYSIS

The medical images pose real challenges to image segmentation techniques as these contains variations in illuminations, and sensor noise etc. The shadows, multiples variations etc come into existence when we capture the medical images. The proposed hybrid image segmentation algorithm described in section III was implemented using MATLAB. The MATLAB code was tested over several medical, mechanical, and other types of images. The displayed MRI medical image of knee has been taken from The results obtained here were very accurate and desired segmentation of image was obtained. Figure 5 contain an original image of MRI medical image of knee and its five Fuzzy clusters obtained using Fuzzy clustering with spatial FCM modification and Figure 6 show original and resulting segmented images.

• V.    C onclusion

Generally, the segmentation of medical images is not easy as proper segmented image can be obtained only by applying the series of suitable algorithms. The level set method used in this paper is a special form of Hamilton-Jacobi function. As the experimental results suggest, integrating fuzzy c-means and level set method with spf formulation can detect the segments of the image with a high degree of accuracy. The proposed model can be very useful to segment the image in medical and other fields. In future, we plan to use other modified versions of the level set methods along with modified fuzzy logic for improvement in image segmentation.

It should be noted that the algorithm suggested in this paper my not be suited for all types of medical images, especially for the images which taken in with low resolutions. For these types of images, there is big scope for improvement in the future.

Figure 5. Original Image (First-Left) and its obtained Fuzzy Clustered Images

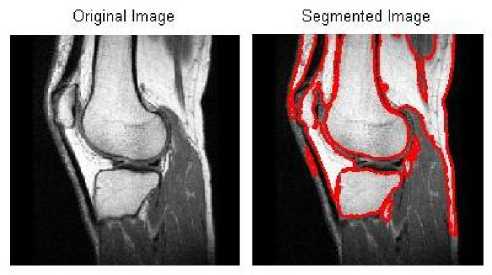
Figure 6. Original Image (Left) and Segmented Image (Right) Obtained Using Fuzzy Cluster Number 3 (Figure No. 3, Right Side ) in Proposed Hybrid Approach