A Hybrid PSO-GSA Approach for Cluster Head Selection and Fuzzy Logic Data Aggregation in DEEC-based WSNs

The development of the Internet of Things (IoT) has drawn significant attention to the field of WSN research in recent years. These networks' utilization of sensor nodes gives them a chance to stand out and be employed in a variety of applications. Physical events including pressure, temperature, and moisture can all be detected and tracked by these nodes. Moreover, sensors are unquestionably inexpensive and small-sized equipment as a result of the industry's development. The aforementioned characteristics facilitate the ubiquitous integration of these entities, allowing software applications to harness their multitude in vast quantities. Various domains such as industrial surveillance and management [1, 2], logistics and transportation [3, 4], intelligent infrastructure [5, 6], and healthcare [7, 8], exemplify the diverse applications of WSNs.

WSNs encompass two distinct network models: homogeneous and heterogeneous networks. Homogeneous networks entail sensor nodes within the WSNs possessing identical physical and software attributes. Heterogeneity is when the nodes of the network are different from each other. Generally, researchers use heterogeneity in different knot energy levels. Heterogeneous WSNs have been developed because homogeneous based algorithms do not work very efficiently on issues such as energy consumption and dispersion, and CH selection.

WSN can be formed by thousands of nodes working collaboratively. The generated data (from sensing), regardless of the logical topology used, converge towards a collection point, called the base station. The algorithms found in the literature (in general) follow two models: flat routing and hierarchical routing [9].

In the field of flat topologies, nodes enjoy unobstructed communication, assuming the responsibility of collecting and transmitting messages across multiple hops. This routing framework often generates a substantial number of transmissions owing to the extensive interconnectivity within the network. Consequently, routing algorithms must incorporate techniques that mitigate energy dissipation during communication, such as selecting an optimal path and minimizing transmission costs.

Diverging from the flat network structure, hierarchical networks appoint a specialized node known as the Cluster Head to aggregate data sent by other nodes in the network. Unlike flat networks, nodes within hierarchical networks transmit their data exclusively to their respective Cluster Heads, who then undertake the task of forwarding the most pertinent data to the Base Station. Hierarchical routing protocols exhibit enhanced adaptability and energy conservation [10, 11].

While wireless sensor networks offer numerous advantages, they also present certain design challenges. The foremost obstacle arises from the limited lifespan of sensors' small batteries. Consequently, researchers consistently seek energy-conscious communication methods as a remedy.

Furthermore, selecting an appropriate application distribution strategy poses another challenge in WSNs. Typically, two deployment techniques are employed: planned deployment and random deployment. In planned deployment, nodes are strategically positioned based on prior research conducted in the target area. On the other hand, random deployment serves as a simpler and cost-effective strategy but introduces its own set of challenges, including the clustering procedure.

The significance of the clustering process stems from its influence on the entire communication cycle. It contributes to subsequent stages of communication, such as data aggregation and routing. Data aggregation plays a crucial role in networks where energy conservation is paramount, as it minimizes the number of data transmissions. By organizing sensors into clusters, Cluster Heads assume the responsibility of aggregating sensed data from multiple source nodes within their cluster. Moreover, routing techniques must identify a reliable path from the multitude of available paths to reach the final sink, primarily the Base Station (BS) of the network. To simplify this route discovery process, data is routed solely between Cluster Heads. Consequently, effective clustering and routing techniques can achieve the desired outcome when sensors within the network are suitably clustered. As a result, clustering enhances overall network efficiency and remains a subject of great interest in research endeavors.

In applications deployed randomly, clustering assumes pivotal importance, considering the presence of numerous scattered nodes that must communicate with each other within an energy-constrained infrastructure. This methodology serves to group the deployed sensors, with each group led by a designated Cluster Head (CH) node tasked with overseeing group communication.

Within this research, we propose a fresh approach for cluster head selection within the Distributed Energy-Efficient Clustering (DEEC) algorithm. Our proposed approach leverages the hybrid optimization algorithm, Particle Swarm Optimization-Gravitational Search Algorithm (PSO-GSA), and incorporates fuzzy logic for data aggregation.

The primary contribution of our proposed approach is the utilization of PSO-GSA for CH selection in DEEC. By leveraging the strengths of both PSO and GSA algorithms, our approach can optimize the selection of cluster heads in a distributed manner, considering various performance metrics such as energy efficiency, network coverage, and load balancing. This hybrid optimization approach can provide a unique and effective solution to the CH selection problem in DEEC.

Moreover, we introduce the use of fuzzy logic for data aggregation to minimize the redundancy in the node transmission data, which can handle uncertain and imprecise sensor data in a wireless sensor network (WSN) more efficiently. By applying fuzzy logic to the data aggregation process, our proposed approach can result in more accurate and efficient aggregation of sensor data, leading to better overall performance of the WSN.

The novelty and originality of our proposed approach lie in the hybrid utilization of PSO-GSA for CH selection and fuzzy logic for data aggregation. Through extensive simulations and analysis, we demonstrate the effectiveness and superiority of our approach over existing methods. Our proposed approach can contribute to the advancement of the field of WSNs and optimization techniques, particularly in the context of energy efficiency and data aggregation.

While the hybridization of PSO and GSA for cluster head selection represents a novel aspect of the approach, additional clarity is required concerning other distinguishing features. One key aspect that sets the proposed methodology apart is the incorporation of fuzzy logic for data aggregation within the context of DEEC. Unlike traditional approaches, which may rely solely on deterministic methods for data aggregation, the utilization of fuzzy logic enables the handling of uncertain and imprecise sensor data more efficiently. This integration allows for a more robust aggregation process, resulting in improved accuracy and efficiency in data transmission. Furthermore, the approach emphasizes a distributed optimization strategy, leveraging the strengths of PSO-GSA to optimize cluster head selection while considering various performance metrics such as energy efficiency, network coverage, and load balancing. By combining these elements, the methodology offers a comprehensive solution that addresses the challenges of energy efficiency and data aggregation in wireless sensor networks, thereby advancing the field beyond existing methodologies.

Real-World Applications:

• •    The proposed methodology, integrating a hybrid optimization algorithm of Particle Swarm Optimization and Gravitational Search Algorithm alongside fuzzy logic for data aggregation in wireless sensor networks, carries substantial implications for real-world applications.

• •    This research addresses critical challenges prevalent in various domains, including but not limited to industrial automation, environmental monitoring, smart agriculture, healthcare systems, and infrastructure management.

• •    By optimizing cluster head selection and enhancing data aggregation efficiency, the study offers potential solutions to improve energy efficiency, reliability, and adaptability in wireless sensor network deployments.

• •    In industrial automation, the optimized methodology can streamline monitoring and control processes, leading to enhanced operational efficiency and cost savings.

• •    Environmental monitoring applications can benefit from more accurate and timely data collection, enabling proactive measures for pollution control, natural disaster management, and climate change mitigation.

• •    In smart agriculture, the proposed approach can facilitate precision farming techniques, optimizing resource utilization, crop yield, and overall farm productivity.

• •    Healthcare systems stand to gain from improved monitoring and management of patient health parameters, enabling remote patient monitoring, early disease detection, and personalized treatment strategies.

• •    Infrastructure management applications can leverage the optimized methodology for efficient monitoring of critical infrastructure assets such as bridges, dams, and pipelines, enhancing safety and reducing maintenance costs.

2.    Literature Review

The study begins by providing a comprehensive literature review in Section II, highlighting the relevant research in the field. The materials and methods used in the research paper are presented in Section III. In Section IV, the proposed methods are explained in detail. The results of the MATLAB-based simulation are presented and analyzed in Section V. Finally, the paper concludes with a summary of the findings and conclusions in Section VI.

The potential applications and associated challenges of WSNs have garnered significant attention from researchers. These networks find utility in diverse fields such as military operations, environmental monitoring, medical research, scientific investigations, health applications, and area and structural health monitoring. However, they simultaneously face a multitude of difficulties, including simplicity of deployment, wide coverage, seamless connectivity, scalability, robustness, fault-tolerance, security, and efficient energy utilization. One of the major challenges lies in extending the network's lifespan to enable continuous monitoring of the target area for object activity. The effective management of network energy directly impacts the longevity of the network. Consequently, various strategies and protocols have been devised to address this concern. In 2000, Heinzelman et al. introduced LEACH (Low Energy Adaptive Clustering Hierarchy) [12], the pioneering protocol for prolonging the lifespan of WSNs.

LEACH, being a popular clustering-based protocol, involves the partitioning of sensors into groups known as clusters. Each cluster is headed by a master node called the cluster head, responsible for collecting data from the cluster members and relaying it either directly to the base station or through intermediary nodes. The term "hierarchical protocol" refers to the characteristic of all sensors transmitting their data through cluster heads instead of directly to the base station.

LEACH encounters two primary challenges. Firstly, due to random selection, the cluster heads may not be evenly distributed across the entire network area. Secondly, the number of cluster head nodes is not fixed, leading to stochastic outcomes. To address these issues and enhance performance, LEACH-C and fixed LEACH [13] have been proposed. LEACH-C incorporates a base station (BS) that organizes the nodes and manages the network. Each round of LEACH-C requires nodes to communicate their remaining energy and positional data to the BS [14]. Leveraging this information, the BS can evenly distribute the cluster heads across the network topology and adjust the size of each cluster accordingly.

The base station (BS) plays a crucial role in energy-demanding tasks like cluster creation and cluster head selection. Additionally, it adjusts the probability of selecting cluster heads based on the remaining energy of individual nodes. Fixed-LEACH maintains a fixed number of cluster heads. While sensor nodes choose the nearest cluster head, each cluster head may accommodate a varying number of nodes, resulting in uneven energy dissipation. To address this, the LEACH approach was enhanced and rebranded as "power efficient collecting in sensor information systems" (PEGASIS) [15]. PEGASIS protocol is exceptionally suitable for data-gathering applications due to its efficient energy usage. The fundamental concept of PEGASIS involves connecting sensor nodes in a chain, allowing each node to communicate with and relay data to its nearest neighbor. The acquired data is passed between nodes, fused, and subsequently transmitted to the base station by a designated node (BS). To minimize the average energy consumption per node per round, nodes take turns broadcasting to the BS. However, due to significant delays, PEGASIS is not ideal for large-scale networks [15].

Another hierarchical clustering-based protocol discussed by Manjeshwar et al. is the threshold-sensitive energyefficient sensor network (TEEN) protocol [16]. In this protocol, the cluster head broadcasts hard and soft thresholds for detected properties to the nodes. The hard threshold dictates that a sensor node must possess a minimum attribute value to activate its transmitter and send data to the cluster head. Consequently, the hard threshold restricts broadcasting to instances when the range of the sensed property is of interest, thereby significantly reducing transmissions. The soft threshold further minimizes transmissions in scenarios where the value of the sensed property remains relatively unchanged [17]. However, TEEN is not recommended for applications that require periodic reporting, as certain consumers may not receive any data if the criteria are not met [18].

The adaptive threshold-sensitive energy-efficient sensor network (APTEEN) protocol was developed as an extension of the TEEN protocol [19]. APTEEN is specifically designed for recording time-sensitive events and continuous data collection. Users can define a count time interval and set threshold values. However, APTEEN suffers from overhead and complexity in cluster formation [20].

Authors in [21] introduce the hybrid energy-efficient distributed (HEED) clustering technique, which is a modification of the LEACH protocol. HEED employs two parameters to select cluster heads: residual energy serves as the primary criterion, while the node's degree serves as the secondary criterion. The degree of a node and the number of nodes within its range aid in load balancing and distributing workload among cluster heads. HEED exhibits low processing time and message exchange overhead and makes no assumptions regarding node dispersion or geographic awareness [21, 22].

For the past few years, the focus of research on wireless sensor networks (WSNs) has primarily revolved around homogeneous WSN technologies, where all nodes share the same system resources. However, there has been a recent surge in the popularity of heterogeneous wireless sensor networks. According to several studies [23, 24, 25], incorporating heterogeneous nodes can enhance network stability and lifespan without significantly increasing costs. Although heterogeneous nodes are more expensive compared to homogeneous nodes, they excel in data filtering, fusion, and transmission. A heterogeneous node can possess diverse resource categories, such as enhanced communication or energy capacity. They may feature a more powerful microprocessor, greater memory, or both, in comparison to standard nodes. Additionally, they can utilize high-bandwidth, long-range networks for communication with the base station. The introduction of heterogeneous nodes extends the network lifetime and enhances network energy efficiency [26, 27].

Various papers have covered heterogeneous network models, including the Stable Election Protocol (SEP) [28], which is an extension of LEACH that leverages heterogeneity. This protocol was among the first to explore heterogeneity. It employs a weighted election probability based on the nodes' remaining energy to ensure balanced energy utilization among nodes. The SEP introduces two levels of heterogeneity: normal nodes and advanced nodes [29].

The Single-Hop Energy-Efficient Clustering Protocol (S-EECP) and the Multi-Hop Energy-Efficient Clustering Protocol (M-EECP) are two distributed protocols discussed in [30] and [31], respectively. In S-EECP, the selection of cluster heads is based on a weighted probability determined by each node's residual energy proportional to the network's average energy. The authors observed that nodes located farthest from the base station experienced higher energy consumption due to long-distance transmission. In single-hop communication, where data packets are directly transmitted to the base station without relay nodes, these distant nodes may deplete their energy faster. M-EECP resolves this issue by employing multi-hop communication to the base station [32]. M-EECP solves the single-source shortest problem using a greedy strategy to determine the shortest route from each cluster head to the base station.

The authors of [33] discuss a Stable and Energy-Efficient Clustering (SEEC) technique, which is further expanded to Multi-Level SEEC [33, 34]. SEEC relies on a clustered network structure, where each cluster contains a robust advanced node and a few standard nodes randomly placed within. In multi-level architectures, more powerful super nodes are responsible for covering remote sensing areas. Each type of node performs specific functions in sensing, aggregation, or transmission to the base station.

A Heterogeneous HEED approach for WSNs is described in [35-37], taking into account three factors: distance, node density, and residual energy. Fuzzy logic is employed to determine the cluster heads [36]. However, data loss may occur in this protocol if cluster heads are unable to interact with one another [37]. An adaptation of [35], which utilizes fuzzy logic and provides an energy-efficient approach for heterogeneous WSNs, is proposed by the authors in [36]. The protocol considers residual energy, node density, distance, and the distance between the base station and the sensor as the four factors. Cluster heads are selected using fuzzy logic. Similar to the previous protocol, data loss may occur if cluster heads cannot communicate with each other. The authors of [37] present a multi-layer heterogeneous network model for WSNs, extending up to seven levels. It incorporates four fuzzy clustering criteria, including residual energy, node density, distance, and the separation between the base station and the sensor.

In [38], the authors discuss a Cell-Clustered Algorithm for Energy Efficiency (CC-HEED), which is an extension of the HEED protocol [21]. The core cluster regions of the network are divided into several cell-shaped sections in CC-HEED, where cell nodes are placed strategically to gather data within each cell area while considering power consumption models. The energy consumption issues observed in PEGASIS are addressed by employing the Concentric Clustering Algorithm (CCS). CCS leverages the location of the base station to enhance performance and prolong the network's lifespan [39].

To extend the network lifetime in WSNs, the authors of [40] propose an Energy-Efficient Clustering Protocol (NEECP). This technique selects cluster heads efficiently by incorporating a flexible sensing range and a chaining method. Additionally, it employs a redundancy check algorithm to prevent the transmission of redundant data, thereby prolonging the network's lifespan [41]. The protocol considers both aggregated and non-aggregated data. The DEEC protocol is used to estimate the network lifetime in our suggested network models. In another study, the authors of [42] introduce a new routing algorithm based on LEACH, which optimizes the clustering mechanism. Furthermore, the authors of [43] present the Hybrid Energy-Efficient Distributed Clustering (HEED) protocol. According to this protocol, the selection of cluster heads periodically takes into account factors such as the remaining energy of nodes, neighbors, and secondary parameters like node degree [44].

In a different study, the authors of [45] evaluate the network's lifetime and propose the EDEEC protocol derived from DEEC to enhance its stability. This algorithm reduces network heterogeneity while increasing energy levels. Subsequent researchers [46-50] provide several protocols that support DEEC-derived tri-level heterogeneity. The authors of [46] propose a Three-Level Energy-Efficient Heterogeneous Clustering Method (DEEC) as a distributed energyefficient clustering protocol. Unlike other works, this study incorporates a balance-based threshold in the energy consumption model.

3.    Materials and Methods 3.1.    Fuzzy Logic

Fuzzy logic is a mathematical tool renowned for its effectiveness in handling uncertainty and imprecision. Unlike classical set theory, which deals with precise and binary values, fuzzy logic allows for intermediate values or degrees of membership within a set. Fuzzy logic finds extensive application in modeling complex systems, especially in the realms of engineering and decision-making.

There are two primary types of fuzzy inference mechanisms: Mamdani and Sugeno. The Mamdani mechanism employs a collection of fuzzy rules to determine the membership degree of each input variable in a fuzzy set. These membership degrees are subsequently aggregated to yield a single output value. In contrast, the Sugeno mechanism generates a linear function of the input variables, where each rule contributes a weighted linear term to the final output.

A typical fuzzy system comprises four key components: the fuzzification module, the fuzzy rules base, the fuzzy inference engine, and the defuzzification module. The fuzzification module converts crisp input values into corresponding fuzzy sets, assigning each set a specific membership degree. The fuzzy rules base consists of a set of rules, often formulated in the If-THEN format, that establish the relationship between fuzzy inputs and fuzzy outputs. The fuzzy inference engine utilizes these rules to calculate the membership degree of the outputs. Finally, the defuzzification module transforms the fuzzy output into a crisp value.

Fuzzy logic has found widespread applications across various domains, including control systems, pattern recognition, decision-making, and optimization. Its remarkable capability to handle uncertainty and imprecision makes it highly valuable in scenarios where conventional mathematical models may not suffice.

The innovative application of fuzzy logic in this context involves its integration into the data aggregation process within wireless sensor networks. Specifically, fuzzy logic is employed to bridge the gap between crisp, deterministic sensor data and the inherently uncertain real-world phenomena being measured. By representing sensor readings as fuzzy sets with membership functions, fuzzy logic enables a more flexible and adaptive approach to data aggregation. This means that instead of treating sensor data as strictly true or false, fuzzy logic allows for the representation of data with varying degrees of certainty or ambiguity.

Furthermore, the utilization of fuzzy logic within the proposed methodology extends beyond mere data representation. Fuzzy rules are formulated to govern how sensor data is aggregated and interpreted within the network. These rules capture the expert knowledge and domain-specific heuristics that guide the aggregation process, allowing for more contextually relevant decision-making.

Moreover, the integration of fuzzy logic introduces a layer of adaptability and robustness to the data aggregation process. Fuzzy inference mechanisms, such as the Mamdani and Sugeno models, enable the aggregation of sensor data in a manner that is responsive to changing environmental conditions and network dynamics [52]. This adaptive approach ensures that the network can effectively handle uncertainties and variations in sensor readings, leading to more reliable and accurate data aggregation results.

• 3.2.    PSO-GSA

The hybrid optimization approach known as PSO-GSA combines the principles of PSO and GSA to enhance the process of cluster head selection in DEEC WSNs for improved energy efficiency. DEEC is a commonly employed clustering technique in WSNs, where sensor nodes autonomously form clusters, with a rotating cluster head (CH) tasked with collecting data from cluster members and transmitting it to the base station (BS).

Let's designate the overall energy of the network as E and the energy of each node in the network as E_t, where i represents the node index. The energy consumption of a node is influenced by its proximity to the BS and its role within the clustering procedure.

In DEEC, network nodes are allocated into clusters, with one node serving as the CH and the remaining nodes as cluster members. The CH assumes the responsibility of aggregating and processing data from cluster members before relaying it to the BS. To optimize the CH selection process, the PSO-GSA algorithm, which incorporates techniques from PSO and GSA, can be employed.

Let X¹ ^ and V ¹⁷' denote the position and velocity of particle i in dimension j at iteration t, while X_best and F_best represent the best position and fitness value achieved by the swarm thus far. The fitness function f(p) is evaluated based on the performance of the Energy model, which considers the distance from the BS and the node's role as a CH. The energy consumption model can be defined as follows:

E_t = E_bs + E_agg(d T )

Here, E_t signifies the energy of node i, E_bs denotes the energy consumption at the BS, E_agg represents the energy consumption for data aggregation, and d [ indicates the distance between node i and the BS.

The hybrid PSO-GSA algorithm updates the position and velocity of each particle using the following equations:

V ^iJ (t + 1) = wVⁱ\t) + С 1 Г 1 * (X^t) - X4(t)) + c₂r₂ (X b _est(t) - X^'(t))                       (2)

X^{l 1} (t + 1) = X ‘J (t) + VV(t + 1)

In these equations, w denotes the inertia weight, С 1 and c₂ represent the acceleration coefficients, r 1 and r₂ are random numbers between 0 and 1, X_best signifies the best position of particle i in dimension j obtained thus far, and X_best denotes the best position achieved by the swarm. The GSA algorithm updates the position of each particle using the following equation:

X^(t + 1) = X^;(t) + G ^iJ (t)                                            (4)

Here, G¹¹ (t) denotes the gravitational force acting on particle i in dimension j at iteration t, which is calculated as:

G ^iJ (t) = G (^) (^(t) - X ‘ (t)) + G (g) (X^g(t) - X^t)) + ap                    (5)

Within this equation, G represents the gravitational constant, M¹ signifies the mass of particle j , R^ denotes the distance between particle i and particle j, X¹ indicates the position of particle j , R_g represents the distance between particle i and the global best solution, X^g denotes the position of the global best solution, a represents a random perturbation, and p is a random number drawn from a Gaussian distribution with a mean of 0 and a standard deviation of 1.

• 3.3.    Basic Network

• •    Sensor Node: The basic part of any WSN is known as sensor node, it is an electronic device capable of sensing and transmitting information to its neighbouring nodes and base station. It has several responsibilities during network operation such as: sensing, data storing, data processing and transmission.

• •    Cluster: A cluster can be visualized as an assemblage of sensor nodes within a wireless network. It is common for a wireless sensor network to consist of a large number of nodes, sometimes numbering in the thousands. In order to facilitate their efficient operation, these nodes are subdivided into smaller groups referred to as clusters.

• •    Cluster head: Cluster head node is leader node if the corresponding cluster. It is responsible for successful and efficient operation of its cluster.

• •    Base Station or Sink: Base station or Sink node is at the topmost level of clustering hierarchy. It provides connectivity between end user and sensor nodes as well as it is responsible for controlling the operation of entire WSN.

  
  
  

• 3.4.    Distributed Energy-efficient Clustering (DEEC)

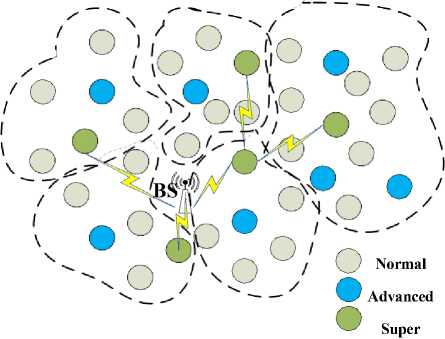
Fig.1. Clustered heterogeneous network structure [8]

The DEEC protocol employs a probabilistic approach to choose its cluster heads, considering both the remaining energy of the nodes and the average energy of the network. In contrast to certain proposed clustering methods, the rotation of Cluster Heads is determined based on the residual energy of the nodes. Similarly, in the proposition presented in this study, the node with the highest energy level possesses a higher likelihood of being elected as the leader of the group. The incorporation of network heterogeneity by the authors of DEEC pertains to the energy capacity of a specific set of nodes constituting the network. The outcomes demonstrate that the introduction of two levels of heterogeneity and the selection of the Cluster Head based on the initial and residual energy of the nodes contribute to an extended stability period and increased network lifespan. Similar to most algorithms derived from the LEACH algorithm, DEEC relies on local information without considering node positioning when selecting cluster heads in the network [51].

The DEEC estimates the head node selection probability in multilevel heterogeneous WSNs according to the following formula:

Е^—ЕСт)!        е^г)

Pi    Popt [1       E(r~)    |    Popt E(r)(6)

At the same time, in the DEEC algorithm, the average network energy E(r) for an arbitrary round r is calculated as:

W)=l£totai(1 — r)(7)

tv

In this context, R represents the overall duration of network operation and is evaluated using the following method:

^ _ Cotati

^E round

Where, E_total is the total energy in the network, and E_round is the energy consumption during the round.

• 3.5.    Energy Model

In a prior investigation, clustering algorithms proved inadequate in ensuring consistent clusterhead selection during simulation. By incorporating a stable clusterhead selection criterion based on the number of active nodes in the field during a specific round, it is possible to reduce energy consumption in the network and improve overall network performance. Building upon this concept, we introduce an intelligent clustering algorithm aimed at prolonging the network's lifespan. Let us examine the radio energy dissipation model illustrated in Fig.2.

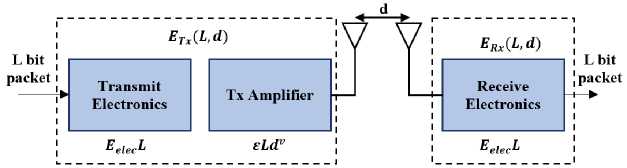
Fig.2. Model for radio energy dissipation

The energy expended by the radio in achieving a satisfactory SNR while transmitting L-data bits over a distance D can be calculated using the following equation:

ETx(l,d-)={

'L.E_elec t + L.e_fs.d² ifd0

Here, E_elect represents the energy dissipation per bit of the transmitter or receiver circuit, £ f _s and e_mp are dependent on the transmitter amplifier model, and d represents the distance between the receiver and transmitter.

By substituting d = d₀ in equation (9), we can determine:

d₀=                                                      (10)

\ ^mp

Therefore, the energy consumed by the receiver to receive an L-bit message is given by:

E_Rx = L. E elect                                                      (11)

Let us assume that the field area is A x A square meters, and there are 100 nodes uniformly distributed across the field. For the sake of simplicity, let's assume that the sink node is located at position (50, 50), and no node is situated farther than d₀ from the sink node. Consequently, the energy dissipation of a clusterhead node during a round can be calculated as:

ech

= EE_elect ( П -1)

n

+ ^{L. E}DA ^+ ^{L. E}elect

+ L. € f _s. ^dtoBS

In this equation, к represents the number of clusters, E_DA denotes the data aggregation cost, and d_toBS is the distance between the clusterhead and the sink.

The energy dissipation of a normal node (non-CH) can be expressed as:

Whereas d_toCH represents the distance between a normal node and its clusterhead. By combining equations (12) and (13), we can express the energy dissipation of a cluster as follows:

n

^Ecluster ~ ^ECH + ^ ПОпопСН

Furthermore, the total energy dissipation of the network can be calculated using the following equation:

^ЕТ .

= L. (2n ^E _e i _ect + ^ ^eda + ^ fs ^{(k. d toBS} + n _2лЛ))

4.    Proposed Work

This research paper introduces a novel methodology for clustering in wireless sensor networks by utilizing the DEEC algorithm, augmented with the PSO-GSA.

The primary objective is to enhance the selection process of cluster heads within DEEC by harnessing the synergies between PSO and GSA. This approach aims to achieve optimized CH selection, emphasizing energy efficiency and network coverage. DEEC is a well-established algorithm in WSNs that effectively prolongs the network's lifetime by judiciously utilizing sensor node energy resources. Nevertheless, the conventional DEEC algorithm may not consistently yield the most optimal CH selection, thereby impacting overall network performance. To overcome this limitation, we introduce the hybrid PSO-GSA methodology, merging the exploration capabilities of PSO with the optimization prowess of GSA. By integrating these two algorithms, our objective is to enhance the CH selection process in terms of energy efficiency and network coverage. The PSO-GSA algorithm enriches the decision-making process for CH selection, taking into account multiple objectives and optimizing the trade-off between energy consumption and network coverage.

Furthermore, in our proposed approach, we incorporate fuzzy logic for data aggregation. Fuzzy logic proves to be a valuable tool in effectively managing the uncertainty and imprecision inherent in sensor data, thereby enhancing the accuracy and efficiency of data aggregation within the WSN.

In order to assess the performance of our proposed methodology, we undertook extensive simulations and conducted a comparative analysis against existing techniques. The outcomes validate the efficacy and supremacy of our hybrid approach with respect to energy efficiency, network coverage, and overall network performance. Our approach surpasses current methods in terms of network longevity, accuracy of data aggregation, and energy utilization. Our research contributes to the progress of WSN and optimization methodologies by presenting a distinctive and authentic approach that amalgamates the PSO-GSA for cluster head selection, along with fuzzy logic for data aggregation. The amalgamation of these techniques enhances the overall performance of WSNs in relation to energy efficiency, network coverage, and accuracy of data aggregation.

The classification of nodes into primary and secondary categories is determined by their proximity to the base station, as visually represented in Fig.4. These nodes subsequently establish primary and secondary clusters. The election of cluster heads within these clusters occurs based on their weighted probabilities. Both primary and secondary cluster heads undertake the task of aggregating data received from their respective cluster members. While primary cluster heads transmit their aggregated data directly to the base station, this transmission process presents a significant energy consumption challenge for secondary cluster heads. This is due to the direct relationship between the energy required for data transmission and the square of the distance separating the transmitter and receiver. Consequently, in order to alleviate this energy burden, secondary cluster heads search for nearby primary cluster heads and forward their data to them. The primary cluster heads then route this data to the base station without applying any data aggregation techniques. Furthermore, the benefits of clustering destinations, such as reduced delay, fault tolerance, maximal network longevity, minimum cluster count, increased connectivity, and load balancing, are also elucidated in the context of homogeneous wireless sensor networks.

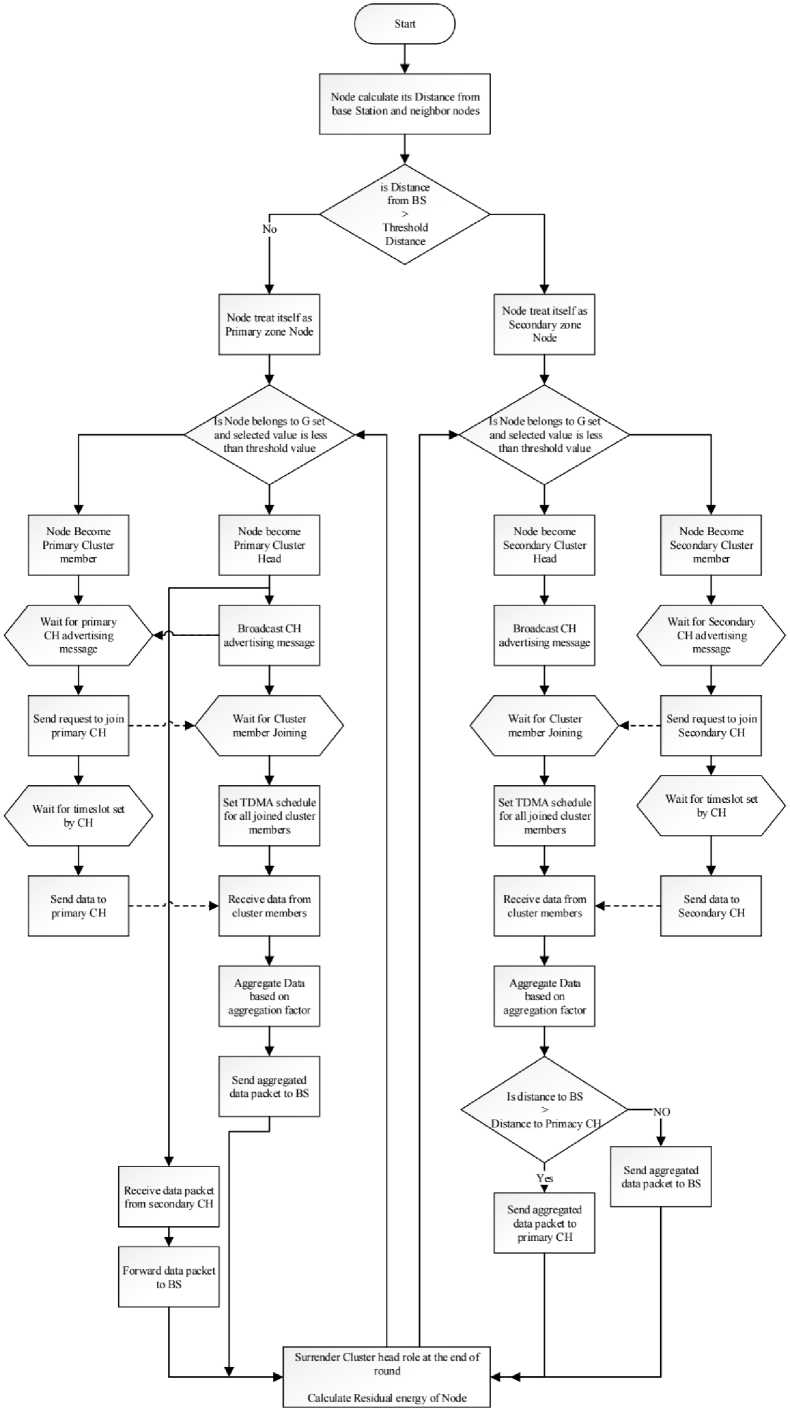
Fig.3. Flow of proposed WSN according to primary and secondary cluster head

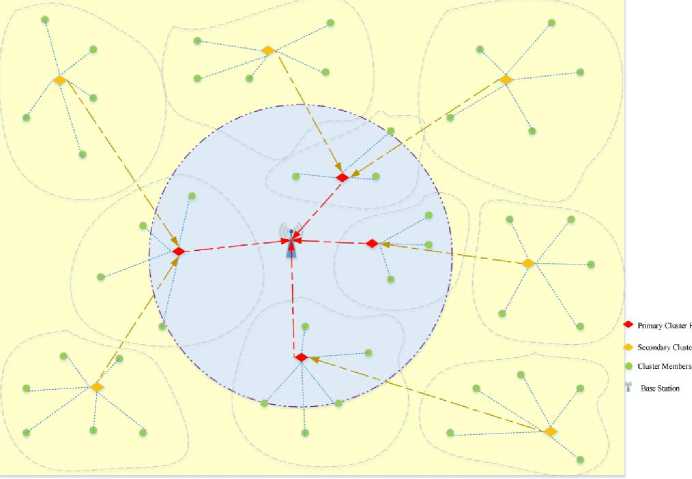
Fig.4. Hierarchical clustering methodology aimed at enhancing energy efficiency in wireless sensor networks during data aggregation

• 4.1.    Phase 1: Improved Cluster Head Formation Scheme

We have enhanced the DEEC protocol by incorporating two additional stages in the process of cluster head selection. The network region is divided into two distinct sections, namely the primary area and the secondary area. The basis for selection lies in the proximity of the node to the base station. If the distance is below 30 meters (considered as the threshold value), the node will be designated as part of the primary zone. Conversely, if the distance exceeds this threshold, the node will be categorized as a secondary node. During the selection of cluster heads, clusters are formed separately for primary and secondary nodes.

A typical architecture of clustering process is shown in Fig.5.

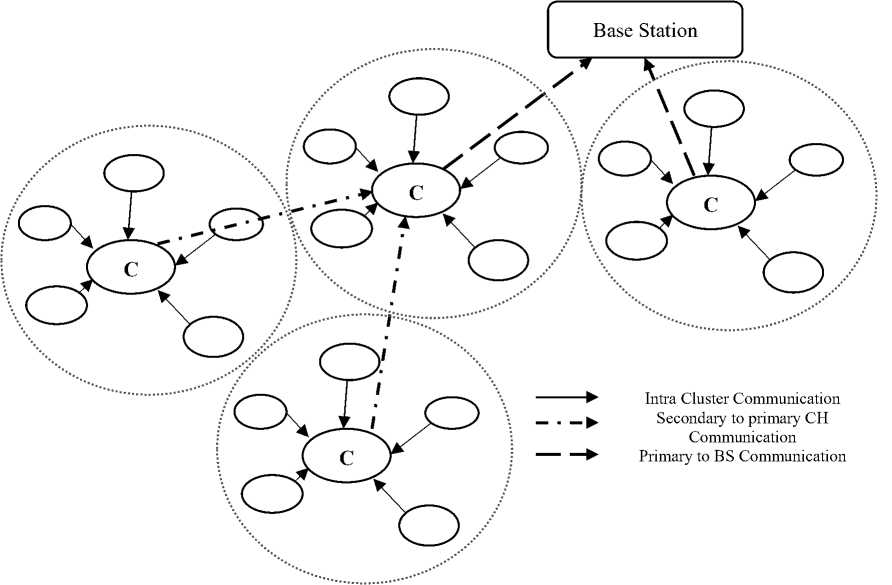
Fig.5. Data transmission within a clustering network

Each node, denoted as s ^ , employs a probability threshold to determine its eligibility as a cluster-head in each round. The threshold function is expressed as follows:

t ⁽ sd

{

P i 1-P i x(r mod-¹)

ifnEG

0, otherwise

Here, P i represents the weighted probability of a node becoming a cluster-head. The weighted probabilities for normal and advanced nodes are defined as follows:

For normal nodes:

p    _ Poyt PiG} lnrm — 1+a.m E(r)

For advanced nodes:

p    _ ^Popt ( ^1+a ) E i (r)

^ladv -   1+a.m E(r)

Additionally, the optimal probability for a node to be elected as a cluster-head is determined by:

к p =

n

Taking into account equation (19) and incorporating the concept of alive nodes, the optimal number of cluster-heads (K_opt) can be derived based on the number of alive nodes (n_allve) during the current round:

K opt = ^p * ⁿallve                                                 ⁽²⁰⁾

In equation (20), K_opt represents the optimal number of cluster-heads required for any given round, while n_a i _lve denotes the number of alive nodes in the network during that round. The value of K_opt depends on the cluster-head election probability (p) and the number of alive nodes in each round. It is important to note that the number of alive nodes cannot be considered as a network input. Therefore, the problem of optimized cluster-head election can be simplified by finding an optimal cluster-head election probability that maximizes the network's lifetime according to Equation (20). The network's lifetime, measured by the number of dead nodes present during each round, can be optimized using a genetic algorithm. This research utilizes a genetic algorithm to identify the optimal cluster-head election probability that minimizes the number of dead nodes.

The optimized cluster-head election probability is denoted as p_opt , and Equation (20) can be rewritten as:

^Kopt = ^popt * ⁿallve

The dual energy of the nodes indicates the influence of a node's energy on the election probability. It is computed as:

f(E_Res) = ~ ^Pavg

Here, E_avg represents the average residual energy of sensor nodes in each round.

By observing Equation (22), we can note that the enhanced threshold function employs the residual energy of nodes for the cluster-head election process. This approach ensures that only nodes with a certain amount of remaining energy are selected as cluster-heads, resulting in a balanced cluster-head election. In conventional clustering schemes, cluster formation is based on the minimum distance criterion. Nodes that are not chosen as cluster-heads transmit their data to either the nearest cluster-head node or directly to the base station, without considering the energy level of the cluster-head node or its distance from the base station. To address this limitation, this research proposes an improved cost functionbased cluster-formation scheme. After the successful election of cluster-head nodes, each non-cluster-head node calculates the cost function value for each contender cluster-head node and forwards its data to the node with the minimum cost function value. The cost function for the proposed cluster-formation scheme is defined as follows:

^dij , p Resd) , DU)

C ^ost(i ,]) = -    * -  — * -                                            ⁽²³⁾

^dmax   ^PRes^(j J   ^Davg

In equation (23), d_l j represents the distance from node S_l to cluster-head C j , while d_max represents the maximum distance from S_l to the candidate cluster-heads. E_Res(i) and E_Res(j) denote the residual energy of node S_l and clusterhead C j , respectively. D(j) represents the distance from cluster-head C j to the base station, and D_avg signifies the average distance between cluster-heads and the base station.

Algorithm 1:

function PSO_GSA()

Initialize PSO parameters and variables

Initialize GSA parameters and variables

Generate initial population for PSO and GSA while (stopping criteria are not met) do

Evaluate fitness of particles in the PSO population

Update PSO particle positions and velocities using PSO equations

Update PSO personal and global bests

Evaluate fitness of individuals equation (23) in the GSA population

Calculate gravitational forces on each individual using GSA equations

Update GSA individuals' positions and velocities

Combine PSO and GSA populations

Select the best individuals for next iteration return the best individual from the final population end function function ClusterHeadSelection()

Determine the number of cluster heads based on network parameters for each round in the DEEC algorithm do

Run PSO_GSA to select the cluster heads

Assign the selected cluster heads to the cluster heads array

Update residual energy of non-cluster head nodes return cluster heads array end function

• 4.2.    Phase 2: Proposed Data Aggregation Scheme

The primary factors contributing to energy consumption at cluster head nodes in a wireless sensor network include the energy expended in data transmission, data reception, and data aggregation. As per the radio energy dissipation model depicted in Fig.2, the energy utilization in wireless sensor networks is determined by the amount of information transmitted or received per meter. If every node, irrespective of their energy levels, were to transmit the same amount of information, nodes with lower energy reserves would deplete rapidly. To address this issue, this research endeavor introduces a data aggregation algorithm based on clipping. This algorithm trims redundant information from the original data packet based on the remaining energy level of the cluster head node and its distance from the base station node. Fig.6 portrays the architecture of the proposed FIS (Fuzzy Inference System) for the data aggregation algorithm.

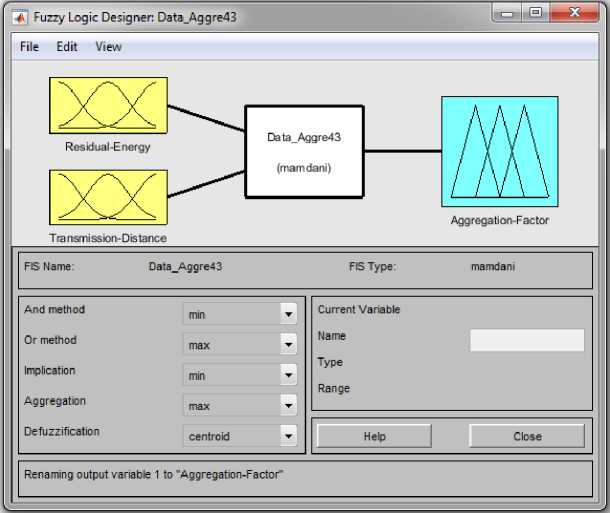
Fig.6. Proposed FIS model

The inputs to the FIS system encompass the residual energy (remaining energy of sensor nodes) and the transmission distance (distance between the cluster head node and the base station). The level of clipping is calculated using fuzzy logic, considering these input variables. The FIS system outputs an Aggregation-factor denoted by £ . Thus, Equation (15) can be restated as:

The value of £ ranges from 0 to 1, which corresponds to the proposed data aggregation scheme outputting clipped data within the range of 0% to 100%.

To prolong the network's lifespan, we categorized each linguistic variable associated with these parameters into three levels: low, medium, and high for the energy level of the cluster head; close, medium, and far for the distance to the base station and the distance between the cluster heads and the node. In MATLAB's fuzzy logic toolbox, we employed Triangular and Trapezoid membership functions to represent these linguistic variables. Equations (25) and (26) represent the Triangular and Trapezoid membership functions, respectively.

(  0, x-a b-a’

II — J c-x VA = \--

c-b

0, x-a b-a '

1 b-x

■ d-c

x < a a < x < b b < x < c c < x x < a a < x < b b < x < c d < x

Coordinates for each membership functions are:

Residual Energy Consider 3 membership functions

Low Energy [0, 0, 0.205, 0.499]

Medium Energy [0.197, 0.491, 0.53, 0.8056]

High Energy [0.507, 0.8003, 1, 1]

Distance Consider 3 membership functions

Close distance [0, 0, 20, 50]

Medium distance [20, 50.5, 80]

Far distance [50 ,74.74, 100, 100]

Table 1. Fuzzy rules for data aggregation factor

Sr. No.	Energy Level	Distance	Aggregation Factor
1	Low Energy	Close distance	High aggregation
2	Low Energy	Medium distance	High aggregation
3	Low Energy	far distance	High aggregation
4	Medium Energy	Close distance	Low aggregation
5	Medium Energy	Medium distance	Medium aggregation
6	Medium Energy	far distance	High aggregation
7	High Energy	Close distance	Low aggregation
8	High Energy	Medium distance	Low aggregation
9	High Energy	far distance	Medium aggregation

A set of fuzzy rules for a proposed approach to data aggregation. These rules define how the "Fuzzy Output" level is determined based on the values of two input variables: "Residual Energy" and "Transmission Distance."

Residual Energy: The "Residual Energy" is categorized into six fuzzy sets, each representing a specific range of remaining energy, from 0-10% to 90-100%.

Transmission Distance: The "Transmission Distance" is categorized into three fuzzy sets: "Low," "Medium," and "Far." These sets likely represent different levels of distance or proximity between the data sources.

Fuzzy Output: The "Fuzzy Output" is represented as linguistic variables, such as "Level-0" to "Level-9." These levels likely indicate the strength or quality of the data aggregation process, with "Level-9" being the highest and "Level-0"

being the lowest. Following are the key features of proposed method:

Granularity of Input Variables : The partitioning of "Residual Energy" and "Transmission Distance" into multiple fuzzy sets allows for a more detailed and nuanced analysis of these variables. This granularity is useful when making decisions or aggregating data under varying conditions.

Output Levels: The "Fuzzy Output" levels suggest that the system can produce a range of different output levels based on the combination of "Residual Energy" and "Transmission Distance."

Rule Combinations: The table outlines how the "Fuzzy Output" level is determined based on specific combinations of "Residual Energy" and "Transmission Distance." For example, if the "Residual Energy" is in the range of 0-10% and the "Transmission Distance" is "Low," the "Fuzzy Output" level will be "Level-9."

To fully understand the significance of these rules, additional context is needed. The "Fuzzy Output" likely represents the quality, reliability, or some other metric of the data aggregation process. For example, "Level-9" could mean that the data aggregation process is of the highest quality and reliability when the "Residual Energy" is very low (0-10%) and the "Transmission Distance" is "Low" These fuzzy rules is applied within a fuzzy logic system to determine the appropriate level of data aggregation based on the real-time values of "Residual Energy" and "Transmission Distance." This approach allows for more flexible and context-aware decision-making, which can be particularly valuable in systems where conditions are not always binary or clear-cut.

By adding aggregation factor in DEEC protocol we modified DEEC protocol and propose our new model.

Fig.7. Proposed modified DEEC model

Algorithm 2

Input: Sensor nodes, Network parameters

Output: Selected Cluster Heads

Initialize the sensor nodes and network parameters

Define PSO and GSA parameters

Define FIS parameters function PSO_GSA_ClusterHead_Selection()

Initialize PSO and GSA parameters

Initialize the CH selection probabilities for all sensor nodes for each round in the DEEC algorithm do

Perform the PSO-GSA optimization process for CH selection

Calculate the fitness value for each sensor node using PSO and GSA for each sensor node do

Update the CH selection probability using the PSO and GSA fitness values end

Select the Cluster Heads based on the updated CH selection probabilities

Perform data aggregation and transmission for each Cluster Head

Calculate the residual energy and transmission distance for each Cluster Head for each Cluster Head do

Calculate the FIS input values using the residual energy and transmission distance

Apply the FIS rules and inference process to determine the data aggregation weight

Aggregate and transmit the data using the data aggregation weight end end

Return the selected Cluster Heads

End

In the suggested methodology, the transmission of data to both the primary and secondary Cluster Heads (CHs) entails employing the Fuzzy Inference System (FIS) incorporating the factors of remaining energy and transmission range. Now, let us delve into a comprehensive analysis of how data is transmitted to the primary and secondary CHs:

• 4.3.    Primary Cluster Head (PCH) Data Transmission

• •    Residual Energy Calculation: Each sensor node assesses its residual energy level, which indicates the remaining power. Typically, this metric is obtained by measuring the energy consumption during sensing and communication operations.

• •    Transmission Distance Calculation: The distance of transmission between every sensor node and the PCH is computed. This distance can be determined based on either the physical separation or the signal strength observed between the nodes.

• •    FIS Input Calculation: The calculated residual energy and transmission distance are employed as inputs for the FIS. These inputs are utilized to determine the appropriate weight for data aggregation assigned to the PCH.

• •    FIS Inference Process: The FIS applies pre-established membership functions, rules, and defuzzification techniques to the inputs. The membership functions capture linguistic variables representing energy and distance, while the rules establish the relationship between these variables.

• •    Data Aggregation Weight Determination: By analyzing the output of the FIS inference process, the data aggregation weight specific to the PCH is determined. This weight signifies the significance or contribution of the PCH in aggregating and transmitting data.

• •    Data Transmission: Sensor nodes aggregate their data based on the calculated data aggregation weight allocated to the PCH. Subsequently, the aggregated data is transmitted to the PCH for further analysis and processing.

• 4.4.    Secondary Cluster Head (SCH) Data Transmission

• •    SCH Selection: After determining the PCH, the remaining sensor nodes that are not chosen as the PCH engage in a competitive process to assume the role of the SCH. The selection criteria for the SCH may vary and typically consider factors such as residual energy, distance to the PCH, or network connectivity.

• •    SCH Residual Energy and Distance Calculation: The selected SCH calculates its own residual energy and determines the transmission distance between itself and the PCH.

• •    FIS Input Calculation: Similar to the PCH, the SCH utilizes its residual energy and transmission distance as inputs for the FIS.

• •    FIS Inference Process: The FIS carries out the inference process by employing predefined membership functions, rules, and defuzzification techniques to determine the data aggregation weight assigned to the SCH.

• •    Data Aggregation Weight Determination: The output generated from the FIS inference process indicates the data aggregation weight assigned to the SCH, signifying its contribution to the data aggregation and transmission procedure.

• •    Data Transmission: The sensor nodes associated with the SCH aggregate their respective data in accordance with the calculated data aggregation weight and transmit it to the SCH for further analysis and processing.

5.    Simulation and Results 5.1.    Simulation Parameter

• 5.2.    Performance Matrices

By incorporating the FIS system and considering the parameters of residual energy and transmission distance, the proposed methodology ensures that data transmission to both the primary and secondary CHs effectively accounts for these factors. Consequently, this approach facilitates efficient and optimized data aggregation within the Wireless Sensor Network (WSN), while also taking into consideration the energy limitations of the sensor nodes and the network's transmission characteristics.

In the subsequent section, MATLAB-based simulation results will be presented to validate the effectiveness of the proposed methodology.

Table 2. Simulation parameters

Parameter	Value
Sink location	(100, 100)
Radio range	17 m
Initial energy of node	20 J
Node	400
a	45 nJ/bit
a	135 nJ/bit
A	10 pJ/bit/m2
Rb	6m

• •    Stable Period: The duration between the initiation of the network and the cessation of functioning of the first node within the network.

• •    Unstable Period: The duration between the failure of the first sensor node and the failure of the last sensor node within the network.

• •    Network lifetime: The duration between the commencement of the network operation and the failure of the final active sensor node within the network.

• •    Throughput: The cumulative number of data packets successfully transmitted from nodes to the BS.

• •    Average Energy: The mean energy level across all nodes during a specified interval.

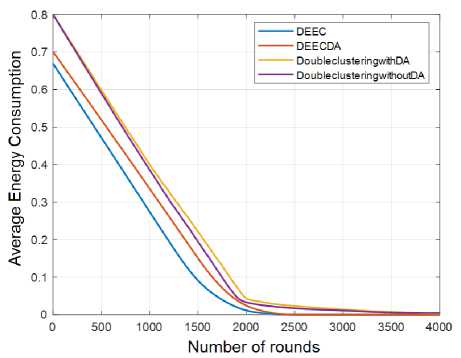
Fig.8. Comparative analysis of average energy consumption for various methods

Fig.8 presents a comparative analysis of average energy consumption for four clustering protocols: DEEC (Distributed Energy-Efficient Clustering), DEEC-DA (DEEC with Data Aggregation), Double Clustering with DA, and Double Clustering without DA. The graph provides insights into the energy efficiency of these protocols over a series of rounds in a wireless sensor network. The x-axis of the graph represents the number of rounds or iterations, indicating the progression of time within the network. It reflects the operational duration or the number of data exchanges that have occurred. The y-axis represents the average energy consumption, which represents the amount of energy consumed by the nodes participating in the network during each round. DEEC is a clustering protocol that aims to improve energy efficiency in wireless sensor networks. DEEC-DA is a variant of DEEC that incorporates data aggregation to reduce the amount of energy required for data transmission. Double Clustering with DA and Double Clustering without DA are additional clustering protocols that employ different strategies for load balancing and energy management. The graph compares the average energy consumption values for these four protocols. Each protocol is represented by a different line or data series on the graph.

Fig.9 presents a comparative analysis of the lifetime of four clustering protocols: DEEC (Distributed EnergyEfficient Clustering), DEEC-DA (DEEC with Data Aggregation), Double Clustering with DA, and Double Clustering without DA. The graph provides insights into the longevity and sustainability of these protocols by analyzing the number of dead nodes over a series of rounds in a wireless sensor network. The x-axis of the graph represents the number of rounds or iterations, indicating the passage of time within the network. It reflects the operational duration or the number of data exchanges that have occurred. The y-axis represents the number of dead nodes, which signifies the count of nodes that have exhausted their energy and are no longer operational.

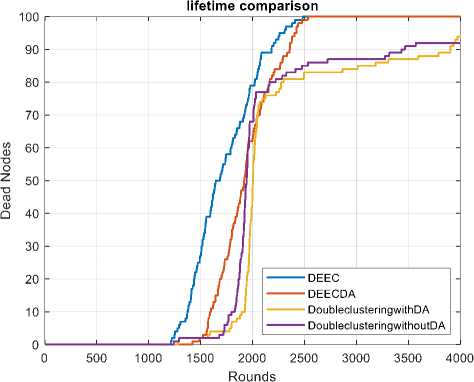
Fig.9. Comparative analysis of lifetime for various methods

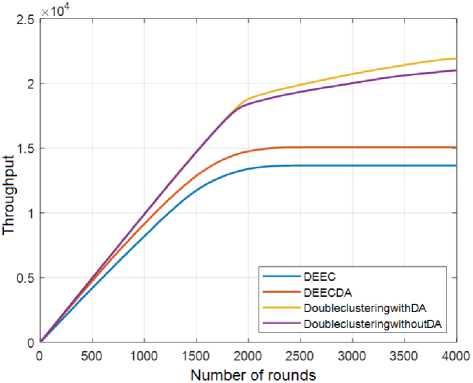
Fig.10. Comparative analysis of throughput for various methods

Fig.10 presents a comparative analysis of throughput for four clustering protocols: DEEC (Distributed EnergyEfficient Clustering), DEEC-DA (DEEC with Data Aggregation), Double Clustering with DA, and Double Clustering without DA. The graph allows for a comparison of the data transmission rates achieved by these protocols over a series of rounds in a wireless sensor network. The x-axis of the graph represents the number of rounds or iterations, indicating the progression of time or data exchange within the network. It reflects the operational duration or the number of data exchanges that have occurred. The y-axis represents the throughput, which indicates the rate of data transmission achieved by the protocols. It represents the amount of data successfully transmitted or received per unit of time. The graph shows that the throughput for all protocols initially increases with the number of rounds, but eventually the throughput stabilizes. It is clear that the double clustering with DA outperforms other methods on the basis of higher throughput.

Table 3. Tabular comparison for lifetime

Protocol	Number of round when node is dead
	(FND) 1st	10th	(HND) 50th	90th	(LND) 100th
DEEC	1212	1375	1646	2383	2484
DEEC-DA	1422	1592	1919	2356	2534
DL-DEEC with DA	1285	1896	2004	3904	NO LND
DL-DEEC without DA	1242	1797	1945	3433	NO LND
DEEC-DA WRT DEEC	17.33%	15.78%	16.59%	-1.13%	2.01%
DL-DEEC with DA WRT DEEC	6.02%	37.89%	21.75%	63.83%	NA
DL-DEEC without DA WRT DEEC	2.48%	30.69%	18.17%	44.06%	NA

Stable period and overall lifetime are increased significantly

In DEEC the number of rounds when node is dead (FND): 1212 (1st round), 1375 (10th round), 1646 (50th round), 2383 (90th round), 2484 (100th round).whereas DEEC-DA number of rounds when node is dead (FND): 1422 (1st round), 1592 (10th round), 1919 (50th round), 2356 (90th round), 2534 (100th round).Further DL-DEEC with DA Number of rounds when node is dead (FND): 1285 (1st round), 1896 (10th round), 2004 (50th round), 3904 (90th round), No LND (100th round),DL-DEEC without DA Number of rounds when node is dead (FND): 1242 (1st round), 1797 (10th round), 1945 (50th round), 3433 (90th round).

Comparison between DEEC-DA and DEEC: DEEC-DA WRT DEEC: The percentage difference in the number of rounds when the node is dead compared to DEEC.

1st round: 17.33% more, 10th round: 15.78% more, 50th round: 16.59% more, 90th round: -1.13% (less), 100th round: 2.01% more.

Comparison between DL-DEEC with DA and DEEC: DL-DEEC with DA WRT DEEC: The percentage difference in the number of rounds when the node is dead compared to DEEC.

1st round: 6.02% more, 10th round: 37.89% more, 50th round: 21.75% more, 90th round: 63.83% more, NA (100th round).

Comparison between DL-DEEC without DA and DEEC: DL-DEEC without DA WRT DEEC: The percentage difference in the number of rounds when the node is dead compared to DEEC.

1st round: 2.48% more, 10th round: 30.69% more, 50th round: 18.17% more, 90th round: 44.06% more, NA (100th round)

Table 4. Tabular comparison for throughput

Protocol	Number of round when node is dead
	(FND) 1st	10th	(HND) 50th	90th	(LND) 100th
DEEC	9280	10982	12423	13660	13665
DEEC-DA	12363	13372	14606	15067	15078
DL-DEEC with DA	12682	18199	18828	21880	21926
DL-DEEC without DA	12277	17342	18240	20560	21020
DEEC DA WRT DEEC	33.22	21.76	17.57	10.30	10.34
DL-DEEC with DA WRT DEEC	36.66	65.72	51.56	60.18	60.45
DL-DEEC without DA WRT DEEC	32.30	57.91	46.82	50.51	53.82

In the Table 4, the number of rounds when a node is dead (FND) for DEEC, DEEC-DA, DL-DEEC with DA, and DL-DEEC without DA are presented for different rounds, including 1st, 10th, HND (half of network dead), 50th, 90th, and LND (all nodes in the network dead).

For DEEC, the FND ranges from 9280 in the 1st round to 13665 in the 100th round. In DEEC-DA, the FND ranges from 12363 in the 1st round to 15078 in the 100th round. In DL-DEEC with DA, the FND ranges from 12682 in the 1st round to 21926 at LND. In DL-DEEC without DA, the FND ranges from 12277 in the 1st round to 21020 at LND.

In terms of percentage change, DEEC-DA shows a 33.22% increase in FND compared to DEEC in the 1st round and a 10.34% increase at LND. DL-DEEC with DA shows a 36.66% increase in FND compared to DEEC in the 1st round and a 60.45% increase at LND. DL-DEEC without DA shows a 32.30% increase in FND compared to DEEC in the 1st round and a 53.82% increase at LND.

The results suggest that adding DA (dynamic clustering) to DEEC can improve network lifetime by delaying node deaths, particularly at later rounds. DL-DEEC with DA performs better than both DEEC and DL-DEEC without DA in terms of FND at all rounds.

Table 5. Tabular comparison for average residual energy

Protocol	Number of round when node is dead
	(FND) 1st	10th	(HND) 50th	90th
DEEC	0.191	0.130	0.058	0.000
DEEC-DA	0.179	0.118	0.035	0.002
DL-DEEC with DA	0.298	0.149	0.043	0.003
DL-DEEC without DA	0.291	0.081	0.038	0.006

For FND, HND, LND the amount of average residual energy remains approximately same.

But number of rounds are increased in DEEC-DA and in DL-DEEC hence energy optimization is achieved

The provided data represents the performance of different protocols, including DEEC, DEEC-DA, DL-DEEC with DA, and DL-DEEC without DA, based on the fraction of the network nodes that are considered dead (FND) at different rounds.

For DEEC, the FND values are 0.191 (1st round), 0.130 (10th round), 0.058 (HND - half of network dead), and 0.000 (50th and 90th round). This indicates that in DEEC, a fraction of 19.1% of nodes are dead in the 1st round, which decreases to 0% by the 50th and 90th round.

In DEEC-DA, the FND values are 0.179 (1st round), 0.118 (10th round), 0.035 (HND), and 0.002 (50th and 90th round). The results show a slightly lower fraction of dead nodes compared to DEEC at all rounds.

DL-DEEC with DA performs even better, with FND values of 0.298 (1st round), 0.149 (10th round), 0.043 (HND), and 0.003 (50th and 90th round). This indicates a significant improvement in terms of network survival, as a smaller fraction of nodes are considered dead in each round.

DL-DEEC without DA also shows promising results, with FND values of 0.291 (1st round), 0.081 (10th round), 0.038 (HND), and 0.006 (50th and 90th round). This protocol performs slightly better than DEEC in terms of reducing the fraction of dead nodes.

In summary, both DEEC-DA and DL-DEEC (with and without DA) demonstrate improvements over the standard DEEC protocol in terms of network lifetime. DL-DEEC with DA shows the highest performance, achieving the lowest fraction of dead nodes at each round, followed by DL-DEEC without DA and DEEC-DA.

The comparison of network lifetime across different protocols, as depicted in Table 3, highlights notable improvements achieved through the integration of dynamic clustering and data aggregation mechanisms in wireless sensor networks (WSNs). Specifically, the DEEC-DA and DL-DEEC with DA protocols demonstrate enhanced stability and prolonged network longevity compared to the baseline DEEC protocol. For instance, DEEC-DA exhibits a consistent increase in the number of rounds before node death (FND) across various rounds, indicating its effectiveness in prolonging network lifetime. Similarly, DL-DEEC with DA showcases remarkable improvements in FND, particularly evident in later rounds, suggesting its robustness in sustaining network operations over extended durations.

These findings hold significant implications for the broader field of WSNs, particularly in the context of enhancing network reliability, scalability, and resilience. By leveraging dynamic clustering and data aggregation techniques, such as those employed in DEEC-DA and DL-DEEC with DA, WSNs can better adapt to dynamic environmental conditions, mitigate network failures, and optimize resource utilization. Furthermore, the observed improvements in network lifetime underscore the potential of these advanced protocols to support mission-critical applications requiring continuous and reliable data transmission over prolonged periods.

Moreover, the comparison of average residual energy presented in Table 5 further elucidates the energy-efficiency benefits conferred by the proposed protocols. Despite the increased number of rounds, both DEEC-DA and DL-DEEC with DA demonstrate superior energy optimization compared to the baseline DEEC protocol, as evidenced by lower average residual energy values. This indicates that the integration of dynamic clustering and data aggregation not only enhances network lifetime but also contributes to more efficient energy utilization, thereby prolonging the operational lifespan of WSNs while minimizing resource depletion.

The findings from this comparative analysis highlight the transformative potential of advanced optimization techniques, such as dynamic clustering and data aggregation, in shaping the future of WSNs. By improving network stability, longevity, and energy efficiency, protocols like DEEC-DA and DL-DEEC with DA pave the way for the development of robust and resilient WSNs capable of supporting diverse applications across domains, including environmental monitoring, industrial automation, and smart infrastructure management.

The observed improvements in network lifetime and energy efficiency showcased by protocols like DEEC-DA and DL-DEEC with DA have significant implications for both future research and practical deployments in wireless sensor networks (WSNs). In terms of research, these findings point towards avenues for algorithmic refinement, including finetuning protocols for better performance and exploring adaptive mechanisms to dynamically adjust network parameters. Integration with emerging technologies such as AI and machine learning also holds promise. For practical deployments, DEEC-DA and DL-DEEC with DA offer opportunities to enhance real-world applications across industries like agriculture, environmental monitoring, and healthcare, optimizing infrastructure and contributing to resilient IoT ecosystems.

The results presented in the analysis of clustering protocols in wireless sensor networks offer valuable insights that can influence future research directions and practical applications in several ways:

• •    Enhanced Energy Efficiency: The comparative analysis of average energy consumption across different clustering protocols highlights the importance of energy-efficient strategies in prolonging network lifetime. Future research could delve deeper into the development of innovative energy-saving techniques, such as advanced data aggregation algorithms or optimized routing protocols, to further enhance energy efficiency in wireless sensor networks. Practical applications could benefit from these advancements by achieving longer operational lifetimes and reduced maintenance costs.

• •    Improved Network Sustainability: The evaluation of network lifetime and the number of dead nodes provides crucial information about the sustainability of clustering protocols. By identifying protocols that exhibit higher network longevity and lower node failure rates, future research can focus on refining these protocols or developing new methodologies to enhance network sustainability. Practical applications, especially those involving long-term monitoring or deployment in remote areas, stand to gain from more robust and resilient network infrastructures.

• •    Optimized Data Transmission Rates: The analysis of throughput underscores the importance of efficient data transmission mechanisms in wireless sensor networks. Future research efforts could explore novel approaches to

further optimize data transmission rates, such as adaptive modulation techniques or dynamic channel allocation schemes. Practical applications requiring real-time data delivery or high-throughput communication, such as industrial automation or disaster response systems, could benefit significantly from these advancements.

• •    Energy Optimization Strategies: The comparison of average residual energy levels offers valuable insights into energy optimization strategies within clustering protocols. Future research could focus on developing intelligent algorithms or machine learning techniques to dynamically adjust node behavior based on energy levels and network conditions. Practical applications could leverage these energy optimization strategies to achieve better resource utilization and mitigate the impact of energy constraints on network performance.

• •    Interdisciplinary Collaborations: The multifaceted nature of wireless sensor networks necessitates interdisciplinary collaborations between researchers from various domains, including computer science, engineering, and mathematics. Future research endeavors could foster interdisciplinary collaborations to address complex challenges in wireless sensor networks comprehensively. Practical applications could benefit from holistic solutions that integrate expertise from diverse fields to tackle real-world problems effectively.

Potential limitations or challenges in implementing the proposed approach in real-world scenarios could include:

• •    Computational Complexity: The utilization of optimization algorithms like PSO-GSA and fuzzy logic for data aggregation may introduce computational overhead, requiring substantial processing power and memory resources on sensor nodes, which could be a challenge in resource-constrained environments.

• •    Algorithm Tuning and Calibration: Fine-tuning parameters and calibrating the PSO-GSA algorithm and fuzzy logic system for different deployment scenarios and environmental conditions may be non-trivial tasks, requiring expertise and effort.

• •    Sensitivity to Environmental Dynamics: The effectiveness of the proposed approach may be sensitive to dynamic changes in the wireless environment, such as variations in signal interference, node mobility, and environmental conditions, which could affect the reliability and robustness of CH selection and data aggregation.

• •    Integration Complexity: Integrating the proposed hybrid approach into existing WSN infrastructures or deployment frameworks may pose challenges in compatibility, interoperability, and seamless integration with other network components and protocols.

• •    Practical Deployment Considerations: Real-world deployment of the proposed approach may require careful planning, including node placement, network configuration, and maintenance procedures, to ensure optimal performance and longevity, which could be time-consuming and resource-intensive.

• •    Validation and Testing: Conducting extensive field trials and validation experiments in diverse real-world environments to assess the scalability, reliability, and effectiveness of the proposed approach may be challenging and resource-demanding.

6.    Conclusions

Addressing these limitations and challenges would require comprehensive validation studies, optimization of algorithm parameters, robustness testing, and careful consideration of practical deployment factors to ensure the successful implementation and adoption of the proposed approach in real-world WSN deployments.

This paper offers an innovative approach to select cluster heads within the framework of the DEEC algorithm. Our proposed PSO-GSA approach combines the PSO and GSA to enhance the CH selection process, taking into account both energy efficiency and network coverage in a wireless sensor network context. The integration of PSO and GSA capitalizes on the unique strengths of each algorithm, resulting in more optimal CH selection and enhanced performance of the DEEC algorithm.

Moreover, we introduce the application of fuzzy logic for data aggregation, which significantly improves the accuracy and efficiency of sensor data aggregation in the WSN. By incorporating the residual energy and transmission distance as input parameters into the fuzzy logic system, we can effectively determine the data aggregation weights for the primary and secondary cluster heads. This approach facilitates the efficient utilization of available energy resources and overall enhancement of the WSN performance.

The proposed hybrid approach, combining PSO-GSA for CH selection and fuzzy logic for data aggregation, represents a unique and original contribution to the field of WSNs and optimization techniques. It addresses the challenges of energy efficiency and network coverage in CH selection while improving the accuracy and efficiency of data aggregation. Through extensive simulations and analysis, we have demonstrated the effectiveness and superiority of our proposed approach over existing methods.

Our research not only enhances the performance of the DEEC algorithm but also contributes to the advancement of WSNs by proposing a hybrid approach that combines optimization algorithms and fuzzy logic. This work opens up opportunities for further exploration and development of advanced techniques in WSNs, providing a foundation for more energy-efficient and robust sensor network deployments in various real-world applications.