A Hybrid Restoration Approach of Defocused Image Using MGAM and Inverse Filtering

Shooting a real world image with a camera, at least some parts are affected by a blur and noise. Atmospheric turbulence, longer exposures, and so on can blur images, but the exact cause of blurring may be unknown. Restoration in the case of known blur, assuming the linear degradation model, is called linear image restoration and it has been presented extensively in the last three decades giving rise to a variety of solutions [1–3]. In many practical situations, however, the blur is unknown. Hence, both blur identification and image restoration must be performed from the degraded image. Restoration in the case of unknown blur is called blind image restoration [4, 5]. Existing blind restoration methods can be categorized into two main groups: (i)

those which estimate the PSF a priori independent of the true image so as to use it later with one of the linear image restoration methods, such as zero sheet separation, generalized cross validation, and maximum likelihood and expectation maximization based on the ARMA image model [6, 7], and (ii) those which estimate the PSF and the true image simultaneously, such as nonnegative sand support constraints recursive inverse filtering, maximum likelihood and conjugate gradient minimization, and simulated annealing [8,  9].

Algorithms belonging to the first class   are computationally simple, but they are limited to situations in which the PSF has a special form, and the true image has certain features. The investigated defocused image restoration algorithms by using local polynomial nonparametric regression method belongs to the second class, which are computationally more complex, then it must be used for more general situations. In this paper, a kind of semi-blind image restoration algorithm is proposed in case of known the blur type (defocused blurring) with bivariate generalized nonparametric statistical regression additive model of no curse of dimensionality and good local kernel smoothing technique and classical image restoration method inverse filtering.

In general, discrete bivariate digital image model for a linear degradation caused by blurring and additive normal white noise with mean 0 can be given by the following equation

y (i, j) = h (i, j) * f (i, j) + n (i, j),              (1)

where       *       indicates       two-dimensional convolution, f(i, j) represents on original image, y(i, j) is the degraded image, h(i, j) represents the two-dimensional PSF , and n(i, j) is the additive noise. As for defocus blur, PSF is modeled as a uniform intensity distribution within a circular disk,

h(i, j) = 5 n RR

if 7 i2 + j2 < R otherwise

（ 2 ）

where disk radius R is the only unknown parameter for this type of blur.

Fourier methods can be used to estimate the defocus parameter R through calculating a ratio of power of high frequencies portion to that of low frequencies portion. However, a main drawback of the method is its bad noise immunity. To solve this problem, literature [11] has proposed a novel algorithm to overcome this shortcoming, the RBF neural network is applied to fitR . This scheme has good fitting, but bad prediction. To avoid the weak generalization ability, a more efficient method for estimating parameter R is proposed in this paper. The prediction ability of these two methods is compared with the trained five images. The steps of the presented algorithm in this paper is as follows: Firstly we construct feature vectors of several blurred images with known defocus radius R in wavelet domain of defocused digital image, then a multivariate generalized additive model (MGAM) [12-15] with nonparametric local kernel technique [16-19] is trained using the vector s as inputs and defocused parameters as outputs. After the model is trained, the new defocused images are applied to the trained model for predicting the parameter R . In this paper, inverse filtering (InvF) [4, 20] is adopted to image restoration.

Here the features in wavelet domain of defocused diagonal directions respectively. Decomposition into l levels of an original image results in a down sampled image of resolution 2l with respect to the image as well as detail images. In order to denote the relationship between wavelet coefficients and defocused radius R , we define five variables named v , v , v , v , and v as:

' V 1=\V2 I s/IH2 I s ,

V2 =IH2 Is/IX2 Is ,

* V3 = IH11s /num{H1}, v4 = H 2I s/num{H 2}, _v5 = ID11s /num{D1} where | • | s represents the summation of all coefficients’ absolute value, num {•} is total number of coefficients.

An original image is blurred artificially by a uniform defocused point spread function   (PSF)  with parameter R whose value ranging from 1 to 20. The relationships between v , v , v , v , v andR are shown in Fig.1, where the curves are normalized in [0, 1] interval. When R increases, v , v , v and v decrease monotonously.

digital image are discussed. The l level wavelet decomposition of the defocused digital image I results in an approximation image X and three detailed images H , V , and D in horizontal, vertical, and

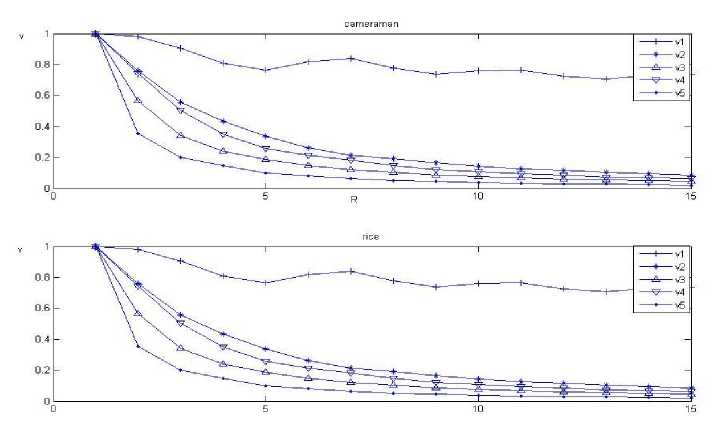
Figure 1.Relationship between v    and R

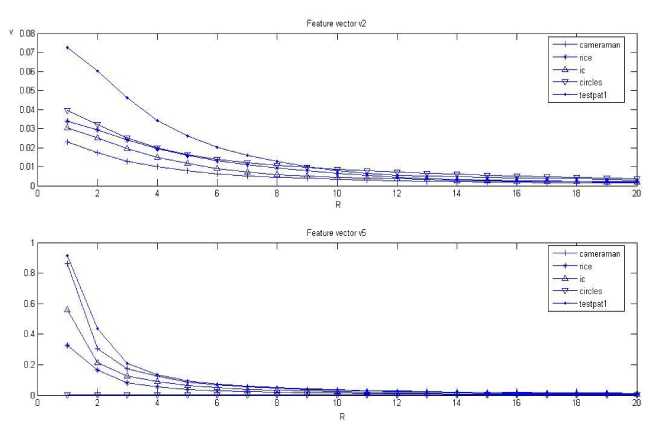
Figure 2.Curve v , and v of Different Images

In order to estimate defocus parameter R , only known the roughly similar relationship is not enough. As shown in Fig. 2, every image has monotonous curve between v , v and R , but they are not superposition. For a degraded unknown PSF image, R cannot be calculated because the curve of the given image is not known. For example, if v of image ”rice” has been calculated, and then we estimate R according curve if ”ic” in Fig. 2, wrong results are obtained obviously. To solve this problem, one of the methods is to choose neural networks. Computational artificial neural networks are known to have the capability for performing complex mappings between input and output data, but neural network method has bad generalization ability. Here we propose a MGAM to estimate R by using the variables v .

II TRAINING MULTIVARIATE GENERALIZED ADDITIVE MODE

Multivariate local polynomial model is an attractive method both from theoretical and practical point of view. In this kind of multiple linear regression model, although generalizations of most of the univariate smoothing techniques to multivariate surface smoothing appear to be feasible, there is a serious problem arising: the so-called curse of dimensionality. Because of the curse of dimensionality, surface smoothing techniques are in practice not very useful when there are more than two or three predictor variables. MGAM is one of good multivariate dimensionality reduction techniques. In this Section, we briefly outline and review the idea of the extension of MGAM to the defocused parameter.

Suppose that the input vector is V = (v, v2, v3, v4, v5 ). The model is fitted by the function R = m(V) .

Our purpose is to obtain the estimation RR = m(V) of function m . This paper, we use the generalized additive model function  m(V)  to predict the defocused parameter R value based on the point V of the test image.

Consider the general multiple regression model

R = m (V ) + 8 ,                             ( 4 )

where E ( e ) = 0 ; Var ( e ) = 6 Г ² and 8 is independent of the vector of covariates V . In linear multiple regression model the regression function m ( • ) is assumed to be linear and hence additive in the predictors. In additive models the linearity assumption is dropped and the additive feature is retained, leading to the following model

^R = ^{a +} Z d j = 1 ^fj ⁽ V j ) ^{+ 8 ,}                ( 5 )

where    f1, f2,   , fd are unknown univariate functions.

The additive model (5) generalizes the linear multiple regression model with the linear function replaced by an additive sum of univariate functions. The additive model can be generalized to a generalized additive model which links the mean regression function to an additive sum of univariate funcitons:

f (m(V))=a+X^d=1 gj(vj) , where f (•) is a known link function and f , f ,   , f are unknown univariate functions.

We start with describing the algorithm for fitting a parametric generalized linear model with canonical link function f :

f {m(V )}= V в = ^V).

Twenty original images are chosen to train the model which can be given the good relationship between them. The defocused parameter R based on the digital image is the model output. The images are defocused artificially with R whose value ranging from 2 to 7. So the total numbers of training samples are 120. Then feature vectors are constructed using variables v of each image:

V = (Vi, V2, V3, V4, V5).

• III    INVERSE FILTERING

In this section, we introduce the inverse filtering approaches to image restoration that utilize minimum mean square error as an optimization criterion. The image degradation process is often represented in terms of a matrix-vector formulation of Equation (1). This is given by y = Hf + n , where y , f , and n are the observed, original, and noise images, ordered lexicographically by stacking either the rows or the columns of each image into a vector. When utilizing the stationary model, H becomes a block-Toeplitz matrix representing the linear convolution operator h ( i , j ) . Toeplitz, and block-Toeplitz matrices have special ”banded” properties which make their use desirable for representing linear space-invariant operators. By padding y and f appropriately with zeros so that the results of linear and circular convolution are the same, H becomes a block circulant matrix. This special matrix structure has the form

H = ' H(0) H(1) H (N — 1)  • H(0) H (1) " H(2) ,     (6) V H ( N — 1) H (N — 2)  • •  H (0) v where each sub-matrix H(i) is itself a circulant matrix.

Notice that each block-row of H and each row of H(i)) is a circular shift of the prior block-row or row, respectively. Classical direct approaches to solving Equation (1) have dealt with finding an estimate f which minimizes the norm y — Hfˆ , thus providing a least squares fit to the data. This leads directly to the generalized inverse filtering, which is given by the solution to (HTH) f = HTy .

The critical issue that arises in this approach is that noise amplification. This is due to the fact that spectral properties of the noise are not taken into account. In order to examine this, consider the case when H (and, therefore, H^T ) is block circulant, as described above. Such matrices can be diagonalized with the use of 2-D Discrete Fourier Transform ( DFT ). This is because the eigenvalues of a block circulant matrix are the 2-D discrete Fourier coefficients of the impulse response of the degradation system which is used in uniquely defining H , and the eigenvectors are the complex exponential basis of this transform. In matrix form, this relationship can be expressed by

H = WhW - 1 ,                          ( 7 )

where h is a diagonal matrix comprising the 2-D DFT coefficients of h ( i , j ) , and W - ¹ is a matrix containing the components of the complex exponential basis functions of the 2-D DFT . Pre-multiplication of both sides of Equation(7) by W ^{— 1}, the solution can be written in the discrete frequency domain as F ( to ) = h ( to ) Y ( to )/ | h ( to ) |² , where F ( to ) ; h ( to ) , and Y ( to ) denote the DFT of the restored image, f ˆ( i , j ) , the PSF , h ( i , j ) , and the observed image, y ( i , j ) , as a function of 2-D discrete frequency index to , where to = ( k, , k ₂ ) for k = 0,1,-, M — 1 , k ₂ = 0,1,-, N — 1 , for an M x N point DFT , and * denotes complex conjugate.

• IV    SIMULATION RESULTS

The performance of the proposed image restoration algorithm based on multivariate generalized additive model and inverse filtering has been evaluated using the classical gray-scale Moon image, Coins image, Saturn image, and Cameraman image in Matlab toolbox, and one real blurred image is used for the deconvolution procedure. The results show our method is very successful for the restoration based on this kind of blurred image. In image restoration studies, the degradation modelled by blurring and additive noise is referred to in terms of the metric blurred signal-to-noise ratio (BSNR) . This metric for a zero-mean M x N image is given by

BSNR = 10log 0<

— У^У"^ 2( m, n) , MN ^m=1 ^n=1

（8）

where z ( m , n ) is the noise free blurred image and (7 2 is the additive noise variance. For the purpose of objectively testing the performance of linear image restoration algorithms, the improvement in signal-to-noise ratio (ISNR) is often used. ISNR is defined as

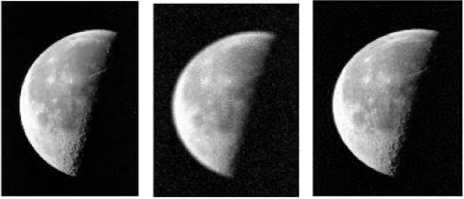
Figure.3. True image (left); blurred image (middle); estimated image (right),BSNR=12.33, ISNR=22.51

ISNR = 10log10

fE M=i E N=i[ f(m,n) - y(m,n)]2 Ie M=1 e N=1[ f(m, n) - f(m, n)]2,

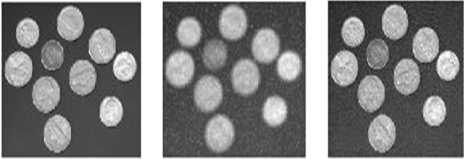
Figure 4.True image (left); blurred image (middle); estimated image (right).BSNR=11.21, ISNR=23.12

where f ( m , n ) and y ( m , n ) are the original and degraded image pixel intensity values and f ( m , n ) is the restored true image pixel intensity value. ISNR cannot be used when the true image is unknown, but it can be used to compare different methods in simulations when the true image is known.

In order to find good performances of the proposed multivariate generalized additive model ( MGAM ) and inverse filtering compared with the RBF neural network algorithm (RBFNN) for defocused digital image restoration which is investigated in the literature [11], the same defocused blurred images are used for the experiments. Mean squared prediction errors are shown in Table 1. From Table 1, we can conclude that the prediction results of MGAM predictor are significantly better than the RBFNN in the same simulated data.

Figs. 3, 4, 5 and 6, in which the true images, blurred images and estimated true images are depicted in the left, middle and right column, respectively, illustrate how the method behaves in Moon, Coins, Saturn and Cameraman digital images. It is Clear from Figs.3-6 that performances of the new novel digital defocused restoration method is effective in different images. Fig. 7 also shows that the presented algorithm is good for real blurred image.

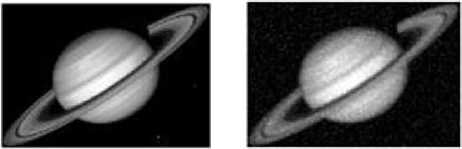
Figure 5.True image (left); blurred image (middle); estimated image (right).BSNR=13.15, ISNR=24.30

Figure.6. True image (left); blurred image (middle); estimated image (right).BSNR=11.53, ISNR=22.07

Table 1. MSE using both methods

trai nin g ima ge	method	eMSE	trainin g image	method	eMSE
Mo on	RBFNN	4.81 x 10 - 6	Coins	RBFN N	5.06 x 10 - 6
Mo on	MGAM	4.11 x 10 - 8	Coins	MGA M	3.95 x 10 - 8
Sat urn	RBFNN	6.62 x 10 - 6	Tire	RBFN N	8.04 x 10 - 6
Sat urn	MGAM	5.63 x 10 -	9 Tire	MGA M	7.17 x 10 - 8

Figure.7. Result for real blurred image. Blurred image (left); restored image (right)

V CONCLUSION

A new method that is based on multivariate

generalized additive model which is a nonparametric statistical method for good high-dimensional data and inverse filtering for semi-blind restoration of blurred noisy images was proposed in this paper. Defocused digital image parameter was estimated by a multivariate generalized additive model trained in wavelet domain of the defocused noisy digital image. The main advantages of the proposed technique are that it is not only robust to noise because wavelet transform has an excellent de-noising ability, but also effective to artificially defocused and real blurred image. Defocused image restoration is successfully realized by the inverse filtering, resulting in improved the image quality. The presented algorithm was justified via simulated and practical image. Defocused image parameter can be successfully estimated by using trained model with a hybrid restoration method by using multivariate generalized nonparametric statistical additive regression model and inverse filtering. Simulated and real defocused digital image restoration results show the proposed algorithm is reliable, effective, and robust for defocused blurred noisy image restoration. Future works can be done in many fields include super resolution reconstruction, digital image interpolation, non-uniform noise, and so on. Moreover, it can be extended to other fields such as information hiding and digital covert communications.

ACKNOWLEDGMENTS

This work was partly supported by Natural Science Foundation Projects of Chongqing CSTC of China (CSTC2010BB2310, CSTC2011jjA40033, CSTC2012jjA00037), Chongqing CMEC Foundations of China (KJ120829).