A Light-weight Symmetric Encryption Algorithm Based on Feistel Cryptosystem Structure

Published Online December 2014 in MECS DOI: 10.5815/ijcnis.2015.01.03

Wireless Sensor Networks(WSNs) is a kind of network which is composed of a lot of tiny wireless sensors with low cost, low power consumption and the environmentperception capability[1,2]. WSNs synthesize the sensor technology, embedded computing technology, and distributed information processing technology and wireless communication technology. WSNs can real-time monitor, perceive and deal with the information of monitored objects in some the areas, and transmit the monitoring information to the end-user through Selforganizing wireless communication networks and multistage-relay-transmission method. WSNs combine the logic information world with the real physical world, which changed the communication way of the people and the natural. The application prospect of WSNs is very wide. In the military filed, the WSNs can be used to realtime track of Battlefield targets[3,4]. In the environment monitoring filed, WSNs can be used for the collection of temperature, humidity, air pressure[5,6]. In the medical filed, WSNs can be used for patient care, remote medical care and others[7]. WSNs is also used to monitor the health condition of bridges, highways, skyscrapers[8,9]. As a result of the enormous application value of WSNs, it has become the one of the research hotspots in the current computer and communication science filed.

However, WSNs has faced a number of security threats. Because WSNs node is usually deployed in unattended wild environment, the wireless signal is easy to be interfered and intercepted, and the WSNs node also maybe stolen and damaged. So the security environment of WSNs is very poor. In addition, WSNs node is usually the tiny and cheap sensor which is powered by battery, and its battery capacity, CPU performance and RAM capacity are all very limited. Furthermore, WSNs sensors have many categories, and the protocols are not uniform. These problems make the existing, mature network security mechanism can not be directly used in WSNs. So, there exit a lot of WSNs security problems which are not solved, and the data encryption technology is one of the important security problems. Currently, many scholars have done a lot of researches about the data encryption technology of WSNs.

On the basis of the Feistel Cryptosystem Structure, the paper proposed a new light-weight symmetrical encryption algorithm, named LESEA. It adopts minor encryption rounds, short data packet, and simplified scrambling function S, which can greatly reduce the cost of the encryption and decryption. At the same time, LESEA use the longer bits Key and circular interpolation algorithm to produce Child-Key, which ensures the security of the LWSEA algorithm without too much decline. Experiments demonstrate, the LWSEA algorithm has good “avalanche effect” and data chaos, the security performance is better. Its calculation speed is faster than the standard DES algorithm, and has lower cost. These excellent features make LWSEA algorithm more suitable for the resources-restrained WSNS than DES and other symmetrical encryption algorithms. LWSEA algorithm can greatly improve the work efficiency and survival time of WSNs node, which has an important contribution to promote the wide application of WSNs.

The section 2 and 3 study the main characteristics and the security requirements of WSNs, which establish the research foundation for designing a new encryption algorithm. Section 4 analyzes the feature of the Feistel Cryptosystem Structure, which looks for accurate designing direction for new algorithm that is suitable for WSNs encryption. Section 5 and 6 puts forward the detailed content of a kind of light-weight symmetrical encryption algorithm. Section 7 tests the performance of LWSWA algorithm with experimental program and the TS1 wireless sensor produced by ISI Corporation, and compared LWSWA algorithm with the standard DES encryption algorithm, which is concluded the ideal experiment results.

• II.    Related Works

There are many scholars have detailed research the problem of data encryption in WSNs[10-14]. Vivaksha Jariwala[15] attempt at evaluating the performance of various privacy homomorphism algorithms in WSNs. Their creative achievement is to identify homomorphic encryption algorithm for WSNs that offers security at the minimum overhead. Tong XiaoJun et al [16] proposed a block encryption scheme based on hybrid chaotic maps dynamically and an integer digital random method with the Feistel network structure, which is a kind of fast, secure, and suited for WSNS data encryption, but the cost of the scheme, is closed to DES algorithm. Zhao Yongan[17] proposed an encryption scheme supporting secure  in-net-work processing for wireless sensor networks based on learning the existing security schemes. Du Dahai[18] proposed a key management scheme based on EBS, it can refresh the keys in WSNs securely and efficiently, the scheme enhances network security while conservatively consuming nodes. Zhang Ruiqing[19] measured the energy cost of some security decryption algorithms in WSNs, and gives some guidelines for the application of decryption algorithms in WSNS. Claude castelluccia [20] blend inexpensive encryption techniques with simple aggregation methods to achieve very efficient aggregation of encrypted data, and extend the proposed scheme to provide end-to-end aggregate authentication, which is provably secure against outsider-only attacks. But the scheme increases the burden of gateway node. Domingo et al [21] propose first approach for symmetric homomorphic encryption function. The approach works on message-part, after making partition of original message. Claude Castelluccia et al [22], proposed an algorithm based on a modular addition that is very well suited for CPU constrained devices. S. Peter [23] proposed an approach for symmetric privacy homomorphism that takes advantage of both [21] and [22] and proposed a combined cryptosystem. In paper[24], author proposed a probabilistic additive asymmetric algorithm, and consider that none of these evaluations are aimed at the resource constrained WSNs. Levent et al [25] implement DF[21] scheme in WSNs, however the paper doesn’t aim at benchmarking the prevalent state-of-the-art homomorphic encryption algorithms in WSN environment.

• III.    Important Characteristic Of Wsns

We have studied many categories WSNs and collected some common characters of them. This is of great instructive significance to design new security architecture of WSNs. The common structure chart and characters are shown as follow respectively.

Data Process Center

Gateway Node 2

WSNs 2

WSNs 1

WSNs 3

Wireless Channel

Gateway Node 1

Wireless base station

Gateway Node 3

Fig. 1: Common structure chart of WSNs

• •    Resource-restrained sensor . As the majority of WSNs sensor are tiny volume, use built-in battery to provide power, and adopt embed CPU and RAM, its electronic power, calculation ability and the storage capacity is very limited.

• •    Limited communication ability . WSNs sensor’s bandwidth is narrow and the power is so low, its communication coverage area is usually only tens to hundreds of meters. The WSNs sensors sometimes deployed to the mountains, skyscrapers, bridges and other complex landform area, so that the connectivity of the network will be greatly affected.

• •    Difficult maintain of network topology . WSNs node is of great number and widely dispersed. Constantly the new node joins or an old node failure (power runs out or sensor damaged), and communication links are easily interrupted for the effect of complex landform. These cases will result in frequent changes of network topology; furthermore, result in relatively expensive maintenance-cost in data communication and routing construction

• •    High data flux . Unlike the way of the Internet which uses IP addressing, the WSNs node use private identifier to addressing. WSNs node monitor specific events and data according to presetting instructions. Each WSNs node is usually create larger streaming data, and transmit to the gateway node in real time.

• •    Application relativity . WSNs have a wide range of applications. But for the needs of different application, WSNs node’s function and working environment will be of great difference. These features make many traditional network security technology can’t be applied to WSNs.

Iv. Information Security Requirement Of Wsns

Opening deployment and wireless broadcast characteristics of WSNs determine the existence of latent security danger. So the WSNs and traditional networks have same security requirements. Although there are some differences in security requirement to different application-background WSNs, they still have the common needs which are listed below.

• •    Confidentiality . Confidentiality is to request that the transmission of importance information between the WSNs node should be encrypted. Authorized users through a specific key to encrypt and decrypt information, non-authorized users can not get the correct data because of no key.

• •    Integrity . The packets received by WSNs node can not be malicious inserted, deleted and tampered.

• •    Robustness . Even if part of the network is attacked, it will not lead to paralysis of the whole WSNs.

• •    Access Control . Identity of all WSNs nodes can be mutual authenticated. Thus, only legal users can access the service and resource of WSNs.

• • Non-repudiation . WSNs node can not deny its

behavior of sending data packet.

• •    Authenticity . WSNs can verify the authenticity of the source data packets, thus it is impossible for attacker to masquerade as a legal node without be found.

• V. Feistel Cryptosystem Structure

The cryptographer, Horst Feistel invented Feistel Cryptosystem Structure when he researched Lucifer group password. The structure is used to DES , a famous symmetrical encryption algorithm. There are many group-encryption algorithm also adopted Feistel Cryptosystem Structure, such as DES, BLOWFISH, RCS and so on. Feistel Cryptosystem Structure is the typical iteration encryption algorithm; its work process is listed below.

Encryption process of Feistel cryptosystem algorithm is shown as followed

• 1)    Given the total length of 64-bit plaintext U = LP i RP i . Here LP i is the left 32-bit of U, and RP i is the right-32bit of U.

• 2)    Using the following formula to do 16 times identical iterative computation.

LP i = RP - 1

RP = LP i - i © E ( RP i - i , K i ) i = 1,2,3,.....,16

In the formula 1, the E is the rounds-function, used for encrypt data packets. K i =K 1 ,K 2 , . . . K 16 are the child-Key, which are generated by seed-Key K . ○ + is the XOR operator.

• 3)    To exchange the LP 16 and RP 16 when the last iterative computation is finished, then a cipher text V = RP ₁₆ LP ₁₆ is produced.

Decryption process of Feistel cryptosystem algorithm is shown as follow

• 1)    To do the cipher text V as the following conversion: LC_{i -1}= RP _16-i+1, RC_{i -1}= LP _16-i+1, i = 1, 2...16,17

• 2)    Using the following formula to do 16 times identical iterative computation.

LC = RC^

RC i = LC i — 1 © E ( RC — 1 , К . )         ⁽²⁾

i = 1,2,3,.....,16

After the iterative computation is completed, the cipher text V can be restored to the plaintext U.

What can be learnt from the formula 1 and 2 is that the encryption process and the decryption process of the Feistel cryptosystem are the same, but the applying sequences of child-Keys are just opposite. The applying sequences in encryption is K 1 , K 2 ,... K 16 , while in decryption is K ₁₆, K ₁₅ ... K ₁. This structure can ensure the reversibility of encryption process, so the encryption and the decryption can share a cryptosystem algorithm, the similar rule can also be applied to the encryption Key and the decryption Key. Seeing from the back experiment results, only using formula 1 to do 16 times iterative computation can get highly intensive encryption effect. The advantages of the algorithms based on Feistel Cryptosystem Structure are simple, easy to use, low cost, and low requirements to computer system, which are more suitable for the security needs of resource-restrained of WSNs node. In the paper, basing on Feistel Cryptosystem Structure, we proposed a new symmetrical cryptosystem that possess lower calculation cost and system requirements, but is nearly equal to the security level of DES.

• VI.    The Design Of Light-Weight Symmetrical Encryption Algorithm

Through the analysis of Feistel Cryptosystem Structure, we found that the encryption process is to initially arrange the plaintext with the scrambling table, and then making use of expand scrambling table to do further scrambling arrangement, finally, using the round-function E to do 16 rounds encryption operation to get the ultimate ciphertext. The decryption process is first to use inverse initial scrambling table and same expand scrambling table to do preliminary process for ciphertext, and then using round-function E to do 16 rounds decryption operation, the ciphertext will be restored into the original plaintext. The encryption process also introduced 8 S -box functions to assisting scramble intermediate results of encryption, which make the ciphertext is more disorder and chaos, and improve the security level of the ciphertext. But this method increased the burden of computer system, and it is not suited for WSNs nodes whose computing ability, RAM capacity and battery power are very limited.

In fact, if round-function E is a pseudo-random function which use cryptographic key K as seed. Using E to do four rounds operation for the plaintext can make encrypted data take on pseudo-random permutation. If execute 5 rounds operation, it is enough to make encrypted data become a “strong” pseudo-random permutation. Therefore, if the requirement of security intensity is not very high, but high encryption speed and low cost is required, it is not necessary to make use of 16 rounds encryption operation for Feistel Cryptosystem.

Resources in most WSNs nodes, such as CPU performance, memory capacity and battery power are extremely limited. In some occasions, encryption algorithm needs to run at tremendous speed so that the data can be processed in real time. This kind of node can only use the encryption algorithm that is simple, takes up fewer resources and calculate rapidly. We have proposed the following improvement measurements after analyzing the Feistel Cryptosystem Structure: Simplify the structure of the round-function E ; reduce the encryption times of the round-function E and the quantity of child-key, but increase the length of the encryption-key K; design new S -box function to enhance encryption effects. This new kind of symmetry encryption algorithm is called LWSEA whose concrete design methods are shown as follows.

• A.    The encryption procedure of LWSEA algorithm

LWSEA algorithm adopts the encryption-key K with 120 bit, which is greater than the DES algorithm of 56 bit. The encryption child-key makes use of six keys, namely K i ~ K 6 .The length of each child-key is up to 36 bit. The child-key K i is vital to the security level of LWSEA algorithm. So the generation method of child-key is the pivotal factor. Firstly, we do a linear displacement for encryption-key K , which can disorganize the bit-array of K , and the displacement result is named M 0 . Through the displacement table is a big matrix (12×10), the paper isn’t able to show it. M 0 left-cyclic shift 48 bits, the result is record as M 1 , and then M 0 right-cyclic shift 48 bits, the result is record as M 2 . The M 0 , M 1 , M 2 are named seed keys, and their length are all 120 bits. Based on M 0 , M 1 , M ₂, LWSEA will generate six original Keys, named N ₁, N ₂, N ₃, N ₄, N ₅, N ₆, their length are all 120 bits. The generation method is shown as following formula.

N = M_ © [ S hift L ₆( M, ) © S hift R ₆( M ₂)] N ₂ = N 1 © [ S hift L ₃₂ ( M 0 ) © S hift R ₃₂ ( M ₂ )] N = N © [ S hift L ₄₈( M, ) © S hift R ₄₈( M ₂)] N = N © N © N

N 5 = N 4 © [ S hift L ₆₄ ( M ₂ ) © S hift R ₆₄ ( M 1 )] N = N © [ S hift L_{8 o}( M_x ) © S hift R ₆₄( M _o)]

The ShiftL16(M1) in formula 6 denote that make M1 left-cyclic shift 48 bits, and the ShiftR16(M2) denote that M2 right-cyclic shift 48 bits. The meaning of other items in formula 6 is by analogy. Formula 6 raise the complex degree of child-key, which enhance the difficulty to attacker. LWSEA use a compression-displacement table, named CPE, to do compression and displacement calculation to N1, N2, N3, N4, N5, N6, and the results are ultimate child-key K1, K2, K3, K4, K5, K6, viz. Ki=CPE(Ni), 1≤i≤6. The length of Ki is 36 bits, and is far less than Ni, and the decreasing in length is caused by compression calculation. The content of CPE is shown as following table.

Table 1: Child-Key Displacement Position

29	52	128	46	32	23
36	19	39	62	75	89
116	13	102	42	67	93
121	99	68	52	7	16
26	71	3	21	123	82
15	56	86	30	1	59

Table 1 is a 6×6 matrix. Through the table, the original key N _i with 120-bit will be transformed as K _i with 36-bit, which is the “compress effect” that is similar to hash encryption. The effect can hide the generation-source of K i , which can highly raise the security level of LWSEA.

The total plaintext in the LWSEA algorithm is grouped according to the length of 48 bits and each group continues to divide into two parts: LP 0 and RP 0 , and each contain 24 bit. In the encryption procedure, the child-key K _i is used according to the sequence of K ₁, K ₂, K ₃, K ₄, K ₅, K 6 , whereas in decryption procedure, it is used in the opposite sequence. Before encryption calculation, the plaintext needs to do a linear displacement; thereby the original array of plaintext is disorganized, which can raise the security level of LWSEA, the displacement table is shown as follow.

Table 2: Plaintext Displacement Position

13	32	48	12	26	45	5	36
31	8	35	20	3	25	30	7
14	39	11	34	37	16	44	22
28	1	19	15	46	27	4	42
9	33	29	47	2	17	40	21
23	43	10	38	18	41	24	6

The number 13 in table II denote that the 13^th bit in plaintext move to first bit, other number in the table is also the same meaning. After displacement, using expanding displacement table EX expands the length of RP ₀ to 36 bits, the same length with K _i. Table EX is shown as follow.

Table 3: Expanding Displacement Position

24	1	2	3	6	5	23	18	13
6	19	6	7	8	9	16	14	22
8	9	10	11	12	13	2	17	19
15	13	14	24	16	17	6	20	24

In fact, table EX select 12 bits from RP 0 to expand itself, which make its length extend to 36 bit.

After the procedure of plaintext preprocessing and child-key generation is ended, the formal encryption calculation will start. LWSEA algorithm executes the same calculation in several rounds to complete the total encryption procedure. Due to space limitations, the paper only detailed describes the first rounds. Firstly, the child- key K1 do XOR calculation with expanded RP0 (the XOR calculation is that often said encryption calculation), and then make the result do XOR calculation with LP0, the calculation result is recorded as RP1. Secondly, three different S-box functions are used to do the compression scrambling operation for RP1, as well as the length of RP1 is also decrease to 24 bit. Lastly, RP0 is assigned to LP1, and then RP1 and LP1 and K2 become the input data of the next round encryption calculation.

To reduce the encryption cost of WSNs node, the encryption calculation only executes 6 rounds, less than the 16 rounds of DES algorithm. But the LWSEA adopt longer encryption Key (120bit), so its security level haven’t obvious decline.

The integrated calculation procedure of LWSEA algorithm is shown as below figure.

Plaintext Input (48bit)

Left data ;               ;               ; Right data

LP 0 (24bit)          k ₁          RP 0 (24bit)

+ E

LP 1 =RP 0           RP 1 =LP 0 ⊕ E(RP 0 , k 1 )

_{+           E}                   k 2

.. ..

..

LP 5 =RP 4           RP 5 =LP 4 ⊕ E(RP 4 , k 5 )

_{+           E}                   k 6

RP 6 =LP 5 ⊕ E(RP 5 , k 6 )         ^LP6^=RP5

Cihpertext =LP 6 RP 6

Fig. 2: Encryption procedure of LWSEA algorithm

• B.    The decryption procedure of LWSEA algorithm

The decryption is the inverse procedure of encryption. There isn’t essential difference for the two calculations but the using sequence of child-key K i . The output result in the encryption process is equivalent to the input result in the decryption process. Therefore, in the initial stage of decryption, there exists LC ₀ = RP ₆ and RC ₀ = LP ₆. By analogy, we can deduce the following formula.

LC  RP 6 - i

RP - i = LC 6 - i + i = RC 6 - i         (4)

1 < i < 6

Based on the formula 4 and formula 1, 2, we can deduce the following formula.

Rp = LC    E (RC 6-i, K 6_J e E (RC 6-, K 6-,J = LC6-,

LP i = RC ₆, e E ( LC 6 - i ,K 6 -J e E ( LC 6 - i ,K 6 - i J = RC ,  (5)

1 < i < 6

As can be seen from formula 5, RP i = LC 6- i , LP i = RC 6- i . The ciphertext is restored to the plaintext after six rounds iterative computation. The follow figure demonstrates the decryption procedure of the LWSEA algorithm, which is similar to the encryption process. However, the using sequence of the child-key K i (1≤ i ≤6) is in the opposite.

Cihpertext Input (48bit)

Left data                                       Right data

LC 0 (24bit)                   RC 0 (24bit)

K 6

E

LC 1 =RC 0     K₅ RC 1 =LC 0 ⊕ E(RC 0 , K 6 )

+ E

..

.. ..

LC 5 =RC 4     K 1   RC 5 =LC 4 ⊕ E(RC 4 , K 2 )

+ E

RC 6 =LC 5 ⊕ E(RC 5 , K 1 )       ^LC6^=RC5

Plaintext =LC 6 RC 6

Fig. 3: Decryption procedure of LWSEA algorithm

• C.    The design of nonlinear scrambling function

If we only adopt round-function E and the key K to do several rounds of iterative calculation in the LWSEA algorithm, the output ciphertext have not the distinct “avalanche effect”, namely the tiny changes in plaintext will not bring about great changes in ciphertext, which maybe result in LWSEA can’t resist the attack of the characteristics analysis. The famous DES algorithm, which is based on the same Feistel Cryptosystem Structure, adopts scrambling functions to improve the “avalanche effect” of ciphertext. But the design details of the functions haven’t been released, which bring in potential security hazard. We put forward new scrambling functions according to data scrambling idea, named S -box. In the LWSEA algorithm, we use three different S -box functions to finish the data-scrambling work and improve the ciphertext’s randomness. The method is: After every round encryption is ended, the length of RC i-1 is expanded to 36bit based on table F , and then K i redo encryption calculation with expanded RC i-1 . The result is average divided into three pieces B 1 , B 2 , B 3 whose length are all 12 bits, and then using three different S functions to do nonlinear scrambling to them respectively, viz. S i ( B i ), 1≤ i ≤3. After disposal of S functions, the length of B _i decrease to 8bit. The three new B _i are connected as a new input data for next round encryption calculation.

The function of S is to do nonlinear scrambling for data, which can prevent attacker to crack the ciphertext by differential analysis. So the S has vital purpose which is the security base of LWSEA algorithm. LWSEA only adopts three different S functions, which is less than DES that adopts eight S functions. The content of S in LWSEA is consisted of a 256×16 matrix, but content of S in DES is consisted of a 16×4 matrix. The biggish matrix will make S function possess better “avalanche effect” and security level, furthermore, the fewer quantity of S will decrease the cost of encryption algorithm. These special characters make LWSEA is more suited for the security requirements of resource-restrained WSNs node. The content of S function is the main weapon to cope with differential analysis attack. So we refer the ideal of nonlinear infinite diffusion in Rijndael algorithm to design three different S functions. But the matrix in those S functions is huge, the paper don’t list their content.

The length of input data to S functions is 12 bits. Its front 4 bit denotes the row number in matrix, and its back 8 bit denotes column number in matrix. Based on row and column number, we can find the position of the displacement data. For example, if the input data to S ₁ function is 111011010101, and then its front 4 bit is (1110) 2 =(14) 10 , viz. 14^th row, as well as its back 8 bit is (11010101) 2 =(213) 10 , viz. 213^th column. The data with the position of 14^th row and 213^th column in S 1 matrix is 178, viz. (178) 10 =(10110010) 2 , and then LWSEA use 10110010 to displace the 111011010101, thus the original data with 12 bits length decrease to a new data with 8 bits length.

After introducing scrambling functions S into LWSEA, the chaos and disorder degree of ciphertext have great improvement. The “avalanche effect” of encryption becomes obvious, which is proved in the subsequent experiments. The operation process of S function is shown in follow figure.

Expanding displacement

RP i-1 (24 bit )—J EX Table1—► RP i-1 (36 bit )

K i (36 bit )--------► ⊕

B 2 (12 bit )       B 3 (12 bit )

B 1 (12 bit )

B ^' (8 bit )           B ^' (8 bit )          B ^' (8 bit )

Packet Aggregation

B ^''(24 bit )

Fig. 4: Scrambling procedure of S function

• VII.    Experiment and data analysis

To test the performance of the LWSEA algorithm, we have done many experiments in a variety of ways, and adopt famous symmetry encryption algorithm DES as its reference. In experiment procedure, we obtain many valid data that help to improve the design of LWSEA. The below content list several representative experiments to demonstrate its eximious characters.

• A.    Comparison of avalanche effect

We achieve the LWSEA algorithm with VC++7.0, and then download the standard DES program from the Internet as a contrastive reference. We use two simple plaintexts of 64 bits: “aaaaaaaa” and “zzzzzzzz” as the testing data, and then encrypt them with LWSEA and DES respectively. After the above process is completed, we continue to do a letter changes in these plaintexts, viz. “aaaaaaaz” and “zzzzzzza”, and respectively encrypt them with LWSEA and DES again. Encryption results are shown in following table.

Table 4: Encryption results of two algorithms

Encryption Algorithm	Encryption Key	Plaintext (letter)	Ciphertext (Hexadecimal number)
LWSEA	QWERTY UIOPASD FG	aaaaaaaa	9570DA3BDB46533C
		aaaaaaaz	B67CD6B21468F89P
		zzzzzzzz	K51AABE563406EE6
		zzzzzzza	E5842B6A642EDE52
DES	QWERTY UI	aaaaaaaa	75E2732D941BC7C0
		aaaaaaaz	496347279A1548DE
		zzzzzzzz	89DE09BED9CB7066
		zzzzzzza	A13272856CED7D8F

From table IV, we can find that the plaintext has big difference from the ciphertext produced by LWSEA algorithm. There is a letter change in plaintext; the changed content in the ciphertext respectively achieve 57 bit and 58 bit. In DES algorithm, the changed content in the ciphertext respectively achieve 61 bit and 62 bit. It is proved that the LWSEA algorithm has a very good “avalanche effect”, and its encrypting intensity is close to DES algorithm. While LWSEA algorithm has much less encryption rounds than DES, and the scrambling function S is also simple than that of DES. So the cost of the former will be smaller than the latter, but the former get the similar security level with the latter.

• B.    The comparison of encryption speed

  In the subsequent experiment, we use the type of TS1 Wireless sensor produced by ISI Company to test the encryption time and resource cost of these two kinds of algorithms. TS1 Wireless sensor is powered by two 5# dry batteries, and its CPU is the EM78820 microprocessor which is 32-bit field length and run at 6MHZ. Its RAM is 512KB and working frequency is 2.4 GHz. Network protocol is IEEE 802.15.4, and data transfer rate is high up to 320Kbps. Data receiver uses the type of BS1 wireless receiver produced by ISI Company. Through set appropriate commands to BS1, we can analysis out the encryption cost of two algorithms in the TS1 Wireless sensor by the received data in BS1.

We have designed 2100 group data each contain 48 bit, and make the TS1 wireless sensor encrypt them by using LWSEA algorithm and DES algorithm separately, and then return the encryption results to the data receiver BS1. We have analyzed those results and get a conclusion as is shown in following figure.

of DES of DES of LWSEA of LWSEA

Time

Time

Time

Time

—♦—Encryption

—■— Decryption

—▲—Encryption

Decryption

Number of Packets

Fig. 5: Encryption/Decryption time of two algorithms

The figure 5 has shown average encryption time of LWESEA algorithm and DES algorithm. Judging by the figure 4, we can find that the encryption speed of LWESA algorithm is much faster than that of DES algorithm, which is caused by less encryption rounds and simple scrambling function of LWESEA algorithm. LWESEA algorithm is more suitable for structuring large scale WSNs and the occasions whose real time requirement is high.

• C.    The comparison of CPU and RAM occupation

In the TS1 wireless sensor, we use LWSEA algorithm and DES algorithm to encrypt identical data separately, and then make use of the internal watching system of TS1 to observe the occupation rate of CPU and RAM. The comparison result is shown as follow figure.

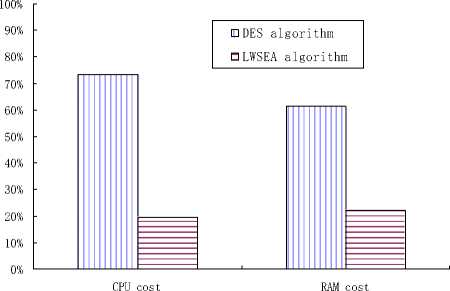
Fig. 6: CPU and RAM cost of two algorithms

From the figure 6 we can find that the average RAMoccupancy rate of LESEA algorithm is only 38 percent of the DES algorithm, while the average CPU-occupancy rate is only 31 percent of the DES algorithm, so the LWSEA algorithm cost is much lower than DES algorithm.

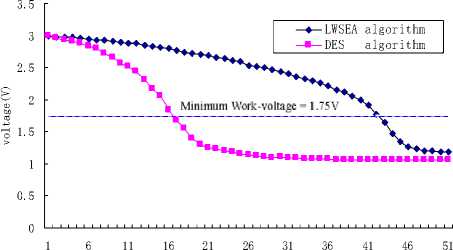
• D.    The comparison of battery cost

The experiment used two same TS1 wireless sensors and two pairs new 5# batteries produced in same batch. We respectively used LWSEA algorithm and DES algorithm to repeatedly encrypt same a group data in the two sensors. When all the electronic power has been exhausted, the experiment is ended, and then we get follow data in figure 7.

Running time(hour)

Fig. 7: Battery cost of two algorithms

From figure 6 we can find that the sensor which is running the DES algorithm will exhaust its electronic power after 16 hours, while the sensor which is running the LWSEA exhaust its power after 43 hours. So the experiment indicates that LWSEA algorithm can effectively save battery power and raise the surviving time of sensor.

• VIII.    Conclusion

WSNs sensor is deployed in the opening wireless environment, so its signal can be intercepted easily. Secure transmission of data has been the prominent problem for WSNs. The usual method is to adopt encryption technique. But WSNs sensor mostly uses battery to provide power, and the ability of CPU calculating and the RAM capacity are all extremely limited as its power resource. So it isn’t suited for WSNs sensor to use complicated encryption algorithm.

The paper proposed a new symmetric encryption algorithm on the basis of Feistel Cryptosystem Structure: LWSEA. Comparing to the standard DES algorithm, LWSEA uses less encryption rounds and shorter data packet, and the simplified Scrambling function. But it adopts longer-bit Key and circular interpolation method to produce child-key. Through those improvement measurements, the working cost of LWSEA reduce too much while its security degree only decrease little.

Firstly, we test the “avalanche effect” of LWSEA algorithm, and find that the data chaos degree of ciphertext is high and close to DES algorithm. Secondly, we run LWSEA algorithm and DES algorithm separately on TS1 wireless sensor, and test the encryption speed, encryption cost and battery consumption during two different algorithms. The result shows that LWSEA algorithm has prodigious advantage in all aspects. These all indicate that LWSEA algorithm is very suited for resource-restrained WSNs sensor.

In the following work we will study the features of manifold usual WSNs sensor, and analyze their commonness and special requirements, and do further improvements for LWSEA algorithm make which adapt to the need of security and cost of most WSNs sensors.

Acknowledgment

This work was supported by Intergovernmental Scientific and Technological Cooperation Project (Ukraine-China, No. CU01-11), and Outstanding Youth Science and Technology Innovation Team Project of Hubei Polytechnic University (13xtz10).