A low-complexity algorithm for contrast enhancement of digital images

Published Online February 2018 in MECS

Over the last decades, substantial progress has been made in the fields of digital image processing and computer vision by both professionals and researchers [23]. Contrast enhancement is an important image processing field that plays an essential role in improving the visible quality for a variety of image-related applications [4]. Moreover, it is considered an important processing step in different scientific applications [7]. The insufficient contrast in digital images can occur due to many reasons, including the deficient expertise of the operator and the use of an inefficient device for image acquisition [1]. Commonly, the contrast is generated due to variance in luminance between two adjacent surfaces. Accordingly, the contrast of a given image can be determined via the intensity difference of an object with other objects. Thus, if the image intensities have a restricted distribution within a limited range, the contrast of the observed image would become low and its details would be obscured.

The low-contrast effect reduces the visual quality of an image and thus, it should be handled properly to provide acceptable quality for digital images [9]. Hence, it is desired to redistribute the intensities of a given image to the entire dynamic range in order to improve its contrast and provide an adequate representation for its information [10]. Generally, the methods for contrast enhancement of can be categorized into direct [2, 3] and indirect [5, 6] methods. In the direct methods, a certain contrast term is used to define the image contrast. Since a digital image contains simple and complex patterns, using such contrast terms may fail to measure the contrast in a variety of images [31]. On the contrary, indirect methods try to improve the image contrast by redistributing the probability density. This means that the intensities of a given image can be reallocated within the natural range without using a certain contrast term [1].

Most of these methods are implemented either in the spatial domain or the frequency domain. Accordingly, the image is processed as it is in the spatial domain, whereas in the frequency domain, the image is first transformed to its frequency version, then the processing occurs; after that, an inverse transformation is applied to view the image in the spatial domain [20]. Histogram-based methods for contrast enhancement are the most famous indirect methods due to straightforward implementation [8]. Despite the major advantages of these indirect methods, many of such tend to produce undesirable degradations (e.g. under-saturation, over-saturation) to the processed images [21]. Hence, a low-complexity algorithm is introduced in this article to process low-contrast images rapidly and efficiently without introducing any undesirable degradations. The proposed algorithm is developed experimentally and consists of 4 distinct steps, for which each step provides a positive contribution to the enhancement process. In addition, the enhancement ability of the proposed algorithm is controlled using a single parameter. The developed algorithm is evaluated by a dataset of synthetic and real degraded low-contrast images collected from various internet websites. The synthetic degraded images are used for comparison purposes, while the real degraded images are used for experimental purposes [32]. Moreover, the quality of the obtained results is measured using two reliable image quality assessment (IQA) metrics. Likewise, the proposed algorithm is compared with three well-known contrast enhancement methods. To end with, most of the available contrast enhancement methods employ the concept of histogram equalization. In addition, most of the available contrast enhancement methods that provide acceptable results have a complex structure with a high number of calculations. However, the proposed algorithm has a simple structure and does not utilize the concept of histogram equalization. To test the processing ability of the proposed algorithm, various computer experiments on different low-contrast images are performed. The rest of the article is ordered as follows: in Section II, an abridged review of literature is delivered. In Section III, the proposed algorithm is explained in detail. In Section IV, the results and their related discussions are provided. Finally, a concise conclusion is given in Section V.

the input image and its low-pass counterpart to the input image itself. Furthermore, the Gaussian mixture modeling based algorithm [28] processes an image by modeling its gray-level distribution to generate gray-level intervals. The resulting image is created by changing the gray-level of pixels in each determined interval to the suitable output gray-level interval in relation to the cumulative distribution function and the dominant Gaussian element of the input interval.

Another interesting method is the spatial entropy-based enhancement [29], as it distributes the spatial positions of gray-levels of an image rather than gray-level distribution. The spatial distribution is calculated for each gray-level by a histogram of spatial positions for all pixels with the same gray-level. From the spatial distributions of image gray-levels, the entropy measures are computed to generate a distribution function, which is also mapped to another distribution function to attain the final enhancement. To end with, the method introduced in [30] works by iteratively solving a nonlinear diffusion equation. Through the process of diffusion, surround suppression is included in the conductance function to improve the diffusive strength in certain areas of the image. As seen from the above-reviewed methods, various low and high intricacy concepts have been utilized for the purpose of contrast enhancement. Thus, developing a new algorithm that utilizes a simple concept and achieves acceptable enhancement is desirable in many computer vision and image processing applications.

• III.    Proposed Algorithm

• II.    Related Works

In this section, various contrast enhancement methods are addressed to highlight some of the important concepts that have been utilized previously. In view of that, the dynamic histogram equalization [24] is an enhancement technique that works by partitioning the histogram of the input image depending on local minima and allocates certain gray-level ranges for every partition before processing them independently. The aforementioned partitions undergo further tests to avoid having dominating partitions. Another method of interest is fused logarithmic transform [25], as its enhancement is achieved by fusing the degraded image and its logarithmic counterparts.

In addition, the intensity surface stretching technique [26] processes an image by stretching its intensity surface to the maximum range with consideration to the distances between the pristine intensity surface as well as the upper and lower intensity surfaces, which are created automatically from the pristine intensity surface by calculating the gamma transform and Gaussian smoothing. Moreover, the algorithm proposed in [27] processes an image using the theory of partitioned iterated function system (PIFS). The PIFS is utilized to generate a low-pass counterpart of the input image. The enhanced image is generated by adding the difference of

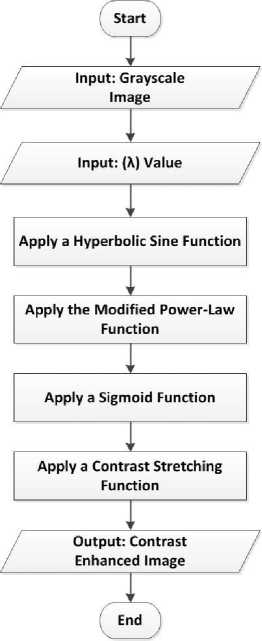
Fig.1. The framework of the proposed algorithm.

The proposed algorithm is developed experimentally with intention of providing an adequate enhancement for images with poor contrast. The framework of the proposed algorithm is illustrated as in Fig. 1.

The proposed algorithm starts by applying the hyperbolic sine function as an initial processing stage to provide a simple contrast modification. This function can be described as follows [11]:

e - e s =-----

where, ( x ) is the input low-contrast image, ( s ) is the resulting image from the hyperbolic sine function. Then, the result of the previous stage is processed by a modified version of the famous power-law function. The standard power-law function can be written as follows [12]:

p = c * s ^x

where, ( c ) is a scalar that controls the brightness of the power-law function, ( λ ) is a scalar that controls the enhancement of contrast. The values of these scalars must fulfill ( c , λ > 0), where a higher ( c ) value leads to a brighter result and a higher ( λ ) value leads to a less bright and contrast improved result. Thus, the above standard function is modified by removing the scalar ( c ) because it can lead to an undesirable increase in the brightness of the processed image. Hence, the modified power-law function is written as follows:

y = s

Л

where, ( y ) is the resulting image from the modified power-law function. Afterwards, the standard sigmoid function is utilized to remap the image pixels in an “S” shape, which can provide further contrast enhancement. The used sigmoid function can be written as follows [13]:

w =

1 + e " y

where, ( w ) is the resulting image from the standard sigmoid function. As a final stage, a contrast stretching function is applied to remap the image pixels into their natural dynamic range [22]. The used stretching function can be described as follows [14]:

f =

w - min ( w ) max ( w ) - min ( w )

where, min and max are the minimum and maximum pixel values, respectively. ( f ) is the final result of the proposed algorithm. Finally, the benefits of this algorithm are fast processing speed, low computation cost, and artifact-free images with acceptable quality results.

• IV.    Results and Discussion

In this section, the essential computer experiments and their related discussions are provided to validate the processing ability of the proposed algorithm. To perform proper experiments, real-degraded images were used for experimental purposes, and synthetic-degraded images were used for comparison purposes. The dataset of this study was collected from different imaging databases across the internet. Regarding the comparable methods, several contemporary and reliable methods were chosen, in which the proposed algorithm was compared with three of such methods namely, successive mean quantization transform (SMQT) [15], gradient distribution specification (GDS) [16], and exposure based sub image histogram equalization (ESIHE) [17].

Regarding the used IQA metrics, two well-known fullreference IQA metrics of universal image quality index (UIQI) [18] and structural similarity index (SSIM) [19] were used to measure the quality of the results of comparisons. The results of these metrics are constant numbers, in which values near 1 indicate high-quality results and values near 0 indicate low-quality results. The experimental results obtained from processing various real-degraded grayscale images are shown in Fig. 2 – Fig. 4. The results of the performed comparisons can be seen in Fig. 5 and Fig. 6. The recorded accuracy by the UIQI and SSIM metrics are provided in Table 1, Fig. 7 and Fig. 8. From the obtained experimental results in Fig. 2 – Fig. 4, it can be seen that the proposed algorithm provided visually pleasing results. Moreover, the recovered images show natural brightness, acceptable contrast with no visible flaws. However, the value of λ differs from one image to another due to the noticeable differences in the nature of the used images and the variance in contrast levels for each processed image.

From the obtain comparison results in Fig. 5 – Fig. 8 and Table 1, it is evident that the proposed algorithm performed the best in terms of recorded accuracy and perceived quality, as it recorded the best UIQI and SSIM scores, as well as, it provided clear and unblemished results. This is significant because the proposed algorithm has a simple structure with a non-iterative nature and utilizes few calculations to achieve its task. Regarding the SMQT method, it provided very good performances especially when the contrast of the processed image was severely reduced. However, its high computation and iterative natures made it slow in producing the desired results. Moreover, this method tends to increase the darkness of dim areas in the processed images. Such limitations can lead to unclear results, especially for images with many dim areas.

Regarding the GDS method, it provided moderate contrast enhancement, yet the low-contrast effect is still visible in the processed images. In addition, this method is somewhat slow due to its high computations utilization. Regarding the ESIHE method, it provided good performance when the processed image had minor contrast reduction. However, it provided poor performance when the processed image had major contrast reduction. Accordingly, the output of this method has low brightness and poor contrast. Such artifacts can limit the use of this method in certain image processing applications. Finally, developing an efficient, yet uncomplicated algorithm for contrast enhancement is a challenging and significant task. However, this task is clearly achieved successfully, as the proposed algorithm provided visually pleasing results with no visible artifacts and outperformed the comparable algorithms in terms of visual quality and scored accuracy.

Fig.2. The obtained results of the proposed algorithm. (a1 – c1): real-degraded images; (a2 – c2) from left to right: images recovered by the proposed algorithm with λ=1.1, λ=1.6, and λ=0.9, respectively.

Fig.3. The obtained results of the proposed algorithm. (a1 – c1): real-degraded images; (a2 – c2) from left to right: images recovered by the proposed algorithm with λ=0.5, λ=0.4, and λ=0.25, respectively.

Fig.4. The obtained results of the proposed algorithm. (a1 – c1): real-degraded images; (a2 – c2) from left to right: images recovered by the proposed algorithm with λ=4, λ=1.1, and λ=1.5, respectively.

Fig.5. The results of the achieved comparison. (a) True image; (b) Contrast reduced image by 40%; images from (c – f) are recovered by: (c) SMQT; (d) GDS; (e) ESIHE; (f) proposed algorithm with λ=1.1;

Fig.6. The results of the achieved comparison. (a) True image; (b) Contrast reduced image by 80%; images from (c – f) are recovered by: (c) SMQT; (d) GDS; (e) ESIHE; (f) proposed algorithm with λ=1.5;

Table 1. The recorded accuracy of the used IQA metrics for the comparable methods.

#	Comparatives	Fig. 5 (UIQI)	Fig. 5 (SSIM)	Fig. 6 (UIQI)	Fig. 6 (SSIM)
1	Degraded Image	0.9049	0.8791	0.8428	0.5447
2	SMQT	0.9928	0.9155	0.9860	0.8600
3	GDS	0.9482	0.8792	0.9155	0.7690
4	ESIHE	0.9956	0.9223	0.7463	0.7289
5	Proposed Algorithm	0.9968	0.9237	0.9917	0.9112

Note: the bold values indicate the best-achieved results.

Accuracy Chart (UIQI)

■ Fig. 6 (UIQI) ■ Fig. 5 (UIQI)

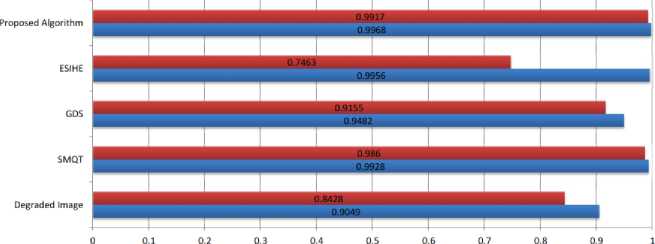
Fig.7. The graphical chart for the obtained accuracy results by the UIQI metric.

Accuracy Chart (SSIM)

■ Fig. 6 (SSIM) ■ Fig. 5 (SSIM)

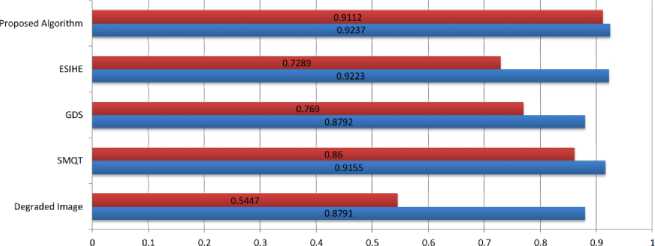
Fig.8. The graphical chart for the obtained accuracy results by the SSIM metric.

• V.    Conclusion

In this article, an innovative algorithm for contrast enhancement of digital images is introduced. The proposed algorithm utilizes four distinct functions of hyperbolic sine, modified power-law, sigmoid and contrast stretching to achieve the desired enhancement. The obtained results were benchmarked with synthetic and real degraded images and compared with the three well-known contrast enhancement methods of SMQT, GDS, and ESIHE. Furthermore, the accuracy of the obtained results was measured using two well-known metrics of UIQI and SSIM. From the obtained results, it can be seen the proposed algorithm provided satisfying results and outperformed the comparable methods since it scored the best in terms of visual quality and IQA metrics. Accordingly, the proposed algorithm provided a natural appearance with no visible errors to the processed images, wherein such acceptable results can highly support the validity of the proposed algorithm. Finally, the use of simple methods for contrast enhancement is desirable in many image-related applications.

Acknowledgment

The authors wish to thank the respectable reviewers and editors for their helpful comments.