A Metaheuristic Algorithm for Job Scheduling in Grid Computing

Published Online May 2014 in MECS

The popularity of the internet and the availability of broadband networks need to use of distributed and multiuser computers are provided. Recent researches in the computing science introduced a new issue called "Grid Computing" [1].

Grid computing is an approach to solving large-scale problems in science, engineering, and business [2]. Grid computing involves resource sharing, resource management, information management, job scheduling, and so on. The aim of grid computing is to use the computing resources available for complex computing by sites, which were distributed geographically. The main idea of grid computing is that sharing resources between layers of software can be used for transparency and security. This layer of software is responsible for virtualization resources, search resources and manage running applications.

Computational grids, in the simplest sense are distributed computations. The purpose is thought a simple virtual computer while large and powerful that has the ability to manage a wide collection of computers be created. This collection of a group of heterogeneous systems connected together with various combinations of shared resources.

Scheduling is one of the most important problems in computational systems like grid. To increase the efficiency of the grid, a scheduler is required to work properly and efficiently. Unfortunately, the dynamic nature of the grid and various demands of users have caused the complexity of grid scheduling. The dynamic nature of the grid means that the performance of grid resources is always changing.

Heuristic scheduling algorithms are often used in heterogeneous computing environments [3, 4, 5]. In dynamic grid environments, the execution time and workload cannot be determined in advance. Therefore, grid scheduling needs predictive models.

In this paper, CUckoo-Genetic Algorithm (CUGA) is presented as a metaheuristic algorithm to solve job scheduling problem in grid environment. CUGA is inspired by cuckoo search optimization and genetic algorithm. It has the capability of global searching, and it has fewer algorithm parameters than genetic algorithm. Through a serial of simulated experiments, our results illustrate that CUGA algorithm is effective for job scheduling in computational grids. In addition, CUGA could avoid trapping in a local minimum effectively.

The paper is organized as follows. Related works are reviewed in Section 2. In Section 3, job scheduling in grid computing is described. In Section 4, we will have a brief overview of cuckoo optimization algorithm. Genetic algorithm will be discussed in Section 5. In Section 6, CUGA algorithm will be introduced. Job scheduling using CUGA will be discussed in Section 7. Experimental results are explained in Section 8 and conclusion is presented in Section 6.

• II.    Related works

Many studies have been done in the area of job scheduling in computational grids. Intelligent optimization methods can be applied to resolve such complex problems [6]. On the other hands, metaheuristic algorithms are widely used to solve a variety of NP-hard problems.

Aggarwal [7] proposed a scheduler based on GA for grid environment. In this research, a Directed Acyclic Graph (DAG) represented for each job takes into account arbitrary precedence constraints and arbitrary processing time. The results show that the scheduler reduces makespan and idle time of the available computing resources.

Zhang represented a heuristic approach in [8] based on PSO algorithm to solving job scheduling problem in grid environment. His experiments show that PSO algorithm is able to do a better scheduling compared to GA.

Wang proposed Genetic-Simulated Annealing (GSA) algorithm in [9], which combines GA with Simulated Annealing algorithm (SA) for grid job scheduling.

Mathiyalagan and Suriya in [10] used Ant Colony Optimization (ACO) for scheduling in grid environment. In this research, ant colony begins with no solution. Each ant makes own solution with decisions by limitations and heuristics. The ants are allowed to share information about good solutions; it is necessary to update the pheromone sequence.

Umale in [11] used ACO hybrid with Genetic Algorithm in Grid environment that provides a two-level decision called TLDA. At first initial schedule is created using ACO, then they used GA to modify the scheduler. TLDA algorithm reduces the execution time of applications. This algorithm is dynamically changed during the execution of works and resources to take into consideration. TLDA has better performance in comparison with ACO and GA.

Pooranian in [12] proposed a new hybrid-scheduling algorithm that combines GA and the Gravitational Emulation Local Search (GELS) algorithm denotes GGA. The noteworthy feature of GGA scheduler is that it decreases runtime and the number of submitted tasks whose deadlines are missed. A comparison of the performance of the proposed joint optimal scheduler to similar methods shows that it produces more optimal computation time.

• III.    Job scheduling in grid computing

Scheduling is the process of allocating a finite set of jobs to resources [13]. In other words, scheduling is the process of allocating jobs in an effective and organized combination to achieve goals. These jobs usually require the use of resources that this resource in terms of numbers and in terms of access time is limited [14]. However, jobs may be needed to run at a specific time and in a specific order. The aim of scheduling is to find an optimal resource and allocate a job to the resource. In this process, a scheduler should overcome heterogeneous resources and maximize overall system performance. The concept of scheduling is shown in Fig 1. As you can see in the figure, several jobs may be assigned to a resource.

In this case, a set of n jobs and m machines are shown. Each job i is composed of n i operations, which we show O_i1,O_i2,O_i3,^,O_ini . The goal is to find a scheduling that will have the least possible time to complete all the jobs.

Fig. 1. Job scheduling in grid computing

Cases, which are considered by grid scheduler, include:

• •    Efficiency of CPU : CPU keeps busy as much as possible.

• •   Throughput: Number of jobs completed in each

unit of time.

• •    Return time: The running time of a particular process.

• •   Response time: The time between the first

request and receiving a response

Grid scheduling process can be considered in three steps:

• 1.    Detect and separate resources

• 2.    Select and schedule resources based on specified goals

• 3.    Assign jobs to resources

The emphasis of scheduling algorithms is on the second step.

• IV.    Cuckoo optimization algorithm

  Cuckoo Optimization Algorithm is one of the evolutionary techniques, which was introduced in 2009 by Yang and Deb [15]. This algorithm is inspired by the lifestyle of a bird called Cuckoo. This lifestyle is one of the rarest brood parasites in nature. This bird did not make nest for itself and it used the nests of other birds for laying eggs. The ability to create eggs like the bird host is reinforced in cuckoo bird. If the bird's host discovers eggs that are not theirs, it throws away or leaves the nest, and it makes a nest in other places. Cuckoo eggs are the bigger size of the host bird until cuckoo brood would hatch soon. When the host bird's eggs are thrown out of the nest or demand food so much to other broods, die of hungry. When the cuckoo brood grows and becomes a mature bird, they continue the mother's life instinctively.

In order to solve an optimization problem, it is necessary that the values of parameters' problem be formed as an array. In GA and PSO terminologies, this array is called “Chromosome” and “Particle Position”. However, in COA it is called “habitat” [16]. To start optimization with COA algorithm, a candidate habitat matrix is generated. Then some randomly produced number of eggs is supposed for each of these initial cuckoo habitats. In nature, each cuckoo lays between 5 to 20 eggs. These values are used as the upper and lower bounds of eggs assigned to each cuckoo at different iterations. Other habit of real cuckoos is that laying eggs within a maximum distance from their habitat. This maximum area will be called “Egg Laying Radius (ELR)”. Each cuckoo has an ELR, which is appropriate with TE, the total number of eggs, NE, number of current cuckoo’s eggs, and variable limits of varhi and varlow. Accordingly, ELR is defined as (1):

ELR= ос X — X (var^, — var;_01v) (1)

where α is an integer supposed to handle the maximum value of ELR .

When young cuckoos grow and become mature, they live in their own area and make society for some time. But when the season for egg laying approaches, they move to new habitats with the most similar host eggs and with more food for new young birds. After that cuckoo groups are formed in different areas, the society with the highest fitness value is selected as the goal point and other cuckoos move to that point.

At what time mature cuckoos live in that environment identifying which cuckoos belong to which groups is difficult. Now for those groups of cuckoo that are identified efficiency value is calculated. The maximum amount of efficiency is determined by the goal group and consequently that group’s best habitat is the new destination habitat to move cuckoos.

While moving toward a goal point, the cuckoos do not fly all the way to the destination habitat. They only fly a part of the way and have a deviation. Fig. 2 shows pseudo-code of COA.

• 1.    Initialize cuckoo habitats with random points.

• 2.    Define ELR for each cuckoo.

• 3.    Let cuckoo lay eggs inside their corresponding ELR.

• 4.    Kill those eggs that are identified by host birds.

• 5.    Eggs hatch and chicks grow.

• 6.    Evaluate the habitat of each newly grown cuckoo.

• 7.    Limit cuckoos’ maximum number in environment and kill those that live in worst habitats.

• 8.    Cuckoos find best group and select goal habitat.

• 9.    Let new cuckoo population move toward goal habitat.

• 10.    If stop condition is satisfied end , if not go to 2.

Fig. 2. Pseudo-code of Cuckoo Optimization Algorithm

• V. Genetic algorithm

  Genetic algorithm was first introduced in 1970 by John Holland [17]. In general, genetic algorithm is comprised of the following components:

Chromosome : In genetic algorithms, each chromosome represents a point in the search space, and a possible solution to a considerable problem. Their chromosomes (solutions) are composed of a number of genes (variables). To represent chromosomes, it is usually used binary encoding (bit strings).

Population : A population is a set of chromosomes. By the influence of genetic operators on the population, the new population will be formed with the same number of chromosomes.

Fitness function : In order to solve each problem by using of genetic algorithms, a fitness function must be invented for that issue. For each chromosome, this function returns a negative number that indicates competence or ability of the individual chromosomes.

In genetic algorithms, genetically operators are used during the reproductive stage. The impact of these operators on a population produced the next generation. Selection, crossover, and mutation have the most commonly used operators in Genetic algorithms.

Selection operator: By means of this operator, a number of chromosomes are selected for reproduction. Elegant chromosomes are more likely to be selected for reproduction.

Crossover operator: During the crossover, random parts of chromosomes are exchanged with each other. The children contain combination of qualities that their parents have. Good qualities of parents are gathered to produce new children.

Mutation operator: After the crossover on chromosomes, mutation operator is granted. The function selects a gene in a chromosome randomly and then alters gene content.

• VI.    CUGA: The proposed algorithm

In this section, a new optimization algorithm, CUGA, is introduced which involves concepts of cuckoo optimization algorithm and genetic algorithm. The disadvantage of GA requires fairly long processing time to calculate, and it needs to develop a test to define the optimal parameters. PSO algorithm has been compared with genetic algorithm and it has been shown the PSO results shorter time to complete jobs. However, its disadvantage is that it often can not reach the quality of solutions to be compensated by increasing repetitions. One of the reasons is that in PSO algorithm particles converge to a value among a certain point in general and personal positions. Another disadvantage is the rapid rate of transfer data between particles that increases the probability of being in a local optimal.

The advantages of cuckoo optimization algorithm compared with other optimization methods are:

• 1.    Faster convergence.

• 2.    Higher accuracy.

• 3.    Search with variable population (because of the destruction population in unsuitable regions).

• 4.    Move total population toward better solutions with destroyed unsuitable solutions.

• 5.    The ability optimization of problems with highdimensional.

• 6.    Having the ability to avoid becoming trapped in a local minimum.

The efficiency of genetic algorithms is highly dependent on how the chromosomes are represented, so finding a optimal sequence of chromosomes is a hard problem. Our proposed algorithm is combine cuckoo search algorithm with GA to address this weakness. A combination of a GA and COA is used because COA searches the problem space well and finds better solutions compared to other local search algorithms such as PSO and GA. GA searches inherently parallel and it can search several aspects of a problem space simultaneously. Furthermore, the convergence of GA is slow for global optimization and has been proven unstable in different implementations. The efficiency of GA can be improved by benefiting from algorithms such as COA.

CUGA is composed of two stages: the first stage complies with cuckoo optimization algorithm and the second stage pursues genetic algorithm. In CUGA algorithm at the end of the first stage, a population of cuckoo eggs in an area that has the greatest chance for growth is feed to the second stage as the initial population.

In second stage of CUGA, single point crossover is utilized. Afterward, mutation operator will affect the new population. Using this operator, a cuckoo is selected randomly from the population and it is replaced by another one from the population. After the mutation operation, the cuckoo population produced is known as the new generation in which the optimal solution is stored and then the steps have been repeated again. Fig. 3 shows the pseudo-code of CUGA algorithm.

Begin

Generate initialize cuckoo habitats.

Dedicate some eggs to each cuckoo.

Define ELR for each cuckoo.

While (iteration < maxIter) and not (stop Criterion) Initialize number of eggs for each cuckoo.

Kill those eggs that are recognized by host birds.

Keep the best solutions (or nests with quality solutions).

Using best cuckoo on last Crossover Rate% of cuckoo population.

Mutation of all population.

End While

Postprocess the results and visualization.

end

• Fig. 3. Pseudo-code of CUGA algorithm

• VII.    Job scheduling in grid computing using CUGA

We used CUGA for job scheduling in grid computing. The aim of CUGA for scheduling is present at optimal method to allocate jobs to machines to decrease completion time, resource efficiency, and increasing speed of convergence. CUGA is utilized in problems with complex assumption.

In this paper, each job is composed of n operations, which will run on m machine. When a job log in may or may not need all machines or a special machine is needed more than once, the scheduler is faced with many problems so for this issue, assumptions, and rules are considered:

• 1.    There is no constraint on processing time of each job on machine.

• 2.    There is no run out time. Each job should be processed to its finishing point [18].

• 3.    All jobs enter the system at zero time and can start execution immediately. It means that there is no constraint on assignment time.

• 4.    All jobs that entered the system must use all of the machines. In other words, if there are n jobs and m machines, each job must consist of m operations that each of them will be executed exactly on one of machines.

• 5.    The order of operations of each job on machines can be changed from one job to others. For example, in the environment with 3 machines job i may be processed on machine 1, 3, 2 and job j may be processed on machine 2, 1, 3

• 6.    Main objective is to minimize the make span. Explicitly, jobs must be organized on machines in order to minimize the overall execution time of jobs.

• 7.    One machine can process at most one operation at a time.

• 8.    Every job can be performed just on one machine at a time [18].

• 9.    Operations can not be interrupted, which means operation execution is atomic.

• 10.    There is not any crashed machine, which means all the machines are always available.

• 11.    Machines may be idle during overall execution process.

• 12.    The only limitation in this problem is that of the priority order of the operations of each job. A job has to follow the order of operations assigned to it and can not contravene even one constraint [19].

respectively.

Fig. 4 shows the diagram of using CUGA algorithm to solve job-scheduling problem. The cuckoo’s egg corresponds to a solution of the problem. The implementation steps are described in the following.

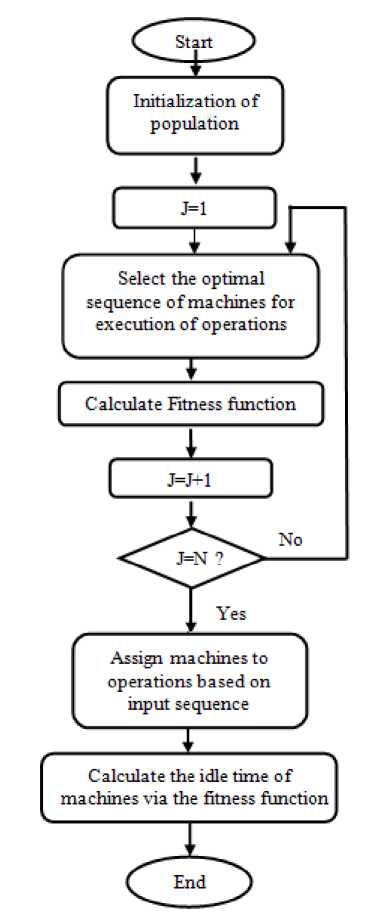
Fig. 4. Outlines of using CUGA, the proposed algorithm, for solving job scheduling

Generate the initial population: Generating initial population is base of beginning algorithm. Population of cuckoos mapped into a set of jobs. Each cell of habitat has mapped to resources that are located in operation of each job. The items received at this stage, including n is the number of jobs, o the number of operations (because each job consist of several operations), m is number of machines, V_n*m is the order of operations for each job and also the time required for each operation, the algorithm tries to find the optimal solution. We assume that the number of machines with the number of operations is equal: m=o .

Select an optimal order of machines: The order of run-time operations on each machine is different. For example, in an environment with four jobs and three machines one job may employ machines 1, 3, 2 and the other one used machines 1, 2, 3 to be finished. In this step we are looking for an optimal sequence of machines. So for each job a[i]m*m (m is the number of machines and the number of operations) minimum run time should be resulted. However, the performance of a machine to do a job alone is not determinative, but all machines have less time to perform a job with the assumption that a machine should not be used more than once.

Fitness function calculation: To ensure this assumption that each operation at any time can only run on a machine it means that existing a one to one relationship between a machine and operations of a job, we have used a fitness function that satisfied the condition. The fitness function is obtained from (2). To assure this assumption, we should define a penalty coefficient that applies to fitness function ( FF 1 ). Fitness function is defined by (2):

FF^ = Ey₌₁min(£T) + FL (2)

where j is the number of jobs, FL is penalty coefficient and ET is the execution time of jobs. If two machines implement an operation of jobs simultaneously, penalty coefficient caused increasing FF₁ and the solution will be disregarded by COA.

Assign machines to operations based on the input sequence: After calculating the execution time of jobs and finding an optimal sequence of jobs on machines, turn is the allocation machines based on the input sequence. A sequence of jobs that the user will require determines which job to which machine should be delivered. We use operation-based presentation to allocate operation to machines [20]. Since each job exactly run on each machine once, in this way, the number of jobs exactly appears to the number of machine.

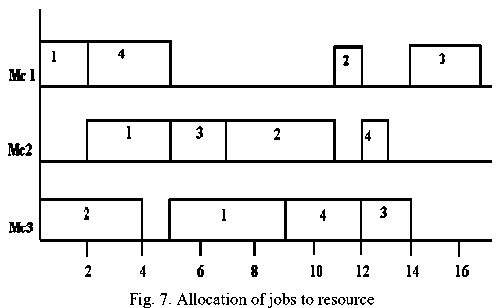
For example, Fig. 5 shows a sequence of jobs. Consider the problem with 4 jobs and 3 resources. Table 1 shows order of allocation of jobs to machines, and require time for executing on each machine.

Each number in this sequence shows the number of jobs. Since each job consists of 3 operations, each job exactly appears 3 times in each sequence. The first number is observed; number 1 that is the first appearance in this sequence indicates the first operation of job 1 and by referring in Table 1 executed in machine 1. Next number is 1 that is the Second appearance in this sequence so, it's indicate to second operation of job 1, by referring in Table 1 selected machine 2. Similarly, the sequence continues until the final sequence gets the machine of each operation. For this example, in the end Fig. 6 shows the sequence of machines. In addition, Fig.7 shows the allocation of jobs to 3 resources.

1

1

2

4

3

1

4

2

3

2

4

3

Fig. 5. A sequence of jobs

1

2

3

1

2

3

3

2

3

1

2

1

Fig 6. A sequence of resources

Table I. Allocate jobs to resource with execution time

Job	Machine and time of operation 1 (machine/time)	Machine and time of operation 2 (machine/time)	Machine and time of operation 3 (machine/time)
1	1/2	2/3	3/4
2	3/4	2/4	1/1
3	2/2	3/2	1/3
4	1/3	3/3	2/1

Table II: Parameter settings of PSO and GA algorithms

Algorithm	Parameter description	Parameter Value
PSO	Self-recognition coefficient c1	2
	Social coefficient c2	2
	Weight w	0.9     0.4
	Max Velocity	0.01
GA	Probability of crossover	0.5
	Probability of mutation	0.2

Calculate idle time of machines: Since the machines may be idle during run time, idle time calculating machines is important. The aim is minimizing the maximum execution time of machines. To ensure the assumption that two machines not be allocate to an operation at the same time, we define a fitness function to prevent the occurrence of this event. Fitness function is computed by the (3):

FF₂ = max (FT) + FL        (3)

Terminating Conditions: The algorithm terminates when an optimal solution gains or the maximum number of algorithm iterations has been reached.

• VIII.    Experimental results

The CUGA algorithm was implemented using Matlab software running under the Win XP operating system on a 1.66GHZ CPU with 2GB RAM. In our proposed algorithm, we assumed that the crossover rate is 0.5 and the mutation rate is 0.2.

Our proposed algorithm, solve the scheduling problem for several different states and the parameters of frequency have been studied. The average number of iterations for the algorithm to achieve the optimal solution and the average time spent in the system are presented in tables and figures. Because of the fact that our proposed algorithm depends on the input parameters, to change the input values and the output of scheduling algorithm will be change.

We have considered a finite number of small-scale processors in the grid environment. Each experiment has been repeated 10 times and the completion time values of best solutions in optimization iterations have been recorded. Afterward the minimum time of all the jobs has been calculated. Penalty coefficient in (2) and (3) is considered 1e2. If we ignore penalty coefficient, it will cause increasing in FF1 and FF2 and its condition is not considered by COA. CUGA has been compared with PSO [8] and GA [21] algorithms based on the execution time. The parameter settings of PSO and GA algorithms are presented in Table 2 and the results are shown in Table 3 and Fig. 8. We can observe in Table 3, by increasing the number of jobs, CUGA algorithm has less execution time than the other algorithms. Table 3 shows the average execution time of algorithms CUGA, GA and PSO for various iterations. For example, when maximum iterations is 50, the average running time of the CUGA algorithm in the grid environment with 4 jobs and 3 resources are equal to 14.6 seconds, at the same situation, for GA algorithm this time is 19.3 seconds and applying PSO the spent time is 18.2 seconds. The results show that our proposed algorithm does significant improvement in grid scheduling environment compared to other algorithms.

• IX.    Conclusion and future works

In this paper, we proposed algorithm to solve job scheduling problem in grid computing. This algorithm profits the advantages of cuckoo optimization algorithm and genetic algorithm. To satisfy the user requirements, CUGA selects the best resource and compute the minimum time for jobs execution on machines. In this paper, in order to show the efficiency of the proposed algorithm in terms of execution time, a comparison were performed employing CUGA algorithm and some other algorithms such as GA and PSO. Comparative results show that CUGA can considerably reduce timeconsuming required to achieve an optimal solution.

Table III: Comparison of the execution time (sec) between CUGA, GA and PSO algorithms

Number of jobs	Max Iterations	Number of machines	CUGA algorithm	GA algorithm	PSO algorithm
4	50	3	14	15	14
5			19	23	22
6			20	25	23
10			32	45	39
15			45	55	50

Table IV: Average running time (sec) of algorithms for different number of iterations

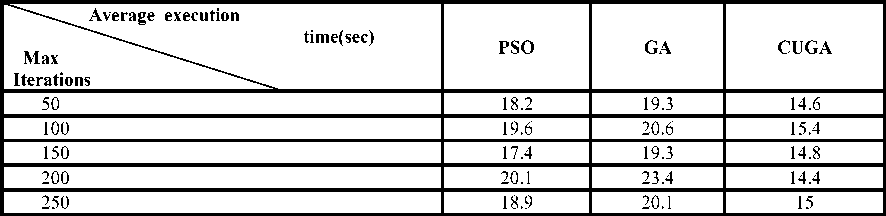
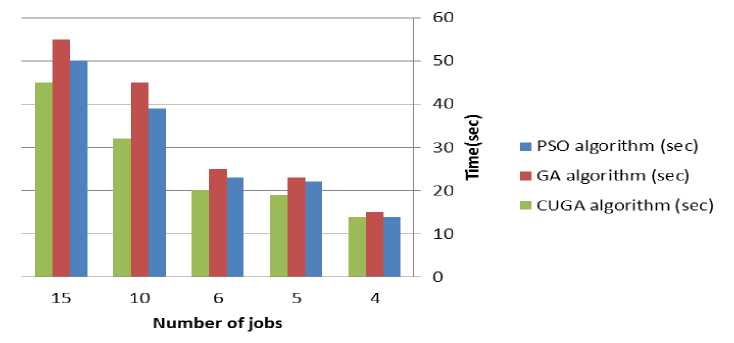
Fig. 8. Comparison of CUGA with GA and PSO, by increasing the number of jobs, the difference of spending times is obvious.

Acknowledgment

The authors gratefully acknowledge use of the services and facilities of University of Tehran. This work was supported in part by a grant from University of Tehran (No. 390835/1/01).