A Method of Hash Join in the DAS Model

Published Online February 2011 in MECS

Database outsourcing [1], [2] is becoming increasingly popular introducing a new paradigm, called database-as-a-service(DAS), where the data owner (DO) delegates her data to the database service provider (DSP), and users query on the external database. Since the server is powerful in procession of computational and storage resources, it can alleviates the workload of the data owner greatly. However, once the data is not stored in locations beyond the data owner’s control and accessed by an external database service, the results of query is required to be proved correctness.

Previous authentication techniques deal with range queries on a single relation using the data owner’s signature and the client’s verification of signature. On the other hand, few researches concern about join processing between multiple relations, which is a basic function for database manipulation, because authenticated join processing is inherently more complex since the combination of base relations are not signed by the data owner. A trivial solution is to send all tuples of participated relations to client, who verifies respective relations and computes join results. Obviously, it’s inefficient that the workload of join processing is shifted to client without taking full advantage of database service provider. Reference [3] is the first comprehensive work on sort-based join algorithms, which motives us to develop authenticated join algorithm based on other paradigms. For equi-join queries, a better alternative can

^∗ This work is supported by the National Natural Science Foundation of China under Grants 60773175, 60973134 and 70 971043, the Foundation of National Laboratory for Modern Co mmunications under Grant 9140C1108020906 ， and the Natura l Science Foundation of Guangdong Province under Grants 103 51806001000000 and 9151064201000058

be based on the hash join. This paper proposes a method of hash join in DAS model. To each relation, the data owner computes hash function and performs signature on a group of tuples with the same hash values. Hereafter, data and additional information including hash value and signature are outsourced to the DSP. When the client issues a query, the DSP generates an approximate join results based on pre-computed hash values and the verification object (VO), which are send back to the client for verification. If all tuples are successful to pass through verification, correct query results are finally picked out by evaluation the initial predicate. This paper analyzes the proof of soundness and completeness. We also experimentally demonstrate that proposed method has efficient performance under some metrics and effectively shift the workload to outsourcing database service.

The rest of the paper is organized as follows. Section 2 provides a background on cryptographic primitives. Section 3 surveys related work on authenticated query processing. Section 4 describes our technique HADO. Section 5 contains an experimental evaluation and Section 6 concludes the paper.

• II.    P RIMITIVES

In this section, we review some cryptographic essentials.

• A.    Hash Function

There are different definitions about hash function in cryptology and database community, respectively. We will describe it more clearly as follows:

In cryptology community, a hash function H maps a message m of arbitrary size to a fixed-length bit vector H(m). The collision-resistance property guarantees that it is computational infeasible to find two different message that map into the same hash value. Additionally, a desirable property is that H(m) is fast to compute. The most commonly used hash function is SHA1with an 160-bit output. We refer to H(m) as the hash value of m.

In database community, a hash function is used to construct a hash table that is useful as an index. A hash function H that takes a search key(the hash key) as an argument and computes from it an integer in the range 0 to B-1, where B is the number of buckets. If a record has search key K, then we store the record by linking it to the bucket list for the bucket number H(K).

In order not to cause confusion, a cryptographic hash is denoted as hash c , while a hash function to construct a hash table in database is denoted as hash d .

• B.    Aggregate Signature

  The concept of aggregate signature was introduced by Boneh, Gentry, Lynn and Shacham at Eurocrypt 2003. An aggregate signature scheme[4] is a digest signature that supports aggregation: given k signatures on k distinct messages from k different users it is possible to aggregate all these signatures into a single short signature. This useful primitive allow to drastically reducing the size of public-key certificates, thereby saving storage and transmission bandwidth. In this paper, a few of signatures of approximate join results are aggregated as a smaller set of short signature on DSP and then sent to client to be verified together with join results. It is very effective for client with limit storage and computation resources.

• C.    Merkle Hash Tree

The Merkle hash tree[5] is a method for authenticating a set of messages (e.g. data tuples) collectively, without signing each one individually. It is a binary tree over the digests of the messages, where each internal node equals the hash of concatenation of its two children. The owner signs the root of the tree with her private key. Given a message and the sibling hashes to the path in MHT from the root to the message, one may verify its authenticity by reconstructing bottom-up the root digest of MHT, and checking whether it matches the owner’s signature. The collision-resistance of the hash function hash c guarantees that an adversary cannot modify any message in a way that leads to an identical root digest.

Sroot-Sig(hi234)

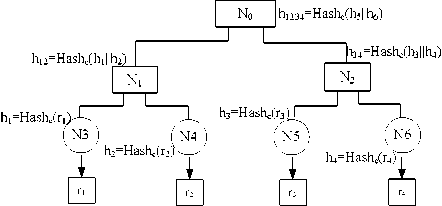
Figure 1. Example of MH tree

Figure 1 illustrates a simple range query. N3-N6 are leaf nodes containing the digests of all tuples; N1-N2 store hash values computed on the concatenation of N3-N4 and N5-N6; N0 is the root of MH tree which stores the hash values of the concatenation of N1-N2 and its signature using the secret key. Suppose the set of query results is {r2}, the DSP first expands it to include two boundary records r 1 and r 3 , which ensure completeness, and processes it using the MHT. The client can recompute the digest of the root and verify its signature by the verification object VO generated by DSP is {r 1 ,r 2 ,r 3 ,h 4 ,S root }.

Currently, the state-of-the-art ADS is the Merkle B-tree(MB-tree)[6], which combines the MHT with B+ Tree, i.e., it can be thought of as a MHT where the node fanout is determined by the block size. Reference[7]

propose Partially Materialized Digest scheme(PMD), which uses separate indexes for the data and for their associate verification information, and only partially materializes the latter. In contrast with previous work, PMD avoids unnecessary costs when processing queries that do not request verification, achieving better performance.

• III.    P ELATED W ORK

A. General Query Processing

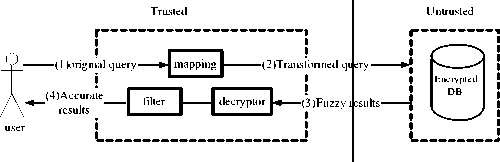
Figure 2. Query Processing in Outsourced Database

As a consequence toward outsourcing, highly sensitive data are now stored on systems run in locations that are not under the data owner’s control, such as leased space and untrusted partners’ sites. Therefore, data confidentiality and even integrity can be put at risk by outsourcing data storage and management. A promising direction towards prevention of unauthorized access to outsourced data is represented by encryption[8][9][10][11][12][13][14][15][16] [17]. However, in this paper our work focus on the data integrity while the data is still in plaintext. In outsourced database as illustrated in Figure 2, each query(1) is mapped onto a corresponding query (2) based on certain index technology and executed in that form at the untrusted server. The untrusted server returns the fuzzy result(3), which is then filtered by the trusted front. If indexing information is not exact, an additional query(4) may need to be executed to eliminate spurious tuples that do not belong to the result set.

• B.    Authenticated Range Processing

Existing verification methods for outsourced database follow two paradigms. The first is signature chaining. Assuming that the data are ordered according to search attribute A, the owner hashes and sign very triple of consecutive tuples. Given a range query on A, the DSP returns the qualifying data, along with the hashes of the first tuple to the left and the first tuple to the right of the range. It then includes the corresponding aggregate signature of the consecutive tuples in the VO. The client inspects the results by verifying the signature. Signature chaining approaches are shown to be inefficient because generating the signatures for each tuple incurs high computation cost of the owner. The described method in this paper computes the signature for each group of tuples instead of for a single tuple, which can reduce the cost of the data owner drastically. The second paradigm utilizes an MHT for result verification. We have introduced this method earlier and omit it here.

• C.    Authenticated Join Processing

[18]proposes the pre-computation and storage of all possible join results in materialized view, which imposes a significant overhead for the owner to construct and update a large number of materialized views. Moreover, it is infeasible to determine all possible join in advance in practical applications. [4] and [19] introduce a method called Authenticated Index Nested Loop(AINL) that is based on the index nested loop method. Y.Yany [3] firstly constructs authenticated join processing in outsourced database depending on authenticated data structure(ADS, i.e., MB tree) availability and proposes three novel join algorithms: (i) Authenticated Indexed Sort Merge Join(AISM) utilizing a single ADS on the join attribute for the inner relation. The DSP first sorts the outer relation to generate the corresponding rank list, whose purpose is to inform the client on how to restore the verifiable order of the records, and then transmits all tuples of the outer relation to the client in their verifiable order along with the owner’s signature. Next, the DSP turns to the inner relation to process authenticated range query by ADS and the no-go-back policy during the tree traversal. (ii) Authenticated Index Merge Join (AIM) that requires an ADS(on join attribute) for both relations. AIM improves the performance of AISM because AISM requires the DSP to sort all tuples for the outer relation and the client to verify and re-order them, whereas AIM only incurs one traversal of ADS for the outer relation and one hash computation for the client. (iii) Authenticated Sort Merge Join (ASM) that does not rely on any ADS. The DSP performs a sort-merge join and generates a VO such that the client can efficiently reconstruct the join output. Compared with AISM and AIM, ASM is naturally less efficient compensated by its flexibility, which is an important property for authenticating complex queries.

• IV.  T HE H ADO A PPROACH

Table 1 summarizes the primary symbols along with their interpretation used in the description of the HADO approach.

TABLE I.     P RIMARY SYMBOLS

Symbol	Description
|Sig|	Size of signature
|R|,|S|	Number of tuples in R,S
|Tup R |,|Tup S |	Size of tuple in R, S
B	Block size
e R ,e S	The percentage of filtered tuples in all tuples of R, S
B x , sig_B x	The block of id x and its signature
Agg_sig	The function of aggregate signature
C I/O	Cost of I/O
C agg_sig, C agg_verify	Cost of aggregate signature, verification

• A.    Algorithm Description

Based on the general query Q=σ p (R∞S), the following steps 1-3 are the pre-prepared tasks and steps 4-10 describe actual join processing.

• 1.    The DO computes hash d functions on join attributes of R and S. Ideally, an appropriate hash d function produces the uniform distributed of R or S.

• 2.    Without changing the existing storage structure, a system table for each relation is created on the DSP to store hash values, which contains three attributes: the bucket id, the collection of ids within the bucket and a signature of all tuples in the bucket.

• 3.    The DO generates MB trees for some attributes and stores them on the DSP. We consider p characterized by the following grammar rules: (1) Condition 1←Attribute op Values; (2)Condition 2←Attribute = Attribute; (3)Condition

• 4.    Given a query, the DSP divides p(i.e., condition 3) into corresponding conditions on a single table (i.e., condition 1) which is denoted as p 1 , and corresponding join conditions on multiple tables (i.e., condition 2), which is denoted as p 2 . This division function is called DIV(p)= p 1 U p ₂ . Once we know how conditions are divided, we will be ready to discuss how query is translated over the server-side implementation.

• 5.    If p 1 involves n attributes, the DSP executes n auth _’ enticated range queries on n MH trees to generate VO i (i=1..n), which is inserted into the VO, and computes all bucket ids that range query results belong to.

• 6.    The realization of the combination of p 1 (i.e., condition 3) depends on the logical correlation yet. If the logical operator is “AND”, the results are the intersection of respective bucket sets. If the logical operator is “OR”, the results are the union of respective bucket sets.

• 7.    Based on the temporary set of bucket ids resulting from step 6, the DSP performs hash join according to p 2 . The reason why we retain all tuples in the appropriate bucket ids is that we can apply aggregate signature to these buckets and provide verification for client. What about the incorrect tuples in the temporary set? The DSP can generate the bitmap of M R or M S for R or S. Let t is the order of a record r G R in the bucket, usually which is in accordance with the order of the primary key. If r is marked, M R [t] is set to 1; otherwise (r is out of range query results), M R [t] is set to 0. The bitmap M s is generated in the same way and appended to the VO.

• 8.    Suppose the set of buckets of results are {B a1 , B a2 ,…, B ai } for R and {B b1 , B b2 ,…,B bj } for S, the two aggregate signatures Sig ^R and Sig ^S for R and S are computed by the DSP: Sig ^R = Agg_Sig{sig_B a1 ,sig_B a2 ,…,sig_B ai }; Sig ^S = Agg_Sig{sig_B b1 ,sig_B b2 , …,sig_B bj } and the final VO i ncludes:VO={B a1 ,B a2 ,…,B ai , B b1 ,B b2 ,…,B bj ,Sig ^R ,Sig ^S , V O 1 ’, VO 2 ’,… VO n ’,M R ,M S }

• 9.    Upon obtaining the VO, the client computes and verifies the results in two steps. Firstly, the client uses VO 1 ’,VO 2 ’,…, VO n ’ to verify range query on individual relation. Secondly, the set of buckets for R and S are verified by the Sig ^R and Sig ^S . If VO doesn’t pass the two steps, either the results of rang query on individual relation are incorrect or the tuples to participate in join processing are modified without authorization, hence the

• 10.    The client produces matching join pairs locally on the bucket of R and S with the same bucket id. Because there exist tuples in the same bucket id of R and S without matching each other yet, the client needs to execute the join condition to get the final results. Meanwhile, the client verifies the correctness of the bitmap, i.e., records marked “0” must not participate in any join results. Note that the usage of the bitmap reduces the I/O operations.

3^(Condition v Condition)|(Condition л Condition)|( ^ Cond- ition))

query process is stopped; otherwise, it continues to compute join results.

• B.    An Example

  In the example, we use the database of Figure. 3. Given Q1⁼π cid,did (σ addr=’River’ and amount>3000 (Customer^∞Deposit)); Q2⁼π cid,did (σ addr=’River’ or amount>3000 (Customer∞Deposit)).

cid	cname	tel	addr
c1	Tom	3450	New York
c2	Mary	2854	River
c3	John	9432	Main
c4	Jerry	6130	River
c5	Susan	7650	London
c6	Smith	7692	Tokyo

(a)

did	amount	cid
d1	2000	c2
d2	300	c6
d3	2500	c3
d4	10000	c4
d5	5780	c4
d6	2600	c1
d7	120	c3
d8	4600	c5
d9	1800	c1
d10	6300	c6

(b)

Figure 3. The Relation (a)Customer and (b) Deposit

In the preparation, the DO computes the same hash d functions on the same attribute cid of Customer and Deposit. The corresponding hash system tables are created displayed in Figure 4. (a) and (b).

gid	ids	sig
0	c1,c3	11011011…
1	c2,c4	10101101…
2	c5,c6	11101100…

gid	ids	sig
0	d3,d6,d7,d9	10000011…
1	d1,d4,d5	11000111…
2	d2,d8,d10	10100001…

(a)                                       (b)

Figure 4. The hash system table of (a) Customer and (b) Deposit

Given Q1, the DSP divides p into p1 and p2: p1= (Customer.addr=”River”) ∧ (Deposit.amount>3000); p2= (Customer.cid=Deposit.cid). Firstly, the DSP performs authenticated rang queries according to p1. During the traversal, VOaddr and VOamount are created into the VO: VOCustomer.addr={hA,c1,c2,c4,c6,Sigaddr}; VODeposit.amount={hF,hd3, d6,d8,d5,d10,d4,Sigamount}. The results (c2 and c4) of range query on Customer.addr are in the bucket id 1; the results (d8,d5,d10 and d4) of range query on Deposit.amount are in the bucket id 1 and 2. The implementation of p1 is the combination of the two set of results. Because the logical operator is “AND”, the final bucket id is 1. Next, the DSP computes join operation between B1Customer and B1Deposit.( is denoted as a tuple whose primary key is x): B1Customer={,}; B1Deposit={,,}. In this example, the aggregation of signatures can be omitted because of only one bucket id 1. The signatures of bucket id 1 (Sig1Customer and Sig1Deposit) are inserted into the VO. We will see later in an example of Q2, aggregation of signatures is very useful. Note that using the bitmaps to improve the performance, MCustomer={(1,1)}and MDeposit={(0,1,1)}, since Deposit d1

Root _addr

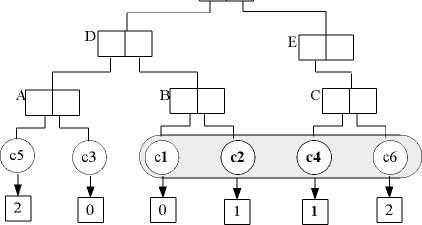
(a)

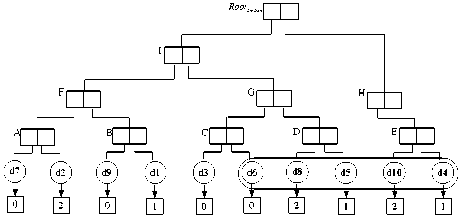
(b)

does not satisfy p1. M Customer and M Deposit are inserted into the VO. So the final VO is VO={ B 1^Customer , B 1^Deposit , Sig 1^Customer , Sig 1^Deposit , VO Customer.addr , VO Deposit.amount , M Customer , M Deposit }.After receiving the VO, the client is required to verify (1) the correctness of VO Customer.addr and VO Deposit.amount ; (2) the correctness of B 1^Customer and B 1^Deposit by Sig 1^Customer and Sig 1^Deposit , respectively; and (3) the correctness of M Customer and M Deposit . If the verification is successful, the hash join results are generated: {, }; otherwise the query is terminated.

Given Q2, the whole process is similar. Note that the logical operator is “OR”, the final bucket ids are 1 and 2. The DSP computes join respectively on {B1Customer, B1Deposit} and { B2Customer, B2Deposit }. B1Customer and B1Deposit are the same as above. B2Customer and B2Deposit are described below: B2Customer={,}; B2Deposit={,,}. The DSP aggregates signatures of two buckets to generate only one as follows: SigAggCustomer=Agg_Sig{Sig1Customer, Sig2Customer}; SigAggDeposit=Agg_Sig{ Sig1Deposit, Sig2Deposit }. The bitmap of Customer and Deposit are MCustomer={(1,1),(1,1)}, MDeposit={(1,1,1),(0,1,1)}, since Deposit d2 is certain not to take part in the join operation. So the final VO is VO={ B Customer B Deposit B Customer B Deposit Sig Customer SigAgg , VOCustomer.addr, VODeposit.amount, MCustomer, MDeposit}

• C.    Proof of consistency

Proof of soundness: Suppose that the DSP deceives the client into generating a wrong results . Then either (i) r does not match s, or (ii) r or s is unauthorized modified. The first case is impossible as the client generates matching pairs locally. Case (ii) is detected by the authenticated information of R and S.

Proof of completeness: Let be a valid result of the query missed by the client. Then either (i) the client does not receive r or s, or (ii) the client does not identify r and s as a matching pair. For case (i), if r is absent from the VO, (1) r is missed in the range query on single relation. For the client to correctly construct h root by MH tree, the VO must contain the digest of r or a node covering r. For instance, if Customer c2 is omitted, it is impossible to compute correctly h Customer.addr to match its corresponding signature. (2) r is missed in the process of conjunction of simple conditions. Aggregate signatures can ensure all tuples of buckets in VO. For instance, if Deposit d1 is omitted, it is impossible to verify Sig Agg^Deposit . Therefore, the first case is impossible. For case (ii), (1) the DSP provides the wrong bitmap of R or S, which can be detected during the verification of the bitmap of R or S (i.e., sets the bitmap to 0, although the tuple can be joined) since all possible tuples have been in the VO. (2) the client deals with r and s in a wrong way. It is impossible for the client to do incorrect computation locally.

• D.    Performance analysis

Query processing and VO creation cost: Query processing cost at the server breaks into I/O cost for tuples, as well as CPU time to build the VO for range queries by MH trees and aggregation signatures:

I R I *IM * e . I ^ *1 TuPs\ * e s Y_{c +} 1 B| ⁺ B J C I / O ⁺ 2 C agg _ sig

n

У c +

VO_i _ creation

i

^

Communication cost: The VO size is the main metric of the cost of communication. It mainly includes the size of VOs by MH trees, the size of all possible tuples and signatures.

n

| R | * TUP r | * e ^ + | S | * T«P s | * e s + 2 | VO i | + 2 * | Sig| i = 1

Computation overhead of the client: Given the VO, the client has to verify n VOs by n MH trees and aggregate signatures before executing hash join.

y_{r +9} _ J 3* (I R I *1 TupA * e « + S I * TuP s I* e s ) Y

2-^ C VO ' _ verify ⁺ 2 C^a SS ^_ verify ⁺l                       B                      I C l / ^O

• V.    E XPERIMENTAL E VALUATION

  In this section, we experimentally evaluate the performance of our method. The experiments are conducted on two Lenovo personal computers with Interl Core 2 Quad CPU Q9400 2.66GHz and 1.83GB RAM. One of the computers performs as the server, and another one performs as the client according to our client/server architecture. Relevant software component used are Oracle 9i and Microsoft Windows XP as the operation system. We use two tables R(r1,r2,r3) and S(s1,s2,r1)

with uniformly distributed key, where the primary keys of R and S are r1 and s1. In addition, S.r1 is a foreign key that reference R.r1. MH trees are constructed on the attribute r2 and s2 respectively before query processing. The parameters in our simulations are the query selectivity Q and the tuple size T. The number of tuples in R and S is 2500 and 10 ⁶ . Q varies 1% to 50% with the default Q of R and S is 20% and 1%. The default T is 64. In each experiment, we vary a single parameter and set the remaining ones to default values compared with AINL[4][19] and AIM[3]. The SQL queries in these experiments are shown belown:

Q1⁼σ R.r2(R ^∞ S) Q2⁼σR.r2(R ^∞ S)

In the first set of experiments, we study the size ratio between VO and database size, named as the ratio of VO in short. Figure 6 shows that the ratio of VO size, which is clearly dominated by the query selectivity because the tuples out of results have rapidly increased and more unnecessary tuples take part in join processing. This disadvantage becomes more obvious with the growth of query selectivity so a threshold is usually set to limit the running of the algorithm. Figure 7 depicts the VO size of Q1 and Q2 and demonstrates VO size is sensitive to the query conditions. The reason is that different query conditions lead to the different number of hash buckets, which directly affect the VO size. Compared with AINL and AIM as showed in Figure 8, when most tuples are filtered out, the cost of communication is optimized due to that a small part of tuples are selected to be joined and verified.

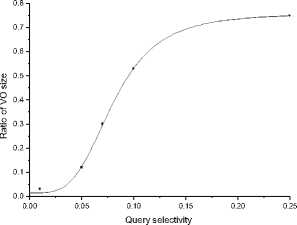
Figure 6. Ratio of VO size with different query selectivity

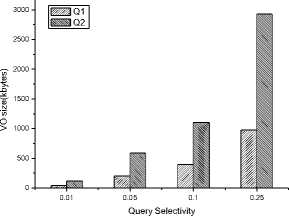
Figure 7 VO size of Q1 and Q2 with different query selectivity

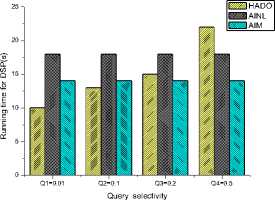
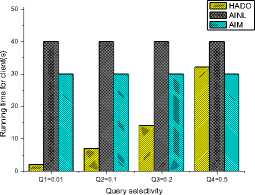
In the second set of experiments, we focus on the running time of the DSP and client. Figure 9(a) and (b)

study the effect of query selectivity on the querying processing time of the

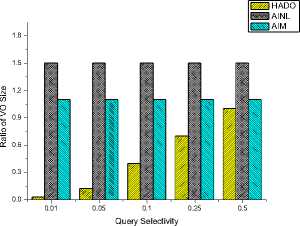
Figure 8. Comparison of the ratio of VO size

(a)

(b)

Figure 9. Comparisons on the running time of DSP and Client with different query selectivity (a)Running time for DSP (b)Running time for Client

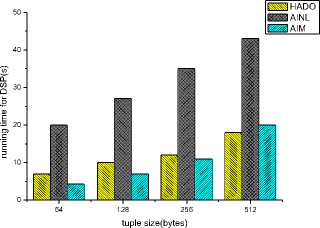
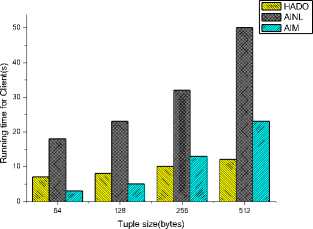
DSP and the Client. With the growth of query selectivity, the cost of aggregate signature increases by the DSP leading to processing more buckets by the client and then increasing the running time of the DSP and the client. However, since AINL and AIM deal with all tuples so the variation is small. Next, we fix the query selectivity and vary the tuple size. In [3], AISM is sensitive to the tuple size because the sort-based join algorithm has a size requirement that depends on the sum of the argument sizes (B(R), B(S)) rather than on the smaller of two arguments sizes that hash-based algorithm requires. In Figure 10, we observe that with the increase of tuple size, the variation of the running time of the DSP and the client in HADO is smaller than that in AINL and AIM.

(a)

(b)

Figure 10. Comparisons on the running time of DSP and Client with different sizes of tuples (a)Running time for DSP (b)Running time for Client

• VI.    D ISCUSSION

The core technique of HADO is to pre-compute some query conditions by MH trees and to authenticate the tuples to participate in join by aggregate signatures. We should consider the following situations when applying the HADO algorithm:

• (i)    The query selectivity. When the query selectivity is larger, more hash buckets are selected in the VO and then HADO may become a worse method because the additional computation of aggregate signature increases the burden of DSP.

• (ii)    The frequency of data update. In the preparation of joining, the DO should pre-compute hash d functions, which is generated according to the distribution of the newest version of outsourced data. If the data is updated frequently, the hash d functions may be a “bad” one to reduce the efficiency of query, which leads to reconstruct hash d functions and upload them to the outsourced database again.

• (iii)    Security. The Security of HADO is to resist tampers of malicious server to modify data without being detected, which is a component of security of outsourced database [20][21]. However, the data confidentiality is lost because the outsourced data is still in plaintext and the query privacy is also out of consideration. Therefore, privacy-preserving query on the encrypted outsourced database is the next direction of future works.