A Modified Particle Swarm Optimization Algorithm based on Self-Adaptive Acceleration Constants

Published Online August 2017 in MECS DOI: 10.5815/ijmecs.2017.08.07

Metaheuristic optimization techniques have become very popular over the last two decades [21]. They have been mostly inspired by very simple concepts. The inspirations are typically related to physical phenomena, animals’ behaviors, or evolutionary concepts.

Regardless of the differences between the metaheuristics, a common feature is the division of the search process into two phases: exploration and exploitation. The exploration phase refers to the process of investigating the promising area(s) of the search space as broadly as possible. An algorithm needs to have stochastic operators to randomly and globally search the search space in order to support this phase. However, exploitation refers to the local search capability around the promising regions obtained in them exploration phase. Finding a proper balance between these two phases is considered a challenging task due to the stochastic nature of meta-heuristics.

There is a question here as to why metaheuristics have become remarkably common. The answer to this question can be summarized into four main reasons: simplicity, flexibility, derivation- free mechanism, and local optima avoidance.

First, metaheuristics are fairly simple. The simplicity allows computer scientists to simulate different natural concepts, propose new meta-heuristics, hybridize two or more metaheuristics, or improve the current metaheuristics.

Second, flexibility refers to the applicability of metaheuristics to different problems without any special changes in the structure of the algorithm assuming problems as black boxes. So, all a designer needs is to know how to represent his/her problem for metaheuristics.

Third, the majority of meta-heuristics have derivation-free mechanisms i.e. meta-heuristics optimize problems stochastically. The optimization process starts with random solution(s), and there is no need to calculate the derivative of search spaces to find the optimum. This makes meta-heuristics highly suitable for real problems with expensive or unknown derivative information.

Finally, meta-heuristics have superior abilities to avoid local optima compared to conventional optimization techniques. This is due to the stochastic nature of metaheuristics which allow them to avoid stagnation in local solutions and search the entire search space extensively.

One of the interesting branches of the population-based metaheuristics is Swarm Intelligence (SI). The inspirations of SI techniques originate mostly from natural colonies, flock, herds, and schools. Here, the search agents navigate using the simulated collective and social intelligence of creatures. Some of the most popular SI techniques are Particle Swarm Optimization (PSO) [1], Ant Colony Optimization (ACO) [22], Artificial Bee Colony (ABC) [23] and Bat Algorithm (BA) [24] etc.

Among these, Particle Swarm Optimization (PSO) is one of the most efficient optimization strategies for continuous nonlinear optimization problems. J. Kennedy et al. [1] first proposed PSO that is inspired by the collective social behaviors of swarm like movements of flocks of birds or schools of fish in search of foods. The main advantages of PSO are that PSO is very simple and efficient in nature (no need of gradient of the problem etc.); there are few parameters (no need of different complex genetic operators etc.) needed to be adjusted. In addition to the huge number of theoretical works, PSO has been applied in various fields of study DC-Side Voltage Control [25], Task Scheduling [26], Workflow Scheduling [27] and Transportation Network design [28] problems etc.

In case of PSO, a particle (i.e. bird or fish) denotes a potential solution for the optimization problem. A set of particles is known as a swarm, where particles are initially distributed or positioned in random manner in d -dimensional search space of the problem. Swarm is flown through the search space and the position of each particle is updated based on the experiences (fitness value at that point) of all neighbors particle including itself [2]. Every particle is considered as intelligent and knows its own current fitness value, its own best value so far (locally best solution), the best fitness value of the whole swarm (globally best solution), and its own velocity [3].

For, d -dimensional optimization problem, the position of i -th particle of a swarm (consist of N particles) at t -th iteration is given as X f _d = (x^x^,.... ,x d and the velocity is represented by V;^ = (v /1 , V /2 , ^., V / _d) . Locally best solution by i -th particle at current iteration is given as ^p bestM = ^(p i1 -^p i2 >™->^p id) ^and global ^best solution is denoted by G b _est , _d = (G 1 , G 2 ,...., G_d) . As iteration proceeds, the velocity and position of the particles are updated according to following rules [1].

^+1 = ^Vu + ^C 1 * rand(1, d) О ^(pt _b est^d - 4J +C 2 *rand(1,d)O(GU ,d -^ td ) (1)

^5¹ = V /td ⁺¹ + ^ itd (2)

Where C 1 and C₂ are called as acceleration constants, also named as cognitive learning rate and social learning rate respectively. rand(1, d) is generate a d -dimensional array of random values within [0,1]. О denotes element wise multiplication.

However, one of the main reasons behind the success of a metaheuristic is a delicate balance between exploration and exploitation capability of the algorithm. Several authors [4-18] proposed different methods to achieve better accuracy and convergence. However, in this paper, we have proposed a Modified Particle Swarm Optimization (MPSO) Algorithm based on self-adaptive acceleration constants. The rest of this paper is organized as follows. Section II describes different existing PSO strategies. The proposed Modified PSO is described Section III which is followed by results and analysis section. Next, conclusion and references are provided.

• II.    R elated W orks

To get a better control between the global and local search characteristics of PSO, Shi and Eberhart [4] proposed a modified PSO where the velocity of each particle is updated based on inertia weight (w). So, the velocity update rule is modified according to following equation.

• ^V;T = % *^wt + ^C i * ^rand(1, ^{d) O (p} b,est,l,d ^- ^d) +C 2 * rand(1, d) О (G best,d - X^) (3)

Recently, researchers give lots of attentions to the inertia weight parameter for improving the performance of original PSO. Lots of strategies were already proposed for updating inertia weight during the course of iteration.

In 1998, Shi and Eberhart [4] proposed Constant Inertia Weight (CIW) technique where they claimed that large constant value of Inertia Weight is suitable for exploration while a small constant value of Inertia Weight is suitable a exploitation. So, CIW can be described using following equation.

w^t = Constant (4)

Further, in case of Random Inertia Weight (RIW) [5], the value of inertia weight is selected in random manner and it is very efficient to find out the optima in a dynamic system. For RIW, the value of inertia weight is assigned using following equation wt = 0.5 + rand/2 (5)

Where rand is a function that generates random number within [0, 1]. Therefore, value of inertia weight is uniformly distributed over [0.5, 1] and this technique partially solve the problem of selection for constant of CIW.

Linear Decreasing Inertia Weight (LDIW) [6-8] is very popular and efficient technique in improving the finetuning characteristics of the PSO where the value of inertia weight is linearly depend on the iteration number. In case of LDIW, the value of w is linearly decreased from an initial large value (w _mnx ) to a final small value (w_m in ) according to the following equation:

t “max-^min'l w wmax I t } X t (6)

^L max

Where t is iteration index and t _max denotes maximum number of iteration. LDIW has better efficiency over the others technique due to smooth transition from initial global search to local search during iteration process [20].

There are lots of others strategies for variation of inertia weight like Adaptive Inertia Weight [9], Sigmoid Increasing Inertia Weight [10], Chaotic Inertia Weight [11], Oscillating Inertia Weight [12], Global-Local Best Inertia Weight [13], Simulated Annealing Inertia Weight [14], Exponent Decreasing Inertia [15], Natural Exponent Inertia Weight Strategy [16], Logarithm Decreasing Inertia Weight [17], Nonlinear Decreasing Variant of

Inertia Weight [18] and Bat-PSO hybridization [19] etc. However, in this context, our proposed technique is compared with only other 3 strategies which CIWPSO, RIWPSO and LDIWPSO for validation purpose

• III.    M ethodolody

Fine parametric tuning of evolutionary algorithms is very important aspect to improve accuracy and efficiency. Earlier approaches [6-8] were mainly focused on the variation of inertia weight to increase the efficiency of PSO. However, they normally used fixed acceleration constants C 1 and C 2 ( C 1 = C 2 = 2 for most cases') during the course of iteration.

In this work, instead of using fixed acceleration constants, a weight based acceleration variables C 1 _wP and C2^:_wGis proposed that depends on the current best particle solution and global best particle solution respectively. These variables are updated adapted themselves depending on difference between best and worst fitness value. The velocity update rule for modified PSO can be written as according to following equations

^V iT = V)-^ + ^C 1 _w p * ^rand(1,d) О ^(PB est,i,d -Х^) + CIwg * rand(1, d) О (GUm - Х ^д)     (7)

Where C 1 _wP and C ^ _wG are defined as following way

Гt

C1wP

Гt

C2wG

f(Pbest,l,d)  fWorst fitness^ -fitnessWorst

f(Gbest,d)  /Worst fBest-fWorst

Where f(Pbest,i,d) , f(Gbest,ci) are fitness values corresponding to the local best for i-th particle and global best solution respectively. fBest and fworst are the best and worst fitness for all particles in current iteration. For a function minimization problem, fBest and fworst are defined as follows fBest = Minimum fitness for Х^.ХЦ,........,Х^Д fworst = Maximum fitness for Х1^ d,Х2d,........, Х ^ d

The particles are moving to the optimal point based on above self adaptive mechanism. However, if all particles move to an optimal point during iteration, minimum and maximum fitness value will be same. In that case, C 1 _wP and C2^, _wG will be undefined. To avoid such case during iteration, we introduce a condition that when f B _est and f w _orst are different, C 1 _wP and C 2 _wG are updated according to equation 8 and 9 else C 1 _wP = C ^, _wG = 2 will be considered.

Moreover, wt is also updated according to LDIW technique i.e. equation 6. The pseudo code of Modified

Particle Swarm Optimization (MPSO) algorithm is given as

Start MPSO Algorithm

Define N, d, ^t max , ^Х тах , ^Х min , ^ max , ^ min ^and objective function;

for i=1 to N (number of particles)

Initialize Х_и and V_l4 ;

^P best,i,d = ^Х i,d ;

end;

Evaluate fitness value f(Х_i , _d)for all N particle position (i=1, 2,...., N);

G best,d = Min (f);

• Assign value of w^t according to LDIW [Equation 6];

While (t <  t _max )

for i=1 to N fBest = Min (f);

f Worst = Max (f);

Evaluate ^f(p b ^t est,i,d) , ^f(G best,d) ;

if (f Best * f Worst )

Calculate C 1 _wP and C 2 _wG using equation 8 and 9 respectively;

else

t „—ct

^C 1wP = ^C 2wG = 2;

end if;

Update the velocity V_i , _dusing equation 7;

Update the position Х _i , _d using equation 2;

Evaluate fitness value for f(Х _i , _d');

iff(Х i,d ) <  f(P lest,i,d)

P best,i,d =Х i,d ;

end if;

^{if f (P} best,i,d' ⁾< ^f(G best,d' ⁾

t         Pt

^G best,d      ^P best,i,d ^;

end if;

end for;

Х* = Gbestd end while;

Return Х * ;

End MPSO Algorithm

• IV.    E xperrimantal R esults

To validate the proposed MPSO algorithm, we have chosen 6 different benchmark functions which are Ackley, De Jong, Easom, Easom, Griewank, Rastrigin and Rosenbrock function respectively. All of these functions are multimodal except De Jong function (also known as square function) which is unimodal in nature. The details of these functions, respective search ranges of variables and corresponding global minima points are shown in table 2. We have considered 10 dimensional optimization problem ( d =10) for all functions.

• A.    Parameters Setting

In this work, CIWPSO, RIWPSO, LDIWPSO and proposed MPSO were applied for above mentioned function minimization problems. Performance of MPSO is also compared with others for validation purpose. For this, a swarm of 50 particles and 1000 maximum iteration was taken. Following table shows values of respective different inertia weight parameters and acceleration constants for different techniques. All the techniques were implanted using Matlab 7.6 with 2 GB RAM, Dual Core processor and Windows7 operating System.

• B.    Analysis of Results

In this research work, all techniques are executed for all benchmark functions and result analysis is done based on five different criteria i.e. best fitness, average fitness, worst fitness, average execution time and convergence speed.

As the performance of PSO is also depending on initialization of particles, therefore, each program for each function is simulated for 50 times with different initialization. The best and worst fitness is the minimum and maximum fitness value respectively among those 50 optimal outputs corresponding to 50 times run. Average fitness and execution time is the mean of all cases of output fitness and execution time respectively.

Table 3 shows a comparative study among different strategies for all six benchmark problems on the basis of best fitness, average fitness, worst fitness and average execution time where best values are shown in bold letter and worst values are denoted by inverted letter.

Next, we have observed the convergence of each algorithm for each of the functions. Followings figures depicts how the fitness value decreases with respect to iteration number for all strategies and functions.

From Table 3, it can be observed that proposed MPSO gives best fitness for all function except De Jong and Easom functions. Though the best fitness for De Jong is quite satisfactory, but MPSO underperformed for Easom function. MPSO has been stuck to a local minima point (/ „ =0) for Easom function. LDIWPSO performs better with respect to average fitness and worst fitness while CIWPSO is the fastest technique on the basis of average execution time. However, execution time of MPSO is slightly higher than others due to incorporation of self adaptive technique in the algorithm. Now, if we observe the convergence graph for different algorithm, we observed that MPSO converge faster than other methods for all functions except Easom. RIWPSO is the worst technique on the basis all performance parameters except average execution time.

Table 4 summarizes the output of this study where best and worst techniques for different parameters are mentioned. Best technique is selected on the basis of maximum voting for each parameter against all functions. However, best fitness and convergences are most important parameters for an optimization technique. It can be observed that MPSO is better technique on the basis of best fitness and convergence. So, MPSO is preferable than others technique such as LDIWPSO, CIWPSO and RIWPSO.

Table 1. Different Benchmark functions

Function name	Function			Range of search	Global minima point
Ackley	-20 exp	1*'	d - exp [—^ cos(2nxi)] + 20 + e	-30 < xi< 30	A= 0 at (0Д...0)
De Jong	d ь i-1			-5.12 < ^ < 5.12	A= 0 at (0Д...0)
Easom	d                   d (-1)d+1HcOS (% i ) exp [-^(X i -n)2] i-1                   i-1			-30 < xi< 30	/ , = -1 at (n, n,... ., n)
Griewank	d 1 V.      (У)+1 400 Zj i    W			-600 < ^ < 600	/ . = 0 at (0,0,_0)
Rastrigin	d 100d +^[x2 - 10 cos(2n% i )] i-1			-5.12 < x , < 5.12	/ . = 0 at (0,0,_0)
Rosenbrock	d-1 ^ [(% i - 1)2 + 100(% i+i - x2)2] i-i			—5 < % i < 5	f . = 0at(1,1,^,1)

Table 2. Optimization Parameters for different inertia

Techniques	Inertia Weight	Acceleration Constant
CIWPSO	ш1 = 0.5	c 1 = c2 = 2
RIWPSO	ш1 = 0.5 + rand/2	c 1 = c2 = 2
LDIWPSO	ш( = штах - { ш”"-ш ”-" 1 X t where штах = 0.9 and ym i„ = ‘max 0.4	c 1 = c2 = 2
MPSO	ш ‘ = штах - f " max Ш т,п } X t where штах = 0.9 and ymin = *-    ‘max    -* 0.4	Self-Adaptive [Eq. 8 and 9]

Table 3. Comparative study for different PSO algorithm

Algorithm	Function name	Ackley	De Jong	Easom	Griewank	Rastrigin	Rosenbrock
CIWPSO	Best fitness	4.44E-15	1.34E-58	-1	0.352708	0.994981	4.03E-05
RIWPSO		0.100554	0.421686	-0.99951	0.053163	11.29862	5.271942
LDIWPSO		1.64E-13	1.09E-28	-1	0.018774	1.000377	8.87E-05
MPSO		7.99E-15	1.32E-29	-4E-13	0.014455	2.13E-07	2.42E-05
CIWPSO	Average fitness	0.079133	1.26E-27	-1	2.25284	4.803865	6.403575
RIWPSO		3.631267	2.63E-05	-0.35416	0.762569	32.43858	109.912
LDIWPSO		0.000132	4.67E-13	-1	0.089828	4.826136	5.589858
MPSO		0.028382	7.84E-17	-8E-15	0.137153	8.121388	6.935556
CIWPSO	Worst fitness	1.646224	4.3E-26	-0.99996	11.59614	19.89914	96.85403
RIWPSO		13.11975	6.714779	-2E-21	4.920912	80.68314	681.5958
LDIWPSO		0.006591	2.34E-11	-1	0.366723	11.93968	28.53141
MPSO		1.155319	3.39E-15	-1.2E-87	0.50223	17.90925	82.39822
CIWPSO	Average Execution Time (Sec)	30.25599	10.38025	29.75094	29.65551	12.11045	11.20735
RIWPSO		30.56758	10.40836	30.12699	29.53889	12.38601	11.09225
LDIWPSO		30.5915	10.82977	28.99117	29.01396	12.636369	11.626796
MPSO		131.2823	71.70359	128.9571	131.992	85.586803	81.651894

Table 4. Performance Analysis of different algorithm

Performance Parameter	Best Techniques	Worst Technique
Best fitness	MPSO	RIWPSO
Average fitness	LDIWPSO	RIWPSO
Worst fitness	LDIWPSO	RIWPSO
Average Execution Time	CIWPSO	MPSO
Convergence	MPSO	RIWPSO

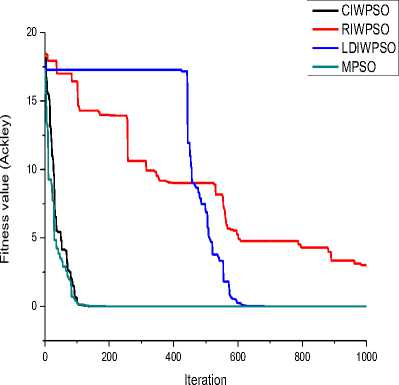
Fig.1. Convergence for Ackley function

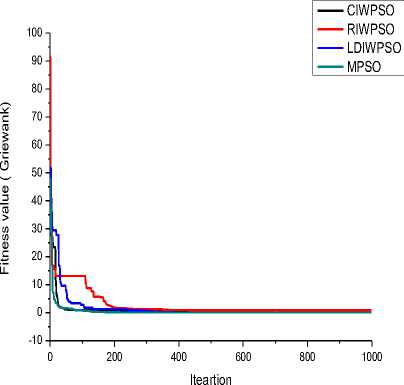
Fig.4. Convergence for Griewank function

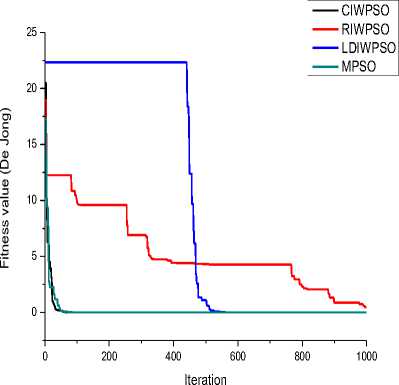
Fig.2. Convergence for De Jong function

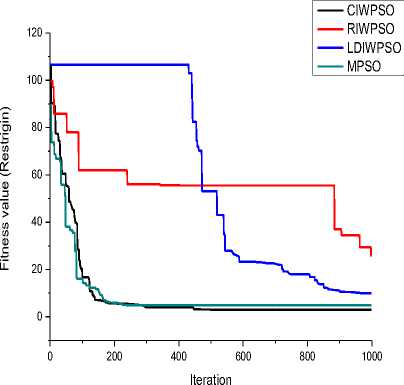
Fig.5. Convergence for Restrigin function

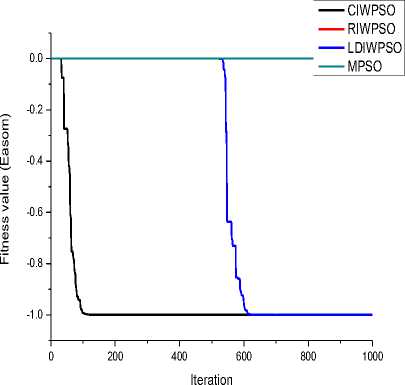
Fig.3. Convergence for Easom function

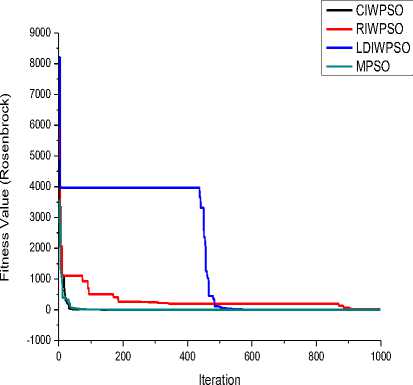
Fig.6. Convergence for Rosenbrock function

• V.    C onclusion

Several state of art techniques for inertia weight variation of PSO are already developed to increase the efficiency of PSO. However, in this paper, a Modified Particle Swarm Optimization Algorithm based on self-adaptive acceleration constants is proposed for further improvement in the accuracy of PSO. Here, acceleration constants depend on the global best particle solution and current best particle solution and updated themselves during the course of iteration. The proposed method is tested against six different benchmark functions. The results are also compared with other three strategies i.e. CIWPSO, RIWPSO and LDIWPSO. It is found that MPSO is most suitable for function optimization with best fitness value and convergence. However, its execution time is slightly higher than others technique. In future, different strategies for updating acceleration constants may be employed for further improvement of the performance of PSO.