A multi QoS genetic-based adaptive routing in wireless mesh networks with pareto solutions

Published Online September 2018 in MECS DOI: 10.5815/ijcnis.2018.09.01

The routing in multi-hop mobile networks has been considered one of the outstanding design matters, which significantly affects their attainable achievement. Subsequently, proficient routing methods ought to be intended for guaranteeing that the information packets proliferate in an "ideal" way regarding a few measures, for example, packet loss ratio, defer-jitter, delay, and bandwidth. All the preferred goals are improved all together in the conventional multi-hop mobile networks. However, in certain commonsense applications, to find the different solutions, each of which is ideal regarding an individual QoS measure might be superior to finding a solitary worthy arrangement, which incurs a balance among a few different variables [1]. A few Shortest Path (SP) search algorithms like Bellman-Ford and Dijkstra perform successfully for settled framework wireless or wired networks. In any case, they experience the ill effects of high computational complexities in networks with quickly changing topology as well as system status. Classically, SP routing problem has been formulated to combinatorial optimization that seeks to find the single best solution in one run. Routing in mobile networks involves simultaneous optimization of multiple QoS parameters such as the delay, the bandwidth, hops number, losses, etc. These objectives compete and conflict with each other. Such competition among conflicting objectives gives rise to a set of optimal solutions instead of a single solution [2].

This paper is organized as follows. Related work is presented in section II. Section III introduces a concise introduction to the GA. Multi-Objective optimization and Pareto Solutions are reviewed in section IV. In section V, a detailed description of the proposed AGA for routing in WMN is presented and discussed. The effectiveness of our proposed algorithm and the discussion of the simulation results are given in section VI. Finally, the conclusions are mentioned in section VII.

• II.    Related Works

Many works have been focused on routing in WMN. In [3], authors Proposed a multi-objective traffic engineering procedure utilizing various distribution trees to several multicasting flows. The purpose is to combine into a single united measure the bandwidth, hop count, supreme link utilization, and total delay. The work in [4] studied the performance of several algorithms for multiobjective Pareto optimization. These algorithms were tested on a set of standard benchmark problems. Where in [5] researchers proposed a novel technique for resembling the Pareto front of a Multi-Objective Optimization (MOOP) problem, where explicit forms of the objective functions are not available. The method iteratively approximates each objective function using a metamodeling scheme and employs a weighted sum method to convert the MOOP into a set of single objective optimization problems. A new alternate for the routing problem in WMN has been presented, which considers the QoS measure [6]. The actual case study includes several design objectives which conflict with each other. The new approach is tried to improve the routing solutions and proposes the use of Multi-Objective Evolutionary Algorithms (MOEA), specifically the Nondominated Sorting GA (NSGA). A mathematical model is introduced for this problem, which includes QoS parameters such as bandwidth, packet loss rates, and delay and power consumption. Jitter mechanisms can dramatically improve reactive routing protocols, in [7], jitter mechanisms are proposed which enforce wireless nodes to postpone their transmission for a random amount of time so as to reduce probability of simultaneous transmission. The work in [8] proposed a centralized MultiPAth QoS-driven Routing (MPAR) protocol for industrial WMN which included the end-to-end reliability requirements of the available paths. On the other hand, stability of wireless mesh networks is an important issue; instability in these networks is caused mainly by link quality fluctuations and frequent route flapping.

Authors in [9] addressed the stability problem of wireless mesh networks. A routing protocol which applied Software Defined Networks (SDN ) to multi-hop wireless network has been studied in [10]. The proposed protocol is implemented using OPNET simulation. For Hybrid WMNs, [11] proposed a load-aware cooperative hybrid routing protocol (LA-CHRP). This protocol is not only adapted to cover the peculiarities of routers and clients, but also considers load in routing. GA-based Multi-Path QoS Routing (MPQR) scheme is proposed for Polar-orbit Low earth orbit satellite networks [12].

The work presented in this paper is an extension for our previous works in [21]–[24]. In this paper, a new approach called Adaptive Genetic Algorithm (AGA) has been proposed by implementing the reproduction process with variable selection methods. The algorithm called adaptive because it chooses the selection method adaptively according to the best value of the fitness function that each of the six selections methods produces. Then the proposed Adaptive GA has been applied to obtain the shortest route in wireless networks where the nodes of the wireless networks are mobile with time.

• III.    A Genetic Algorithms (GA)

GAs are an evolutionary optimization approach, they are especially appropriate for applications which are vast, nonlinear and potentially discrete in nature. In GA, a population of strings called chromosomes (or individuals) which represent the candidate solutions to an optimization problem is evolved to the better population. It is more common to state the objective of GA as the minimization of some cost function rather than the maximization of some utility or fitness function[25],

^F(,)  1+/(t)

where f ( t ) is the cost function to be maximized. While the fitness is set to F ( t ) = f ( t ) when the problem needs f ( t ) to be minimized. GA consists of main three steps, these are: selection process, crossover, and mutation. The Selection process refers to the mechanism of choosing a set of chromosomes from the population that will contribute to the creation of the offsprings for the next generation [26]. Many methods have been proposed for mate selection in the literature, some of the important methods are described in our previous works [24], [27], these include Roulette Wheel Selection (RWS), Tournament selection (TS), Rank selection (RS), Steady-state selection (SSS),

Sigma scaling selection (SigSS) and Boltzmann selection (BS) . On the other hand, crossover operation, or mating, is the creation of one or more offspring from the parents selected in the pairing process. The final step of the GA is the mutation operator, it is another way of the GA to investigate the cost-surface and it can introduce individualities that never exists in the principal population and preserve the GA from converging too fast before searching the complete cost-surface [28], [29].

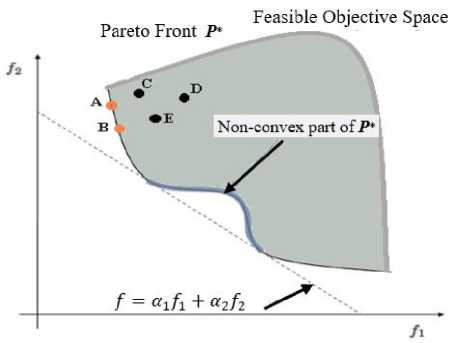
Fig.1. WS is unable to generate the Non-convex Part of the Pareto Front

• IV.    Pareto Approach for Multi-objective Optimization

For sound-organized mathematical problems, the weighted sum (WS) strategy achieves well and has decent scientific properties, for example, convergence. Nonetheless, the WS technique cannot create any point in the non-convex region of the Pareto front as illustrated in Fig.1. Point C, D, and E are not on the Pareto frontier because it is dominated by both point A and point B. Points A and B are not strictly dominated by any other, and hence do lie on the frontier. Additionally, WS technique may copy solutions with various weighting factors [5].

The second general approach for multi-objective optimization is to find whole Pareto optimal solutions or a typical subset. A Pareto optimal solution is a set of solutions that are non-dominated with each other. While traveling from one Pareto solution onto the next, there must be a sacrifice in one of the objective(s) to accomplish a specific improvement in the other(s) [30]–[32]. Genetic algorithms (GAs) work with a population of points, a number of Pareto-optimal solutions may be captured using GAs. A new algorithm called Nondominated Sorting Genetic Algorithm (NSGA) is presented in this work. This algorithm eliminates the bias in Vector Evaluated Genetic Algorithm (VEGA) [31], [32] and thereby distributes the population over the entire Pareto-optimal regions [33], [34]. In this work three objectives: an end-to-end delay, bandwidth, and a number of hops will be utilized as multiobjective measures using NSGA algorithm to test their convergence through the generations of the GA.

Definition 1 [35]: A solution x ⁽¹⁾ is said to dominate the other solution x ⁽²⁾ if both conditions 1 and 2 are true:

• 1.    The solution x ⁽¹⁾ is no worse than x ⁽²⁾ in all objectives: that is,

  /■(x⁽¹⁾) О / j (x⁽²⁾) for all j = 1, 2, 3, ...., M

• 2.    The solution x (1) is strictly less than x (2) in at least one objective, or

/j(x(1)) о/-(x(2)) for at least one J £{1,2,, M}

Operator < between two solutions i and j as < to denote that solution i is better than solution j on a particular objective. Similarly, i ▻ j for a particular objective implies that solution i is worse than solution j on this objective. If either of the above conditions is violated, the solution x (1) does not dominate the solution x (2). If x (1) dominates the solution x 12 (or mathematically x(1)  < x(2)), it is also customary to write any of the following:

• •    x ⁽²⁾ is dominated by x ⁽²⁾,

• •    x ⁽¹⁾ is non-dominated by x ⁽²⁾ , or x ⁽¹⁾ is noninferior to x ⁽²⁾

The set of all feasible solutions that are non-dominated by any other solution is called the Pareto- optimal or nondominated set. If the non-dominated set is within the entire feasible search space, it is called globally Pareto-optimal set. In other words, for a given MOOP, the Pareto-optimal set P * , is defined as:

P• = {x £ ПЬЭ x' e П ^/(x') < /(x)}

The values of objective functions related to each solution of a Pareto-optimal set in objective space are called Pareto-front. In another word for a given MOOP, f(x), and Pareto-optimal set, PF *, the Pareto front( PF *) is given by:

PF • = { u = f(x )| x e P * }

• V . The Proposed AGA For Routing In WMN

A Dynamic network under consideration represented as a connected graph with N nodes. The metric of optimization is the multi objective QoS (delay, bandwidth, no.of hops) of a path. The goal is to find the path with minimum total delay, maximum bandwidth, and minimum no. of hops as QoS between source node s and destination node d. The details of the algorithm are given in the following; while the investigation of the performance is achieved via a simulation work in the next section. Our contribution in this work lies in two points: the first is that the proposed algorithm deals with dynamic topology network where nodes are mobile, and the second contribution is the adaptive selection method used in the proposed AGA with proposed selection methods deals with 6 selection criteria, each generation is obtained using one selection method with best fitness. The proposed AGA consists of the following steps:

• A.    Priority-Based Encoding

When utilizing GA based routing in wireless networks, each candidate solution called a chromosome. The chromosome consists of sequences of positive integers that represent the IDentification (ID) of nodes through which a routing path passes. Each locus of the chromosome represents an order of a node in a routing path. A certain gene in a specific chromosome is described by the variables: allele , the value for that gene, and loci, the gene’s position. The gene’s position is utilized to characterize a node, while the priority for that node for developing a path from competitors is represented by the value of the gene. This strategy is signified as Priority Based Encoding as illustrated below (see Fig. 2).

Fig.2. Representation of Priority based Encoding

• B.    Representation

In this case-study, the wireless routing scheme is represented as the GA chromosome. A route list interprets the routing chromosome, such as P = (P 1 , P 2 …, P k ), which characterizes the complete network. Every route is a particular path between the source and destination nodes i and j. A route is coded by concatenating the nodes from the start node to the target node depending on the network topology. For example, a route starting from node number one to node number fifty can be denoted as a node vector along the route: {1, 2, 4, 12, 34, 50}, see Fig. 3. If a route cannot be achieved on the network, it cannot be coded into the chromosome.

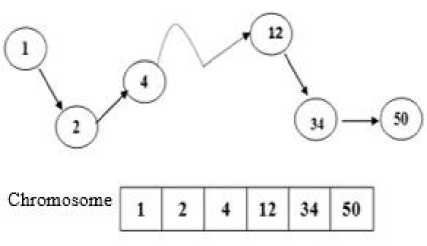
Fig.3. Example of Routing Path and its Encoding Scheme

• C.    Initial Populations

This underlying procedure is utilized to create the routing table in the present generation. Every chromosome incorporates an arbitrary routing table for the particular topology of the mobile network under study.

• D.    Multi-Objective Optimization

Different QoS criteria characterize routing in mobile wireless meshed networks, some of these criteria are a number of hops, an end-to-end delay, and bandwidth which are adopted in this work. Clearly, it can be fit into multi-objective optimization. In this work, we propose the design of a Multi-Objective GA (MOGA) through the Weighted Sum (WS) approach. This method is used in MOGA to attain the above three objectives through a single-objective measure by utilizing the convex combination of the design measures. Minimizing the fitness function means minimization of the weighted sum function F given by the following formula:

F = «1F1 + a2F2 + a3F3(2)

Where F 1 , F₂, and F₃ are the delay, the bandwidth, and the number of hops, given by,

F1 = min Delay(P(s , d))(3)

F2 = max Bandwidth(P(s , d))(4)

^'^ ~

F3= min Hop(P(s , d))(6)

Subject to

Delay(P(s , d)) <= Dmax Bandwidth(P(s , d)) >= Emin Hops(P(s , d)) <= Hopsmax where P(s , d) = P1,........Pn, is the collection of all the potential routes from source node s to destination node d, where a certain source-node s E V and destination-node dEV , V is the network nodes set (vertices), Delay(P(s, d)) = £Delay(V) is the total delay along the entire path P1,........Pn , Bandwidth(P(s, d)) = maxBandwidth(V) is the maximum bandwidth along the entire path  P1,........Pn , Hops(P(s, d)) =

£Hops(V) is the total number of hops along the entire path P1,........Pn, Dmax represents the maximum limit on end-to-end delay along each path, Emin represents the lower bound on the acceptable bandwidth along each path from a source s to the destination d, Hopsmax represents the upper bound on the acceptable number of hops along every route from the start s to the terminating node d. the weights «1 , «2 , a3 are understood as the relative importance of one objective function relative to the others. The values of «1, «2, «3 are selected to increase the selection weight on any of the three objectives, such that,

Z i ⁿ =i « i = 1                     (7)

• E.    Proposed Selection Process

Selection is an operator to select two (i.e., routing tables) for generating new chromosomes. To be selected as a parent chromosome, the chromosomes are competing each other during selection process based on the fitness value. Each chromosome has its fitness value calculated according to (2), more explanations on different selection operators used in this work can be found in our previous works [24], [27]. A chromosome with a high fitness value (i.e. minimum cost) subject to the delay, maximum bandwidth, and minimum number of hops has more chance to be selected as one of the parents using one of the six selection methods that had the minimum fitness value.

• F.    Path Crossover

To carry out the crossover operator, the chromosomes must have the same start and target nodes. The points in the chromosomes are constrained to the nodes that are common in both chromosomes. The most common and the simplest form of crossover is single point crossover. A crossover site is randomly selected on both chromosomes and exchanging the sub-routes when carrying out this operator to both chromosomes as depicted in Fig. 4.

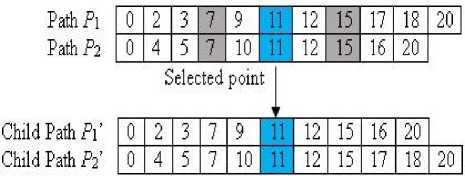
Fig.4. An Example of Single Point Crossover

Selecting node number 11 as a cross-node results in the child pair of chromosomes given as P 1 ’ and P 2 ’. The Procedure of the path crossover can be summarized in the following:

• 1.    Create list of nodes NC which exist in both P ₁ and P ₂ (excluding source s and destination d nodes) as possible a cross-point.

• 2.    From the list NC , pick a certain node i as a crosspoint.

• 3.    Exchange all the nodes for the parent chromosomes beyond the cross-point i to achieve the crossover process.

• G.    Path Mutation

The operator of the route mutation means generating another chromosome from the chromosome. To apply the mutation operator, firstly a single node is arbitrarily chosen from each chromosome, it is denoted the mutation’s site. At that point, another node is arbitrarily chosen from the set of nodes that are directly connected to the mutation site. In accordance with the shortest path problem, a second path is determined through linking starting node to chosen mutation node and from the chosen node to target node. As illustrated in Fig. 5, where the offspring P' signifies the route obtained by the mutation operator. The path mutation operator procedure is described as follows:

• 1.    From all nodes in parent P , randomly pick a node i as a mutation node.

• 2.    From the neighbors ( B ) of the mutation node i , select a node j ∈ B .

• 3.    Create two paths r 1 and r 2 with shortest distance, the first (r1) from the mutation node j to the source node ( s ) and the second( r 2) from the destination node ( d ) to node j .

• 4.    If nodes replication occurs between shortest paths ( r 1 and r 2), cancel the paths and stop mutation, else join the path to create a mutation node.

Parent P | 0 | 1 | 3 | 5 | 6 | 11 | 13 | 50 |

Sub-route n   | 0 | 2 |~4 J^

Sub-route n | 9 | 11 | 13 | 50 |

___

Offspring P' | 0 | 2 | 4 | 9 |'ll | 13 | 50 |

• Fig.5. An example of Mutation

• VI.    Main Results

In this section the simulation results of applying Adaptive Genetic Algorithm (AGA) on path routing in mobile wireless networks for triple objectives are presented. AGA has two features. First it is adaptive with the dynamic topology of the wireless network nodes, second the proposed AGA uses a new technique in the selection operator, selection of proper parents to produced new individuals, it uses six selection methods working simultaneously, and the fitness value for each selection method is calculated; depending upon the best value of the fitness, we choose the selection method which gives best parents to produce new offsprings. The proposed algorithm applied on multi objectives of QoS measures, measuring all of the three objectives together, i.e. end-to-end delay, bandwidth, and the number of hops, the results are presented using weighted-sum approach with the aid of Pareto analysis.

A network model is obtained by G ( V , E ), where G is a graph and V is the collection of the nodes of the network, and E is the collection of the connected linked edges. The simulation network parameters are chosen as follows: Number of nodes = 50, as shown in Fig. 6. Topology-area: Nodes are distributed randomly on 1000*1000 m ², the area of the node coverage equals to 200 m , node 1 is the source node (s), while the destination node (d) is node 50. Population size equals to 50, selection method used in this project are {RS, SSS, BS, RWS, SigSS, TS}, number of generations equals to 100, the crossover probability equals is Pc = 0.75, mutation probability is Pm = 0.01.

We have fifty routes from s to d, and each route has a fitness number depends on its delay, bandwidth, and number of hops from s to d. We have to find one optimum path among the fifty paths (50 paths) available with minimum delay, maximum bandwidth, and minimum no. of hops. The values of a1, a2, a3 are 0.5, 0.15, 0.35 respectively. The values of the fitness functions with each selection technique are represented by their minimum and maximum values, as illustrated in Table 1. They are applied at the same time. Our experiment concerns about the maximum value of the path bandwidths, minimum values of end-to-end path delays, and minimum path hops.

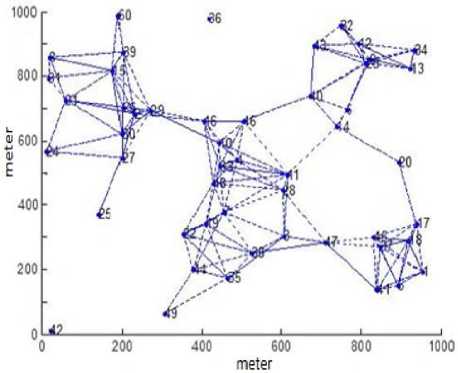
Fig.6. The Network Model of 50 Nodes

Table 1. Selection Method of Multi-Objectives QoS

Selection method Index	Selection method	Maximum	Minimum
1	RWS	15.28	11.92
2	TS	15.46	11.62
3	SSS	15.36	11.92
4	BS	15.42	11.92
5	Sig SS	15.42	11.92
6	RS	16.15	11.92

The outcomes of implementing our proposed AGA are illustrated as next, the shortest path from the starting node s to the destination node d was {1 24 26 46 50} as depicted in Fig. 7. The end-to-end delay was {8 msec}, bandwidth was 1.9932 Mbps and a number of hops was 4. The best fitness value was (10.2968) resulted from selection method 3, namely, the SSS selection method. Therefore, the SSS selection method gives the best fitness. Fig. 8 showed the variation of the fitness values during iterations of the AGA. Additional results for the multiobjective QoS experiment were presented in Figs. 9 and 10, where Fig. 9 shows the values of the QoS parameters of some paths, P1, P2, P3, P4. It can be concluded that P4 is the best optimum path among them. Fig. 10 showed the fitness values for the multi-objective QoS for various paths, P1, P2, P3, P4 knowing that path four P4 is the optimum path. To solve multi-objective optimization using AGA with Pareto solution approach, two main goals must be attained. The first goal is to converge to a set of the solution as close as possible to true Pareto- optimal set, and the second goal is the diversity in the obtained Pareto-optimal set. With a more diverse set of solutions that covers all parts of the Pareto-front in objective space, the decision making the process at the next level using the higher level information is easier. The diversity in the two-dimensional space is often symmetric, however in three -dimensional space (three objectives problem) and the non-linear problem the diversity is more difficult to obtain. Fig.11 (a) illustrated the Pareto optimal solutions of the three objectives optimization, where f(x1), f(x2), f(x3) represent an end-to-end delay, bandwidth, and a number of hops respectively. The population size was 50 and the number of generations were 100, 200, 4000, and 10000. The diversity and the convergence of the Pareto solutions were very obvious. The weighted-sum approach represented the Pareto solution to the multi-objective optimization; this was clear from Fig. 12.

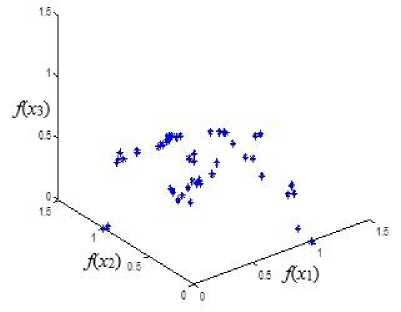
There are fifty potential paths from the starting node s to the destination node d as an initial population. Six different selection methods are used in every generation in the suggested AGA. The extreme values of the fitness function are computed using these measures and are listed in Table 1. The best selection method is chosen for which the fitness function is the lowest because our work is of minimization type. The algorithm is ended when a maximum number of generations reached which is considered to be 100. From the above simulations, it can be seen that with the optimum path P₄, the bandwidth is less than in the remaining paths, this is true because of the weighting factors that the WS approach adopts, where the weight a₂ = 0.15 has been used for optimizing the bandwidth. On the other hand, the end-to-end delay and the minimum number of hops in the optimum path P4 were less than from the other paths, this is due to the high values of the weighting factors that have been used to optimize these objectives ( « 1 = 0.5 for the delay, a₃ = 0.35 for the number of hops). To discuss how the WS approach can represent the Pareto Solutions, we proceed as follows, the general formula of the WS approach to MOGA is represented by (2). The values of a 1 , a₂, a₃ are chosen to increase the selection pressure on any of the two objective functions. In order to represent the Pareto technique, the weights a 1 , a₂, a₃ play a key role in this process. Which can take random values. So the WS approach can almost represents all solutions as shown in Figure 12. In this Figure, the poin, ts in red color represent the solution produced by letting a 1 , a₂, a₃ take values of 0.5, 0.15,0.35 respectively, which are used in our design. The other points of blue color represent random values of a 1 , a₂, a₃. The total (red and blue) points represent the Pareto solutions. We conclude that the weighed-sum solution is a part of the whole possible Pareto solutions. Finally, When the results obtained from this work compared with another traditional technique, like dynamic programming techniques, we found that our proposed AGA performs better, where the total no. of hops and end-to-end delay obtained from our proposed AGA are 8 msec and 5 respectively as compared to 21 msec and 7 in [22]–[24], [27].

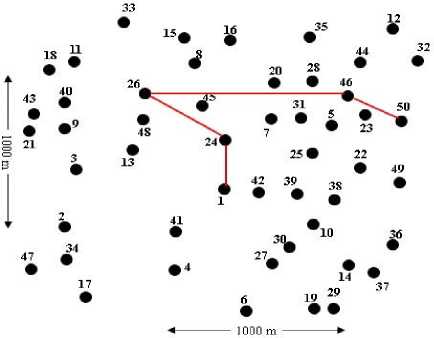
Fig.7. Network Topology is showing the Optimal Path (red line) Satisfying Multi-objectives QoS Measures, Delay, Bandwidth, and a Number of Hops.

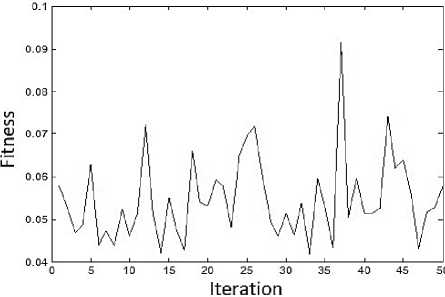
Fig.8. Normalized Fitness Variation through Iterations for Multiobjective QoS.

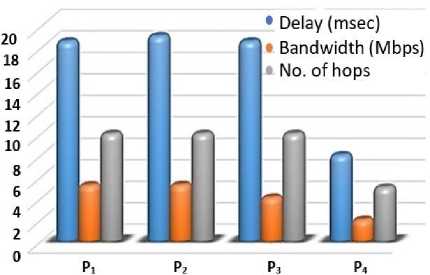
Fig.9. Multi-objective QoS Parameters for the four Paths.

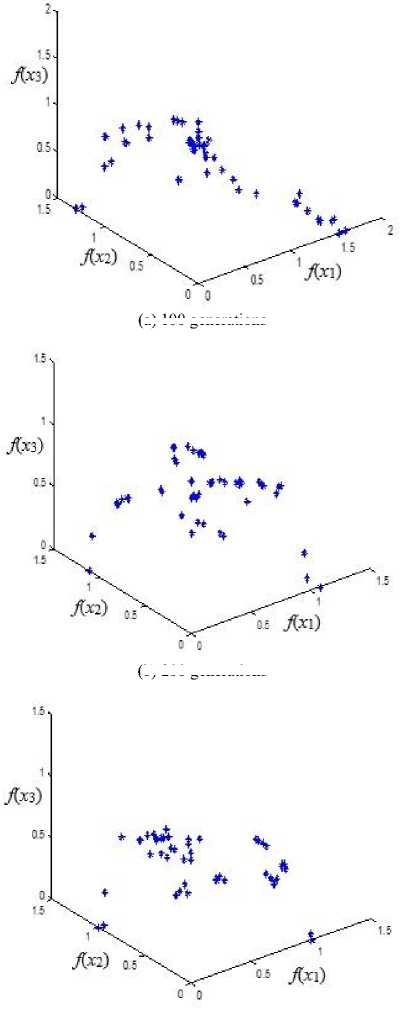
(a) 100 generations

(c) 4000 generations

(b) 200 generations

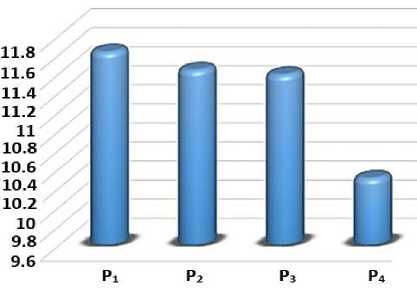
Fig.10. Fitness Value of Multi-objective Parameters for four Paths.

(d) 10000 generations

Fig.11. Pareto Solutions with Different Generations.

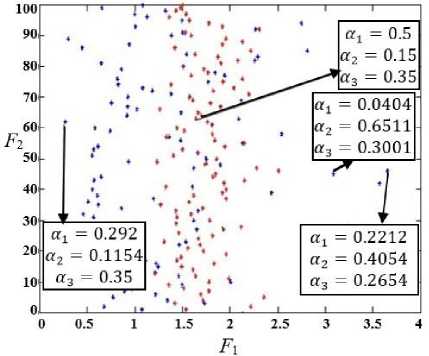
Fig.12. Weighed-sum Solution and Pareto Solutions Correlation. The Points in red are the Solution with « 1 , « 2 , « 3 take values of 0.5, 0.15,0.35. while blue Points are the Solutions with Random Values of « 1 , « 2 , « 3 .

• VII.    Conclusions

Multi-objective QoS measures are achieved in this paper, these are end-to-end delay, Bandwidth, and a number of hops. Each one of them reflects the importance of a particular property in the wireless networks. To get better efficiency in the performance of WMN, we applied MOOP to these objectives together. The suggested AGA is able of finding the solution for the multi-objectives wireless routing problems and gets the optimal solutions faster than the conventional procedures. The selection methods utilized in the suggested AGA of this work considerably had a direct effect on the behavior of the algorithm, it broadened the searching field and improved the procedure of the selection process. In the suggested algorithm, the proposed AGA adjusts quickly with changing networks environment, e.g., wireless networks with mobile nodes. On the other hand, concerning Pareto solutions, the diversity can be achieved as the number of generations increases, which makes the decision process easier at the higher level. Generally, they are not symmetric for higher dimensional spaces.

Acknowledgment

The Authors thanks Electrical Engineering Department at the University of Baghdad for financial help and support.