A new approach for data hiding based on pixel pairs and chaotic map

Rapidly developing and changing technology has led internet-connected electronic devices to be cheaper and commonly used [1]. While this situation facilitating access to information, it has become an important issue of ensuring information security. Information security is become important topic in digital world [2]. The main purpose of information security is to prevent the third-parties from capturing the digital data during storing and transmitting processes [3,4]. There are various methods in information security applications such as data hiding, cryptography etc. In this applications, data can be encrypted or its existence can be hidden by using a cover object. Cover object can be multimedia such as text, audio, video and image [5-7]. Multimedia data is frequently used in data hiding applications because of high payload capacity [8]. If small changes in cover object can’t detected by human perception system, the application is considered as successful. Criteria such as bit error rate (BER) [9], peak signal-to-noise ratio (PSNR) [10, 11], structural similarity (SSIM) [12] are used to utilized success of data hiding application. A lot of data hiding methods are evaluated with this criteria [13-17]. There are two kind of data hiding application. The first data hiding application is spatial domain. Spatial domain applications changes pixel values, frequency domain applications use frequency coefficient for data hiding applications. Discrete Wavelet Transform, Discrete Fourier Transform and Discrete Cosine Transform are used to obtain frequency coefficients and these coefficients are modified for data hiding in frequency domain. If robustness against corruptive situation is important, frequency domain applications are preferred. For this reason, performing data hiding according to purpose of application increases performance of data hiding algorithm.

The paper is organized in 6 sections. The literature review about related works is given in section 2. In section 3, chaotic maps are introduced. the proposed method is described in section 4. In section 5, the obtained results are illustrated. Finally, conclusion of this paper is presented in section 6.

• II.    Related Works

There are a lot of studies about data hiding in literature. Chen [18] presented a Pixel Value Difference ( PVD ) method to safely hide data that is secure. The results demonstrated high capacity and cover object quality in comparison to other similar method. Shen and Huang [19] proposed a data hiding algorithm to increase embedding capacity based on pixel pairs. Their method demonstrated both to improve needed embedding capacity and to hold stego image quality. Qu and Kim [20] introduced a novel pixel-based pixel-value-ordering ( PVO ). Their obtained results indicated the good performance of the proposed pixel-based PVO method based on each predicted pixel. Wang et al [21] provided a new data hiding approach using PVO and dynamic pixel block partition. Their proposed scheme demonstrated a better capacity than current PVO based method. The method also tries to minimize distortion to the minimum. Lin and Hsueh [22] presented a reversible data hiding method used pixel pairs. This method embedded to ensure lossless a data into a cover object using pixel pairs in a three-pixel block. The average capacity of their proposed method for images measured with bpp (2.08 bit per pixel). Li et al [23]

proposed a high accuracy reversible data hiding approach in test images based on PVO and prediction-error expansion ( PEE ) method measured by PSNR value which found about 51.14 dB. Tsai et al [24] come up with a new data hiding scheme in test images using the histogram method. This algorithm was obtained high embedding capacity and imperceptible distortion. Hong et al [25] presented a data hiding approach based on the diamond encoding ( DE ) technique. This method with the consideration of human visual system provides better quality and high embedding capacity. Yang et al [26] presented a new data hiding approach using pixel-value differencing ( PVD ) for increase the embedding capacity. Their experimental results were compared with other similar method. This method obtained better embedding capacity. Lee et al [27] proposed data hiding algorithm to increased capacity with quality recovery based on tri-way PVD . Their experimental results demonstrated a high resistance to dual statistics steganalysis. Peng et al [28] presented a data hiding approach based on PVO and PEE . This method obtained better embedding performance compared to similar methods. Chang et al [29] provided a hiding algorithm using a multilevel histogrammodification method using the difference of neighboring pixels. This method had better capacity and cover object quality.

• III.    Chaotic Maps

Random numbers are required for perform various purposes in computer systems such as encryptions algorithms, game programing etc. For example, random numbers are very important for security and performance of encryptions algorithms. Random number generators ( RNG ) are used for generate this numbers. However, if seed values of RNG are estimated, this random numbers can be obtained. If generated numbers of RNG are same in each iteration, this is an undesirable situation especially for security applications. The main purpose of RNG is to generate a different seed value in each iteration. To avoid this undesirable situations new methods are developed for RNG . Chaotic maps are used as RNG for solving these problems. A chaotic system can be defined as system that sensitive to initial conditions and unpredictably complex. Small changes in initial conditions of chaotic systems cause big changes in this system. In this situation, chaotic systems become unpredictable.

A chaotic system describes in below.

• -    It is not random. It has an arrangement in itself.

• -    It is sensitively depended of initial conditions.

0.5     1     1.5     2     2.5     3     3.5      4

In parallel to this purposes, there are a lot of chaotic maps such as logistic map, gauss map and tent map. The widely used chaotic map is logistic maps. Logistic map developed by Robert MAY in 1976 was constructed on changes based on feedback of biological population [10, 30]. Logistic map is defined in Equation (1).

x„+i = pXn(1 - Xn),0 < р < 4,xu е (0,1)   (1)

According to р parameter system behaves chaotic or not chaotic [31, 32]. x is the initial seed and p is control parameter. Bifurcation diagram of logistic map is given in Fig. 1 [33].

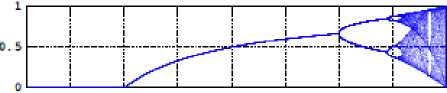
Fig.1. The Bifurcation Diagram of Logistic Map

• IV.    The Proposed Method

The purpose of proposed method is to increase visual quality and obtain a data hiding algorithm which has a short running time. This data hiding algorithm has high payload capacity. Modulo 4^b operator is used for determine payload capacity. b expresses payload capacity. For example, if 1 bpp payload capacity is used, process is performed according to modulo 4 , if 2 bpp payload capacity is used, process is performed according to modulo 16 . One of the biggest advantages of this method according to xLSBs (x Least Significant Bits Insertion Method) is less distortion rate on cover image by using high data hiding capacity. Privacy of secret data is also ensured by using chaotic maps and the proposed method has better running time than xLSBs because xLSBs algorithms are commonly used decimal to binary transformation on each pixel value for data hiding. This situation creates +1 iteration in algorithm. However, the proposed method doesn’t need decimal to binary transformation on each pixel value.

Data hiding steps of proposed method in this paper is given in below.

Step 1: Generate chaotic map by using seed values. The chaotic map must be same size with secret data.

Xi+1 = pXi(1-Xi),p = [3.57,4], xi е (0,1), Xi ^ 0.5, i = {1,2,3, ..., n}

"xt < 0.5, xt = 0

,Xi > 0.5, Xi = 1

^x i {

Step 2: Encode secret data by using modulo function. For example, if 1 bpp payload capacity is used, secret data is encoded with 2 bits, if 2 bpp payload capacity is used, secret data is encoded with 4 bits.

Step 3: Select operator according to value in chaotic map. If value is 0 , select subtraction operator, otherwise select summary operator for pixel pairs.

f 0,d = |C7i,2y-C7i,2y+i|(mod4b)

Xi,] ( 1, t = CIi,2j + CIi,2j+i (mod4b)

i = {0,1,2,... r-1},;={0,1,2,^f-1} d is difference of pixel pairs, CI is cover image and t is summary of pixel pairs.

Step 4: Equal obtained t and d values to secret data. For example, random values which are obtained from chaotic map is (1011)₂, secret data is (01111000) 2 and cover image pixel values are given in Fig. 2. Data hiding process is applied in below.

128	133	117	85
250	25	0	255

Fig.2. The Sample Image Pixels

If value of chaotic map is 0 , subtraction operator is selected, otherwise summary operator is selected for pixel pairs.

(0,d = ISIUj-SIii2j+1l (mod4b) X/4 1,t = SI/-2j+SI/,2j+1 (mod4b) i = {0,1,2,^ r-1},;={0,1,2,^f-1}

128+133 (mod 4) = (01) 2 , 128 and 133 pixel values don’t change because the first two bits of secret data is (01) 2 .

|117-85| (mod 4) = (00) 2 , and secret data is (11) 2 . The small one of pixel pairs is increased by 1 . The obtained final values are 117, 86.

250+25 (mod 4) = (11)_2, and it is sufficient to decrease one of the pixel pairs by 1 because secret data is (10) 2 . The obtained new values are 249, 25.

255+0 (mod 4) = (11) 2 and secret data is (00) 2 . Increasing one of the pixel pairs by 1 is required to equal summary value to (00) 2 . The big pixel value is 255 , for this reason this value is not increased. The small value is increased by 1 and the obtained new values are 1 , 255 .

Secret data is embedded as (01111000) 2 and the obtained pixel values are shown in Fig. 3.

128	133	117	86
249	25	1	255

Fig.3. The Pixel Values of Stego Image

Data extraction steps are given in below.

Step 1: Generate chaotic maps by using seed values.

Step 2: Apply Equation (4) to pixel pairs of stego image and obtain secret data.

d is difference of pixel pairs, b is payload capacity, SI is stego image and t is summary of pixel pairs. For example, chaotic map is generated by using seed values to obtain data which is embedded into pixel values and 1011 is obtained by receiver from chaotic maps.

SD1=128+133 mod 4 = (01) 2

SD2=|117-86| mod 4 = (11) 2

SD3=249+25 mod 4 = (10) 2

SD4= 1+255 mod 4 = (00) 2

(01111000) 2 is obtained from stego image after steps in above.

• V.    Experimental Result

  The proposed method is evaluated on a computer with Windows8.1 operating system. The obtained results are utilized using MATLAB 2014a. In this study, after secret data in different sizes are embedded into test images, test images [34] and Kodak image data set [35] are evaluated according to the widely used criteria in the literature These images given in Fig. 4 are 512x512 sized and grayscale. These test images are named as Lena, F16, Baboon, Barbara, Boat, Pepper, House, Sailboat, Elaine, Tiffany, Goldhill, Toys and Zelda. PSNR [36] and Quality (Q) [37] given Equation 5-12 are used to utilized the result of proposed method.

(a)

(b)

(c)

(f)

(h)

(j)

(l)

(m)

Fig. 4. The test images (a) Lena, (b) F16, (c) Baboon, (d) Barbara, (e) Boat, (f) Pepper, (g) House, (h) Sailboat, (i) Elaine, (j) Tiffany, (k) Goldhill, (l) Toys, (m) Zelda

W^^M

-Slij)

Max(Cl2j) PSNR = 10 log--—^ MSE
	(6)
4axy x x y	(7)
(^ X + f y )[ x2+y2 ]
^-Lm-A m x n   i 1  11   i,J	(8)
y = ^Y ^ ^ ^ Siu mx n   i 1   J 1    i,J	(9)

Table 1. The obtained In Terms of PSNR (dB) the Proposed Method with the Embedding Capacity of 10,000 and 20,000 bits

Image	10,000 bits	20,000 bits	Image	10,000 bits	20,000 bits
Lena	63.0	60.0	Barbara	63.2	60.2
Baboon	63.2	60.0	Tiffany	63.1	60.1
F16	63.4	60.2	Elaine	62.9	59.9
Boat	63.2	60.0	Sailboat	63.3	60.1
Pepper	63.3	60.0	House	63.4	60.5

O x =	1 m x n-	- ТЫ П = 1 (С1Ц -	x)2	(10)
O x =	1 m x n-	- Z i=1 Z n = 1 (ci iJ. -	x)2	(11)

Oxy = ^^Z™iZ"(C7i,; - xXSIij - y) (12)

Here,

CI i j    — Cover image

^SI ij   — Stego image

• m     — Weight of cover/stego image

• n      — Height of cover/stego image

The mean value of cover image, stego

• ^X, ^y       image, respectively

0 2 O y — The variance of cover image, stego image

The covariance of the values from the xy      stego image and cover image

Table 2. The obtained of Kodak Image Data Set in Terms of PSNR (dB) for the Proposed Method with the Embedding Capacity of 10,000 and 20,000 bits

Image	10,000 bits	20,000 bits	Image	10,000 bits	20,000 bits
kodim01	64.76	61.64	kodim13	64.77	61.61
kodim02	64.91	61.76	kodim14	64.86	61.75
kodim03	64.75	61.96	kodim15	64.66	61.78
kodim04	64.96	61.83	kodim16	64.80	62.00
kodim05	64.95	61.83	kodim17	64.89	61.92
kodim06	63.54	61.35	kodim18	64.85	61.73
kodim07	64.71	61.97	kodim19	64.79	61.86
kodim08	64.82	61.66	kodim20	63.55	61.37
kodim09	64.77	61.76	kodim21	64.86	61.88
kodim10	64.84	61.83	kodim22	65.17	61.97
kodim11	64.26	61.81	kodim23	65.07	62.17
kodim12	64.91	61.94	kodim24	63.78	61.19

The proposed method is compared for 10.000 bits and 20.000 bits sized secret data by using test images and Kodak images data set. The obtained results are shown in Table 1-2.

The proposed method is compared with Shen and Huang method [19] and obtained results is given in Table 3.

Table 3. Comparisons of Test Images In Terms of PSNR (dB) for Shen and Huang Method and the Proposed Method

Shen and Huang Method 2015
Image	PSNR	Capacity	Error
Lena	42.46	402.485	0
Baboon	38.88	443.472	0
Barbara	40.15	425.340	0
Elaine	42.98	398.250	0
Goldhill	41.80	405.956	0
Boat	41.60	408.777	0
Sailboat	41.29	411.306	0
Toys	42.52	402.011	0
House	41.16	412.354	0
Zelda	43.43	396.553	0
Average	41.63	410.650	0
The proposed method

Image	PSNR	Capacity	Error
Lena	44.2868	450.240	0
Baboon	44.2969	450.240	0
Barbara	44.3053	450.240	0
Elaine	44.3123	450.240	0
Goldhill	44.3073	450.240	0
Boat	44.3212	450.240	0
Sailboat	44.2960	450.240	0
Toys	44.2800	450.240	0
House	44.2999	450.240	0
Zelda	44.3195	450.240	0
Average	44.3000	450.240	0

The proposed method is also compared with other data hiding methods [38, 39, 19] based on pixel pairs in literature in terms of Quality metric and the obtained results are shown in Table 4.

Table 4. Comparisons of other Methods [38, 39, 19] and the Proposed Method for Quality

Cover Image	hang and Lu method (2006)		Lu et al. method (2014) (|B|=4)		Lu et al. method (2014) (|B|=8)		Shen and Huang method (2015)	The proposed method
	Q,(T=15)	Q,(T=42)	Q,(T=3)	Q,(T=18)	Q,(T=3)	Q,(T=18)	Q	Q
Baboon	0.9913	0.9297	0.9955	0.9807	0.9858	0.9768	0.9977	0.9996
Lena	0.9951	0.9914	0.9978	0.9943	0.9934	0.9910	0.9992	0.9997
F16	0.9948	0.9815	0.9971	0.9923	0.9914	0.9863	0.9990	0.9996
Pepper	0.9960	0.9892	0.9983	0.9963	0.9951	0.9938	0.9995	0.9995
Average	0,9943	0,97295	0,9971	0,9909	0,9914	0,9869	0,9988	0,9996

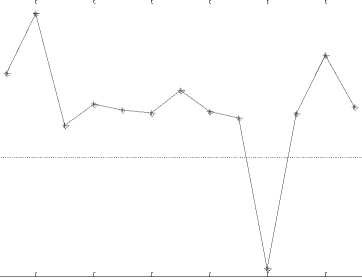
The PSNR change rates obtained from test images are given in Fig. 5 for 1 bpp payload capacity.

presented in Fig. 6 for 1 bpp payload capacity.

49.6

49.4

49.2

48.8

48.6

48.4

0           2           4           6           8           10          12          14

Test Images

Fig.5. PSNR Values of Test Images for 1bpp Payload Capacity

48.2

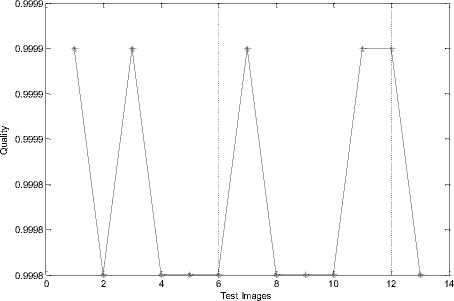
Fig.6. Q Values of Test Images for 1bpp Payload Capacity

The Quality change rates obtained from test images are

The PSNR change rates obtained from test images are given in Fig. 7 for 2 bpp payload capacity.

0.9965 0

0.9995

0.999

0.9985

0.998

0.9975

0.997

68 PSNR

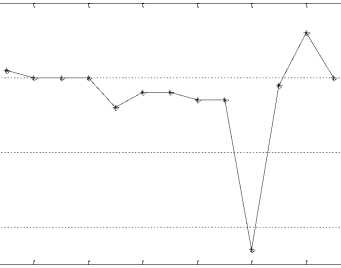
Fig. 8. Q Values of Test Images for 2bpp Payload Capacity

Test Images

Fig. 7. PSNR Values of Test Images for 2bpp Payload Capacity

The Quality change rates obtained from test images are shown in Fig. 8 for 2 bpp payload capacity.

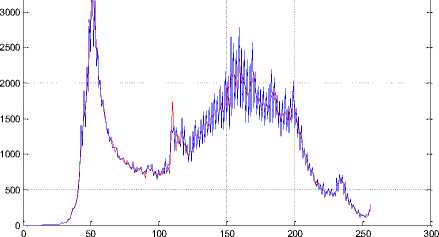
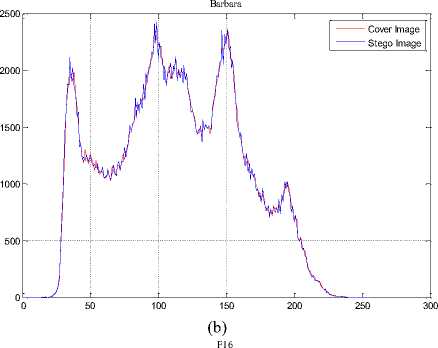
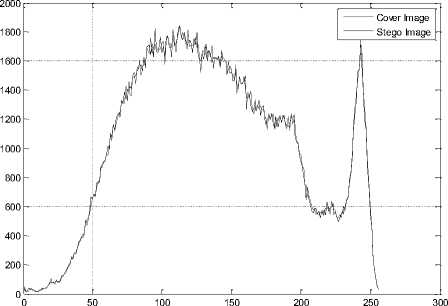
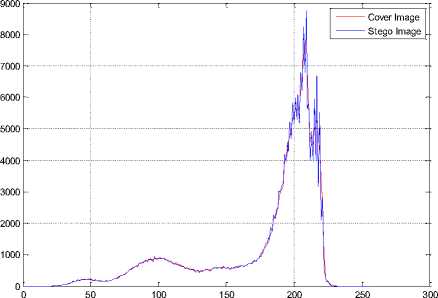
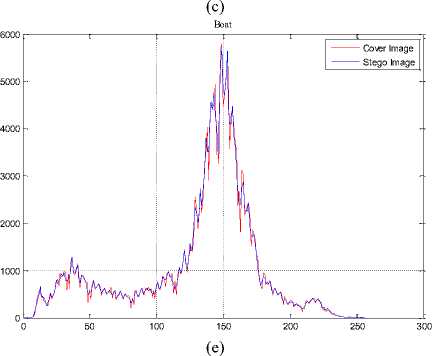
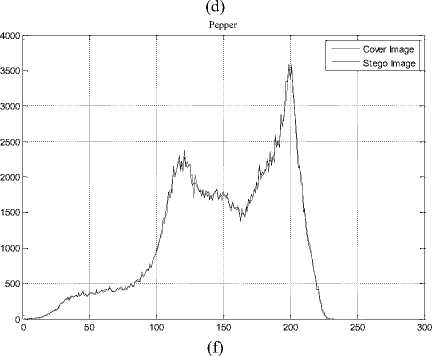
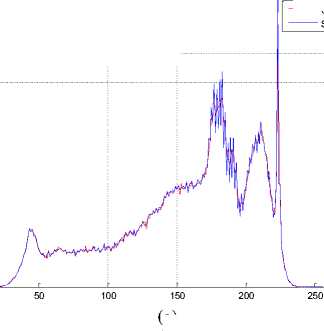
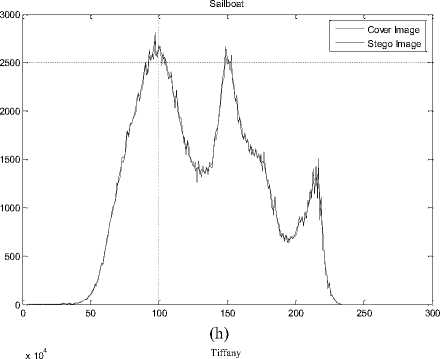
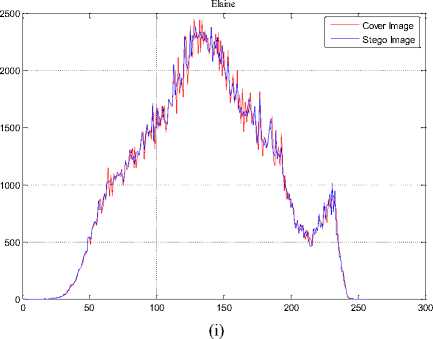
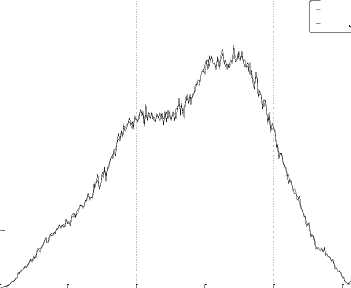
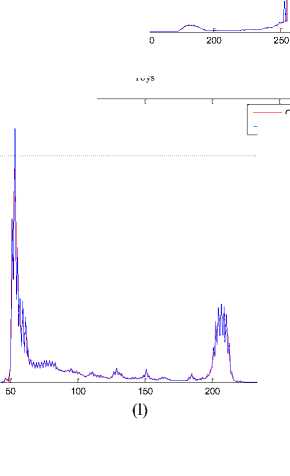
The histogram changes of selected test images are given in Fig. 9.

Lena

Cover Image

Stego Image

(a)

Baboon

House

Cover Image

(g)

Cover Image

Stego Image

Goldhill

Cover Image

Stego Image

(k)

x 104

2.5

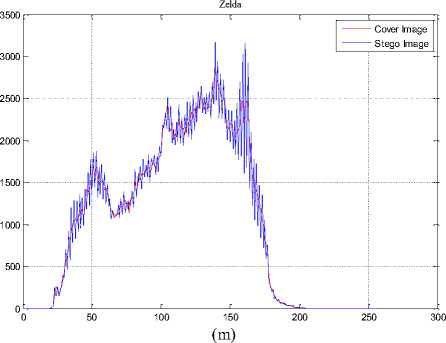
Fig.9. The Histograms of Stego Image and Cover Image for Test Images

(a) Lena, (b) F16, (c) Baboon, (d) Barbara, (e) Boat, (f) Pepper, (g) House, (h) Sailboat, (i) Elaine, (j) Tiffany, (k) Goldhill, (l) Toys, (m) Zelda

(j) Toys

Cover Image

Stego Image

Data embedding and data extracting processes running time of proposed method is also given in Table 5.

Table 5. Running Times of data Embedding and Data Extracting Processes for Test Images

Test Images (512x512)	Time (sec) for 1 bpp
	Data Embedding	Data Extract
Lena	0.069168	0.048932
Barbara	0.064320	0.045023
Baboon	0.067654	0.043105
F16	0.069114	0.049731
Boat	0.069092	0.056022
Pepper	0.076035	0.053498
House	0.062452	0.037706
Sailboat	0.072378	0.052184
Elaine	0.070545	0.052636
Tiffany	0.065044	0.043495
Goldhill	0.066420	0.044093
Toys	0.068566	0.050303
Zelda	0.065619	0.043780
Average	0.068185	0.047731
Test Images	Time (sec) for 2 bpp
(512x512)	Data Embedding	Data Extract
Lena	0.113872	0.047254
Barbara	0.108884	0.050283
Baboon	0.111490	0.051427
F16	0.109973	0.048256
Boat	0.108841	0.048606
Pepper	0.107190	0.048639
House	0.109721	0.049101
Sailboat	0.111420	0.049183
Elaine	0.109541	0.045971
Tiffany	0.110721	0.047532
Goldhill	0.111603	0.048779
Toys	0.106451	0.048197
Zelda	0.108448	0.047728
Average	0.109858	0.048535

• VI. Conclusions

In this study, a data hiding algorithm based on pixel pairs and chaotic map is proposed. The obtained results by applying summary-modulo or subtraction-modulo operation to pixel pairs are equaled to secret data. Chaotic maps which have statistically powerful features are used in proposed method for providing privacy of secret data. The operation between the pixel pairs is selected according to chaotic maps. Thus, the randomness of processes and privacy of secret data are provided. To avoid overflow/underflow situations, different rules are described for boundary pixel values. 1 bpp and 2 bpp payload capacity are embedded into test images. The obtained results are compared using PSNR, capacity, quality, running time with previous selected similar methods. In test images, the average PSNR values are 63.2 and 60.1 for 10.000 and 20.000 payload capacity, respectively. The average PSNR values are 64.67 and 61.77 for 10.000 and 20.000 payload capacity in Kodak image data set, respectively. At the same time, the average capacity is 450.240 in selected test images. In test images (512x512), the average running times are 0.068185 and 0.047731 for data embedding and data extracting, respectively. According to the obtained results, the proposed method is obtained to be better than the comparative similar methods. The proposed algorithm has high payload capacity, high visual quality, good security and good running time. In the future time, a better data hiding algorithm can be performed by normalizing coefficients in frequency domain.