A New Automatic Selection Method of Optimal Segmentation Scale for High Resolution Remote Sensing Image

Published Online March 2017 in MECS

Object-oriented feature extraction is the basis and precondition for high resolution remote sensing image analysis. Because the high resolution remote sensing image is rich in information, complex in type, and different types of objects correspond to different scales, a single segmentation scale cannot meet the application requirements. In object-oriented high resolution remote sensing image analysis, the multi-scale segmentation method is often used to provide the corresponding scale for different types of objects. In order to ensure the precision of image information extraction, it is necessary to understand the effect of image information on the scale of image segmentation. Therefore, the scale conversion of image information and the choice of optimal scale are the basic problems to be solved in object-oriented image analysis [1].

Traditional multi-scale segmentation has strong subjectivity. As a suitable segmentation result is obtained by visual judgment and repeated trial and error, it is difficult to establish an optimal scale segmentation model

• [2] . From the perspective of ensuring the homogeneity and division of image objects, Huang Huiping and Sun Bozhong proposed the criterion of image optimal segmentation. The internal heterogeneity of the object is as small as possible, at the same time, the heterogeneity between different types of objects is as far as possible big, and object can express the basic features [1,  3].

According to the segmentation criteria, there is no objective, quantitative and universal multi-scale image model to determine the optimal segmentation parameters at home and abroad [2].

Markov random field is an effective and commonly used tool in image segmentation. It can depict the image spatial dependency effectively. It can transmit the context information to the whole image through the local interaction of the information. Finally the image object network hierarchy of different scales can be constructed. Laferte and Wang Xili[4,5] and other fixed quadtree structure to establish multi-scale MRF model. This method can get better results through the causal relationship between levels of message passing. However, this method can cause the block effect of the segmentation results, and error segmentation is easy to transfer between levels [6]. Todorovic and other [7] used dynamic tree technology to solve the error classification of multi-scale MRF model, but the computation of dynamic tree model is larger. Poggi adopted supervised tree-structure MRF model to construct hierarchy. But the interaction process of the model is complex, and the level determination is subjective [8]. In order to improve the computing speed of MRF model, belief propagation algorithm was applied to model reasoning [9]. However, the segmentation result is not ideal. Yang et al applied multi-grid BP algorithm and used the rapid convergence strategy to effectively reduce the computational redundancy of the BP algorithm. Although the algorithm improves the operation speed, it can easily lead to false segmentation [6]. LIU Guanghui et al put forward the BP algorithm based on multi-scale MRF model. As it can effectively reduce the problem of slow message passing in long distance pixels by the large scale of the message, the operation speed is improved. At the same time, the method can obtain better results [10]. The existing image MRF model often adopts the top-down approach to construct the hierarchical structure of the image. Since the establishment of the finest scale image depends on the calculation of all the pixels in the image, it brings the problem of long operation time. Because the pixel information is single, it is easy to cause the error classification of pixels.

In this paper, a multiscale BP algorithm based on MRF model is proposed, which is based on the bottom-up approach, and the hierarchical structure is established to extract the optimal segmentation scale of high resolution remote sensing image. Firstly, the algorithm introduces the watershed algorithm to divide image into a number of homogeneous and uniform regions. The segmentation result is the finest scale image. The local regions are regarded as the object nodes. The spectral, color and texture features of the local area are introduced into the object nodes. Then, feature information is transferred between object nodes in the same level and between different levels. The consistency probability of object node feature information is estimated by MAP. Finally, the neighborhood object nodes with similarity maximum are merged. Thus, the global optimal segmentation scale selection can be realized automatically. The experimental results show that compared with the standard BP algorithm based on MRF model, the proposed method can improve segmentation quality and computation speed efficiently.

The rest of the paper is organized as following. Section 2 briefly reviews multi-scale segmentation MRF model. In Section 3, automatic extraction algorithm on the optimal segmentation scale is described in detail. Experimental results and analysis is displayed in section4 . Finally, Section 5 draws a conclusion.

• II.    Multi-Scale Segmentation MRF Model

• A.    MRF Image Model

Markov random field model is a conditional probability model for describing image structure. MRF model describes the interaction relationship between elements in space, and considers that the properties of the image elements are only related to the location of the neighborhood, but not to the elements of the other locations.

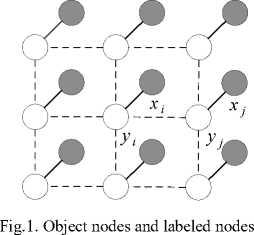
Let X ={*v x₂, ⋯ } denote the observed image where the nodes are not identified, where X[ is the i -th node of the image and N is the total number of nodes of the image. Y ={У1’ У2’ ⋯ } is an implementation of X and represents the label random field after image segmentation, where yi is the label corresponding to the

• i -    th node of the observed image and Yi ∈ {1,2, ⋯ , L } . L represents the total number of observations in the image classification.

As shown in Fig.1, each labeled node Yi corresponds to an observing node X[ in MRF model. MRF model describes the spatial structure features and dependencies of adjacent elements in images. Under the framework of Bayesian statistical learning, it makes full use of the various features of the image and priori knowledges, and solves the problem by using the maximum a posteriori (MAP) criterion. In image analysis, the MRF model expresses the local structure information by the form of conditional probability. However, it is usually difficult to infer the local conditional probability to the global joint probability. Hammersley-Clifford theorem proves the equivalence between MRF and Gibbs distribution [11], so that the Gibbs distribution can be used to facilitate the calculation of MRF joint probability.

According to Hammersley-Clifford criterion, the global Gibbs energy distribution is determined by computing the cluster potential function. Therefore, the joint probability distribution of MRF is as Eq.(1).

p ( X , Y )= ∏ [Ф[ ( Xi , Yi )∏ ij Фц (y i , Yj ) (1)

Z is the normalization constant. The likelihood function ф[ ( X[ , Yi ) is the local evidence of the node i . It represents the conditional probability that the observation node i takes the label Yi , which reflects the statistical dependence of x_t and Yi at the i position. The function ф[ ( X[ , Yi ) is modeled by a Gaussian mixture model. The formula is as Eq.(2).

Ф1 ( X[ ^, Yt )=ln P ( X[ | Yt ^, e )= ⁿ{√2 =. ехр{- ⁽ ' ₂ - ; ⁾ - }}=

• - 4 ⁾ -ln√2 ^Kal (2)

9 =(A^i, ^i , Ц2 , ^a2 ,⋯, ^l , °l ), where M-l and a^ are the class l mean and variance of GMM respectively. The potential function Фц ( Yt , Yj ) is the state transition matrix between pair nodes ( i , j ) , and is used to measure the similarity between neighboring nodes. In this paper, фц ( Yt , Xj ) is defined as a Potts model. The model is as follows:

0 Yi = Фц ( Yi , Yt)={P Yi ≠ Yj , where p is a parameter greater than 0.The model indicates that the adjacent objects tend to take the same label value in image segmentation.

Under the MRF-MAP framework, the MAP problem is equivalent to the minimization of energy to analyze image clustering in this paper. We make full use of the spectrum, color and texture features of the image object and a priori knowledge. According to the optimal criterion of statistical decision and estimation theory, the optimal segmentation and its corresponding scale problem are determined.

• B.    Multiscale Image Segmentation MRF Model Based on BP

The MRF model is suitable for the inference of the global probability, and the local information of the image is transmitted to the whole image step by step. In practical application, the pixels and objects are taken as nodes, and the energy function is constructed according to the features of the image and the spatial structure relationship. Then the optimal solution of the energy function is solved to extract the object information. In the process of solving the specific energy function, the optimization techniques are often used, such as simulated annealing, Gibbs sampling and graph cutting and so on. However, with the increase of the order of clusters, the computational complexity of the energy function will increase exponentially.

Belief Propagation (BP) is an efficient inference algorithm, which updates the current status of the entire Markov random field by using the mutual information between nodes and nodes. It is not only an approximate calculation method based on MRF model, but also an optimization algorithm. Each node in the network estimates its probability value by exchanging information with neighboring nodes, as shown in Fig.2. The computational complexity of this approach is linear [12].

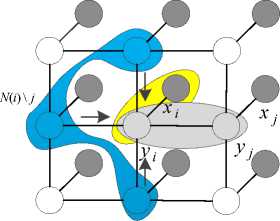
Fig.2. Belief propagation diagram

The formula of standard BP algorithm is т ц (уО = кЪхф (xl,ydiplj(yl,yj')nkeN(t)\jmkl(yd. (3)

The formula of computing confidence is bt(Уд = кфдуд Пуемсо тп(уд .        (4)

тц is the message passed from label node i to label node j , which represents the effect of the label node j on the current state of the label node i ; k is a normalized constant; NQWj denotes all neighborhood nodes of node i , but not node j ; b(yd expresses the approximate marginal posterior probability of node i .

The process of computing the confidence is to find a point and its adjacent nodes randomly, to compute the message sent to the neighboring nodes, and to calculate the confidence of the neighboring nodes. Then a point is randomly found, and the above process is repeated. Each iteration is computed on the basis of the previous iteration.

According to the message updating rule and the confidence formula, each b(y ) can be arbitrarily initialized, then m^ and b(y ) is solved iteratively until convergence. Finally, the corresponding probability can be computed from the confidence. The confidence level of a node is calculated by the belief propagation algorithm, which is its marginal probability distribution. This iterative method is easy to realize by computer programming, and is advantageous to parallel operation and improve the computing speed.

In image analysis and processing, the node information of the standard BP algorithm is usually defined by the confidence of a single pixel, which is iteratively propagated through nodes of MRF model. The computational complexity of this algorithm is O(TL²N), where T is the number of iterations of BP algorithm, L is the label space, and N is the total number of nodes of MRF model. Therefore, the inference of BP algorithm takes a long time in large scale images.

In this paper, the object-oriented BP algorithm takes the region as an object and uses the local region information of the image instead of the pixel information in the standard BP algorithm. Compared with the standard BP algorithm, the algorithm uses more regional information, so it has more local information in the process of message passing. Compared with the single pixel MAP segmentation criterion, the robustness of the local region information effectively reduces the influence of the image noise or texture mutation on the image segmentation results. Therefore, the multi-scale BP algorithm proposed in this paper converges faster than the traditional BP algorithm.

From Eq. (3), in the l -th layer, the iterative algorithms for computing the message of the multi-scale BP are as follows:

м(уМ = к ^ Ф®МФ®(уа П ^m«" ^1)(Уш) (ij)e о) keN(to\\to'

в®(у«д = к ^ ФцЧу^Ф^Чуд П ^M(toyJ (i j)e to k eN)to")

Eq. (5) is a message update formula based on hierarchical BP algorithm. In the formula , M®(y_to ' ) is the message in the l -th level, which is transmitted from the object node y _и to its neighbor y _и - . П кем(о>)\ и¹ М^" ¹⁾ (Уо>) is the local object message collected by object node y_k in the ( l -1)-th iterative operation; keN(to)\to ' is that the object node k belongs to the neighborhood region of object node to, which region does not include the object node to ' . Eq. (6) is the confidence updating formula of the object node y . i n the formula,

⁽⁾( ) is the confidence of the object node y in the l -th level, and κ is the normalization constant.

In the image clustering analysis based on objects, the label of the object node y is estimated by the object confidence B()(y ) according to the MAP criterion, which is

= ⁽⁾ ( ). (7)

In this paper, the minimum scale ground object of the image is obtained according to the watershed transform algorithm. Multi-scale MRF model based on BP is used to extract the objects on each scale image, and multi-scale segmentation results can be obtained. There is a causal relationship between the segmentation results at different scales. Objects on a large scale are the result of merging multiple small scale objects, that is, large-scale image feature is a simplified small-scale feature.

• III. Automatic Extraction Algorithm on the

Optimal Segmentation Scale

• A.    Image Preprocessing

The algorithm proposed in this paper is a kind of hierarchical clustering algorithm. Starting from the initial regions computed by the watershed transform algorithm, the bottom-up region merging method is used to form polygonal objects at different levels (scales).The watershed segmentation algorithm is a mathematical morphology method which uses pixel gray value to mark the image region. Suppose the digital image f is defined as the gray scale image on d, h and h are the maximum and minimum values of the gray scale image respectively, and the watershed transform is carried out from the minimum value to the maximum value according to the gray level. In this paper, watershed transform algorithm in discrete domain is used, which is defined as

X h mn =^{ P ^S Dlf ( P ) = ^h '  ^} = T h mn

X h + 1 = MIN h + 1 ^U IZ T^ _t ⁽ X h ), ^h S [ h mjn , h max )

In the above formula, refers to the set of all water basins in the gray level h when the water basin is expanded, all pixel sets with gray level less than h level are denoted by ={ ∈ | ()≤ℎ} , and IZ is the geodesic influence region. From the Eq. (6), all pixels that do not belong to the water basin are likely to be assigned to one basin in X at gray level h. Thus, the above definition allows a pixel which gray level is not greater than h and does not belong to any of the water basins in to be merged with the water basin in . At a certain iteration, if the distance from a pixel to at least two nearest water basins is equal, the pixel is temporarily labeled as a watershed pixel. However, the pixel may be merged into other water basin in the next iteration. Therefore, only when all the pixels are processed, the pixel labels are determined.

From the definition of watershed transformation algorithm, it has the advantages of simplicity and high speed, and can detect the weak edge object and obtain the complete boundary of the object, which is widely used in various fields. However, the gradient image is usually transformed, so the algorithm is affected by dark noise and other factors. There is a large number of pseudo local minima in the segmentation results, and there will be over segmentation. In particular, high resolution remote sensing images with rich texture information are prone to over segmentation. Because all regions with the same label are homogeneous and uniform in the over segmentation image, the region can be merged according to similarity. In this paper, the over segmentation image applied by the discrete domain watershed algorithm is used as the finest granularity (scale) segmentation image.

• B.    Optimal Segmentation Scale Extraction Algorithm

In this paper, the bottom-up merging strategy is used to obtain the multi-scale image segmentation. Firstly, the object information in the neighborhood is transmitted with each other in the finest scale image. Then, the similarity between objects is computed to merge objects. The result of object merging produces a larger scale image. Repeat the above process, the network hierarchy can be built. After each merging, each small scale region records the adjacent large scale objects and adjacent objects.

For optimal segmentation scale extraction algorithm of multi-scale MRF model based on belief propagation, the specific steps are as fellows.

Input: the original image;

Output: the optimal segmentation scale image and the optimal segmentation scale parameter c .

• 1)    Use the watershed transform algorithm to obtain multiple homogeneous regions (objects) of the remote sensing image, and take the segmentation result as the smallest scale image;

• 2)    Extract the feature values of the spectrum, color and texture of the object in the previous step; compute mean and mean variance deviation of the brightness of each object in the image; compute the color feature values for each object in the image; use two-dimensional Gaussian kernel function to compute the energy of the object in different directions; compute the texture feature value of the object by a Gaussian difference filter.

  g ( t ) =

  
  

  A e t 2 2 - 2 427га,²

  
  

  B e t 2 /2 " 2 4 2 n— 2

  
  

• 3)    Compute the joint likelihood and use the expectation maximization algorithm to estimate the GMM parameters (    ,    ,     ).

• 4)    For 1= L to 0 execute step 3 and step 4:

• i)    According to Eq. (4) and (5), the object message is iteratively transmitted between the MRF nodes in the

l -th layer until the global probability converges. That is

• ii)    According to the MAP criterion, the estimated value of object label is

У™^АР = arg_ymax5™(y „ ).

• 5)    The standard BP algorithm is run in the finest level image, and then the iterations are performed by Eq.(2) and (3) until convergence. According to the MAP criterion, the estimated value of each pixel label is

у М^др _ arg ^ maxft ⁽¹⁾(y ₍).

• 6)    Compute the posterior marginal probability of all the objects between hierarchy, and choose the maximum value to determine the optimal segmentation scale image and its corresponding optimal scale parameter.

  

  (c) c =0.075

  
  
  

  (d) c =0.085

  Fig.3. Multi-scale Aerial Image Segmentation

  
  

• IV.    Experimental Results and Analysis

• A.    Multiscale Image Segmentation

In order to verify the effectiveness of the proposed method, the experimental data are used for aerial images and IKONOS images, shown in Figure 3(a) and Figure 4(a). The size of aerial image is 300×500, which mainly includes residential land, roads, trees, water, farmland and so on. IKONOS image is panchromatic image, which spatial resolution is 1m. The size of the image is 514×254, which consists mainly of houses, trees, roads, bushes and other types. The multiscale segmentation results of the proposed algorithm are shown in Figure 3(c-d) and Figure 4(c-d). c is a segmentation scale parameter, its value range is [0,1].

(a)

(b) c =0.042

(a)

(c) c =0.078

(b) c =0.065

(d) c =0.084

Fig.4. Multi-scale Segmentation of IKONOS Image

The results of the minimum scale segmentation of the two images are shown in Figure 3 (b) and Figure 4 (b). As can be seen from the figures, some of the original integrity of the region is divided into a number of different regions. There are obvious over segmentation phenomenon, resulting in the region of false segmentation. With the merging of regions, the phenomenon of over segmentation in some regions is gradually disappearing. As shown in Figure 3(c), when the scale parameter c is 0.075, farmland and bare land is divided relatively complete. Compared with the image of the scale parameter c =0.065, the over-segmentation phenomenon can be eliminated in the housing area. However, with the increase of regional mergers, some areas have also appeared the phenomenon of less segmentation.

For example, the lower right corner of the forest land and the adjacent grassland is divided into an area in the image scale parameter c =0.085. The situation in Figure 4 is similar to that shown in Figure 3.

With the combination of regions, the phenomenon of over-segmentation is gradually reduced. When the value of the scale parameter increases to a certain value, there will be under-segmentation phenomena in some areas.

In the above segmentation results, with the increase of the region merging, the size of the object in the result of the segmentation is also increasing, and the objects on the large scale are collections of objects on a small scale. It can be seen that, in the early stage of regional merger, the similarity of the regional objects is stronger in the finest scale image. With the regional merger, the region becomes larger and the regional heterogeneity increases. However, the value increases gradually and then decreases gradually with the increase of the segmentation scale by computing the posterior marginal probability of the object in each scale. By computing the extreme value of the variation, the segmentation scale parameters 0.075 and 0.078 are respectively taken as the optimal segmentation scale parameters of the above aerial image and IKONOS image.

• B.    Experimental Results and Analysis

In order to analyze and evaluate the effect of image segmentation, this paper introduces the Performance Evaluation of Tracking and Surveillance (PETS) method. Based on the measurement method of PETS, the degree of mismatch between pairs of scanning points is measured by comparing the true sample segmentation (manual segmentation) and the detection of samples (algorithm segmentation), which is called the Negative Rate Metric (NR) [13]. That is

NR = 1( NR fn + NR fp )

where the formula

NR _fn

^N fn indicates that the

Ntp + N> number of real samples that are not detected accounts for the proportion of all “real samples”; The amount of data mistaken for the real sample in the observation accounts for the proportion of all real samples. The ratio is called by error rate.

The formula         Nfp indicates that the number fp  Nfp + Nn of non real samples is proportional to all the non real samples, that is false negative rate.

The experimental data can be divided into two types: aerial image and IKONOS image, the number of which is 30 and 50 respectively. Using the algorithm proposed in this paper, these two kinds of images are segmented by optimal scale. The experimental results are statistically calculated by formula (9). The comparison between the segmentation results of the optimal segmentation scale and the manual segmentation results is shown in Table 1. The error rate, false negative rate and mismatch in Table 1 are the mean values of the corresponding data subsets, respectively.

Table 1. Segmentation Evaluation of Our Algorithm

Image	Error Rate	False Negative Rate	Mismatch
aerial image	0.001812	0.1232	0.0625
IKONOS	0.004506	0.1041	0.0543

It can be seen from Table 1 the error rate, false negative rate and mismatched degree by our algorithm are very small, which are very close to the result of artificial segmentation. The algorithm is compared with the standard BP algorithm on the processing time.

An aerial image and IKONOS image with a size of 300×500 were processed respectively, and the results are shown in table 2. The proposed algorithm has faster convergence rate, and the optimal segmentation scale factor can be obtained automatically.

Table 2. Comparsion with Our Algorithm and Standard Bp Algorithm

Algorithm	Iteration Times		Runtimes(s)
	Aerial Image	IKONOS	Aerial Image	IKONOS
Standard BP Algorithm	31	26	12.314	9.562
Our algorithm	16	11	9.106	6.781

Experimental results and comparisons show that the proposed multiscale BP algorithm converges faster than the traditional BP algorithm. This is because the standard BP algorithm uses the pixel as the unit of message transmission; the method of this paper uses the object to carry on the message transmission directly, which avoids the misclassification and error merging of the pixel. At the same time, the size of different local objects can get the message of different scales. Therefore, it can effectively reduce the problem of slow message passing in long distance pixels, and improve the computing speed. Therefore, the problem of slow message passing over long-distance pixels is reduced by the large-scale message, and the computation speed is improved.

• V.    Conclusion

In this paper, a multiscale BP algorithm based on MRF model is proposed, which is based on the bottom-up approach, and the hierarchical structure is established to extract the optimal segmentation scale of high resolution remote sensing image. The algorithm introduces the watershed algorithm to divide image into a number of homogeneous and uniform regions. The local regions are regarded as the object nodes. Then, the feature information is transferred between object nodes in the same level and between different levels. The neighborhood object nodes with similarity maximum are merged. Therefore, the global optimal segmentation scale selection can be realized automatically. Compared with the traditional BP algorithm, the proposed method can effectively avoid the subjectivity and unilateralism of the segmentation process, and improve the accuracy and efficiency of the high resolution segmentation.

Acknowledgment

This work is funded by the National Natural Science Foundation of China under Grant No.41301371 and funded by State Key Laboratory of Geo-Information Engineering, No. SKLGIE2014-M-3-3.