A New Efficient Reordering Algorithm for Color Palette Image

Published Online November 2013 in MECS

There are various image compression schemes for different kinds of image characteristics. For an image that comprises a small amount of colors for a large color space, the palette-based (or color-mapped based) compression method often provides good efficiency. This kind of compressed image consists of two different parts. One is the fixed lookup color table. That is the color collection for the image. Another is the index sequence of pixels to indicate the color’s position in the lookup color table. Many lossless compression algorithms adopt a differential predictive approach to decode the index sequence. Most prediction schemes assume that neighboring pixels have similar intensity. We can infer that if the index sequence is smoother then lower predictive error can be obtained. On the contrary, the higher predictive error may occur while the index sequence is variable. To maintain a smooth index sequence, and to make sure the higher compression ratio and lower predictive errors, the color re-indexing problem is raised[1].

The importance of palettized format is also apparent from the large number of commercial software products [2]. Palette images have two typical elements: a palette table which provides for the translation between an index value and its associated red, green and blue intensity values, and an index image which contains the index value for each pixel in the image [2,3]. A viewable image is created from a palette image by replacing each index with its palette table entry, whose size is the sum of the sizes of the index image and the palette table.

The color re-indexing concept is to reorder the lookup color table. Different index sequences are generated by using the color re-indexing procedure. Difference index sequences imply different predictive errors. To reduce the predictive errors, the variableness of index sequences must been reduced in advance. Therefore, the color reindexing problem also can be treated as a smoothness maximization problem [1].

However, the compression of color-indexed images is a challenging task to most general purpose continuous-tone image coding techniques due to the loss of correlation between index pixels as a result of quantization. Reindexing addresses this problem by permuting the indices to yield a more compressible index image without losing any information, as the color palette table changes accordingly. This local index redundancy can be considered to improve the compression performances of any compression technique as the size of the image is dominated by the index image [1,2]. The method is also costless in terms of side information as they do not require any post-processing[2].

The bottleneck of this solution is the intrinsic inefficiency to numerically optimize the palette reindexing. If the optimal palette configuration is sought, the computational complexity involved would be high. As a matter of fact, a table of M colors corresponds to M! configurations [1,2,3]. Clearly, this exhaustive search is impractical, and thus transforms to an NP hard problem. Thus, the only strategy to avoid the exponential resources is to adopt some suitable heuristic [4,5,6].

In this paper, we introduce a heuristic method to reindexing is proposed aiming to relatively reduce the computational complexity of previous works. The results indicate that the proposed approach is very effective.

The paper is structured as follows. Section 2 describes the Related work in this field and Section 3 introduces the Reindexing problem. The proposed method is shown in Section 4. Experimental results are presented in Section 5. In Section 7, conclusions are drawn.

• II. Related work

The existing solutions to the re-indexing problem can be classified into two groups, according to the strategy adopted. The first group of solutions performs the reindexing of color indexes according to perceptive similarity between different colors. Spira et al. [4] proposed a reindexing scheme in which the colors were ordered according to the distances between them in threedimensional color space, based on the assumption that image objects are constructed from pixels with similar colors using the Farthest Insertion Algorithm, with O (M3) complexity. The second group of algorithms rely only on the statistical information conveyed by the index image to perform the reordering operation, guided by both information theory and local adaptive considerations. Memon et al. formulated the problem of palette reordering within the framework of linear predictive coding [4,7] well modeled by a Laplacian distribution formulated as the optimization version of the linear ordering problem with O(M4) complexity. The palette re-indexing method proposed by Zeng et al. [1] is based on one-step look ahead greedy approach. The algorithm starts by finding the index that is most frequently located adjacent to other (different) indexes, and the index that is most frequently found adjacent to it. This pair of indexes is the starting base for an ordered set, S, that will be constructed, one index at a time, during the operation of the re-indexing algorithm. New indexes can only be attached to the left or to the right extremity of the ordered set. The computational complexity is O(M3). Battiato et al. [4,7,8] proposed a greedy strategy based on sequentially selecting the best edge still not processed, i.e. the one with the largest weight. The methodology tends to smooth the relative transitions in the indexed image, solving in an approximate way a related optimization problem over a weighted graph with O(M2 log M) complexity. Recent works in this field have concentrated on the application of soft computing algorithms to the reindexing problem. Chang et al. proved that it is possible to achieve high compression with acceptable image quality using the topology-preserving property of selforganizing Kohonen feature map [4,9] which considers “1D string neural structure” wherein, the neuron closest to each fed training vector, called the “winning neuron”, will update itself while the neighboring neurons will update according to the neighboring function and gain function. The training vectors are extracted from the image using the butterfly-jumping sequence which leads to fast-converging training. Rundo et al. suggested a Motor Map Neural Network based re-indexing that uses an unsupervised, application independent, highly adaptive learning algorithm called “Winner-take-all” learning driven by the reward function [8].

In this paper, we present a heuristic method to achieve relatively fast and optimal global convergence.

• III.    The Color Re-indexing Problem

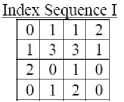
Many commercial image processing and geographic information systems adopt the color mapping system to represent color images and save storage space at the same time. In the color mapping system, a fixed lookup table is generated in advance to record the relationship between the colors and indices. Then indexed images (also called index sequences) encode colors using the fixed lookup color table. Each entry in the color table is generally a triple of RGB values. For each pixel in an image, only the indices of corresponding colors need to be stored. Fig. 1(a) shows an example of a simple image with pixels. The entry in each square is a triple of RGB values for the corresponding pixel. To represent the encoded result of color mapping system, a lookup table I and an index sequence I for the example image (shown in Fig. 1(a)) are presented in Fig. 1(b). In Fig. 1(a), the first entry of RGB values is (100, 20, 50); therefore, the first index value of index sequence I is “0” by looking up the lookup color table I[1].

• (100.20.50)    (60,150,200)  (60.150.200)   (140,140,120)

• (100.20.50)   (30,70.80)    (30,70.80)     (60,150.200)

• (140.140.120)    (100,20,50)   (60.150.200)   (100.20.50)

• (100.20.50)    (60.150,200) (140.140,120) (100.20.50)

• (a)    An example image

Lookup Color Table I

0: (100,20,50)

1 (60.150.200)

2: (140.140.120)

3: (30.70,80)

• (b)    A lookup table I and an index sequence I

Lookup Color Table II 0: (140,140,120) 1: (100,20,50) 2: (30,70,80)

3: (60,150,200):

Figure 1. An example of color mapping system using a lookup color table with different orders[1]

If we reorder the indices of lookup color table I to generate lookup color table II, the corresponding index sequence of original image based on lookup color table II can be generated as index sequence II shown in Fig. 1(c). From Fig.1, we can see that different order of indices in the lookup table produces different index sequences for an image. Different index sequences could lead to different compression efficiency. Therefore, the efficiency of a lossless compression algorithm for indexed images may greatly depend on the assignment of indices in the relative lookup color table. To compress the index sequence, many lossless compression algorithms adopt a differential-predictive approach to encode the index sequence. Smoother index sequence is favorable for compression algorithms. An entropy measure [3] or a difference measure [4] can measure the distribution of an index sequence. We list a simple difference measure as follows[1].

т х #z - 1

W) = ^-^J

Where m X n is the size of a image and s i is the i th pixel in the image by raster scan order. In above case, if we apply Equation (1) for Fig. 1(b) and Fig. 1(c), we can get dissimilar values 16 and 22, respectively. It indicates the fact that lossless compression can be optimized by choosing a different platted ordering. Finding an optimal indexing scheme is a crucial step for different lossless compression of indexed images.

• IV.    The proposed method

We shall describe the details of the proposed algorithm for re-indexing problem in this section. Let I be an image of m × n pixels and M be the amount of distinct colors. There is a color lookup table { c0 ,c1 , … ,c_m-1 } and an index sequence { s0 ,s1 , … ,s_m×n-1 } used to represent the image I , when I is compressed by a color mapped algorithm, where ci is a color value and si is a color index of location i in lookup table. To further reduce the size of index sequence, a lossless compression technique will be applied. To make sure the efficiency of lossless compression technique can be achieved, we have to minimize the difference of neighbour indices. That means we have to re-arrange the order of indices in the color lookup table.

In this paper, we apply an heuristic method to find out the optimal re-indexing order. Our method consists of seven steps:

Step1: Encoding : The purpose of this study is to find a sequence of Colors for minimizing compression rate. Thus, each chromosome is sequence variety of Unique Color. Each Color is considered as a gene. Therefore, the best way to encode chromosomes is permutations encoding. To explain how chromosomes are encoded, consider that there are 8 Color, Ci represents the Colors(Fig 2).

CH1	C1	C4	C8	C2	C7	C3	C5	C6
CH2	C6	C1	C7	C3	C5	C8	C2	C4

Figure 2. two of solution encoded

Step2: Generate initial solutions: To start, should generate an initial random population for entry into the first generation. For this, a random generator function of chromosomes must be employed[4]. In order to create an initial population, we need Information on the all Colors of iamge. Random chromosomes generate the initial population.

Step3: Destruction: Select α positions from one sequence (Color map) at random without repetition and then remove α positions from the sequence.

Step4: Construction: Add α positions from the sequence obtained to end Destruction sequence. For example Consider six colors for color map in a image. We assume that the initial color sequence is (1, 2, 3, 4, 5, 6) and it is obtained randomly. The α_R and α_D are randomly obtained as (2, 4, 5) and (1, 3, 6), respectively. The Destruction and Constructive method is illustrated in Fig 3.

Step5: Calculate Fitness: The fitness function is calculated according to the (2) equation.

For each solution CHl , we can produce from S by CHl mapping where

. The best solution with the lowest value in the pool will be outputted as the winning solution, and the procedure is terminated.

Step6: Selection: The solutions are selected according to their fitness value. Once fitness values have been evaluated for all solutions, we select good solutions through Tournament strategy for next generation.

Step7: Stopping criteria: If an acceptable solution is achieved, so the algorithm stops else repeat from step 3.

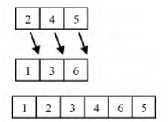
(a) Destruction

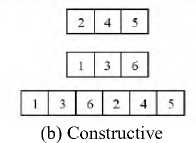
Figure 3. Destruction and Constructive [10]

Fig 4 shown the flowchart of our approach. Each part of flowchart described in above

Figure 6. Pepper

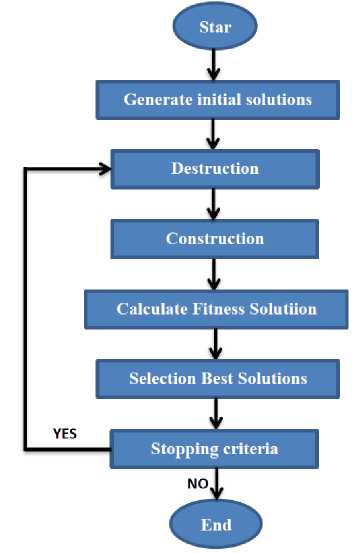
Figure 4. the flowchart of the proposed method

Figure 7. Sailboat

• V.    Experimental Results

To evaluate the effectiveness of the proposed method, we have performed several tests over different sets of indexed images and comparisons have also been carried out between our re-indexing algorithm and the methods described in [1] using Genetic Algorithms. All the programs were written in MATLAB and were run on a personal computer with the Windows 7 operating system. The CPU is Dual CORE with 2 GB Memory. In our experiments, six test images are processed into many copies of color-mapped images with two different numbers of colors, such as 64 and 16 different colors and size is 256x256. Six color-mapped images with 64 colors are shown in Fig. 5, 6, 7, 8, 9 and fig 10.

Figure 8. F16

Figure 9. Baboon

Figure 10. Snow

Figure 5. Lena

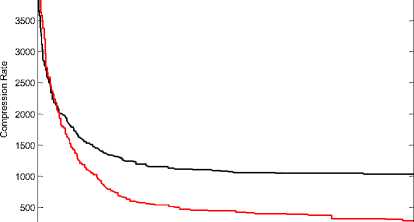
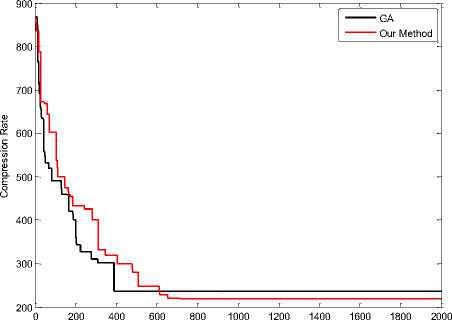
It is noted that the values of difference measure those with our proposed scheme are decreasing compared with those with GA [1] color mapping. This reduction indicates the efficiency of our proposed re-ordering scheme. results of simulations when colors equal with 64, shown in Fig 11, 12, 13, 14 and 16.

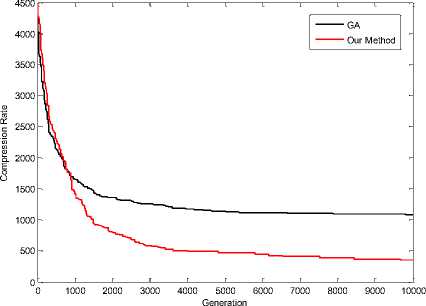
Figure 11. Compression Rate in Lena Image (64 Colors)

GA

Our Method

1000   2000   3000   4000   5000   6000   7000   8000   9000   10000

Generations

Figure 12. Compression Rate in Pepper Image (64 Colors)

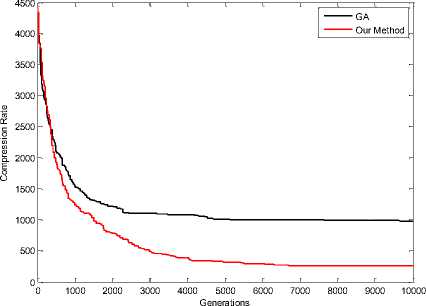
Figure 13. Compression Rate in Sailboat Image (64 Colors)

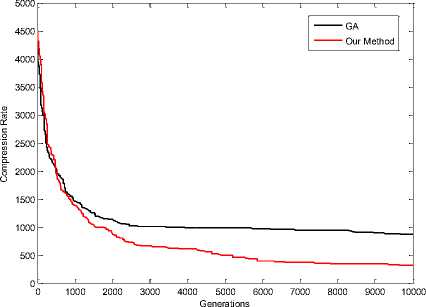
Figure 14. Compression Rate in F16 Image (64 Colors)

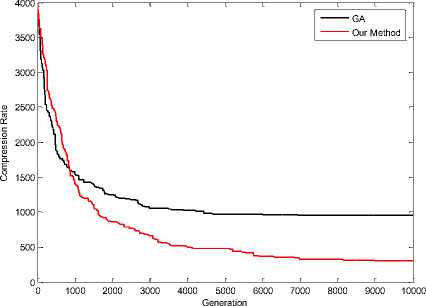
Figure 15. Compression Rate in Baboon Image (64 Colors)

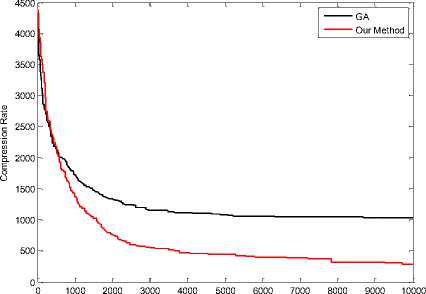
Generations

Figure 16. Compression Rate in Snow Image (64 Colors)

Fig 17, 18, 19, 20, 21 and 22 shown results of simulations when colors equal with 16. These results shown effectiveness of the proposed scheme. Red Line in figures shown our method and black line shown GA method for Re-indexing. The vertical axis represents the compression rate and the horizontal axis represents the number of generations.

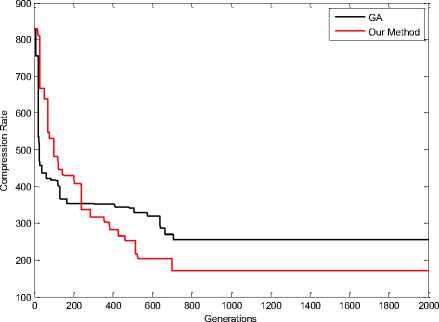
Figure 17. Compression Rate in Lena Image (16 Colors)

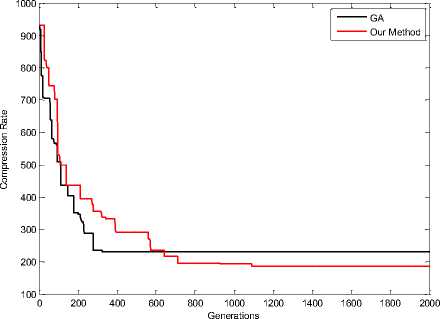
Figure 20. Compression Rate in F16 Image (16 Colors)

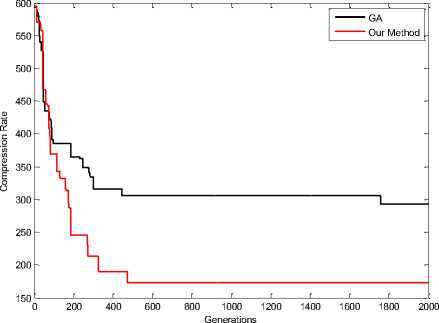
Figure 18. Compression Rate in Pepper Image (16 Colors)

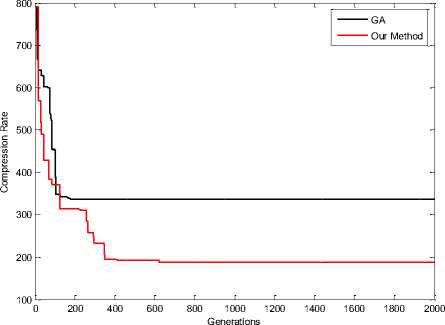
Figure 21. Compression Rate in Baboon Image (16 Colors)

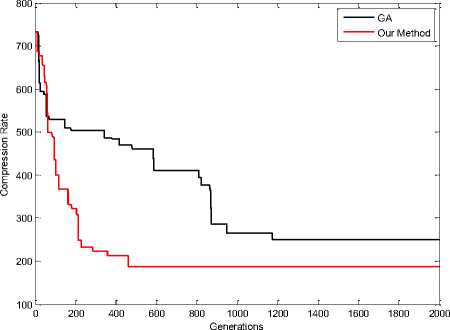
Figure 19. Compression Rate in Sailboat Image (16 Colors)

Generations

Figure 22. Compression Rate in Snow Image (16 Colors)

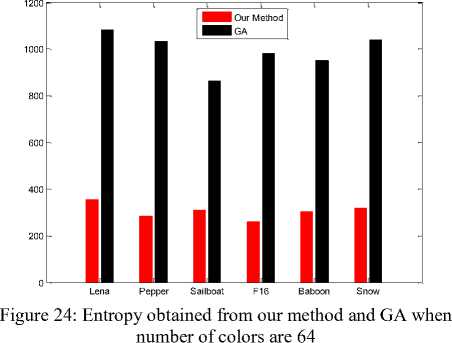
Entropy obtained from our method and GA shown in table 1 and Fig 23, comparison together when number of colors are 16. Entropy obtained from our method and GA when number of colors are 64 shown in table 2 and Fig 24, comparison together .According to table 1 and table 2 our method results is better than GA results.

TABLE 1: Entropy obtained from our method and GA when number of colors are 16

Images	Our Method	GA
Lena	171	255
Pepper	173	293
Sailboat	188	250
F16	186	231
Baboon	187	336
Snow	200	345

TABLE 2: Entropy obtained from our method and GA when number of colors are 64

Images	Our Method	GA
Lena	356	1083
Pepper	284	1034
Sailboat	311	866
F16	262	982
Baboon	305	952
Snow	318	1041

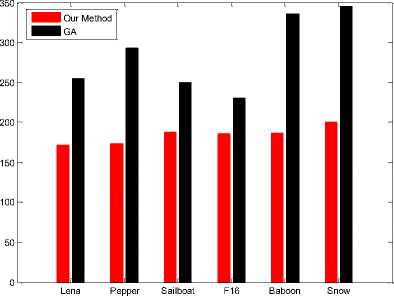
Figure 23. Entropy obtained from our method and GA when number of colors are 16

zero-order entropy value. The results indicate that the proposed approach is very effective, acceptable and proved in comparison with GA.