A New Heuristic Approach for DNA Sequences Alignment

Published Online November 2015 in MECS

DNA (deoxyribonucleic acid) and RNA (ribonucleic acid) play fundamental roles in carrying genetic information in all living things on Earth. These structures are double helixes that look like a twisted ladder in which the rungs of the ladder consist of match pairs of nucleobases [1, 16]. DNA and RNA have great chemical similarities. In their primary structures both are linear polymers (multiple chemical units) composed of monomers (single chemical units), called nucleotides. Cellular RNAs range in length from less than one hundred to many thousands of nucleotides. Cellular DNA molecules can be as long as several hundred million nucleotides [2] (Fig.1). The term DNA sequencing encompasses biochemical methods for determining the order of the nucleotide bases, adenine, guanine, cytosine, and thymine, in a DNA oligonucleotide. The sequence of

DNA constitutes the heritable genetic information in nuclei, plasmids, mitochondria, and chloroplasts that forms the basis for the developmental programs of all living organisms. Determining the DNA sequence is therefore useful in basic research studying fundamental biological processes, as well as in applied fields such as diagnostic or forensic research. Because DNA is key to all living organisms, knowledge of the DNA sequence may be useful in almost any biological subject area. For example, in medicine it can be used to identify, diagnose and potentially develop treatments for genetic diseases. Similarly, genetic research into plant or animal pathogens may lead to treatments of various diseases caused by these pathogens [3].

Fig.1. DNA Helix

In comparative genomics, comparing genome sequences is one of the main tasks because sequence similarities strongly reflect the evolutionary relationships between the corresponding species. In addition, with the introduction of next-generation sequencing technologies, the demand for rapid comparisons of massive amounts of long sequences has increased in recent years [4,5-11,15]. Improvements in the efficiency of DNA sequencing have both broadened the applications for sequencing and dramatically increased the size of sequencing datasets. For years, DNA comparison has been used in biology and forensics to discriminate and compares genes or genomes. Those tools vary in size, complexity and functionality based on several factors. Some small tools or websites are developed as free or open source for research or experimental purposes. Examples of such small size limited purpose tools or applications are: Double Act , Genomatix     ,     Mobyle

, ALIGN, FASTA, etc. BLAST: (Basic Local Alignment Search Tool) [12,13] is an example of a larger scale. Most of these algorithms uses Smith–Waterman algorithm for performing sequence alignment. This algorithm which is also used in crimes’ forensic investigation does not use full DNA to DNA sequence comparison. It rather selects several segments (e.g. eight segments) selected from the different locations of the DNA. BLAST uses also dynamic programming and “seeding” to find starts of possible matches. The goal is to accelerate the process of finding matches between DNA sequences as this can take a significant amount of time and resources. Another process that can be different from one tool to another is the ranking of the different matches. This can particularly occur when more than a match is in the same size [12,17].

The current paper addresses the problem of finding a sequence alignment between two DNA sequences, in which individual similar letters from each sequence are placed into correspondence. It is based on a heuristic approach including three processing phases: the first phase finds the longest common substrings in the two sequences, the second one sorts the obtained common substrings descending according to their lengths, and the last phase generates the optimal two aligned sequences.

The rest of the paper is organized as follows. Section II discusses the suggested algorithm. The implementation and experimental results are discussed in Section III. The work done in this paper has been concluded in Section IV.

• II.    The Suggested Approach

The aim of the suggested algorithm is to align homologous regions separately keeping their order in both DNA sequences.

Given two DNA sequences:

X= x _ (0) x _(1) x_(2)…….x_(m-1)       (1)

Y= y_(0) y_(1) y_(2)…….y_(n-1)        (2)

Where X, Y are two sequences of length m-1, n-1 respectively, and x_i and y_i are chosen from a finite alphabet A, e.g. {A, C, G, T}:

x_i ∈ {A, C, G, T}, y_i ∈ {A, C, G, T} (3)

The goal is defining the distance between the sequences X and Y, or alternatively their similarity. Where similarity is defined with reference to a sequence alignment, in which individual letters from each sequence are placed into correspondence. Achieving this goal, the suggested approach has been divided into three consecutive modules:

Module I: An algorithm for finding all common substrings between two sequences and it has previously published [14, 18]. In this module, two DNA sequences are compared to find all possible identical matches between them. It is based on the convolution between the two sequences.

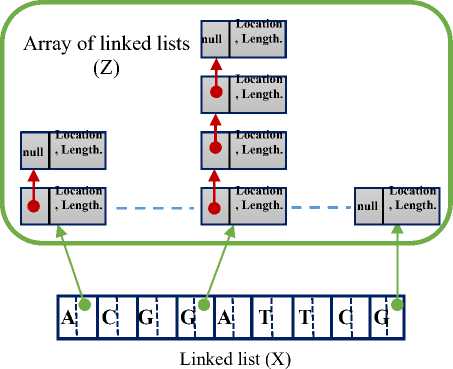
The data structure required for the suggested algorithm is shown in Fig.2. The major DNA sequence string is represented in the linked-list X while the minor one is represented in circular linked-list Y. Each element of the linked-list Y contains a data filed in addition to a single directional pointer to the next element in a circular manner. Each data field of Y holds one of the minor DNA sequence characters. Each element of the linked-list X consists of three fields described as follows. The first one is a data field holding one of the major DNA sequence characters. The second field is a pointer to an independent linked-list, where the collection of those independent linked lists are grouped and considered as array of linked-list Z. The array Z will be dedicated to hold the resultant of the matching algorithm as will be illustrated later. The third filed is simply a pointer to the next element of the linked-list X.

C

G

T

A

T

C

C

-------►

Circular linked list (Y)

• Fig.2. The Data Structures used in the Suggested Approach

The matching algorithm aims to determine both the location and length of all possible common substrings between the two DNA sequences represented in X and Y linked lists respectively. The main matching algorithm and its subroutines are listed in List. 1 through List.3.

Referring to List. 1, when the two variables x and y are equal, the process named Get_substring_until_no_match (List 2) will be performed continuously reading new pair of characters as long as the new pair of characters x and y are equal otherwise the process terminates. The length and location of the obtained substring are considered as input to the process named Add_obtained_substring_ to_Z (List 3).

List.1: Pseudo code of Matching Algorithm

// Input: DNA1 and DNA2 sequences

Get Length_of_DNA1;

Get Length_of_DNA2;

For I = 0; I < Length_of_DNA1

For j = 0; J < length_of_DNA2

x = read character from DNA1[I]

y = read character from DNA2[J]

if ( x == y)

{

Perform Get_substring_until_no_match(I,J);

// L = length of the obtained substring

Add_ obtained_substring_to_Z(I,J, L);

}

Next J;

Next I;

List.2: Pseudo code Get_substring_until_no_match

Input: I, J m =I;

n = J;

Length =0;

do

{ x = read character from DNA1[m] y = read character from DNA2[n] Length ++;

m++;

n++;

} while (x == y)

Return Length

List.3: Pseudo code Add_obtained_substring_to_Z

Input: I, J, Length m =I;

n = J;

l = Length;

if X[m].pointer == null

{ create new linked_list Z[m]

add new cell with ( n, l )

// n = location of substring in DNA2 sequence

// l = length of substring

}

Else

Add new cell to linked_list Z[m]

The Add_obtained_substring_to_Z process is responsible of adding information related to the obtained substring to the array of linked lists Z. Each character of the major DNA sequence, which is represented by X[I], points to a separate linked list in the array Z. The initialization process does not create the linked lists in array Z but leave this task for process Add_obtained_substring_to_Z to create only the actually needed linked lists to save the allocated memory space. Each separate linked list Z[I] should hold information about all common substrings between sequence X, starting at position I, and sequence Y. Accordingly, the process adds a new node to the corresponding linked list Z[I] writing both the length of the substring (Length), and its location (J) in the second sequence Y to the corresponding fields of this node.

By the end of the matching process, some characters of the DNA sequence X have linked lists in the array Z and the others do not have.

The following example illustrates the matching process of the suggested algorithm:

Input: two sequences:

DNA-1 sequence = “ATCAGTTACGT”

DNA-2 sequence = “TATCATG”

The two sequences are placed in linked lists X and Y respectively. The matching process yields the array Z of the linked lists (Red boxes in Fig.3). For example, the first character at position 0 of the first sequence (“A”) has two matches with the second sequence at locations 1 and 4 with lengths 4 and 2 respectively. The first matching has length of 4 where the substring “ATCA” exists in both sequences. The second matching has length of 2 where the substring “AT” exists in both sequences.

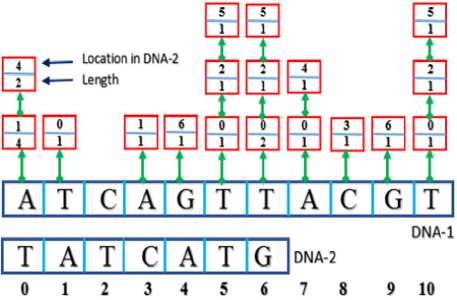
Fig.3. Illustration Example of the Matching Process

Inspecting the linked lists produced by the matching process leads to finding that the longest common substring is “ATCA” at location 0 of the first sequence and location 1 of the second sequence.

Module II: Module I generates a list of the common substrings between DNA sequences X and Y along with their lengths and their locations in both X and Y sequences. In Module II, this list is sorted descending according to the lengths of the obtained common substrings, location in X and location in Y respectively.

Module III: the algorithm of this module attempts to infer which positions within both sequences are homologous. The output of module II is passed as input to this module where individual letters from each DNA sequence are placed into correspondence. To explain the algorithm behind module III let us begin with the following example:

Sequence-1:

GAATTCAGTTACGGTAATCGTTACGACGTAATCAGTATCAGT

TACGA

Sequence-2:

GGATCGAAGCTCGATCGTTACGACGTGGCACCATCGT

Applying module I to both sequences yields several common substrings and sorting these substrings (applying module II) yields the list partially shown in Fig.4.

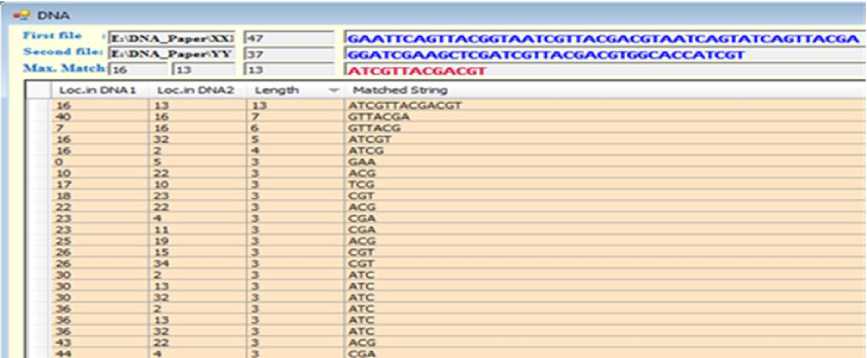
Fig.4. Sorted List of the Common Substrings According to Module II

We can geometrically (Fig.5) represent any common substring S with length l as:

S = {(x1, y1), (x2, y2)}               (4)

subject to the following condition: if two substrings belong to the same sequence, we choose both of them if and only if the following four conditions are satisfied and assuming that S1 is longer than S2 :

Where:	S2.	. x1	∉ [S1.x1, S1.x2],	(7)
x1 = position of the substring in the first sequence X y1 = position of the substring in the second sequence Y	S2.	. x2	∉ [S1.x1, S1.x2],	(8)
x2 = x1 + l                    (5)	S2.	. y1	∉ [S1.y1, S1.y2],	(9)
y2 = y1 + l                   (6)	S2.	. y2	∉ [S1.y1, S1.y2]	(10)

Considering pair of the common substrings in the current example:

The first one is “ATCGTTACGACG” has length 13 and starts at position 16 in the first sequence and at position 13 in the second sequence. Geometrically, we can define this substring as: S1{(16,13),(29,26)}. The second one is “CGTTACGA” with length 7 and starts at position 40 in the first sequence and at position 16 in the second sequence. And can be defined geometrically as: S2 {(40, 16), (47, 23)}. So, We have two choices of alignment; either “ATCGTTACGACG” of the first sequence with its correspondence in the second sequence or “CGTTACGA” of the first sequence with its iGAAnCAGTTACGGT^^TCGnACGACGTMTCAGTATCA^TTACG^

GGATCGAAGCKI^U jHACG/^G^GCACCATCGT correspondence in the second sequence. However, we cannot make alignment of both of them, as the second substring is included in the first substring of the second sequence. To avoid this conflict the choice should be

Or simply omit all substring in zone A and zone B as illustrated in Figure.5.

Applying the last rule to the sorted list of common substrings in the current example yields the short list shown in Fig.6.

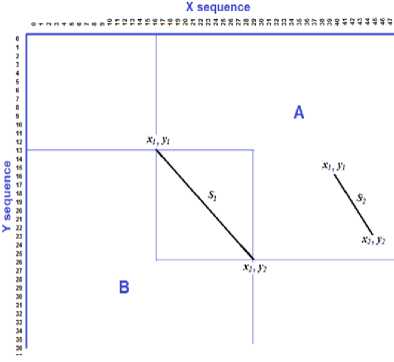
Fig.5. Geometrical Representation of Common Substrings

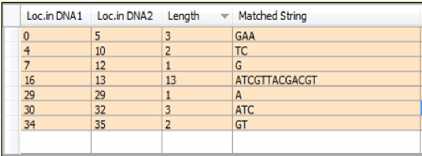
Fig.6. Short List of the Common Substrings

for (int i = 0; i < x - y; i++) temp = temp + "=";

}

}

The first phase of the alignment algorithm is listed below.

The input to this phase is the short list previously obtained (Fig.6). It is based on comparing the positions of each common substring in both sequences. Getting the distance between the two positions, n = S1.x1 - S1.x2 then inserting number n of “=” in front of the substring with the little position in the hosting sequence until the two positions become equal. This action leads to increasing the position value of each subsequent substring in the short list. Fig.7 shows the two aligned sequences and the updated positions in the short list.

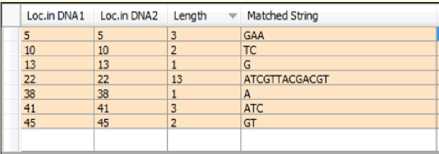
Fig.7. The Preliminary Aligning of the two Sequences

List.4: Alignment algorithm

// input : short list of the common substring

• S1 .filler =””;

• S2 .filler =””;

foreach substring in the short list

{ temp = "";

x1 = position of the substring in the major sequence ;

y1 = position of the substring in the minor sequence ;

• x = x1 + S1.filler;

• y = x1 + S2.filler;

if (x < y)

{

• S1.filler += y - x;

for (int i = 0; i < y - x; i++) temp = temp + "=";

} else if (y < x)

{

As shown in Fig.7 there is an exception case where the two characters “T” and “G” are unaligned. This case occurs when the sum of substring’s position value plus the length of this substring is less than the position of the next substring in the same sequence. To overcome this situation, another procedure should be performed to detect the similar cases inserting number of “=” in the proper positions in both sequences (see Figure 8)

Fig.8. The two Sequences After Complete Aligning

• III.    Implementation

The suggested system consists of two main algorithms, the matching algorithm and aligning algorithm respectively. The first one handles the process of finding the common substrings between two DNA sequences. It generates a list of common substrings along with their lengths and locations in both DNA sequences. The second algorithms processes the generated information from the first one yielding two new DNA sequences where all possible homologous substrings are aligned together (Fig.9). The system has been designed and implemented using C# language.

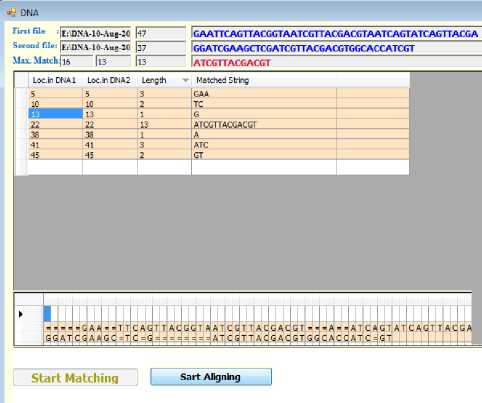
Fig.9. Snapshot of the Program

• IV.    Conclusion

The algorithm proposed in this paper addresses the problem of locating the longest homologous substrings in two different sequences and consequently generates two new aligned DNA sequences. It is based on the convolution between the two DNA sequences (named major sequence X and minor one Y ) and creating a node for each matched substring between the two sequences. If two or more matches share the same location in string X , the corresponding nodes will construct a single linked-list yielding a group of linked-lists containing nodes arranged in certain manner representing all possible matches between sequences X and Y . A list of the common substrings are then constructed, sorted and got rid of repeated ones. The short list of the common substrings are then more processed yielding the aligned sequences with the priority given to the longest common substring. The prposed algorithm could be more developed to locate and align the longest common strings between the major DNA sequence and several minor sequences. Moreover, the algorithm needs to be developed to be able to run in parallel processing manner to cope with the long time processing problem.