A New Hybrid Encryption Approach for Secure Communication: GenComPass

Electronic communication devices such as phone, tablet, computer that we use in our daily life have a big share in communication. The most important parameter in communication through such technological devices is security. It is very important for the communication security that the sender's message reaches the receiver correctly and safely. Information security studies on this issue have been increasing recently [1,2,3]. In the concept of information security, it is important to protect information and restore data integrity when necessary [4]. Cryptology science is used to carry out these operations. Cryptology enables the text of the character set to be transformed into a different form that cannot be understood from its current form by using certain techniques [5,6]. The process of sending the transformed character set safely to the other side is also included in the field of cryptology science [7].

We can divide the encryption algorithms used today into two. These are symmetrical and asymmetrical according to the encryption formats. In symmetric algorithms, the encrypting key and the decoding key are the same [6]. For this reason, it is important to hide the key. Data Encryption Standard (DES-Data Encryption Standard) and advanced encryption standard (AES-Advanced Encryption Standard) are examples of symmetric algorithm. The security of the DES algorithm is due to the difficulty of decrypting without the key length and the knowledge of the key. DES is a Feistel password with a key length of 56 bits. Encryption and decryption processes are open to all humanity [8]. The AES algorithm is a symmetric key cipher that both the sender and the recipient use a single key for encryption and decryption [9]. The data block length of the AES algorithm is fixed at 128 bits [10]. In asymmetric algorithms, two keys are used for encryption and decryption, open and private. The person receiving the public key generates the secret key to be used for the solution [11,7]. It does not make sense to take the public key alone by third parties. RSA (Rivest-Shamir-Adleman) crypto system can be given as an example to this algorithm [11].

The fact that selecting keys for public key encryption is a selection process in which various keys can be categorized according to their suitability, making heuristic algorithms a good option for the process to be followed to generate keys. The power of the key produced using the Heuristic Algorithm is based on the random structure, making it as successful as other switching methods. The complexity of these algorithms is also lower than other statistical methods [12]. Many intuitive methods developed for key production methods are used [13,14,15].

The difference of this study from similar studies is the length and random value of the key that will be used for encryption before encryption. While key lengths used in similar studies vary between 32 -128 bytes, in this study, keys up to 256 bytes can be produced. Genetic Algorithm and Particle Swarm Optimization algorithm, which is an intuitive algorithm, is used as a hybrid for key generation. The Shannon Entropy Algorithm was applied as the Compatibility function of the keys produced. Randomness measurements were provided using the function of this method. The randomness values of the keys used in similar studies obtained 95% results from the Shannon Entropy Algorithm [13] while the keys produced in this study reached up to 99%. The keys produced by heuristic algorithms are compared in terms of parameters such as production time, encryption times, resolution times, key spaces.

When the studies in the literature are analyzed, the new algorithms are compared with the existing algorithms, compared to the switching spaces and their temporal performance [20,21,22]. In this study, a comparison was made in terms of both situations.

In the second part of the study, encryption algorithms and their uses in the literature; In the third section, the details of the data encryption algorithms developed, the application developed and the interface designed, the discussion of the data obtained in the study conducted in the fourth section, finally the results and suggestions of the study in the fifth section are clearly revealed .

Our goal in this study is to implement encryption-decryption using smart optimization techniques for secure communication. Our expectations from the application are expected that the encryption and decryption speeds will be acceptable compared to the existing algorithms and the security space will be stronger than the existing algorithms.

2.    Related Work

Nazer and coworkers performed a study with genetic algorithm method to increase password security. By dividing the key to be used for encryption into bits, it has undergone crossing. Then, for the mutation process, he converted 1 of the bits to 0 and 0 to 1, and obtained a key of 80- 128 bits. He compared the results he obtained with DES and AES encryption algorithms in terms of encryption time, key space and decoding times in the attack. Although unsuccessful results were obtained according to DES as the encryption period, more successful results were obtained in terms of the time to be resolved in case of attack [13]. The key length range produced for encryption in this study is between 32 and 2048 bits. This feature will increase key security.

Kösemen and his colleagues conducted a study on the so-called random number generator based on genetic programming for the wireless recognition and detection platform. A 16-bit number selected from the random number generator should not be predictable with a better probability than 0.025%. This requirement was checked by serial correlation calculation of the array produced using the ENT Test Package. 128 MB files created with a random number generator have been tested and all results have passed the test successfully [14].

Sindhuja and Pramela conducted a study on symmetric key encryption technique using Genetic Algorithm. A numerical value table was created for 25 letters. When the text is entered, each character is converted into a bit equivalent in its value in the table. It was later suggested that a symmetric key was produced by passing through the crossing and mutation steps [15].

Ivanov and coworkers have studied reverse genetic algorithms to produce bifective s-boxes with good cryptographic features. It is often used for symmetric encryption. The purpose of its use is to place the information to be encrypted into a binary form, after which it is placed in the box in the matrix logic and to determine who will be replaced by a table. In this study, a reverse genetic algorithm is proposed. By using the algorithm, a large number of powerful bi-directional S-boxes of any size have been created from (8 × 8) to (16 × 16), which have sub-optimal properties close to those of the S-boxes [16]. The reverse genetic algorithm proposed in this study can process 64 and 256 bits on s-boxes. In this study, a reverse algorithm can be run at the desired value between 32-2048 bits.

Khan and coworkers propose a new technique on encryption using Genetic Algorithm. In the first step, a binary population was produced. Each cell is produced using the so-called random number generator of the programming language. If the so-called random number generator creates a number greater than 50, the generated number is 0. Otherwise it is 1. Each chromosome contains 25 such cells and the number of chromosomes in the experiment is taken as 1000. Examples, gap test, frequency test, etc. meets most of the tests, including. Thus, the belief that the algorithm is strong is strengthened [17]. The number of iterations to be carried out in this study is taken from the user. In this study, it is said that a powerful algorithm has been obtained for 1000 chromosome value with 25 cells. In this study, there is an algorithm that performs up to 10000 chromosomes with 2048 cells. It can be said that the algorithm applied in this study is more powerful.

Delman conducted a thesis study to compare the performance of traditional cryptanalysis methods with genetic algorithm (GA) based methods and to determine the validity of typical GA based methods in cryptanalysis. In the study, 7 of 12 Genetic Algorithm attacks in the literature were retried and 3 of them were successful. As a result of the study, it was concluded that traditional cryptanalysis methods are more successful and easier to implement [18]. Bhattacharya and coworkers conducted a study on Steganography using Genetic Algorithm. Steganography is the art of hiding information. In this study, they worked on image encryption. They used an 8-bit key for encryption. The image is distorted in two steps. In the first step, they were subjected to XOR processing with the key produced with 8 bits and reached new bits. The encrypted output file is once again corrupted by a good Transposition operator produced by applying GA. Finally, the distorted image is embedded within the host image. As a result of the study, a successful encryption process was performed [19]. In image encryption, the image is converted to black and white colors, meaning 1 and 0. The bit length used in switching does not matter for image encryption or data encryption. In this study, the key length can be adjusted between 32-2048 bits. It supports the preferred key length for successful encryption in this study.

Meneses et al. Developed a meta-intuitive model using the Particle Swarm Optimization technique to solve the nuclear reactor loading problem for the pressurized water reactor. In the PSO technique, 50,000 improvements were made for 100 turns of 423.74 particles [20]. Zahran and Kanaan have implemented feature selection application using Particle Swarm Optimization technique. It was concluded from the results that PSO has a strong discovery ability [21]. Uddin and Youssef have worked on simple key encryption using Particle Swarm Optimization. In the study, the main disadvantage of the PSO technique was shown as its great sensitivity to parameter changes such as c1 and c2 [22]. In the studies carried out with the particle swarm optimization technique, a certain number of laps was determined and the path was continued with the improvements and values obtained after the number of laps. In the application carried out in this study, with the Particle Swarm Optimization, the key entropy value, not the number of laps, was requested from the user and the tour was continued until it reached the target value.

When the literature is examined, Genetic Algorithm and Particle Swarm Optimization techniques have been used to create keys in generating cryptological data. In this study, the algorithm that generates the best key was chosen by comparing the parameters of two separate algorithms. The selected key is presented to the user to encrypt the message.

3.    Improved Application: Gencompass

In the study, hybrid method was used to create the key of the message to be sent to the recipient. The algorithms that make up the hybrid are Genetic algorithm (GA) and particle swarm optimization (PSO). Shannon compliance function is used to clarify the complexity of the key to be created. With the method (GA and PSO) that obtained a more successful result in the compliance function, the key was created, and the message was encrypted and sent to the other party. The message sent was resolved by running the reverse algorithm on the opposite side. After this point, how the two methods used are applied to the study. Using these two methods, 2 different keys were produced and the most successful key from the compliance function was used for encryption. In the last step, the application called GenComPass developed in this study shows how the encryption process is performed on the interfaces.

• 3.1.    Genetic Algorithm Method

  The basic principles of genetic algorithms were first introduced by John Holland at the University of Michigan. Holland combined his work in 1975 in his book, Adaptation in Natural and Artificial Systems. First, Holland used the laws of evolution for optimization problems within genetic algorithms [23].

In order to create a key with the Genetic Algorithm method, a value consisting of random or zeroes in a length determined by the user is used first. The bytes formed are cross-processed with 3 different algorithms. Single point crossing, which is the first of three different algorithms used in crossing, is shown in Fig.1 The second crossing from two points is shown in Fig.2 Third, the multi-point cross is shown in Fig.3.

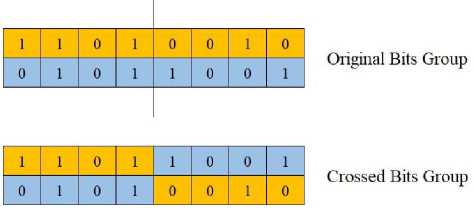
Fig.1. One-point crossover

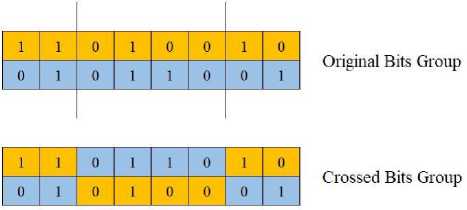
Fig.2. Two-points crossover

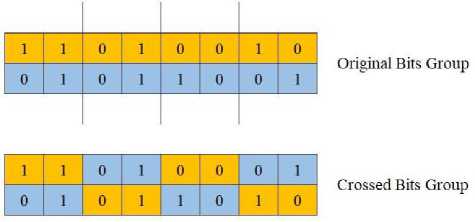
Fig.3. Multi-point crossover

Different crossing techniques are shown in Fig.1, Fig.2 and Fig.3. New bit groups obtained by crossing the current bit groups by separating them from one point, two points and multiple points are shown. Multipoint crossing has been shown to complicate the set of bits at hand.

Then, each byte was spot mutated from a randomly selected bit. In order to obtain more powerful keys as a requirement of the Genetic Algorithm, the mutant key we have created with the existing key we have, has been subjected to the compatibility function. To measure the randomness of the generated key, the conformity function based on the Shannon Entropy Algorithm was used. The mathematical model of the Shannon Entropy Algorithm is shown in Formula 1.

n

H = - £ P i log 2 P                                      (1)

i =0

H: Each n-bit Entropy value,

Pi: Frequency of a certain character in binary sequence.

By comparing the results, the key with high value was selected and the tour was continued. In the process of creating keys with Genetic Algorithm, the results obtained from the Compliance function are terminated at the end of the tour determined by the user or when the Entropy value determined by the user is reached.

Key Production Algorithm Steps:

• 1-    A key between 32 and 256 bytes selected by the user is created.

• 2-    A random value is kept for the selection of the crossing method. Crosswise operation is performed according to the value kept.

• 3-    For the mutation process, the bit to be changed randomly is determined. Mutation process is performed according to the determined value.

• 4-    Subsequently, the mutant key is divided into groups of 8 and the key particles for each group are subjected to the compliance function.

• 5-    Results returned from the compliance function for each byte are obtained.

• 6-    If the suitability value of the mutant key is greater than the suitability value of the previous key, the mutant key value is assigned to the new key value.

• 7-    If the tour value reaches the value determined by the user, the optimization process is terminated.

• 8-    All data of the process is printed on the file.

• 3.2.    Particle Swarm Optimization Method

  Particle Swarm Optimization is inspired by the observation that the movements that some animals moving in swarm meet their basic needs such as finding food, affect the other individuals in the swarm and reach the purpose of the swarm more easily. Kennedy and Dr. It is an optimization algorithm developed by Eberhart in 1995 [24].

The interface created to generate keys with genetic algorithm is shown in Fig.4. In the created interface, the user can determine the key length in the range from 32 to 256 Bytes. The key to be produced can determine the entropy value they want to have in the range of 0.00001 to 1. In order to reach the determined entropy value, the number of iterations can be determined up to a maximum of 10000.

The key that will be generated first in GenComPass can be composed of random bits according to the user's request, Copyright © 2020 MECS                            I.J. Computer Network and Information Security , 2020, 4, 1-10

or it can consist of 0's that are set as the default value of the software. The key bits generated when the key generation process is started are shown in series. All of the generated key is bit mapped and the bit distribution is made to be understandable. When the key generation process is completed, the number of iterations until the desired entropy value, key generation time and entropy value are shown in the interface shown in Fig.4.

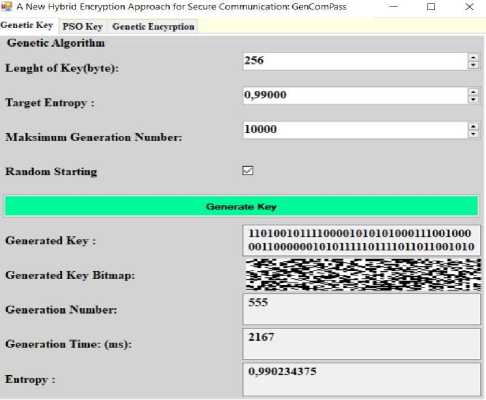
Fig.4. Key generation interface with Genetic Algorithm

Particle swarm optimization, one of the clever optimization methods, was used to create the key. In the applied method, a lot has been created with the number of elements in the value determined by the user. Each element of the particle swarm created is given a numbering label to keep track of their progress. To create the key, a byte-length key determined by enough users for the whole swarm was created. Formula 2 was then used to optimize each element of the swarm created.

v = V ⁺ c l x rand i x ^{( P} best — ^X ) ⁺ c 2 x rand 2 x ⁽ g best — ^X )

• X: particle value,

• V: speed of change of the particle,

• C1, c2: fixed values,

Rand1, rand2: randomly generated values,

Pbest: the situation where the particle is most close to dissolution,

Gbest: the most approached solution to all particles

The speed of our swarm (V) is set as the number of bytes to be changed on the key. Repeated bytes were searched to determine which bytes to replace on the key. The Compatibility function based on the Shannon Entropy Algorithm was used to measure the randomness of the generated key.

For the correct optimization of the swarm, random bit change was applied on this part by finding the first detected of the repeating parts from the parts of predetermined length. Afterwards, the new speed of the final particle was calculated and the next round was started. The optimization process continued until the swarm optimization value reached between zero and one determined by the user, or until the maximum number of laps determined by the user.

Key Production Algorithm Steps:

• 1-    For each individual of the swarm, a key between 32 and 256 bytes selected by the user is created.

• 2-  If repeated peer bytes are encountered, a random bit of the first byte that is similar is changed.

• 3-  After the key created, the key particles are subjected to the Compliance Function for each byte.

• 4-    If the suitability value is greater than Pbest value, the value is transferred to Pbest. The key is best passed to the private key widget variable.

• 5-    If the suitability value is greater than Gbest value, the value is transferred to Gbest. The key is best transferred to the universal key variable.

• 6-    In the next step, how many bits are changed on the key is calculated to increase the optimization value.

• 7-    If the Gbest value reaches the value determined by the user or if the number of laps determined by the user is completed, the optimization process is terminated.

• 8-    All data of the process is printed on the file.

The interface created to generate keys with Particle Swarm Optimization is shown in Fig.5. Unlike Genetic

Algorithm, swarm count parameter is added.

PSO Key Genetic Enryrption

Par^acik Siirii Algoritmasi

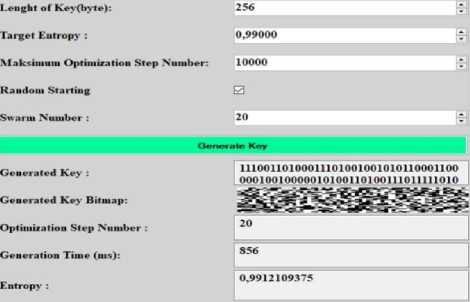
Fig.5. Key generation interface with Particle Swarm Optimization

• 3.3.    Implementıng Encryptıon wıth Gencompass

Of the two methods used to start the encryption process, the most successful key was chosen in the previous step. The encryption steps of the message to be sent over the most successful key are performed in the order given below.

• •    The key is generated with the genetic algorithm technique

• •    Key is produced by particle swarm optimization technique.

• •    The high randomness value is selected from the generated keys and transferred to the encryption interface in binary form.

• •    The message to be encrypted is received from the user.

• •    The message to be encrypted is converted to binary form according to ISO- 8859-character set of ASCII value.

• •    With the key entered, the message is encrypted by subjecting the genetic algorithm to the processing steps.

• 3.4.    Decryptıon of Encrypted Message

The interface showing the implementation of the given steps to encrypt the message is given in Fig.6.

4 A New Hybrid Encryption Approach for Secure Communication: GenComPass —     □

Genetic Key PSO Key Genetic Encyrption
Sending Message Key KeyfBits) Sending Message® Cross Bit Mutant Bit Message	You hare a secret messages. 17:00. Isparta
	011011101001001111011101110110001010011000011101101000100011001101100111011100000000 шплп/^п rmn aiai лл1 Mln лппшпш лиги ми ли ллчллп ллл1 ллл1 МЛ1 ni Л1 ллп Л1 лли л
	110Ш10 11111010 00011011 00111010 00111100 00101001 10011011 10101011
	01011001 01101111 01110101 00100000 01101000 01100001 01110110 01100101 ЛП1ППОПЛ А11ЛППЛ1 АЛ1АПААА АТ11ПЛ11 П11ЛЛ1П1 АН ЛАПП АН1АЛ1П А1ТЛЛ1Л1
	01011111 01101001 01100001 00110100 01100001 01101000 01100110 01110101 АЛ1ЛЛЛА1 Al 1ЛЛАЛЛ ЛЛ11ЛЛ11 АН ЛЛАЛЛ АПЛАТН А1ТЛЛАЛ1 АП1П1А1 Л1ТЛЛЛ1Л
	01011101 01101011 01000001 00010100 01110001 01111000 01000110 01010101 АЛ1Л1АА1 А11Л1АЛА АП1ЛЛ11 ПЛ1ААЛАЛ А111П111 П1Т1ПЛЛ1 ПППЛ1П1 лттимпп
	]kAQqKFU}h5 wqer я OaiqqS^DuctjcQ'jrx Bxrqs па
	Encrypt Outgoing Message

Fig.6. Outgoing message encryption interface

The design seen in Fig.7 has been created so that the incoming message can be decoded correctly. In order for the message to be resolved correctly, the key used when encrypting must be entered correctly. The algorithm used to encrypt the message during the solution phases was reversed. The following steps are followed in order to resolve the incoming message.

• •    The encrypted message is converted into a binary form.

• •    Mutant bits are detected.

• •    The crossover process used in encryption is reversed.

• •    The expression in binary form is converted to characters.

« A New Hybrid Encryption Approach for Secure Communication: GenComPass

Genetic Key PSOKey Genetic Ency rption du have a secret messages. 17:00. Isparta

110Ш10 11111010 00011011 00111010 00111100 00101001 10011011 10101011

01011001 01101111 01110101 00100000 01101000 01100001 01110110 01100101

01101001 01100001 00110100 01100001 01101000 01100110 01110101

Encrypt Outgoing Message

01011101 01101011 01000001 00010100 01110001 01111000 01000110 01010101

11011110111110100001101100111010001111000010100 iioouonioioiouoiioioioiooiooooiiio

11011110 11111010 00011011 00111010 00111100 00101001 10011011

01011101 01101011 01000001 00010100 01110001 01111000 01000110 01010101

01011111 01101001 01100001 00110100 0U0OOO1 01101000 01100110 01110101

01011001 01101111 01110101 00100000 01101000 01100001 01110110 01100101

You have a secret messages. 17:00. Isparta

• Fig.7.    Incoming encrypted message decoding interface

When the correct key is not used for the solution of the incoming encrypted message, the message will remain data protected since it will never be converted correctly. An example of the message to be solved with an incorrect key is shown in Fig.8.

« A New Hybrid Encryption Approach for Secure Communication: GenComPass

Genetic Key PSOKey Genetic Encyrption

Sending

Message

Key

Key(Bits)

Sending MessagefBi

Cross Bit

Mutant Bit

Cryptic

Encrypted message

Key (Bits)

Mutant Bit

Cross Bit

Incoming

MessageBit

Incoming

Message

You have a secret messages. 17:00. Isparta

QUO 111 0100100111101110 UI0110001010011000011101101000100011001101100111011100000000

11011110 1Ш1010 00011011 00111010 00111100 00101001 100U011 10101011

010UO01 01101111 01110101 00100000 01101 000 01100001 01110110 01100101

01011111 01101001 01100001 00110100 01100001 01101000 01100110 01110101

01011101 01101011 01000001 00010100 01110001 0U110O0 01000110 01010101

Encrypt Outgoing Message

11010O101O0101100101111111O111011O101101O00111O010U0110111OO0O0O010O011011010111100

11010010 10010110 010U1U 11011101 10101101 00011100 10110110 11100000

М»ЛПЛ11 niln,nil nnCwVAnn innwiic nimWiin ппгиплп nlaruwivr hliitncinr

010П101 01101011 01000001 00010100 01110001 0U110O0 01000110 01010101

01111101 01001011 01000011 ОО010ПО 0Ш00О0 01111001 01000010 01010001

01111011 01001101 01000110 00010011 0Ш0001 01111000 01010001 01000010

Dcyrpl Incoming Message

• Fig.8.    Example of deciphering incoming encrypted message with wrong key

4. Discussion

In the application coded with C#, genetic algorithm and particle swarm optimization, key generation steps, encryption steps, decryption steps, fitness function results are printed on the console screen step by step. In order to measure the times, an object from the StopWatch class has been produced and measured with this object.

The change of the results obtained from Equation 1 in the iteration process of the key created using the genetic algorithm and Particle Swarm Optimization is shown in Table-1.

G best : Best Value in the Swarm

P best : The Best Value of Swarm Staff

H: Fitness Function Value

SSN: Swarm Staff Number

NI: Number of Iterations

Table 1. Change of the fitness function results of the key produced by genetic algorithm and Particle Swarm Optimization according to the number of iterations

Genetic Algorithm		Particle Swarm Optimization
NI	H	NI	SSN	H	G best	P best
1	0,9236	1	1	0,9256	0,9256	0,9256
9	0,9281	35	5	0,9354	0,9566	0,9354
27	0,9299	49	16	0,9422	0,9644	0,9422
59	0,9351	61	5	0,9517	0,9660	0,9517
71	0,9402	69	16	0,9433	0,9701	0,9467
86	0,9419	74	1	0,9585	0,9701	0,9585
280	0,9525	183	5	0,9705	0,9764	0,9705
808	0,9601	191	16	0,9681	0,9764	0,9685
9999	0,9900	224	1	0,9807	0,9807	0,9807

The entropy value change graph obtained from the conformity function results of the keys created during the iteration process is shown in Fig.9.

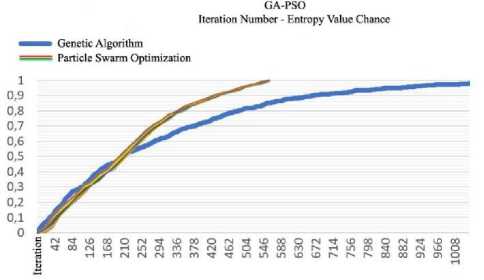
Fig.9. Random values of GA and PSO elements by optimized step count

When we measure the randomly selected start times of the keys we produce with Genetic Algorithm and Particle Swarm Optimization techniques, it is seen in Table-2 that PSO has a faster performance than GA. While GA has an average speed of 1533.4 ml, PSO has an average speed of 679.1.

Table 2. Temporal performance comparison of switches produced with GA and PSO

Encryption Comparison	Genetic Algorithm	Particle Swarm Optimization
Average Key Generation Time (ms) (Random Starting)	1533.4	679,1

The key spaces of encryption with GenComPass and AES are compared. GenComPass can generate 256 bytes long keys, while AES can create 32 bytes long keys. Therefore, the switching space of GenComPass created in the study is 21792 times of AES. In this case, the attack response time of the keys produced with GenComPass is high. For example, as seen in Table 3, it is seen that GenComPass will be much stronger than the AES algorithm due to key lengths, when brute force attack with 1000 key generation power per second is applied and resolved.

Table 3. Security comparison of passwords produced with GenComPass and AES

Encryption Comparison	GenComPass	AES
Maximum Switching Space	2048	2256
Decryption Time (1000 Key/ms)	0,99 x 2 2148	0,75 x 2 256

In order to encrypt with the AES algorithm, we have created an object from the AesCryptoServiceProvider class in our application, which we have encoded in C #, and performed its encryption through this object. In order to measure the encryption time, we produced an object from the Stopwatch class and measured the moment between the start and end of the encryption process. When it encrypts 300 characters of text with GenComPass and AES and the encrypted message is decoded, the temporal performance measurement values are compared and shown in Table 4. In general, although AES gives successful results from GenComPass, GenComPass can be considered as an alternative algorithm to AES since the performance differences are acceptable.

Table 4. Comparison of the encryption and decryption times of the message with GenComPass and AES

Encryption Comparison (300 characters)	GenComPass	AES
Encryption Time (ms)	4714	4877
Decryption Time (ms)	108011	7304

5. Conclusion

Studies in the field of information security are increasing day by day. One of the important subtitles of information security is secure communication. In this study, the message to be sent by encryption was encrypted with a hybrid key created using both the genetic algorithm method and the particle swarm method, which is one of the smart optimization methods. The encrypted message was transmitted to the other party and resolved by applying reverse algorithms. The encryptions made using the generated key were measured and the results of the AES algorithm were compared. The proposed method has performed more successfully than a current valid algorithm in terms of maximum switching space and encryption time. As a result, this study has revealed an alternative data encryption and decryption method that can be used in mutual communication.