A New Method for Graph Queries Processing without Index Reconstruction on Dynamic Graph Databases

Published Online February 2017 in MECS DOI: 10.5815/ijmecs.2017.02.06

Graph is a general data structure used to model complicated and schema less structures. For instance, utilization of graph can be seen in areas such as food chain, UML diagram, software engineering, social networks [1,2,3], ERD diagrams in database [4], gas, water, electricity, and communication, telephone, technology transportation networks, and XML documents [5,6,7]. Graph database system is a database system used to manage graph data. The action of searching a database for preferred models is known as graph mining [8,9,10,11]. Given the wide range of graph mining applications (e.g. detecting anomalies in network [12], Internet links analysis [13, 14], graph query indexing [8,12,13,14], and medicine [15,16]), great deal of research works have been done on graphs. An interesting matter as to graph mining is graph containment problem. For instance, suppose D = {5i, 52, 9з> —, Sn) be a graph database with тг independent graphs, then query q needs to search all graphs in the database. One of early solutions to do this is to test the whole database with regard to isomorphism, which is not effective as with increase the number of graphs, demand for memory and response time increase exponentially. To deal with this, new methods tried to conduct the query in two steps.

• 1.    Index Construction : the database is scanned and a set of features needed to determine and prune a portion of the database where the answer of query probably is not there is determined. The closer the set of the candidates to the final answer, the higher the performance of the query. This step is offline to be ready to response.

• 2.    Candidate Verification: the candidate graphs obtained in the previous stage are tested as to isomorphism and if the graph is contain the query add to answer set. The paper is arranged as follows: firstly related works are described also definition of the terms and concepts of graph mining (which is not recommend for experienced readers). Section three represents architecture of the proposed method in more detail. Section four discusses the results obtained by the proposed method. The last section concludes the article with conclusion and suggestions for future works.

• II.    Related Works

There have been in [17] paths were used to constructed the index however, demand for memory was not optimum with increase of index volume and the best performance of the proposed method was obtained with small databases. Frequent subtrees [18] were used in [19] to constructed the index and consequently, considerable increase in tree mining was obtained. Still, the proposed method had the disadvantage of failing to prune the search space as the tree structure is simpler than graph. Frequent subgraphs were used in [20] and closed frequent subgraphs [21] were used in [4] to construct the index. Their results show that considerable decrease in query time was obtained when the query was indexed. On the other hand, accurate query processing method failed to function properly with large databases, which led to introduction of similar graph queries [8]. The one challenge faced with by all these methods is that the index must be reconstructed when the database is updated and index construction is time consuming. The proposed method in this paper suits both static and dynamic databases. The main idea is to use Positional Inverted Index (P.I.I) used by search engines. The proposed method relies on hashing technique to implement and store required features, which gives the inverted index opportunity to be updated. In addition, the index can be updated as fast as possible when the graph database is changing, which avoids necessity of totally index reconstruction. Regarding query processing is parallelizable, multithread and vertex invariant techniques are employed to improve checking the candidates [22]. These techniques improve speed of isomorphism test on the subgraphs.

Definition 1. Dynamic graph : A graph in which the edges are added or removed over time so that its structure changes permanently.

Definition 2. Transactional graph database: The data are represented as a set of several independent graphs (e.g. protein, amino acids, and chemical/biological informatics databases). Fig. 1 . illustrates a graph database comprised of 4 graphs.

Definition 3. Query processing: Assume D = {5 , , 5₂, —, 5 n } as a graph database includes N graphs, then a graph query processing is defined: a graph query q is given, all д i E D, where д , is a subgraph of q, are returned as a member of answer set. Fig 1. illustrates a graph database and Fig 1d. represents a graph query that returns {a, b} as the answer set.

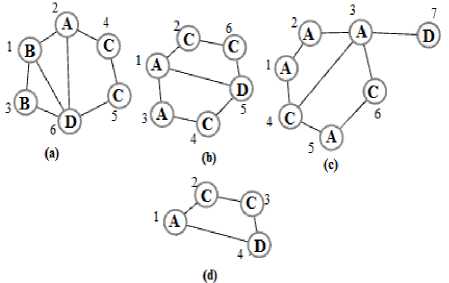
Fig.1. Graph database including 3 graphs (a,b,c) and (d) a graph query

• III.    Proposed Method

The proposed method for graph query processing is comprised of two parts:

• A.    Index construction

• B.    Query processing

The index is used to prune part of the search space that does not contain the query answer. To construct the index, the graph database is scanned and, then, a set of features of the database is extracted and stored. The main idea have to use the well-known positional inverted index used in search engines (Fig 2). In short, 1,, 2,,t,,—,tn are the key terms obtained from the graph database. To accelerate obtaining the key terms, hashing technique was used. Each node in the positing list, implemented using linked list, is comprised of two parts: 1. d,оc — ID that represents graph number (No), and 2. Position that represents frequency of each edge and other features of the graph. Two hashing tables were used here to improve access to the features, one to store the edges and another to store neighborhood of each node. In addition, columnbased technique (when key/value technique in a hashing table is not the answer to the problem, value section can be implemented as key/value) was used to implement the tables and multithread and thread pooling techniques were used to improve query processing. Following parts discuss each step of index construction and query processing in detail.

A. Index Construction

The index construction is capable of being updated in case of change in the graphs of the database. Two hashing tables, implemented using column-based techniques, are used to construct the index. So that, one table constructs an inverted index on the edges and another constructed as inverted index on each node and the neighbors. figure 3 illustrates general architecture of the index. Detailed explanations of each section are brought in what follows.

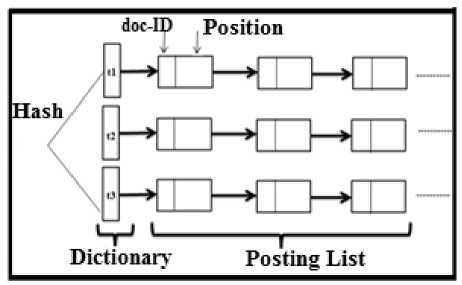
Fig.2. Positional Inverted Index (P.I.I) structure in search engines

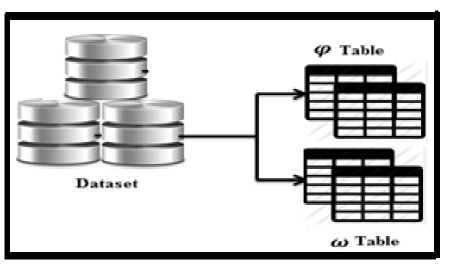
Fig.3. Index construction architecture

A.1 Construction of Table p

The table is used to store the edges and graph number. The table indicates number of each edge in each graph and number edges of each graph. Fig 4. illustrates a transactional graph database with 2 graphs and table p is filled out like Table 1. according to Fig 4. According to Table 1, edge AB in graph No1 extends between vertex No.1 and 3 and between vertexes 1 and 4 in graph No 2. In addition, it is clear that edge AC occurs two times in graph No.2 between vertexes 1 – 3 and 2 – 3.

Table 1. Table p

Key(Edges)	Key(graph id)	Values(labels)
AA	1	1,2
	2	1,2
AB	1	1,3
	2	1,4
AC	1	1,4
	2	1,3#2,3
BC	2	3,4
CD	2	3,5
AD	2	1,5

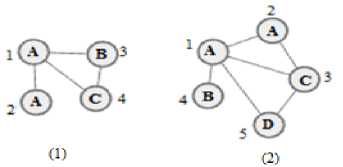
Fig.4. A transactional graph database with two graphs

A.2 Construction of Table to

The table is used to store each node along with its neighbors. An advantage of the table is that it can determine the number of nodes of a graph, frequency of each node in a graph, and number of neighbors of each node. Table 2 indicates how a table и is filled out based on database of Fig 4.

Table 2. Table co

Key (graph ids)	Key (nodes)	Value(Neighbors)
1	‘A’	‘A’%’A’#’B’#’C’
	‘B’	‘A’#’C’
	‘C’	‘A’#’B’
2	‘A’	‘A’#’B’#’C’#’D’%’A’#’C’
	‘B’	‘A’
	‘C’	‘A’#’A’#’D’
	‘D’	‘A’#’C’

For instance, according to table ω, one may say that graph No.1 has two ‘Л’ nodes so that one has ‘Л’ as its neighbor and another has ‘Л’, ‘ В ’, and ‘ C’ as its neighbors

(# is separator of the neighbors of each node). In the case of dynamic graphs, a thread is used to update the tables and a trigger is used to update the database. Algorithm 1 illustrates how the index is constructed.

Algorithms 1            BuildIndex() Input : Graph Dataset D
Output :	a and P tables
1 . for each graph gt in D
2.	for each edge e j in gt
3.	if (a contains (e j ) )
4.	if( a.get(e j ) . contains(i) )
5.	add label of e j into a
6.	else
7 .	add i and label of e j into a
8 .	else
9 .	add e,- , i and label of e,- into a
10. start j = get start point of e j
11. end j	= get end point of e j
12 . if (P contains ( i ) )
13.	if (P .get( i ).contain(start j ))
14.	add end j to neighbors of start j
15 .	else
16 .	add start j to p and end j as neighbor of
start j
17 . else
18.	add i to p , start j and end j as neighbor’s
start j

B. Query Processing

The constructed index is used to prune the search space and improve performance of query processing. General architecture of the query processing is illustrated in Fig 5.

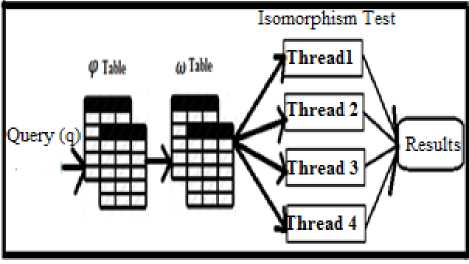
Fig.5. General architecture of query processing

Immediately after placing a query request at the input, frequency of each edge in the query is computed. Afterward, frequency of query edges in the graph database is computed based on the data of Table φ and in turn graph-id is obtained. Afterward, the set of the graphs in which the query can be performed is obtained for each element of the obtained set based on table и and comparing the nodes of a graph (neighbor of the nodes and their labels) and the query. Finally, isomorphism test is carried out on the set of the graphs. Here, multi-threat technique is used so that candidate id-graph set is distributed over threads implemented independently (thread pooling technique) and the threads perform isomorphism test using vertex invariant technique [25]. In general, two threads that are implemented independently are used, one for updating the index (Tables ω and Table φ) and one for collecting queries from inputs and processing. Processing time is obtained as equation.(1).

=           +|   |*|            |

Where, T is the query time between tables ω and φ, |C | is number of candidate graphs that need isomorphism test, and T is the required time of isomorphism test. Query processing algorithm is illustrated in Algorithm 2. In Fig 6 a general architecture of dynamic graph query processing is indicated, when graph database is changed or update (graphs/edges is removed or inserted) a trigger updates the index. Update the index and query processing performed simultaneously.

Algorithm 2      Query Processing()

Input : query q and, , /? table

Output : set of graphs contains q

• 1.    for each edge e , in q

• 2.        send e , into a table and store set of candidate

• 3.    calculate intersection of candidate[i] and put it in SetCandidate1

• 4.    set Temp=SetCandidate1

• 5.    for each ID , in SetCandidate1

• 6.    for each node in q

• 7     calculate frequency of each nodes

• 8.         if (number of node n , in graph[ID , ] less than or

• 9.           if (node n , has neighbors that q has same

• 10.             no actions

• 11.           else

• 12.            remove ID , from Temp

• 13.        else

• 14.        remove ID , form Temp

• 15.    for each ID j in Temp

• 16.       if (graph[ID y ] contains q)

• 17.                 add ID j into Results

IDs in candidate[i]

equal to number of nodes n , in q)

neighbor )

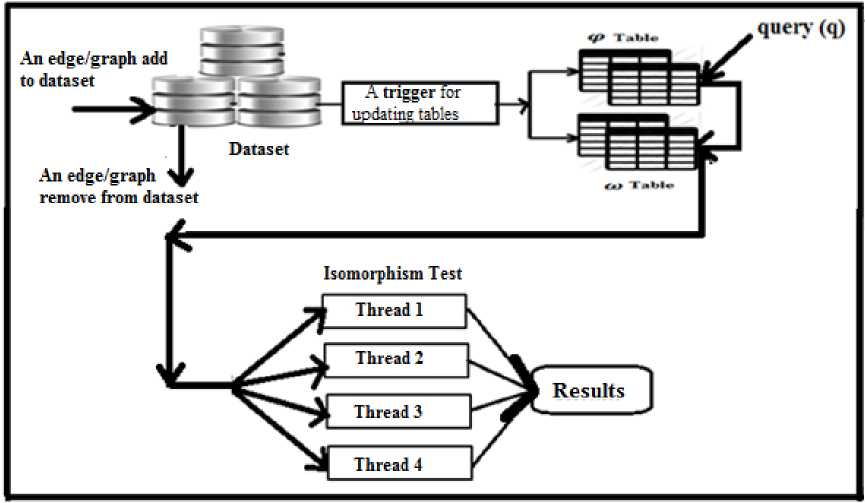
Fig.6. dynamic graph query processing architecture

• IV.    Experiments and Evaluation

The proposed method is implemented in Java, Netbeans IDE6.9, Microsoft Windows 7. The datasets were generated by an algorithm for generating real databases. Fig 7. and Fig 8. illustrate features of the databases. Fig 7. shows the nodes and their frequency and Fig. 8 illustrates the edges and their frequency in different datasets. The datasets features are listed in Tables 3, 4.

In this paper graph queries processing (graph query as a subgraph) was performed on a transactional graph database .That is because the database is used in different areas; for instance, in the case of “malware detection” [23,24,25] several malware are taken as input. By extracting the APIs from the codes (the malware are run in sandbox or VM (Virtual Machine) environment to avoid damages to the system) after retrieval, the APIs of the malware’s codes as “control flow graph” is extracted. Then, according to graph mining algorithms such as gspan [18] frequent subgraphs are mined and indexed [4,19,14]. The obtained index is used to detect the malware (as a signature) .The point here is that, however, when a new malware is introduced, the index needs to be thoroughly updated as the mining algorithm of subgraphs needs to repeat the mining of the frequent subgraphs. This is a serious disadvantage taking into account the rate of generation of malwares. This explains the reason for proposing the method. because the proposed method relies on hashing technique to construct the index, GraphGrep [17] hashing-based technique was selected for comparison. GraphGrep method extracts and stores all the possible paths up to a specific length. Thereby, finding all paths needs considerable time and memory for large transaction graph databases. In addition ,when an edge of the graph is removed (e.g. a malware modifies its structure), the previously stored paths must be updated as well (there are many paths in the index including the removed edge). Moreover, by adding new edge to graph, all the possible paths up to a specific length needs to be extracted and added to the index. This brings high demand for memory need to store the index ,while updating the index is time consuming. Therefore, it was omitted from the assessments as the databases used for assessment were too large and time consuming for GraphGrep to generate index and answer the queries. On the other hand, the proposed method utilizes a proper data structure based on the idea of search engines so that only each edge of the input graph is read for construct the index. In addition, the index can be updated with time complexity of O(1) when new graphs are added or removed from the database. On one hand, GraphGrep method uses the paths to prune the state space and on the other hand the paths, which is the simplest data structure, is not effective in pruning the unwanted graphs, which are not part of the query. It also fails to detect closed loops and rings. Candidate verification stage also needs long time to perform isomorphism test. The proposed method uses invariant vertex technique  [22]  for isomorphism test, which is more effective comparing with previous methods that rely on adjacency matrix for isomorphism test. The reason that the diagrams are pointy at specific values (peak of diagrams) is that degree and label of nodes of the queried graphs are uniform and carrying out isomorph test on the query based increases isomorphism time. However, after distribution, degree and the labels are no longer uniform and thus ,time of isomorphism test is attenuated. Regarding assessments, diagrams are snapshots that are taken at the time of implementation as they are changing permanently. Clearly, the changes on GraphGrep are not displayed as updating the database using GraphGrep is too slow. The point is that GraphGrep is actually designed for static environments and does not suit for dynamic environments.

Table 3. the nodes and their frequencies

Dataset Size
10K		20K	30K	40K	50K
Nodes	#Freq	#Freq	#Freq	#Freq	#Freq
A	12288	24673	37019	49348	61617
G	12166	24491	36726	49089	61407
F	12279	24612	37061	49455	61701
E	12372	24580	36874	49097	61357
D	12288	24329	36661	49071	61513
C	12355	24713	36932	49177	61607
B	12266	24661	36793	48988	61273

Table 4. the edges and their frequency

Dataset Size
10K		20K	30K	40K	50K
Edge	#freq	#freq	#freq	#freq	#freq
EE	3259	6479	9679	12821	16090
BD	6364	12704	19094	25699	32206
BC	6374	12890	19116	25741	32243
BB	3147	6322	9465	12551	15717
CG	6416	12638	19034	25261	31795
CF	6608	13021	19483	26041	32594
FG	6343	12760	19172	25592	32049
FF	3154	6422	9674	13021	16157
CE	6500	12909	19162	25572	31971
CD	6544	12939	19521	26053	32605
CC	3159	6382	9518	12818	16204
AG	6304	12814	19212	25763	32335
AF	6348	12799	19308	25873	32262
DG	6287	12653	19094	25565	32101
GG	3159	6403	9629	12810	16119
AE	6626	12918	19358	25786	32098
DF	6453	12737	19205	25733	32284
AD	6243	12544	19029	25600	32010
DE	6512	12743	19219	25610	32163
AC	6607	13084	19528	25957	32385
DD	3092	6159	9391	12668	15926
AB	6362	12861	19264	25686	32239
AA	3163	6430	9678	12819	16035
BG	6421	12959	19312	25703	32154
BF	6310	12827	19221	25669	32135
EG	6256	12613	19010	25439	31891
EF	6363	12668	19151	25462	31702
BE	6377	12802	19065	25460	31892

Fig 7. illustrated index construction time. clearly, increase of database size leads the increase of time. However, the performance of the index construction shows great improvement thanks to hashing technique.

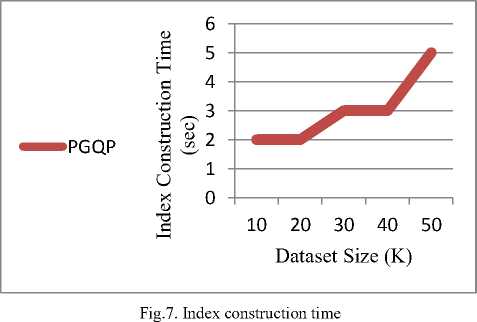
Fig 8, Fig 9, and Fig 10 illustrates query processing them have equal size though with different structure. time. All the queries are selected randomly and some of

PGQP

Query Size

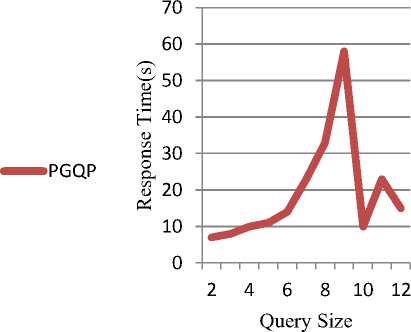
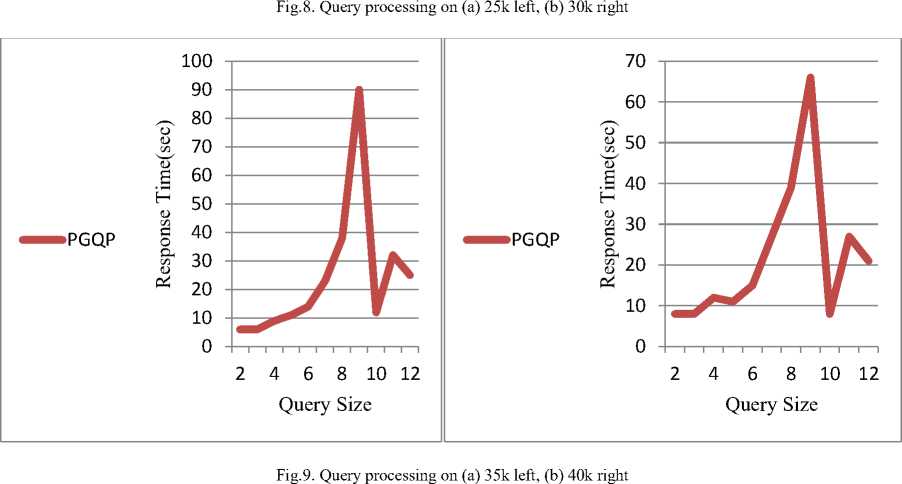
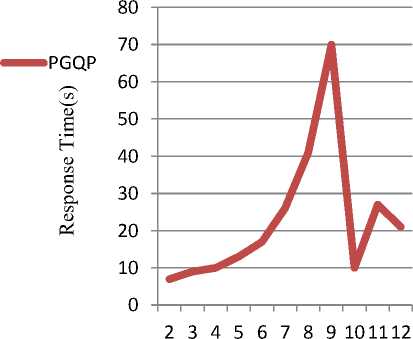
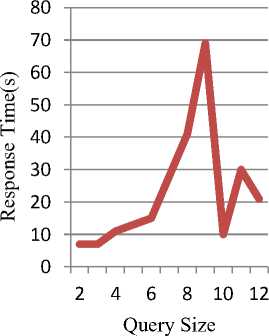
Fig. 10. Query processing on (a) 45k left,( b) 50k right

• V.    Conclusion, Future Works

A short introduction to application of graphs was provided first. Given the weight of graph processing regarding graph mining methods, the pertinent concepts and topics were discussed. An obstacle in the way of graph query processing is that the index of database should be reconstructed each time the graph is changed. To solve this, Positional Inverted Index (P.I.I) used by search engines was proposed. So that the index tables can be updated when the database graphs are dynamic with no need to reconstruct the index. This approach led to considerable increase in query processing performance. Taking into account that graph processing have wide range of applications in different fields, the proposed method can the used for designing online malware detection applications. So that by adding a new virus to the dataset, the signature (i.e. index) does not need reconstruction.