A New method for Image Encryption Using Chaotic Permutation

Published Online April 2020 in MECS DOI: 10.5815/ijigsp.2020.02.05

With the rapid expansion of computer networks and wireless communications, data protection and information security are becoming major challenges to the effective use of information technology. This information is not just text, but all kinds of information such as sound, image, etc. are included. Due to the widespread use of images in human life, the security of images is also vital; for example, it has become important to protect images such as maps of military establishments or map of buildings related to security agencies or diagrams of bank-building constructions. To overcome with this challenge, cryptographic techniques should be used. Cryptography is the science of protecting the privacy and confidentiality of information during communication under unsafe and hostile conditions[1]. Each kind of data has its own characteristics, and so different methods should be used to preserve confidential data from impermissible access. Image applications sometimes need to use data compression for transmission. Traditional encryption methods  require additional activities when transmitting compressed image data, thereby necessitating long computational time and high computing power. Different methods have been proposed for image encryption, each of which has its own advantages and disadvantages. Chaos-based strategies have received widespread attention due to their fundamental characteristics such as stochasticity, dynamic behavior, and sensitivity to initial conditions. The sensitivity of chaotic systems to changing initial conditions and to variations in parameters makes the chaotic trajectory unforeseeable and therefore leading many research studies to implement chaotic algorithms to perform the encryption of images before transmitting them over a media that is insecure and exposed to various types of invasions [4].

Up to now, various image encryption methods have been proposed based on chaos theory. Some of these methods are discussed in the next section. Each of these methods has advantages and disadvantages over other methods. In this article, a novel image encryption technique based on chaos theory and pixel permutation is proposed. Logistic map and Ikeda map are used in this scheme to generate pseudo random bit sequences. A trick has been used in this scheme that makes the encryption process unique for each image. Also, two completely new methods have been proposed for pixel permutation that one of them is based on an ancient Japanese game called

Amidakuji. In this way, some experimental results such as information entropy and correlation coefficient have been improved.

• II.    Previous Works

It is important for any public communication system such as a cellphone network to prevent unauthorized access. Cryptography is one of the most widely-applied methods for maintaining secrecy and the confidentiality of information in public communication networks. The security of image and video information has become increasingly imperative for numerous applications, including video conferencing, medical imaging, and industrial and military imaging systems. Cryptography offers a widely-implemented approach to the security of information and nowadays encryption programs are easily accessible. Encryption algorithms available for textual data are highly effective. Sometimes, however, sensitive information is sent in the form of images. In such cases, we need a highly optimized specialized algorithm to protect this visual information. Images differ from text in many aspects, such as high redundancy and correlation, and the main problem in designing effective image encryption algorithms is the difficulty of shuffling and diffusing image data using classical cryptographic tools. In recent years, many methods and algorithms have been proposed by researchers in this area. For example, in Ref.[11] a cryptosystem used a diffusion layer followed by a bit-permutation layer instead of byte permutation to shuffle image pixel positions. Furthermore, a newly proposed formulation has achieved the permutation layer using a 2D cat map that allows for efficient implementation measured by time complexity in terms of both arithmetic and logic operations and the clock cycles of the key-dependent permutation process in comparison with the standard one. The algorithm proposed in Ref.[12] is based on a complex chaotic Chen system and complex chaotic Lorenz system with greater key space for potential attacks. The researchers in Ref.[13] propose a two-dimensional Logistic-adjusted Sine map (2D-ASM). Performance assessments show that this is more ergodic and unpredictable and has a wider chaotic range than many existing chaotic maps. The authors in Ref.[14] present a novel image encryption algorithm that is based on Bernoulli maps. This algorithm attempts to improve the problems associated with encryption failure, such as a small key space, encryption speed, and low security level. Paper [15] presents a new image encryption algorithm based on a chaotic shuffling-diffusion method. First, a chaotic sequence which is generated by a first logistic map is used to label the row coordinate of pixels of the scrambled image. Second, other logistic map is used to label the column coordinate of pixels of the scrambled image. Then, using proposed new pixel exchange model to change the position of pixels, the effect of scrambling the image is achieved. Third, a matrix that is the same size as the plain image is generated by a third logistic map in order to enlarge the key space according to MOD operation and XOR operation by itself.

In Ref.[16] an algorithm for image encryption based on general two-dimensional Arnold transform with keys and a quantum chaotic map is proposed. First, the key streams are generated as initial conditions and parameters by the two-dimensional logistic map. Second, the Arnold general scrambling algorithm with keys is used to permute the color component pixels R, G and B. Finally, a series of pseudo-random numbers generated by the chaotic quantum map is applied to change the value of diffused pixels. The authors in Ref.[20] proposed an effective bit-level image encryption plan based on a 3D cat map, reverse 3D cat map and an improved class of chaotic maps with Markov properties. In this strategy, firstly, the plain-image is converted into a binary matrix, and then the sum of all the bits in this matrix is used as part of the secret keys; secondly, a mapping is designed; and, thirdly, a chaotic map with Markov properties is used in the diffusion process. In Ref.[21] a new fractional two-dimensional triangle function combination discrete chaotic map (2D-TFCDM) is proposed by utilizing the discrete fractional calculus. Huang and other authors in Ref.[22] presented an image encryption system by using both plaintext-related permutation and diffusion. In this cryptosystem, the parameters values of the cat map used in the permutation phase are related to plain images, and the cat map parameters are also impressed by the diffusion operation.

• III.   Chaotic Maps

  In this paper a new method for image encryption based on chaos theory is presented, so first we will briefly explain this theory. Chaos theory has been established in many different fields of research, such as physics, mathematics, engineering and biology, since the 1970s. Chaos is a branch of mathematics and physics related to systems that are highly sensitive to minor changes in initial values; therefore, their future behavior is not predictable [5]. The key idea of chaos theory is that in all disorder there is order. The most famous characteristics of chaos are the so-called “butterfly effect” (sensitivity to initial conditions) and the pseudo-randomness generated by definite equations. In recent years, cryptographic algorithms based on chaos have proposed new, more efficient ways of developing secure image encryption techniques to meet the demand for real-time image transmission via communication channels. Many unique characteristics of chaotic systems such as sensitive dependence on initial conditions and system parameters, non-periodicity, pseudo-random properties and topological transitivity lead to efficient methods for image encryption[6]. Behavior of chaotic systems shows with mathematical maps. One dimensional and two dimensional maps are usually employed in chaos based image encryption algorithms. One dimensional chaotic maps such as Logistic map, Sine map and skew tent map have advantage of simplicity and easy implementation. In particular, Logistic map was widely used for image encryption. However, it is not secure enough to use only one dimensional chaotic map

because of its small key space and weak security. In this paper, we use two types of chaotic maps in our encryption algorithm: a Logistic map and an Ikeda map. In this section, we briefly review these two chaotic maps.

Logistic signals are some of the simplest and most commonly used signals showing chaotic behavior. Due to its mathematical simplicity, this model remains a valuable test bed for new ideas in chaos theory and the application of chaos in cryptography[7]. It is defined by the following equation:

x , = r . x „ .(1 - x „)                  С¹)

n + 1               n               n

In (1), x_n is the state variable and belongs to interval [0,1] and r is the control parameter and belong to interval [0,4]. Behavior of this map is dependent on r and with respect to the different values of r it present different behavior[8]. If we assume that the initial value(x 0 ) is equal to 0.3 then the behavior of Logistic map is as follow:

If rϵ [0, 3] then the behavior of signal in first ten iteration is somewhat chaotic an after the tenth iteration will be stable. This behavior is shown in fig.1.a.

If rϵ [3, 3.57] then the behavior of signal in first twenty iteration is somewhat chaotic and after twentieth iteration will oscillate between two fixed values. This manner is shown in fig.1.b.

If rϵ [3.57, 4] then the behavior of signal is always chaotic. This chaotic manner is shown in fig.1.c.

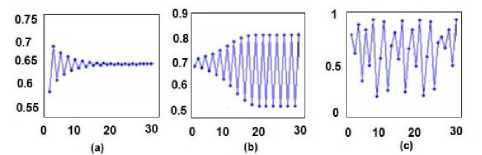
Fig.1. Behavior of Logistic map

Ikeda map is a two dimensional discrete-time map that define by following complex map[9]:

z

= A + B. z

n

i . k .( z 2 + 1) + C

If zn be replaced with its equivalent xn+iyn, then the real section of above equation is as follow:

x„₊, = ^{1 +} u .⁽x n .cos⁽ t n ) - У п .sⁱⁿ⁽ t n ))         (3)

У^, = u .⁽x n .^Sin( t n ) ⁺ y n .c^OS( t n ))         (4)

t = 0.4 - n

1 + x + y nn

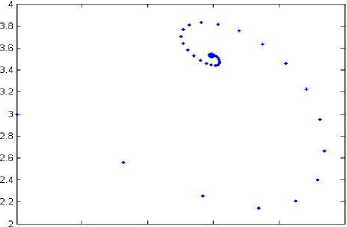
In (3) and (4) u is the control parameter of this map and with respect to the different values of u presents different behavior. If u=0.87 then the behavior of map is completely chaotic. The trajectory of this map with u=0.87 and 10000 iteration is shown in Fig. 2.

2            2.5            3            3.5            4            4.5

Fig.2. Trajectory of Ikeda map with u=0.87 and 10000 iterations.

In this paper a new method for generating pseudo random bits based on chaotic maps is proposed. Two basic chaotic maps that are used in this method were studied in the previous section. First, we show that how we used this maps individually for generating pseudo random bit sequences. Then we present our algorithm that is combination of these two pseudo random bit generators.

• IV.    Chaotic Pseudo Random Sequence Generator

We combine two pseudo random bit generator to make a random sequence generator with good statistical properties. These two methods are discussed in following sections.

• A.    Pseudo random sequence generator based on Logistic map

In Ref.[10], a simple method for generating pseudorandom sequences is proposed. This method is based on two logistic maps that iterated separately starting from independent initial conditions. The pseudo-random bit sequence is obtained by comparing the results of both chaotic logistic maps.

• B.    Novel pseudo random sequence generator based on Ikeda map

In previous section we saw that if the control parameter of Ikeda map be equal to 0.87, this map will be quite chaotic. To generate a pseudo random sequence with length of n bits, first we select x 0 and y 0 between [0, 1]. At each iteration we calculate x i and y i and compute Euclidean distance of them. We called it Z.

Z ( i ) = 7 x ( i )² + y ( i )²                (6)

Now consider the floating part of this number. We separate this part without its point and convert it to binary representation. Now we select its LSB and MSB bits and XOR them. So, one bit of pseudo random bit sequence is produced. With iteration of this process, we can generate a pseudo random bit sequence. In table 1 the steps of this algorithm for x0=0.28 and y0=0.45 and n=8 has been shown.

Table 1. The steps of proposed pseudo random bit generator algorithm for x 0 =0.28 and y 0 =0.45

i	x(i)	y(i)	z(i)	F(i)=float section of z(i)	1 = | i &	b(i)
0	0.2800	0.4500	0.5300	0.5300	1000	1
1	0.5795	0.0543	0.5820	0.5820	1001	0
2	0.6916	0.3488	0.7745	0.7745	1100	1
3	0.4010	-0.1584	0.4311	0.4311	0110	0
4	1.1096	0.3270	1.1568	0.1568	0010	0
5	0.7189	-0.8817	1.1376	0.1376	0010	0
6	0.0906	-0.0359	0.0975	0.0975	0001	1
7	1.0729	0.0276	1.0733	0.0733	0001	1

The generated pseudo random sequence is [10100011].

• C.    Proposed chaotic pseudo random sequence generator based on Logistic and Ikeda map

In previous section we introduced two PRBGs based on Logistic map and Ikeda map. By applying these two PRBGs we propose a novel pseudo random bit generator.

Suppose there is a 2×1 Multi Plexer. Two Logistic sequences are applied to its data inputs, and one Ikeda sequence is applied to its select input. Thus, in each step, one bit of Logistic sequences would be selected by Ikeda Z. This algorithm is shown in Fig.3.

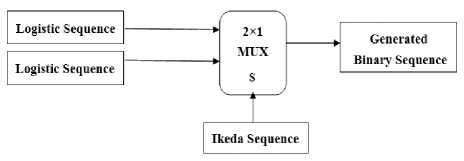
Fig.3. Proposed algorithm to generating Pseudo Random binary sequence.

• V. Chaotic Permutation algorithms

In this paper two permutation algorithms has been used that were proposed in the previous paper of authors. These two algorithms are discussed as follow.

• A.    Permutation algorithm based on traditional Japanese game called Amidakuji

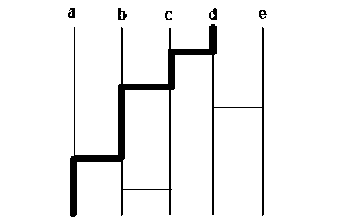
The main idea of this method is taken from a Japanese traditional lottery game known as “Amidakuji” or “ghost leg”. Amidakuji is a lottery policy where rule-less pairings between two sets of any number of something are made, as long as the number of things in each set is the same. This is often used in Japan to allocate a number of prizes to the same number of persons. It consists of columns (vertical lines) with bars (flat lines) that interact with two adjacent vertical lines. This is shown in Fig.4 for Player “d”.

cellphone TV watch Laptop Calculator

Fig.4. Amidakuji game

He will go down during the column. When he reaches a bar, he follows that line. The player then goes down to the adjacent column and repeats this process. In this case, Player “d” will receive the “cellphone”. The permutation problem is defined as the problem of finding a description of a function that performs a certain permutation. Various descriptions can be candidates for this problem. Among them, the Ladder Network serves as a suitable function description for our purposes: it performs permutations, and it incorporates neutral factors.

• B.    Rapid Permutation Algorithm

Here, we use these two algorithms with the pseudorandom sequence generator proposed in this paper. The permutation pattern of these algorithms is produced by proposed pseudo-random sequence generator.

• VI.    Proposed Image Encryption Algorithm

We implement this algorithm for gray scale images with 8 bits color depth. The dimension of test images is 256×256 pixel. For example we select “camera man” image for simulating our algorithm. First, we count number of ones in binary form of image pixels and then we produce a pseudo random sequence with length of 256×256×8 bits that is in follow interval:

[number of ones, number of ones + 256×256×8]

We store this sequence in an array called K. Considering that the probability that number of ones in binary representation of two different image is equal is very low and this sequence is unique for each image. After generating this pseudo random sequence, binary form of each pixel is permuted based on Rapid Permutation Algorithm with permutation pattern generated by proposed PRBG. After this step the source image of “camera man” changes. In Fig.5, visual compare of these two image is shown.

As can be seen, the texture of the source image can still be seen in the encrypted image

Fig.5. Source image and encrypted image after chaotic permutation of pixels.

To solve this problem, the binary representation of each pixel is XORed bit-by-bit with 8 consecutive bits of sequence K. After this step, the texture of the source image cannot be seen in the encrypted image. The encrypted image after this step is shown in Fig.6.

Fig.6. Encrypted image after XOR operation

So far, only the confusion stage has been performed on the source image.

In this stage, the diffusion process must be done. This means that the order of pixels will change. For this purpose, each row and column of the obtained image from the previous step be scrambled. We show our proposed method for one row of image.

Each row consists of 256 pixels. For scrambling, we divide them into four parts. Thus, we have four sets of 64 pixels. Now, we permute each set of pixels with Amidakuji algorithm. The keys of each sets are equal. After this step, we shuffle permuted sets such that has been shown in Fig.7.

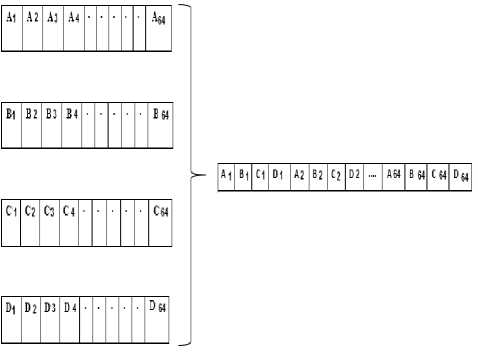
Fig.7. Shuffling process of permuted sets

After all rows, we permute and scramble all column.

The encrypted image after this step is shown in Fig.8.

Fig.8. The final encrypted image

The flowchart of proposed algorithm is shown in Fig.9.

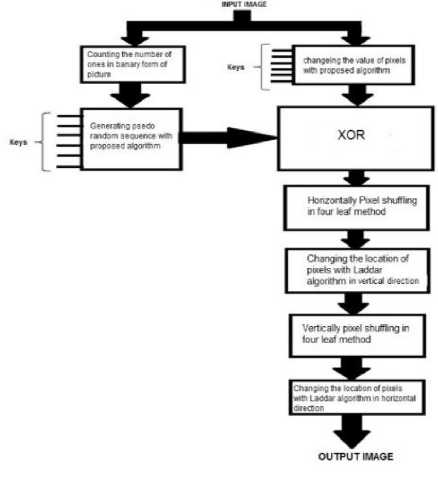
Fig.9. Flowchart of proposed algorithm

• VII.    Experimental Results

• A. Key Space

In an encryption algorithm, the key space must be sufficiently large to demonstrate its strength against different attacks. The key space size is equal to the total number of keys used in the algorithm. In fact, the strength of a comprehensive brute force attack depends on the size of the key space. In an exhaustive brute-force attack, the attacker tests all possible keys, so if the key space is large enough, the possibility of success would be too low. In this algorithm, keys are the initial values of the chaotic map that has been used in the algorithm. Six keys in this method are used. If the precision is 10–14, the size of the key space for the initial condition and control parameter of the proposed scheme is 2 14×6. This size of the key space is large enough to defeat a brute-force attack by any super computer today.

B. Visual Test and Histogram Analysis

It is important to ensure that encrypted and source images do not have statistical similarities in order to prevent the leakage of information from an encrypted image, and the histogram of an encrypted image should be significantly different from the original image and usually with a uniform distribution. The histogram analysis explains that how pixels in an image are distributed by plotting the number of pixels at each intensity level.

Fig.10 shows the histograms of original images. In fig.10 histogram analysis of encrypted images using proposed algorithm is shown. As shown in fig.10, the histogram of plain images contains sharp rises followed by sharp declines and the histogram of encrypted images in fig.11 has uniform distribution which is significantly different from original images and has no statistical similarity in appearance.

C. Correlation Analysis

In a plain image, two adjacent pixel are strongly correlated vertically, horizontally and diagonally. The correlation coefficient of two adjacent pixels in horizontal, vertical and diagonal orientations is calculated by following equations.

1 ^N

E ( x ) = ~E x.

1 ^N

D ( x ) = -S( x. — ^E ( x )) 2 N tl

1N cov(x, y)   ^ V (x.

- E ( x ))( y i - E ( y ))

i = 1

Image

Original Image

ra Man

Lena

Histogram

r xy

cov( x , y )

D ( x ). D ( y )

The maximum correlation coefficient value is one, and the minimum value is zero. In Table 2 the correlation coefficients for two plain images are shown. It can be seen that the use of the proposed encryption algorithm significantly reduces the correlation coefficients. In Table 2 we compare the correlation coefficient of our proposed algorithm with some algorithms proposed in other papers.

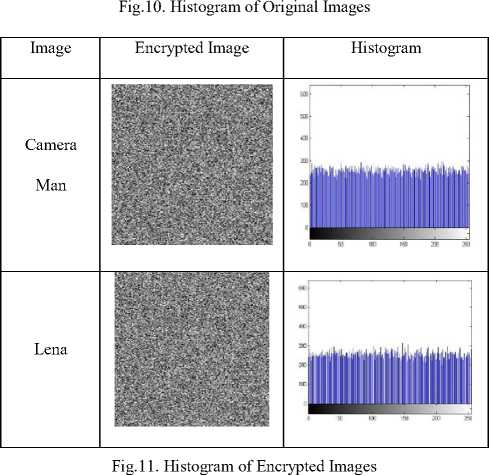
Table 2. Correlation coefficients of different algorithms

s	E f Hi	£ E "5 5S p	£ fc E "5 5 s p	E | | f § 1 E-g 1 US |-5	E 1 £ ^1 и 5 |-5
и	0.0038	-	-	-	-
		0.00312(H)	0.0021(H)	0.0058(H)	0.0020(H)
	0.0015	-0.00317(V)	0.0027(V)	0.0061(V)	0.0018(V)
		-0.00310(D)	0.0018(D)	0.0059(D)	-0.0015(D)

D. Informat on entropy analys s

Entropy is a random statistic parameter that can be used to characterize an image’s texture. The highest entropy value of a cipher image is 8, which means the encrypted image cannot be decrypted by changing the secret key slightly. In table 3 two plain image entropies and their encrypted images are shown.

The results of table 3 show that the entropies of encrypted images are closer to 8.

Table 3. Information entropy of different algorithms

Image	Entropy of plain image	Entropy of encrypted image with our proposed algorithm	Entropy of encrypted image with proposed algorithm in Ref.[17]	Entropy of encrypted image with proposed algorithm in Ref.[18]	Entropy of encrypted image with proposed algorithm in Ref.[19]	Average Entropy of encrypted image with proposed algorithm in Ref.[23]
Camera Man	7.0134	7.9970	7.9939	-	7.9985	7.9993
Lena	7.5954	7.9964	7.9975	7.9888	7.9963	7.9993

M x N

MN

XX D(i, j) x100% i=1 j=1

E. Differential Attack Analysis

An image encryption algorithm needs to be sensitive to plain image changes. This means that if one pixel of the plain image is altered, the differences between two cipher images will be obvious. In other words, to withstand a differential attack, a minor change in the plain image should cause a fundamental change in the cipher image. This is a measurement of the sensitivity of the plain image that can be achieved using the following method. First, a plain image P1 encrypted with proposed algorithm to a cipher image C1. Then a pixel in plain image is selected randomly and its value is changed to have a small change. In this paper, this change is done by toggling Most Significant Bit (MSB) of randomly selected pixel. The modified image P2 is encrypted using the same key to generate a new cipher image C2. The two cipher images C1 and C2 are then compared quantitatively using the following measures[16].

1. Number of pixels change rate (NPCR): This parameter shows the percentage of different pixels between the two cipher images C1 and C2 using the following equation:

NPCR =

In (11) if C1(i,j)=C2(i,j) then D(i,j)=1 otherwise D(i,j)=0 and M and N represent the width and height of the test images.

2. Unified Average Changing Intensity (UACI): This is a measure of the average intensity of differences between the cipher images C1 and C2, as defined by:

UACI =

M x N

MN

XX i=1 j=1

I C 1( i , j ) - C 2( i , j )| 1——---—x100%

2 n - 1

In (12) n is the bits of the pixels.

If n = 8, the ideal NPCR and UACI values are 99.6094% and 33.4635%, respectively[15].

The NPCR and UACI of two image is given in the Table 4. We note that the proposed algorithm has the best performance among the considered algorithms including those in table 4.

Table 4. NPCR and UACI values of different images by different algorithms

		Calculated Values with Proposed algorithm	Calculated Values in Ref.[17]	Calculated Values in Ref.[19]	Calculated Values in Ref.[11]	Calculated Values in Ref.[20]
Camera Man	NPCR	0.9963	0.990039	0.9963	-	-
	UACI	0.3346	0.331026	0.3359	-	-
Lena	NPCR	0.9962	0.995193	0.9960	0.99609	0.9961
	UACI	0.3359	0.335851	0.3347	0.3346	0.3347

• VIII.    Conclusion

We proposed a new algorithm for image encryption based on chaotic permutation. It uses a previous chaotic map, Logistic map and Ikeda map to generate pseudorandom bits and uses this pseudo-random sequence to permute the value and order of pixels with two novel permutation algorithms. The performance analysis includes key space analysis, visual and histogram analysis, correlation analysis, the percentage of unchanged pixels, information entropy analysis and differential attack analysis, which are performed numerically and visually. Based on the performance analysis, we conclude that the proposed method is useful for secure image encryption.