A New Video Compression Method using DCT/DWT and SPIHT based on Accordion Representation

Published Online May 2012 in MECS DOI: 10.5815/ijigsp.2012.04.04

The main intention of video coding in most video applications is to reduce the amount of video signal for storing and/or transmission purposes without affecting its visual quality. On root of quality, disks capacity and bandwidth the desired video performance can be achieve. For portable digital video applications, highly-integrated real-time video compression and decompression solutions are required. In reality motion estimation based encoders are the most usually used in video compression techniques. Such encoders make use of inter-frame correlation to provide well-organized compression. On the other hand Motion estimation process is computationally expensive; its real time implementation is tricky and pricey [1][2].

For stored video applications, motion-based video coding standard MPEG (Moving Picture Experts Group) was principally urbanized, where the encoding process is typically carried out off-line on powerful computers. So it is less suitable to implement as a real-time compression technique for a portable recording or communication device (video surveillance camera and fully digital video cameras). In such applications, efficient low cost/complexity implementation is the most noteworthy issue. Thus, researchers turned towards the design of new coders more adapted to new video applications requirements which leads some researchers to look for the exploitation of 3D transforms in order to exploit temporal redundancy.

3D transform coder produces video compression ratio which is close to the motion estimation based coding one with less complex processing [3][4][5][6]. Redundancy has not the same pertinence since the efficiency of 3D transform can reduce as pixel’s values variation in spatial or temporal dimensions is not uniform. Often the temporal redundancies are more relevant than spatial one [3]. In order to achieve efficient compression by exploiting more and more the redundancies in the temporal domain; this is the basic purpose of the proposed technique. The proposed technique consists on projecting temporal redundancy of each group of pictures into spatial domain to be combined with spatial redundancy in one representation with high spatial correlation. The obtained representation will be compressed as still image with JPEG coder.

The rest of the paper is organized as follows: Section 2 gives an overview of basics of DWT based video compression techniques. In section 3 we review the basics of the proposed technique and the extensions chosen to improve the compression ratio. This is the main contribution of this work. Section 4 presents the results of a comparative study between compression standards with the proposed technique. Section 5 gives some analysis and comments about the technique. The last section concludes this paper with a short summary.

• II.    DCT BASED CODING TECHNIQUES

The transform coding developed more than two decades ago, has proven to be a very effective video coding technique, especially in spatial domain. Today, it forms the basis of almost all video coding standards. The most common transform based intra-frame video coders use the DCT (Discrete Cosine Transform) which is very close to JPEG. The video version is called MJPEG, where the “M” stands for “motion”. The input frame is first segmented into N X N blocks. A unitary space-frequency transform is applied to each block to produce an N X N block of transform (spectral) coefficients that are then suitably quantized and coded.

The main goal of the transform is to de-correlate the pixels of the input block. This is achieved by redistributing the energy of the pixels and concentrating most of it in a small set of transform coefficients. This is known as Energy compaction. Compression comes about from two main mechanisms. First, low-energy coefficients can be discarded with minimum impact on the reconstruction quality. Second, the Human vision system has differing sensitivity to different frequencies. Thus, the retained coefficients can be quantized according to their visual importance. The DCT, which will be used in our video compression approach, is widely used in most modern image/video compression algorithms in the spatial domain (MJPEG, MPEG).

Although it is efficient, it produces some undesirable effects; in fact, when compression factors are pushed to the limit, three types of artifacts start to occur: “graininess” due to coarse quantization of some coefficients, “blurring” due to the truncation of high-frequency coefficients, and “blocking artifacts,” which refers to artificial discontinuities appearing at the borders of neighboring blocks due to independent processing of each block [7]. Moreover, the DCT can be also used in the temporal domain: In fact, the simplest way to extend intra-frame image coding techniques to inter-frame video coding is to consider 3-D waveform coding. The 2D-DCT has the potential of easy extension into the third dimension, i.e. 3D-DCT. It includes the time as third dimension into the transformation and energy compaction process [3][4][5][6]. In 3-D transform coding based on the DCT, the video is first divided into blocks of M N K pixels (M; N; K denote the horizontal, vertical, and temporal dimensions, respectively). A 3-D DCT is then applied to each block, followed by quantization and symbol encoding, as illustrated in Fig. 1. A 3-D coding technique has the advantage that it does not require the computationally intensive process of motion estimation. However, it presents some disadvantages; it requires K frame memories both at the encoder and decoder to buffer the frames. In addition to this storage requirement, the buffering process limits the use of this technique in real- time applications because encoding/decoding cannot begin until all of the next K frames are available.

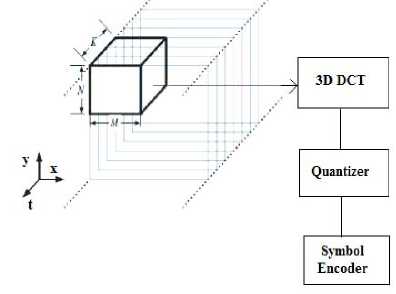
Figure 1. 3D DCT Video Compression

Moreover, the 3D DCT based video compression technique produce some side effects in low bit rates, for example the effect of transparency produced by the DCT 3D [8]. This artifact is illustrated by Fig. 2. The image shown in Fig. 2, is a frame in a video compressed with MPEG, in which DCT was used.

Figure 2. Transparency effect in 3D DCT

The techniques of transformed 3Ds were revealed since 90s, but the research in video compression was oriented towards the coding based on motion estimation. The design tendency of new coding diagrams led some researchers restarting the exploitation of transformed 3Ds in video compression. The coders based on this type of transformation produce high compression ratio with lower complexity compared to motion compensated coding. 3D DCT based video compression techniques treat video as a succession of 3D blocks or video cubes, in order to exploit the DCT properties in both spatial and temporal dimensions. The proposed coding technique will be based on the same vision. The main difference is how to exploit temporal and spatial redundancies. Indeed, the proposed technique puts in priority the exploitation of temporal redundancy, which is more important than the spatial one. The latter assumption will be exploited to make a new representation of original video samples with very high correlation. The new representation should be more appropriate for compression. Detailed description will be presented in the next section.

• III.    PROPOSED APPROACH

The basic idea is to represent video data with high correlated form which can be achieved by exploiting both temporal and spatial redundancies in video signal. The input of our encoder is so called video cube, which is made up of a number of frames. This cube will be decomposed into temporal frames which will be gathered into one frame (2 dimensions). The final step consists of coding the obtained frame. In the following, we detail the technique design steps.

• A.    Hypothesis

Many experiences had proved that the variation of the 3D video signal is much less in the temporal dimension than the spatial one. Thus, pixels, in 3D video signal, are more correlated in temporal domain than in spatial one [3]; this could be traduced by the following expression: for one reference pixel I (x,y,t) where:

• I :    pixel intensity value

• x,    y: space coordinate of the pixel

• t:    time (video instance)

We could have generally:

I (x;y;t) - I (x;y;t +1) <  I (x;y;t) - I (x + 1;y;t) (1)

This assumption will be the basis of the proposed technique where we will try to put pixels - which have a very high temporal correlation - in spatial adjacency.

• B.    “Accordion” based representation

To exploit this succeeding assumption, we start by carrying out a temporal decomposition of the 3D video signal, the Fig. 3 shows temporal and spatial decomposition of one 8X8X8 video cube:

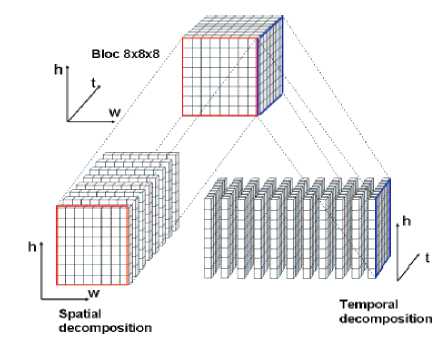
Figure 3. Spatial and temporal decomposition principle

“Frames” obtained from the temporal decomposition is called temporal frames. These latter are formed by gathering the video cube pixels which have the same column rank. According to the mentioned assumption, these frames have a stronger correlation compared to spatial frames. In turn to increase correlation in Accordion Representation we reverse the direction of even frames.

Fig. 4 illustrates the principle of this representation. Thus, the “Accordion representation” is obtained as follows: first, we start by carrying out a temporal decomposition of the video 3D. Then, the even temporal frames will be turned over horizontally (Mirror effect). The last step consists of frames successively projecting on a 2D plan further called "IACC" (Inverse Accordion) frame.

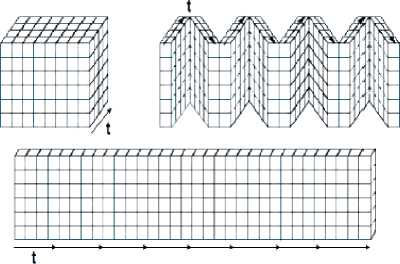
Figure 4. ACCORDION Representation

Fig. 4 illustrates the principle of this representation. The “Accordion representation” tends to put in spatial adjacency, the pixels having the same coordinates in the different frames of the video cube. These representations transform temporal correlation in the 3D original video source into a high spatial correlation in the 2D representation ("IACC"). The goal of turning over horizontally the event temporal frames is to more exploit the spatial correlation of the video cube frames extremities. In this way, “Accordion representation” also minimizes the distances between the pixels correlated in the source. That’s could be clearer in Fig. 5 and Fig. 6.

• C.    “Accordion” analytic representation

The “Accordion representation” is obtained following a process having the GOP frames (I 1..N) as input and has as output the resulting frame IACC. The inverse process has as input the IACC frame and as output the coded frames (I 1..N). The analysis of these two processes leads to the following algorithms. The algorithm 1 describes how to make “Accordion representation” (labeled ACC). The algorithm 2 represents the process inverse (labeled ACC-1).

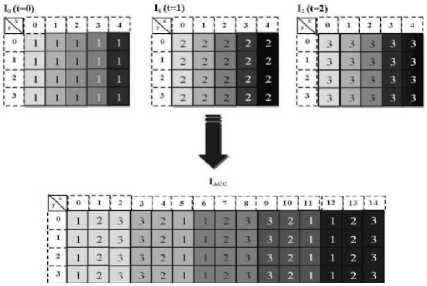
Figure 5. ACCORDION representation example

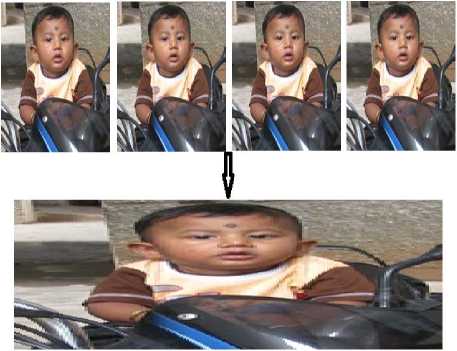
Figure 6. ACCORDION representation another example: Munna on Bike Sequence

Let us note that:

• 1)    L and H are respectively the length and the height of the video source frames.

• 2)    NR is the number of frames of a GOP (Group of Picture/Frames).

• 3)    IACC(x; y) is the intensity of the pixel which is situated in "IACC" frame with the co-ordinates x,y according to “Accordion representation” repair.

• 4)    In(x; y) is the intensity of pixel situated in the Nth frame in original video source.

We can also present the “Accordion Representation” with the following formulas:

ACC formulas:

IACC = In(xdivN; y) (2) with n=((x div N)mod2)(N-1)+1-2((x div N)mod 2)(x modN) ACC inverse formulas:

In(x; y) = IACC(XACC; y) (3) with

XACC=((x div N)mod 2)(N-1)+n(1-2('x div N) mod2))+x

In the following, we will present the diagram of coding based on the “Accordion representation”.

• D.    ACC – JPEG Coding

ACC - JPEG Coding, as depicted in Fig. 7, was preceded as follows:

• 1)    Decomposition of the video in groups of frames (GOP).

• 2)    “Accordion Representation” of the GOP.

• 3)    Decomposition of the resulting "IACC" frame into 8x8 blocks.

• 4)    For each 8x8 block:

• -    Discrete Wavelet Transformation (DWT).

• -    Quantification of the obtained coefficients.

• -    Course in Zigzag of the quantized coefficients.

• -    Entropic Coding of the coefficients (RLE, Huffman)

• E.    SPIHT CODING

The powerful wavelet- based image compression method called Set Partitioning in Hierarchical Trees

(SPIHT). The method deserves special attention because it provides the following

• •    Good image quality, high PSNR, especially for color images.

• •    It is optimized for progressive image transmission

• •    Produces a fully embedded coded file

• •    Simple quantization algorithm

• •    Fast coding/decoding(nearly symmetric)

• •    Has wide applications, completely adaptive

• •    Can be used for lossless compression

• •    Can code to exact bit rate or distortion

• •    Efficient combination with error protection

Algorithm 1 Algorithm of ACC:

• 1:    for x from 0 to (L * N) - 1 do

• 2:    for y from 0 to H - 1 do

• 3:               if ((x div N) mod 2) != 0 then

• 4:                 n=(N-1) - (x mod N)

• 5:                  else

• 6:               n=x mod N

• 7:                end if

• 8:               IACC(x; y)= In (x div N,y)

• 9:    end for

• 10:    end for

Algorithm 2 Algorithm of ACC-1:

• 1:    for n from 0 to N - 1 do

• 2:    for x from 0 to L - 1 do

• 3:               for y from 0 to H - 1 do

• 4:                        if (x mod 2) != 0 then

• 5:                      XACC= (N -1) - n (x*N)

• 6:                            else

• 7:                     XACC= n(x * N)

• 8:                          end if

• 9:                     In(x,y)=IACC(XACC; y)

• 10:              end for

• 11:    end for

• 12:    end for

  Input video

  
  

Frame separat ion

Acco rdion

D W T

Quanti zation

Inverse quantiz ation

Inverse DWT

Inverse

Accordio

Decoded frames

n

• Figure 7. ACC - JPEG coding

The SPHIT process represents a very effective form of entropy-coding. For lossless compression we proposed an integer multi resolution transformation similar to wavelet transform, which we called S+P transform. It solves the finite-precision problem by carefully truncating the transform coefficients during the transformation (instead or after). A codec that uses this transformation to yield efficient progressive transformation up to lossless recovery is among the SPHIT yields progressive transmission with practically no penalty in compression applies to lossless compression too.

IV.Experiments

Many experiments had been conducted in order to study the performances of our technique by considering different kinds of videos. In the following, we summarize the experimental results with some analysis and comments.

• A.    parameters of the representation

We start by studying the performances of the proposed technique with different NR values, it's pointed out that NR presents the number of frames of the video cube that forms the "IACC" frame. The best compression rate is obtained with NR=8. Since JPEG process starts with breaking up the image into 8x8 block, the “Accordion representation” does not have any interest with a GOP made up more than 8 frames. Fig. 8 presents ACC-JPEG PSNR curves variation according to used NR parameter for “Munna on Bike” sequence (CIF 25Hz). These results reveal the NR influence on ACC-JPEG compression performance. By multiplying the NR value by 2, the PSNR increases from 1 to 2 dB. By increasing the GOP’s frames number there is compression improvement this is due to the exploitation of the temporal redundancies. For NR=1, it acts as the MJPEG which does not exploit the temporal redundancies. Better compression performance can be achieved by increasing the value of NR, so that the coder exploits more temporal redundancies.

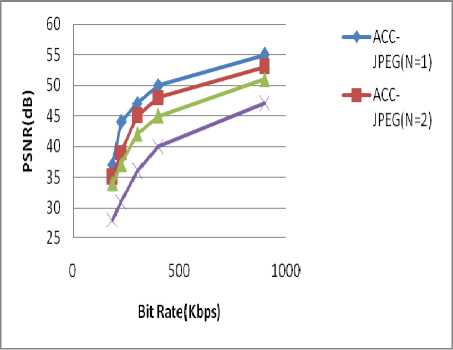
Figure 8. ACC-JPEG PSNR curve variation according to NR parameter

• B.    Compression performance

  In all studied sequences, the ACC-JPEG outperforms the MJPEG in low and high bit rates; it outperforms MJPEG 2000 in high bit rates (from 750 kbs) and it starts reaching the MPEG 4 performance in bit rates higher than 2000 Kb/s. Among the studied sequences, we have got bad compression performance with “Foreman” sequence. The “Foreman” sequence contains more motion than the other studied sequences. This sequence contains non-uniform and fast motion which is caused by the camera as well as the man's face movement.

The ACC-JPEG efficiency decreases, measured PSNR is relatively low with an alternate character, especially in low bit rate. In fact, such results are expected as ACC-JPEG eliminates "IACC" frame's high frequency data which actually represent the high temporal frequency produced by the fast motion in the Foreman sequence. “Hall monitor” sequence seems to involve less motion compared to the Foreman sequence; the motion takes place only in a very concentrated area. Due to the little amount of motion taking place on the overall image, we observed that our technique get better results. Fig. 10 shows results of PSNR based comparative study between ACC-JPEG and different existing video compression standards relative to “hall monitor” sequence. The best results were given with “Munna on Bike” sequence (Fig. 6); “Munna on Bike” is a low motion sequence. The motion is confined to the person's lips and head. Since motion is low, temporal redundancy is high and it is expected that ACC-JPEG becomes efficient. Another result, i.e. 2D version of a video was shown in Fig. 9.

Figure 9. 2D version of a video

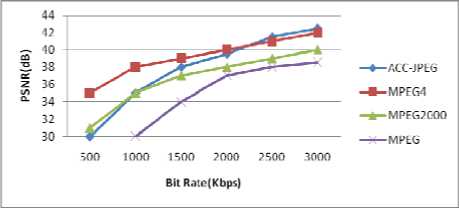
Figure 10. PSNR evaluation (Hall monitor)

• C.    ACC-JPEG artifacts

In the proposed technique, the DWT is exploited in temporal domain. Some artifacts produced by DWT based compression techniques [9][10] persists in ACC-JPEG. Actually, the application of the DWT on IACC allows the transformation from the spatial domain to the frequency domain. After quantification process, we will eliminate the high spatial frequencies of "IACC" frame which actually present the high temporal frequencies of the 3D signal source. Thus, a strong quantification will not affect the quality of image but will rather affect the fluidity of the video. The change in the value of a particular pixel from one frame to another can be interpreted as a high frequency in the time domain.

Once some of the coefficients have been quantized (set to zero) the signal is smoothed out. Thus some fast changes over time is somewhat distorted which explain the alternate character of the ACC-JPEG PSNR waveform shown in Fig. 11. However, some sudden pixels change will be eliminated. This will offer a useful functionality such as the noise removal; indeed, the very high temporal frequency (sudden change of a pixels value over time) is generally interpreted as a noise. Moreover, some artifacts existing in DWT based compression techniques such as spatial distortions generated through the massive elimination of the high spatial frequencies (macro-blocking) does not exist in the proposed technique.

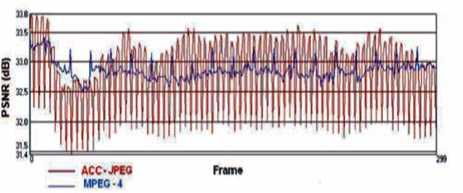
Figure 11. PSNR waveform comparison between ACC-JPEG and MPEG-4

This will offer a useful functionality such as the noise removal; indeed, the very high temporal frequency (sudden change of a pixels value over time) is generally interpreted as a noise. Moreover, some artifacts existing in DWT based compression techniques such as spatial distortions generated through the massive elimination of the high spatial frequencies (macro-blocking) does not exist in the proposed technique as shown in Fig. 12. The PSNR Curve relative to the ACC -JPEG coding is in continuous alternation from one frame to another with a variation between 31.4 dB and 33.8 dB unlike MPEG PSNR which is almost stable. In one hand, ACC-JPEG affects the quality of some frames of a GOP, but on the other hand, it provides relevant quality frames in the same GOP, while MPEG produces frames practically of the same quality. In video compression, such feature could be useful for video surveillance field; generally, we just need some good quality frames in a GOP to identify the objects (i. e. person recognition) rather than medium quality for all the frames.

• V. Conclusions

Generally, video signal has high temporal redundancies between a number of frames and this redundancy has not been exploited enough by current video compression techniques. In this explore, we suggest a new video compression technique which exploits objectively the temporal redundancy. With the apparent gains in compression efficiency we predict that the proposed technique could open new horizons in video compression domain. So, it strongly exploits temporal redundancy with the minimum of processing complexity which facilitates its implementation in video embedded systems.

It presents some useful functions and features which can be exploited in some domains as video surveillance. In high bit rate, it gives the best compromise between quality and complexity. It provides better performance than MJPEG and MJPEG2000 almost in different bit rate values. Over .2000kb/s. bit rate values our compression technique performance becomes comparable to the MPEG 4 especially for low motion sequences. There are various directions for future investigations. First of all, we would like to explore other possibilities of video representation. Another direction could be to combine “Accordion representation” with other transformations such as wavelet transformation. The latter allows a global processing on the whole of the “Accordion representation”, on the contrary of the DWT which generally acts on blocks.