A Novel Algorithm for Minutiae Matching

• I.    INTRODUCTI O N

  Biometrics is the field of science which invol v es recognizing humans automatically via uni q ue characteristics. Recognizing humans b y means of t h eir fingerprint impression is the mos t widely u s ed biometrics today. The fingerprint reco g nition starte d in 1600s, but the use of biometrics is expanding v e ry rapidly. Fin g erprints have been used w i dely in lapto p s, computers, enterprises, to college buildings e tc. Fingerprint r ecognition is used as a m eans to rest r ict the unauthorized users from accessing u seful data.

Fingerprint contains complex patterns of stripes, called ridges. There exists some gap between the ridges, called valleys. A ridge can spread further in two ways, either it ends or bifurcates into two ridges. The place where ridge ends is called termination or ridge end and where it bifurcates is called bifurcation. Minutiae consist of these two basic types, ridge end and bifurcation. The overall fingerprint recognition consists of three steps:-

• a.    Image Preprocessi n g

• b.    Minutiae detection a nd Feature e x traction

• c.    Minutiae matching

Image pre p rocessing is t he first step of fingerprint matching. It is done to make image clearer to understand. In this, three s teps are involved, Image Quality Enhancement, Bin a rization and Thinning. In image quality enhancemen t phase the q uality of the given image is improved so t hat the imag e will be good e n ough for fur t her processi n g. The binarization of the gray scale ima g e converts i t to black and white image. A threshold is selected and applied to e a ch pixel. The pixels above t h reshold are assigned bla c k and below t h reshold are assigned whit e . In thinning , the width of e a ch ridge is r educed to o n e pixel by u sing various methods. Cent r al line thinni n g is advised.

Minutiae d etection an d feature e x traction step i n volves refini n g of the th in ned image, detecting the minutiae poin t s and then extracting f eatures from image. In Det e ction, the w hole image i s scanned to detect the ridge ends and b ifurcations. I n Extraction, t h e coordinates, the angle o f orientation a n d the type of minutiae is co m puted for ea c h minutiae p o int.

Minutiae matching, the third step involves matching the template image with the input image. Template image is collected at the time of enrollment and stored in the database. During recognition phase, the input image is compared against template image. This phase decides whether the two images are from the same finger or from different fingers.

We are g oing to propose a novel a l gorithm for t he last step i.e. minutiae matching. The b a sic idea beh i nd our algorithm is to draw all possi b le number of polygons by joining all detected min u tiae points o f a given image. This is done for both the template im a ge and the inp u t image. Then the polygo n s of one im a ge are overlap p ed on other image such that maxim u m numbers of p olygons coincide.

Fig 1: Template image

Two polyg o ns can be c ompared fo r equality by simply considering the leng th of sides an d angles made by two sides.

Fig 2: Input image

We can say p o lygon-1 and polgon-2 ar e same if the

following conditions are tru e .

AB = PQ, BC = QR, CD = RS, DE = ST, EF = TU, AF = PU and a = p, b = q, c = r, d = s, e = t, f = u

This is all a bout our al g orithm and w e match two fi n gerprint sa m ples on th i s idea. Tw o fingerprints match only when they fo r m similar p o lygons after joining the minutiae points.

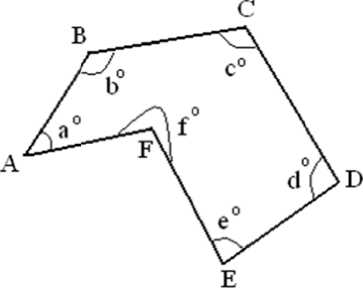
Fig 3: po l ygon-1

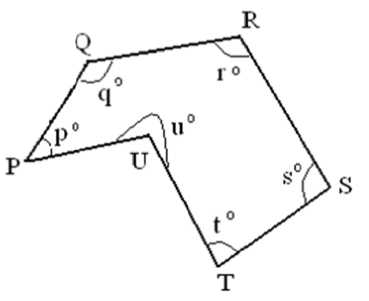
Fig 4: po l ygon-2

• II.    P R IVIOUS WORK DONE O N MINUTI A E MATCHING

A lot of work has been done suc c essfully in t h is area in past. One of the most widely u sed method s is [3,1] to cre a te a matrix, called rota t e value , of t he orientation a ngle difference between each templ a te minutiae, T k (1≤k≤NT) , and each in p ut minutiae, I m (1≤m≤NI) . Here, NT and NI represent t he total num b er of minutiae i n the template and input s e ts, respectiv e ly. The value at rotate values (k,m) represents t he difference b e tween the orientation angl e s of T k and I m .

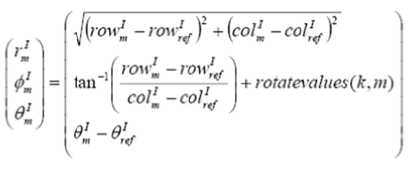
The above formula is used to cal c ulate the ra d ial distance, radial angle and the orientat i on for templ a te image and the input image. Then these values a re compared among the minutiae points, one point fr o m template and one from input imag e , with cert a in threshold va l ue to find the matching po i nts.

Another m ethod called focal point [ 5 ] considere d as reference po i nt is chosen that is design e d as a cente r of moment in polar coordinate for the fingerp r int matching method. The focal point fo r any type of fingerprint images can be identified a nd tested w ith various orientation, elastic distortion and noise.

Another a pproach for minutiae mat c hing is done by calculating the differences of spatial a n d orientation of minutiae [6] .

Fingerpri n t minutiae can be matched by using b o th the local a n d global structures of minutiae [7]. T he local structure of a minutia describes a rotation a nd translation i nvariant feature of the minutia in its neighborhood. It is used to find the co r respondence of two minutia e sets and increase the reliability of t he global matching. The global struct u re of minut i ae reliably dete r mines the uniqueness of fi n gerprint.

According to He et al.’s [8] matchi n g algorithm u se of a variable sized bounding box mak e s the match i ng algorithm more robust to non-linear deformat i on between fingerprint images.

Another interesting technique was proposed [9], where the minutiae points are connected using a Delaunay triangulation and analyzes the relative position and orientation of each minutia with respect to its neighbors obtained by the triangle structure. Two fingerprints are considered matching, if their triangle structures are similar according the neighbor relationship.

Shi et al. [10] introdu c ed two glo b al statistical features of fin g erprint imag e , including t h e mean ridge width and the normalized quality esti m ation of the whole image, and prop o sed a nov e l fingerprint matching algo r ithm based o n minutiae sets combined with the globa l statistical f e atures. This a lgorithm has a d vantage of both local and global features in fi n gerprint matching.

Xuefeng Li a ng and Tets u o Asano [1 1 ] proposed a minutia polygons algorithm t ha t is used to m atch distorted fingerprints. A minutia poly g on describes not only the minutia type an d orientation b u t also the min u tia shape. This technique empl o ys an impro v ed distortion m odel using a Multi-quadric b a sis function with paramet e rs. Adjustable parameters mak e this model m ore suitable for fingerprint distortion.

• III.    PROPOS E D ALGORI T HM

For our pr o posed algor it hm we nee d to store the c o ordinates of the detected minutiae an d the types of minutiae.

TABLE I. TH E EXTRACTED F ORMAT CAN B E SEEN AS FOLL O WS

Absolute co ordinate	Minutiae Type
79,10 2	Bifur c ation
75,21 4	Ridg e End
64,11 0	Bifur c ation
157,1 8 2	Ridg e End

T h ese details a re stored for the template and the input image. From t h ese two sets of attributes our algorithm decides wheth e r the image s are from s a me finger or from different f inger. The d e tail about th e algorithm is e x plained in th e next sectio n .

• IV.    IL L USTRATIO N OF THE P R OPOSED AL G ORITHM

Let us say t he total no. o f minutiae i n the template is 5 and the tot a l number of m inutiae in t h e input image is 8. The algorithm works as follows.

TABLE II. FOR TEMPLAT E

Name	Co ordinate	Radial Distance	Minutiae Type
A	79,102	0	Bifurcatio n
B	75,214	112	Ridge end
C	64,110	17	Bifurcatio n
D	157,182	111	Ridge end
E	50,255	156	Bifurcatio n

TABLE III. FOR INPUT IMA G E

Name	Co ordinate	Radial Distance	Minutiae Type
P	75,103	0	Bifurcation
Q	87,90	18	Bifurcation
R	172,146	106	Ridge end
S	108,206	108	Ridge end
T	101,254	153	Bifurcation
U	224,228	194	Ridge end
V	187,52	123	Ridge end
W	231,133	159	Ridge end

The radial distance is calculated usin g the follow i ng formula.

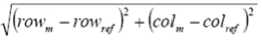
The radi a l distance is the distance o f the coordin a te from a chosen reference point. So if th e reference p o int and the co o rdinate are the same, t hen the ra d ial distance will be zero.

During p airing the minutiae we m ust be careful about the type of minutiae (Ridge a n d Bifurcatio n ). Bifurcations should be paired with bif u rcation of ot h er image and t he same is for ridges. L et us pair t he reference point ‘A’ of template i m age with t he reference point ‘P’ of input ima g e. Now ot h er calculations are as follows.

Calculati o n of Angles made be t ween minut i ae points with the reference point as cente r . Angles can be easily calcul a ted from the coordinates o f three points.

TABLE IV. FOR TEMPLAT E

A	B	C	D	E
B	--	60°	46°	9°
C	6 0 °	--	106°	51°
D	4 6 °	106°	--	55°
E	9°	51°	55°	--

T ABLE V. FOR I NPUT IMAGE

P	Q	R	S	T	U	V	W
Q	--
R	71°	- -
S	120°	4 8°	--
T	128°	5 6°	8°	--
U	87°	1 6°	32°	40°	--
V	23°	4 8°	97°	105°	64°	--
W	58°	1 3°	61°	69°	29°	35°	--

Here the angle 71° represe n ts the angle R PQ = QPR= 71°. ‘P’ is th e chosen ref e rence point. So the angle represents the angle made b etween ‘Q’ a nd ‘R’ made with the refere n ce point ‘P’.

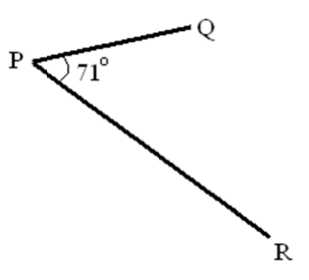
F i g 4: Figure sho w s the arrangeme n t of minutiae po i nts on the image

T h e following t able shows t h e result of matching of the minutiae point s on the basis o f radial dist a nce only.

TABLE V I. RADIAL DIS T ANCE COMP A RISON

Minutie Points of Template	Radial Distance from Reference point	Minutiae Points of Input image	Radial Distance from Reference point	Difference in radial distance
A	0	P	0	0
B	112	S	108	4
C	17	Q	18	1
D	111	R	106	5
E	1 5 6	T	153	3

If we set the threshold v a lue of difference between t h e radial dist a nces is 5, th e n all the ab o ve points are matched. So t he minutiae points paire d (Only radial distance is con s idered) till n o w are as foll o ws:

A – P B – S C – Q D – R E – T

Now let us compare the angles mad e by each p o int with other p o ints.

T ABLE VII. ANGLE COMPARI S ON

A/P	B/S	C/Q	D/R	E/T
B/S	--
C/Q	60 ° /120°	--
D/R	46 ° /48°	106°/71°	--
E/T	9° / 8°	51°/128°	55°/56°	--

Let us discuss in detail about the above table. It shows the a n gle CAB = 60° and the a n gle QPS= 12 0 °. But we ha v e the following pairs from the previ o us analysis.

A – P C – Q B – S

If this is t he scenario, then the angl e s must be sa m e. So this cont r adicts and it means ‘C’ m a y be a differ e nt minutiae po i nt and not the counterp a rt of ‘Q’. T he same condi t ion is for ‘B’ and ‘S’. The differe n ce between the angles is 120° - 60° = 60 ° . Let us say t he threshold value for angle difference is 5 °, and then t h is does not sati s fy the criteria.

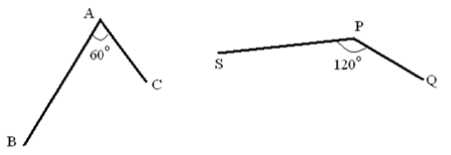
Fig 5: Figur e shows the arrangement of minu t iae points on the temp l ate image and the input image re s pectively

So if we calculate the difference bet w een angles w e find only th e following angles lie bel o w the thresh o ld value.

Angle DAB and angle RPS, difference i s 2°.

Angle EAB a nd angle TPS, difference is 1°.

Angle EAD a nd angle TPR, difference i s 1°.

This implies th e following p a irs are corre c t.

A – P

D – R

B– S

E – T

So we can c onclude that the given te m plate and the i n put image have only 4 mi n utiae points matched with ‘A’ as reference point in th e template im a ge and ‘P’ as reference point in the input i m age.

The abov e matched m inutiae po i nts can be d i agrammatica l ly viewed as follows.

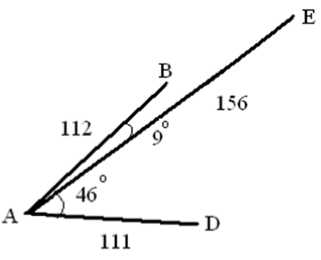
F ig 6: Figure sho w s the arrangem en t of all matche d minutiae points on the temp l ate image

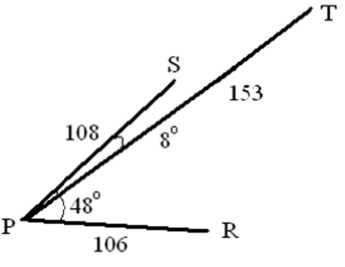
F ig 7: Figure sho w s the arrangem en t of all matche d minutiae points on the input image

We can see that all th e 4 minutia e points form similar structures in both th e template an d input image.

The same p rocedure is repeated for each chosen p a ir of refer e nce points. The highes t number of m atching point is the result.

• V.   T H E ALGORI T HM FOR M I NUTIAE

M A TCHING

• 1.    Repeat step-2 to step-5 until all minutiae points consumed.

• 2.    Take one minutiae point from template and one from input image as reference and repeat step-3 to step-4 until all minutiae points are consumed.

• 3.    Calculate radial distances for all points from the reference point for both the template and the input image.

• 4.    Pair one minutiae point from template with one from input image if the difference in radial distance of the points ≤ certain threshold value and their type are same.

• a.    If the above condition is true, then find the angle between two minutiae of an image made with the reference point. Find the same angle in other image.

• b.    If difference between the angles ≤ certain threshold value, then pair minutiae points from template and input image.

• 5.    Count the number of pairs (non repeating pairs) and this represents total number of matching minutiae points for a particular pair of reference points. Store the count value.

• 6.    Finally select the maximum count value. This is the final matching minutiae points.

• VI. CONCLUSION AND FUTURE WORK

We have developed an algorithm for minutiae matching on the basis of structural similarity of minutiae points on the finger print image. There are only two kinds of minutiae that are considered in the above algorithm, in fact various types of minutiae can be matched using the same algorithm. We have tested the algorithm and found it efficient to a great extent. The algorithm is tad slower than some other algorithm but gives better result. In future the time complexity of the algorithm can be reduced and the same algorithm can be used in applications other than fingerprint matching where 2D structural similarity is concerned.