A novel approach to design residue number system

Since the past decade, the computing industry has intensively tried to decrease the power consumption of portable systems. While lots of works have been done in this area, Residue Number System (RNS) has emerged as a viable nontraditional approach to increase the performance. The main functionality of RNS is that it decomposes complex arithmetic circuits into simpler ones [1]. Instead of performing large computations, every arithmetic’s such as long bit multiplication is broken down into little parallel modulo multiplications. Despite the advantages of the RNS based arithmetic systems, the usage of this system has been rather restricted. The main limit is the additional hardware required especially for conversion from RNS to binary number. Therefore, every work that aims to make this component smaller, faster and less power consumer leads to make the RNS system more efficient and practical.

So far, many reverse converters architecture has been offered [1-6] but some drawbacks still can be seen in those designs. They are designed independently of arithmetic unit. Moreover, the New CRT-II [2], being the one of the newest algorithms in reverse converter design, makes the reverse converter smaller than the previous designs, but slower due to the use of many modular CPAs. This paper aims to address these challenges by considering some properties that have been ignored in overall design of RNS systems.

The three-moduli set has interesting attributes and consequently has been widely investigated. However, extensions of this moduli set have been introduced in order to increase the Dynamic Range, such as the {2n - l,2n,2n + l,2n+1 - 1} [4] or {2k, 2n — 1, 2n + l,2n+1 - 1}, [2k, 2n — 1, 2n+l, 2”-1 - 1}[5], and [2n + 1, 2n - 1, 2n,22n+1 - 1} and {2n + 1, 2n - 1, 2n + l, 22n+i - 1} [6].

In this paper, by taking into account some properties of reverse converter, the last modular adder of the addition or multiplication in arithmetic unit are considered together with the reverse converter to increase the performance. The proposed method eliminates the last adder that is slow in arithmetic unit and replaces it with a faster adder in reverse converter. This strategy not only results in speed up but also in overall area reduction.

The Proposed Approach

The RNS is composed of three basic components: forward converter, arithmetic unit and the reverse converter [1]. However, there are limited works on all of these three components that has been considered together. In this paper for the first time, the reverse converter design is done based on the final modular adder of the arithmetic unit. It means that the final modular adder that has the same modulus as the modular adder in the beginning of the reverse converter is considered as a part of reverse converter instead of a part of arithmetic unit.

There are two common adders in computer arithmetic [1]: carry-propagate adder (CPA) and carry-save adder (CSA). The CSA has three input operands while CPA has two operands. Besides, CSA is faster and simpler than CPA adder that uses the complex parallel prefix structure to increase the speed. The issue of parallel prefix for increasing the speed has become more serious when it comes about the modular adder. However, CSA generates redundant output in the form of carry and sum binary vectors. It should be mentioned that the proposed technique can be only applied on the reverse converters that uses the new CRT-II [2] formula since only in this type of formula the modulo of adder in input of the converter can be the same as the modulo of one of the arithmetic unit modulus.

The main idea of this paper is that in RNS system for some modulus, if the modulo of the final modular adder of the arithmetic unit is the same as the modulo of modular adder that is in the beginning of the reverse converter, this adder can be eliminated and then the Carry and Sum signals are entered to the reverse converter where they are added by an extra CSA that is placed to converter. To explain the proposed method, the main formulas of [4] can be written as follows:

X = Z+2ⁿ(2²ⁿ⁺¹ — 1) 12^й (К — Z)|₂2„_₁ ; (1)

Z = x₁+2ⁿ|2ⁿ (%₂ - x₁)|₂2h₊i_i ;     (2)

У = %3+(2n + l)^"1 (%4 - x3)|2"-i - (3)

Where %i, x2, хз andx4 are four residues in the moduli of 2n, 22n+1 - 1, 2n + 1, and 2” - 1 ,respectively. However, in a full RNS system these residues are resulted from a modular multiplication or addition operation where each of them has a modular adder as the final adder. For example, x2 can be written as:

^X2 ⁼ l^S2 + ^c2U²ⁿ⁺¹-l"           (4)

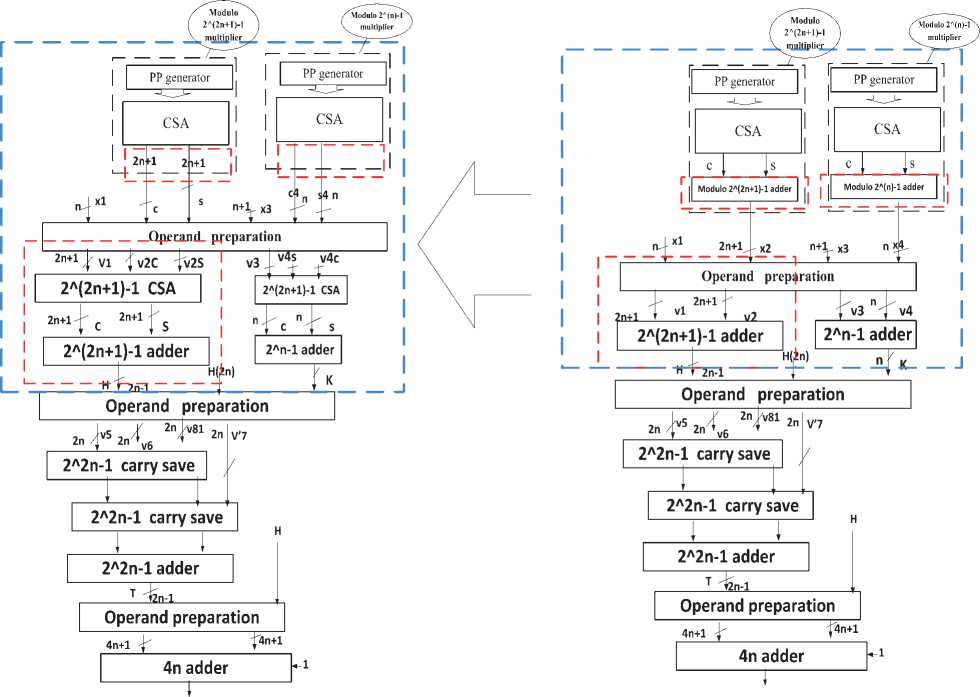
Fig. 1.The previous design including a maultiplier that is connected to a reverse converter in the right and, the new design that is consisted of a multiplier without the last modular adder, and a modified reverse converter in the left

Where, Si and c₂ are the redundant results of CSA addition of corresponding partial products. As it can be seen the conversion formulas in (1)-(3) are composed of two terms 2ⁿ|2ⁿ(x₂ -xJIzZn+l-! and (2ⁿ + l)|2^n-1 (x₄ - x₃)|₂"-i.. In the term 2ⁿ|2ⁿ (x₂ - х^гп+т^, the modulo of X2 is the same as the result modulo 2²ⁿ⁺¹-1.

Therefore, as described before the term ^2 can be replaced by its equivalent from (4) and instead of two cascaded modular CPA additions, a CSA and a modular CPA addition can be performed. Hence, we have:

Z = x₁+2ⁿ|2ⁿ (|s₂ + c₂\₂2n+i_₁ — ^Xl)l2²ⁿ⁺¹-1 ^—               (5)

X!+2n|2n (s2 + c2 - X2)|22n+i_1.

If the residue %4 is considered as (6), in the same way, Y can be written as (7):

X4 = |s4 + C4l2n-1 ;            (6)

У = x3 + (2n + l)|2n-1 (x4 — x3)|2n_i

— Xg + ^Z^ H~ 1)|Z^~^ (S4 + ^4 — ^з)12п 1" (7)

Where S'4 and C4 are the redundant results of a CSA. Fig.1 compares the presented method in the left with previous method in right. It can be seen in the proposed method that the modular adder in the end of multiplier is specified by a dotted rectangular shape. This adder can be eliminated as shown in Fig. 1. The outputs of these adders are x ₂ and x ₄ that are inserted to the converter, respectively. Instead of x ₂ and x ₄, the corresponding redundant CSA results ( s , c ) and ( s ₁, c ₁) are entered directly to the converter.

Performance Evaluation

The proposed and previous designs are described in VHDL codes, synthesised and optimized by Synopsys Design Compiler. The 180-nm generalpurpose standard cell library was used. Generally, the designs are divided in two groups: i) reverse converter of [4] plus modular adders in used its inputs and ii) the proposed reverse converter that eliminates the modular adder in input of reverse converts as described in before. For each group the following states were considered:

– full adder (FA) based CPAs is used in reverse converter and modular adder;

– parallel prefix based CPAs is used in reverse converter and modular adder.

Tables 1 and 2 give information about experimental results that have been achieved based on the different designs. The implementations were done for the three circuit parameters: delay, power consumption and area. It must be noted that the comparison was done between the proposed designs and [4].

Tables 3 and 4 show that the proposed method of shifting modular adder from arithmetic unit to the reverse converter results in significant improvement in delay and Energy (Power-Delay Product). For example, the speed up in the first state for n = 12 is more than 26% rather than the previous design. The proposed method has the best speed up when the FA-based CPA is used in adders. Besides, Tables 3 and 4 indicate the amount of PDP improvement of proposed customized adder plus reverse converter over previous design. For example, the PDP improvement has been about 22% for 10-bit in the state-2. Generally, two points can be extracted from experimental results:

– although, the power consumption is not improved in some cases, the gain obtained by speed up is so significant that totally makes the performance better and compensates the power consumption loss;

– the best PDP is related to the state-2 where all CPAs are parallel prefix. Therefore, the proposed method has the best PDP when parallel prefix is used.

In addition, as it was predictable, the efficiency of the proposed technique is contributed to the fact that the design area has been reduced by 13% for 12-bit in compare with the previous design for the state-1. This improvement can also be seen in all states that has been better at least more than 5%.

Table 1. Experimental results for proposed and previous design when FA-based CPAs is used in reverse converter and modular adder

n	Proposed design			Previous design
	Delay (ns)	Area (z/m2)	Power (mw)	Delay (ns)	Area (z/m2)	Power (mw)
10	8.39	28962.	23.123	10.6	30935.	21.95
12	10.1	35582.	28.667	12.8	37701.	26.10

Table 2. Experimental results for proposed and previous design when Parallel prefix based CPAs is used in reverse converter and modular adder

n	Proposed design			Previous design
	Delay (ns)	Area (um2)	Power (mw)	Delay (ns)	Area (um2)	Power (mw)
10	3.48	46283.	23.196	4.14	51469	23.127
12	3.68	57942.	28.703	4.51	61581	28.728

Table 3. The percentage of improvement (%) for proposed design over previous method for four parameters: delay, area, power consumption and PDP when FA-based CPAs is used in reverse converter and modular adder

n	Delay (%)	Area (%)	Power (%)	PDP (%)
10	25.73	5.95	-8.9438	14.49
12	26.91	6.26	-5.7	19.56

Table 4: The percentage of improvement (%) for proposed design over previous method for four parameters: delay, area, power consumption and PDP when Parallel prefix based CPAs is used in reverse converter and modular adder

n	Delay (%)	Area (%)	Power (%)	PDP (%)
10	22.55	6.28	0.0870	14.49
12	20.73	8.84	0.6149	21.47

As it can be seen the best performance for area is observed when the parallel prefix adder is used only in arithmetic unit.

Conclusion

In this paper, a new approach to design RNS systems has been introduced. This method is relied on the fact that the reverse converter design and arithmetic unit must be considered together not separately that is common in the previous methods. By taking the advantages of this view, the modular CPA of final arithmetic unit that is one of the main factors in increasing RNS overhead is replaced by a CSA. Experimental results show significant reduction in both speed and power consumption of RNS system that uses the proposed method.