A novel approach to thwart security attacks on mobile pattern authentication systems

Published Online May 2018 in MECS

In Android mobile systems, a 3x3 lattice of the pattern lock is offered to the user to select a pattern such as (1-45-6-9) as shown in fig 1, to serve as a password to access the device.

This graphical password[1] is hashed using SHA-1 and the hash code

“8cb2237d0679ca88db6464eac60da96345513964”

is stored in a file called “gesture.key” in the device folder of Android[2]. But this hash value is not safe from the attackers as users normally leave their mobiles USB enabled and rooted. If the phone is rooted or USB enabled, the attacker may utilise android forensic tools and existing SHA-1 dictionaries[3] and gets the corresponding pattern of the hash and makes a passive attack on the pattern. The SHA-1 predefined dictionaries and rainbow tables contain hash value for each combination of pattern which ranges from 1234 to 987654321. Since the number of patterns is limited in number, it is not difficult to crack or bypass the pattern.

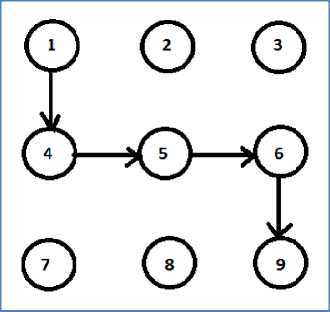
Fig.1. Pattern locks for Android

After the user selects the pattern password, device hashes it with SHA-1 hash function and saves result into the password file. At any time when the user tries to unlock the device compares the stored SHA-1 hash with newly calculated hash value to give access or not. The problem with Android pattern locks is, it stores pattern lock data as an unsalted hash value. If we select a pattern 14569, this pattern is stored with a 20-byte SHA-1 hash. So the SHA-1 hash for 14569 is

“5be3abe776eaf5f251122aba6f291eb40b65aa3d”

which is stored in a file called gesture.key in /data/system folder in Android’s internal memory of the device. Android patterns are not salted hashes. It is possible to crack SHA-1 hash in no time and reveal the original pattern using android gesture.key file. These attacks are possible when the mobiles devices are left either rooted or USB enabled. Since SHA-1 is a one-way encryption function, there is no reverse function to convert hash code to original message sequence. To restore the code, the attacker will need to generate a hash table of patterns with hashed strings. He can download the SHA-1 dictionaries[24] and without difficulty finds hash to recover the original pattern sequence. If you have full access to a mobile, you can just remove or replace the file containing the SHA-1 pattern password. An attacker uses forensic tools such as Andriller(shown in fig 2) to achieve the password using a dictionary that can be downloaded and using a forensic tool such as SqLite browser, the attacker can easily find the original pattern by running the query,

“Select * from Rainbow Table where hash = “6a062b9b3452e366407181a1bf92ea73e9ed4c48”.

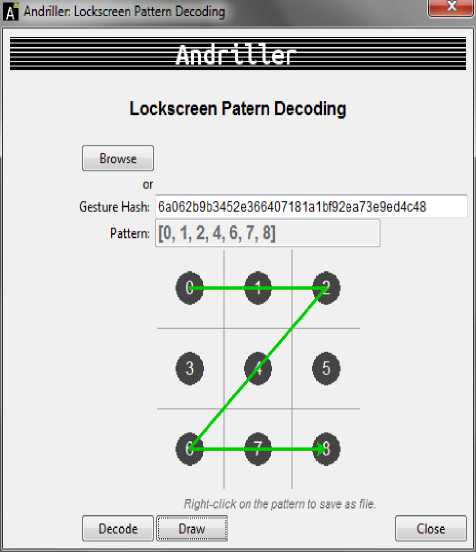
Fig.2. Android Forensic Tools that Attack Passwords

Now after gaining the password he can keep on attempting passive attack on the device. But adding a salt value to the hash solves this problem. Salts always prevent dictionary attacks. Even after using salts the security is not ensured because salts are stored in the device databases, and if salt is hacked, the attacker can exercise brute-force[21] attack using the salt value to crack the password, and such forensic tools also are available widely.

After KitKat 4.4, Android brought some changes in the authentication systems, which contain salts for hashing particularly in Lollipop and Android latest (Marshmallow) versions. But salts will not solve the problem completely because we store them in database, if compromised the attacker may brute force the password using the salt value. Once the salt is compromised, because having 100% security for any security system is not achievable, the attacker finds some way to gain the salt value and he can still try the brute force attack, to gain the password. Many researches

In this paper we focus on how to get rid of precomputations on patterns. We need to have a solution to amend pattern authentication systems so that they can withstand to dictionaries. Here we made the representation of the pattern totally different from the existing one, and it alters from user to user depending on his identities. We have incorporated the application of elliptic curves in pattern representation. In the current research, we generate a dynamic pepper values for the hash to be stored in the databases, and as the pepper is dynamic in nature, they stretch the passwords and bruteforcing becomes impossible for opponents. Obviously peppers prevent dictionaries and rainbow tables.

In this work, we generate a dynamic pepper, which if added to pattern passwords, the patterns become resistant to dictionaries and rainbow tables and brute-forcing as this value is unknown. Elliptic curve [4] based cryptosystems provide more security with less amount of memory and hardware and key sizes, when compared to other cryptographic techniques, so elliptic curve cryptosystem may be accepted for mobile devices. Genetic algorithms[5] such as mutation and crossover[6] are used to generate the pepper value, which serves as improved encoding of data for pattern password hashes.

• II.    Related Works

This research mainly concentrates on the solution to the pre-computations on the modern android pattern locks. As pattern locks are prone to dictionaries, rainbow tables and brute forcing, a more secured authentication system is needed to make them strong enough to withstand these attacks. A detailed study on the Android SHA-1 hashes, adding salts and peppers, elliptic curves and cryptography is made.

• A.    Salts and Peppers

A salt is a randomly produced value generally stored in the database and is designed to make it impossible to utilize dictionaries to crack passwords. If each password has its own salt, they must all shall be brute-forced individually to crack them. However the salt is stored in the database along with the password hash. A pepper is an unknown salt value, usually hard-coded or generated in the application's source code, which is supposed to be secret. It is used so that a compromise of the database would not reason the entire application's password table to be brute-forceable. A pepper is a secret key. It is an unknown salt and is a random salt that you are not storing in the databases. The pepper is different for each user like a salt. It is not stored at all. Peppers and salts stretch the length of the passwords and consequently improve security with regard to brute-forcing. They also save passwords from rainbow tables and dictionaries.

• B.    Elliptic Curves

Elliptical curve cryptography (ECC) is an asymmetric key encryption technique based on elliptic curves that can be used to produce faster, smaller, and efficient cryptographic keys. Secured keys created using ECC through the properties of the elliptic curve equation as a wonderful alternative of the traditional technique i.e. generating the product of very large prime numbers. The technology can be used in a combination with most public key encryption methods, such as RSA, and Diffie-Hellman Key Exchange.

According to some research ideas and researchers, ECC can provide a level of security with a 164-bit key that other systems require a 1,024-bit key to attain. Because ECC helps to set up equivalent security with lower computing power and battery resource usage, it is attracting the people widely to be best used for mobile applications.

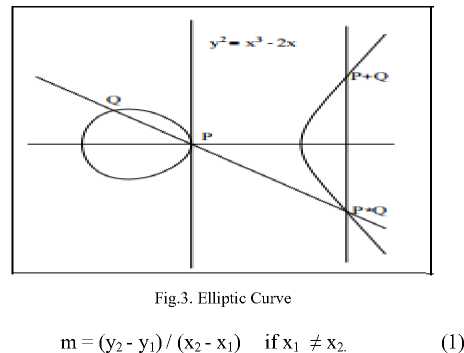
An elliptic curve is a set of points described by the equation: y² mod p=x³+ax+b mod p where 4a³+27b²≠0. The fig 3 show such a curve where a=1 and b= -2. Based on the values of a and b, elliptic curves may presume diverse shapes on the plane. A point at infinity (also known as ideal point) is a part of the curve and is denoted by the symbol 0 (zero). The points on the curve form a group with point addition. Let P(x₁, y₁) and Q(x₂, y₂) be the points on the curve and (x₃,y₃) is sum of these two points, then the formulae for point addition (P+Q) and point doubling (2P) are shown in the equations (1-4).

m = (3x12 + p)/ 2y1   if x1 = x2.(2)

x3 = m2 - x1 - x2

y3 = - (y1 + m (x3 - x1) ).(4)

Given a point P and a scalar n, computing np=P+P+…+P (n times) is called as scalar multiplication, and given points P and Q, finding n such that P=nQ is called discrete logarithm problem of elliptic curves which makes this cryptosystem strong.

• C.    Koblitz’s Encoding

The main disadvantage with elliptic curve cryptography[7] is encrypting or hashing a plaintext is difficult. The text should be encoded to points on the curve before we apply any elliptic curve based techniques on it. Koblitz[8] proposed a technique to encode a character to a point on the curve like this: a supporting base parameter, k, is selected. For a single character, m, its x value is calculated by x = mk + 1.

If there exists a matching value of y on the curve, this (x, y) point on the curve is treated as the corresponding point to represent the message character m. Else, iteratively spot the value y by changing x from [(mk) + 2] to [(mk) + (k-1)]. If substituting x = [(mk) + (k-1)] also will not solve the problem, and there exists no y value, then increment the base parameter, k, by 1 until we solve it for y. For decoding consider each point (x,y) and place m to be the greatest integer less than (x-1)/k. Then the point (x,y) translates as the symbol m. Koblitz’s technique is most efficient and very frequently used technique to map the text to points of the curve. We can directly map a character to a point on the curve as a one-to-one mapping technique, but this method is not much secured.

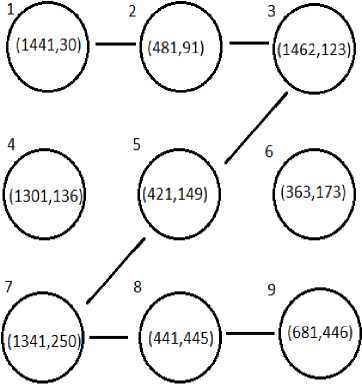
Fig.4. Representing Pattern using Elliptic Curve Points

• III.    Existing System (Salted SHA-1)

The existing system dynamically generates a salt[18] value based on user’s Device-Id and Gmail-Id. This salt is not needed to be stored in the system’s directory, and thus eliminates brute-forcing and other re-computation attacks such as dictionaries and rainbow tables as well. The salt value is distinctive to each password. So a more protected password storing technique can be achieved. A salted hash has an advantage that even though the hash is cracked you cannot get the password.

Step 1:   Represent the pattern using points on the elliptic curves shown in fig 4(the process is clearly given in the proposed system).

Step 2:    Generate an integer n by performing series of

XOR operations on the character of the Device-Id.

Step 3:    Choose a user pattern p to authenticate.

Step 4:   Now all the points on this chosen pattern are multiplied by n using Scalar Multiplication[12] giving different points on the same curve.

Step 5:   Now concatenate these points after converting them into hexadecimals to represent to a message.

Step 6:  Break this message into two halves and XOR with each other.

Step 7:   Perform step 2 twice to produce an intermediate message m.

Step 8:   To make this message a 64-bit value, reverse the two halves and concatenate them to pad the string.

Step 9:    Mark this message as a Salt value for SHA-1.

Step 10: Concatenate the salt with the original pattern selection i.e. P.

Step 11: Generate SHA-1 hash of this message.

Step 12: Store this hash value in the device root directory to authenticate the user.

Then the salt generated by using above algorithm for a pattern is 7-4-1-5-9-6-3 is ‘0260641073426714’ and finally the SHA-1 hash produced for

0260641073426714:7415963 is

• IV.    Focus of the Work

Brute-forcing is the finest password cracking methods. The success of this attack depends on several factors. However, factors that affect are password length and combination of characters. This is why forensic experts always talk about strong passwords; they generally suggest users to have longer passwords. It does not make brute-force unfeasible but it makes brute-force more difficult and makes it needs a longer time to reach the password by brute-forcing. All hash cracking algorithms utilise the brute-force to hit and try. This attack is best when attackers try it offline.

• A. Problems with Shorter Salts

We have already seen that salts will stretch the password length and prevent dictionaries and make bruteforcing harder. If the salt is too short, an attacker can create a lookup table for every possible salt. To make it impractical for an attacker to create a lookup table for each and every possible salt, the salt must be longer. A good rule of thumb is to create a salt that is the same size as the output of the hash function. For example, the output of SHA-1 is 160 bits, so the salt should be at least 20 random bytes. Moreover, there are many popular tools for brute-forcing are available in the market

GPU (Graphical Processing Units) can be best used in brute force attacks. GPUs are very good in performing parallelising mathematical operations, which is the basis of both cryptography and computer graphics. As GPUs perform massively parallel computations, they are good for brute-force attacks. Therefore our motivation in this paper by modifying the current system is to generate a pepper or a longer salt so that brute-forcing attack may become more and harder for the cryptanalyst to crack the passwords. The current system shows a better improvement regarding brute-force security for pattern passwords as compared to the existing system.

• V.    Proposed System

The proposed algorithm Peppered SHA-1) is different from existing algorithm by generating a pepper values to be prepended or appended to the pattern password[9] to generate a hash. This process utilises elliptic curves[10] to generate the grid and to represent the grid points. The steps of this algorithm are described below with the help of a flowchart in figure 5.

Step 1:   Select Android-Id and Gmail-Id of the user.

For example, Device-Id =  "67fda43cc1010bca",

Step 2:   Concatenate the user’s Gmail-Id and Android-

Id giving a long string STR.

In the current example, it is

Step 3:   Now select elliptic curve parameters to generate the grid.

Let’s suppose a= 9; b=7; p=2011;

The elliptic curve equation is y2 (mod 2011) = x3+9x + 7 (mod 2011).     (5)

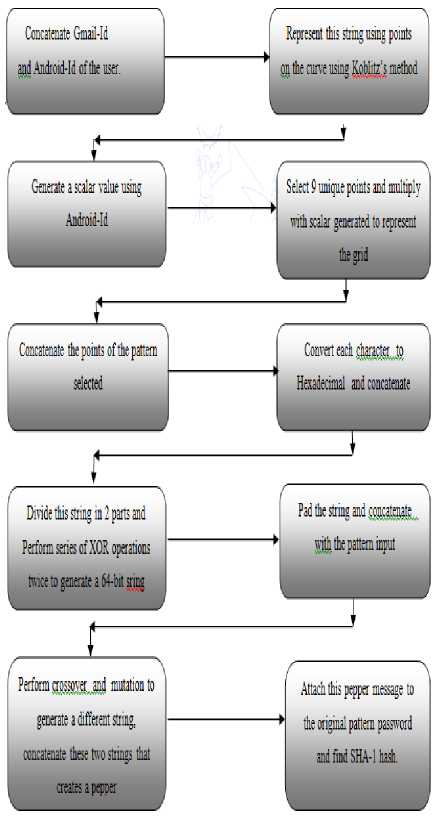
Fig.5. Flowchart of Salt and Pepper Dynamic Generation Scheme

points. So, we get (1741,16) (1441,30) (481,91) (1462,123) (421,149) (363,173) (1721,195)

(1341,250) (441,445)

Step 6:   Now the pattern grid is represented using the selected points. Let us say, points and the pattern selected by user is “123569” which shown in fig 6.

Step 7:   Now select the points for the input pattern

‘12345’. We get the points  (1741,16),

(1441,30),  (481,91),  (421,149),  (363,173),

(441,445) to represent the pattern “123569”.

Step 8:   Now derive an integer value from the Device-

Id by performing a series of Exclusive-OR operations after converting each character to corresponding ASCII value We get 54 ⊕ 55 ⊕ 102 ⊕ 100 ⊕ 97 ⊕ 52 ⊕ 51 ⊕ 99 ⊕ 99 ⊕ 49 ⊕ 48 ⊕ 49 ⊕ 48 ⊕ 98 ⊕ 99 ⊕ 97 = 5.

Step 9:   Now perform a scalar multiplication of the selected pattern points with the integer derived using Device-Id. We get different points on the curve to represent the pattern password. Here by performing the following scalar multiplication[11] operations.

5(1741,16) = (1349,1265)

5(1441,30) = (1792,1884)

5(481,91) = (1217,1022)

5(421,149) = (1171,281)

5(363,173) = (1671,1250)

5(441,445) = (457,931)

Step 4:   Now represent all the characters in the above string STR, with a point on the curve of equation(5) using Koblitz’s Encoding.

Table 1. Representation of Characters of the String using Elliptic Curve Points

6 → (481,91)	7 → (502,661)	f → 1441,30)
d → (1401,672)	a → (1341,250)	4 → (441,445)
3 → (429,149)	c → (1382,758)	c → (1382,758)
1 → (381,554)	0 → (363,173)	1 → (381,554)
0 → (381,554)	b → (363,173)	c → (1382,758)
a → (1341,250)	a → (1341,250)	c → (1382,758)
c → (1382,758)	o → (1624,862)	u → (1741,16)
n → (1603,905)	t → (1721,195)	n → (1603,905)
a → (1341,250)	m → (1587,865)	e → (1421,830)
@ → (681,446)	g → (1462,123)	m → (1587,865)
a → (1341,250)	i → (1502,557)	l → (1561,975)
. → (321,525)	c → (1382,758)	o → (1624,862)
m → (1587,865)

Step 5:   Randomly select 9 unique points from the above using any criteria. Here we sorted the points in ascending order according to y-coordinate and selected the first 9 unique

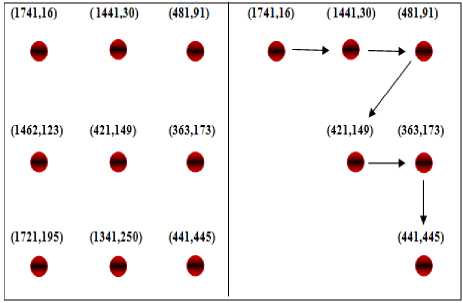
Fig.6. Pattern representation of 1-2-3-5-6-9

Step 10: Represent the pattern input using the points we have got after scalar multiplication and concatenate them after converting to hexadecimal. So the hexadecimal points (545,4F1), (700,75C), (4C1,3FE), (493,119), (687,4E2), (1C9,3A3) are concatenated and produce a string:

‘5454F170075C4C13FE4931196874E21C93A3’.

Step 11: Now break this string into 2 halves and perform Exclusive-OR operation with each other. and repeat this twice to finally get a string.

5454F170075C4C13FE ⊕ 4931196874E21C93A3 = 1D65778187370715080776.

The above string is again divided into two halves: (pad with 1’s if string length is odd)

1D657781873 ⊕ 0715080776 = 674142701F05.

Step 12: To make this string a 64-bit value, we need to pad this string. For that we break the string into 2 halves, reverse them separately, we get 241476, 50F107. By concatenating these two strings, we get 24147650F107. Add this string to the string derived in Step 11, and take the first 16 bits to represent the final dynamic message. After choosing the first 16-bits of 674142701F0524147650F107, we get String-1 = “674142701F052414”.

Step 13: Generate a second dynamic message string applying genetic crossover and mutation [12] on the string we have got in Step 12. The string we      got      in      Step      12      is

‘674142701F0524147650F107’. Now make this string into 2 halves and perform 1-point crossover.

Crossover:

Perform 1-point crossover:

701F05                          674142

50F107                        241476

The string we get after crossover   is->

67414250F107701F05241476.

Complementary Mutation:

Perform complementary mutation[13] by converting this string to binary and invert them for complementary mutation and again convert the binary string to hexa decimal we get a string,

‘98BEBDAFCEF88FECFADBEB89’.

Now take the 16-bit bit pepper from the above string as “98BEBDAFCEF88FEC”.

So String-2 = “98BEBDAFCEF88FEC”.

Step 14: Now concatenate the above two strings to generate a dynamic pepper of 128-bits.

Step 15: Pepper = String-1 + String 2

= “674142701F052414 98BEBDAFCEF88FEC “

“674142701F05241498BEBDAFCEF88FEC:123569“ is

“D109611DC681E8CB393E31EE0804246172429C2F”, is stored in device database. This salt and pepper always prevent the pattern passwords[14] from pre-computations such as dictionaries, rainbow tables and brute-forcing.

• VI.    Brute-force Security Analysis

In this paper, we are presenting a scheme for pattern passwords to prevent dictionary attacks and brute-forcing. Assailants can extract the hash value from the device database and experiment offline brute-force attack to guess the pattern. But here a pepper is dynamically generated and this dynamic pepper (long salt) of 128-bits makes the system stronger to withstand to precomputations. Here we can see the effect of prepending the pepper value as they increase the brute-force search space and consequently increases the effort needed by the attackers to crack the passwords compared to the existing method i.e. Salted SHA-1. There are nearly 4 lakhs combinations for the pattern locks which can be selected by users.

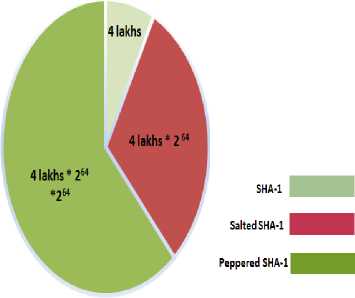
Fig.7. Brute-force Search Space Comparison of the Current System and Proposed System

As we can observe in the above graph in fig 7, the brute-force search space for the proposed scheme is increased by 264 times that of the existing system. This shows the proposed enhances security with respect to brute-forcing.

• VII.    Experimental Results and Performance Evaluation

The performance the proposed scheme i.e. pattern authentication[15] using Peppered-SHA-1 can be estimated using any criteria of hash[17] algorithms like collisions and hashing time and avalanche effect. Here as it is not practical to estimate the number of collisions of the proposed scheme as they are nearly 4 lakhs of combinations of pattern passwords for a 3X3 grid. So, we have tested the performance of the system with respect to time complexities and avalanche effect and search space for brute-forcing. Avalanche Criterion in cryptography refers to one of the significant properties of cryptographic hash functions. The avalanche effect is fulfilled if, the output changes considerably as a result of a slight change in input. Here the experimental results and comparison of the existing system and proposed system for pattern passwords is presented.

• A.    Strict Avalanche Effect

Strict avalanche Effect is a formalization of the avalanche effect The Strict Avalanche Criterion (SAC) is a property that satisfies the following criteria of the hash functions[16], “if, whenever a single input bit is complemented, every output bit should change with a probability of one half.” SHA-1[23] exhibits Strict Avalanche Criterion. Here, as the input of the pattern is and peppered, after the modifying the initial input data for hashing, we can test the diversions in avalanche effect of the current scheme. We have tested the SAC for the existing systems SHA-1, Salted SHA-1, and the proposed scheme Peppered SHA-1 on a computer with 4GB RAM, i3 Intel core processor, 1.90 GHz processor and a 64-bit OS. We have taken the results and calculated the SAC for these schemes, by taking 100 pairs of input plaintext messages.

We have observed the Avalanche Effect by collecting casual input pattern pairs of 4-point, 5-point, 6-point, 7-point and 8-point patterns respectively, where the inputs vary in one single bit. We have plotted the graphs for all the above combinations of patterns to observe the avalanche criterion of the proposed system and current system.

The following figures 8-12 show the SAC between the proposed and current schemes. We took the pattern number on x-axis and Avalanche Effect of that input pattern on y-axis.

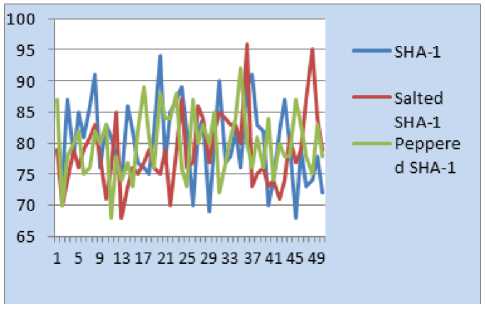
Fig.8. 4-point Pattern SAC

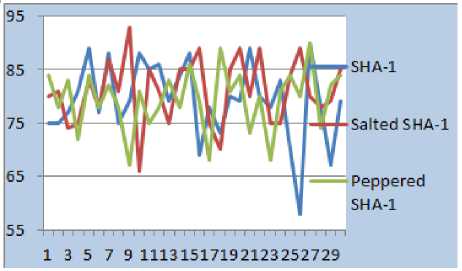
Fig.9. 5-point Pattern SAC

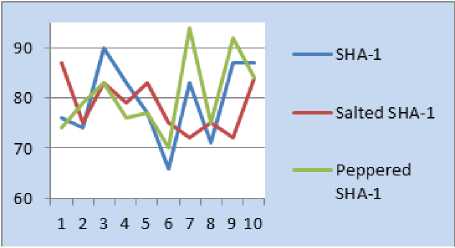
Fig.10. 6-point Pattern SAC

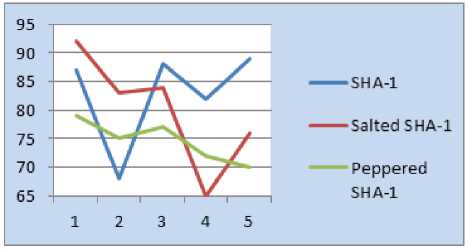
Fig.11. 7-point Pattern SAC

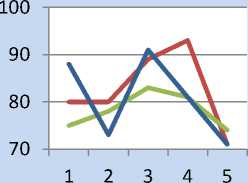
i     SHA-1

^^^^^еSalted SHA-

^^^^^^ Peppered SHA-1

Fig.12. 8-point Pattern SAC

Table 2. Average SAC Statistics of Different Patterns

SAC	4-dot	5-dot	6-dot	7-dot	8-dot	AVG
SHA-1	50.18	49.5	49.6	51.75	51.6	50.52
Salted SHA-1	49.2	50.64	49.06	50	48.87	49.55
Peppered SHA-1	49.95	49.66	50.25	46.6	50.5	49.39

The results prove that the time complexities are getting increased more than twice that of the current system as shown in table 2. These observations are taken with a computer system with 4GB RAM, i3 Intel core processor, 1.90 GHz processor and a 64-bit Operating System. The above graphs reveal the performance of the proposed scheme with respect to SAC as compared to SHA-1 and the Salted SHA-1 schemes, for various sizes of the pattern. We can also observe the overall SAC for various pattern sizes as given in the table-2 and figure 13.

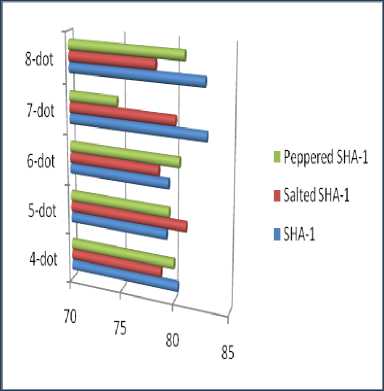
Fig.13. Average SAC of the 3 Methods

Figure 13 shows the presentation of Strict Avalanche Effect of the three methods. From the results obtained, we can deduce that the proposed method i.e. Peppered SHA-1 exhibits the SAC irrespective of the pattern sizes as like SHA-1 and Salted-SHA-1.

• B.    Time Complexities

The time complexity of an algorithm measures the amount of time taken by an algorithm to run as a function of the size of the input. We always need efficient algorithms as processor time is expensive. Computation has no use if it takes exceedingly long time to solve a problem.

But slow hash functions do have some advantages if they run in less amount of time. Brute-forcing consumes much time for slow hash functions. So we have calculated the time complexity of the proposed algorithm to test the performance. Figures 14 and table 3 show the average running times for the hash generation of the current and proposed systems for various pattern sizes after results are observed after execution.

Table 3. Average Execution Times of the 3 Methods

CPU Time in millisecs	4-dot	5-dot	6-dot	7-dot	8-dot
SHA-1	8	7.5	8	8	7.5
Salted SHA-1	21	21	21	24	23.5
Peppered SHA-1	24	23.5	24	23.5	23.5

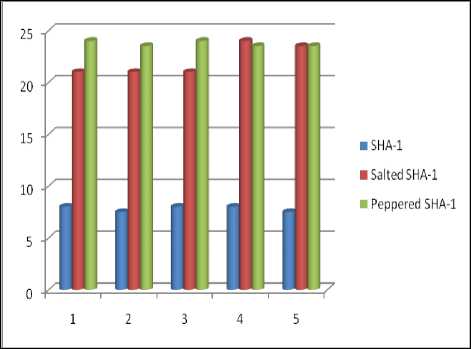
Fig.14. Average Execution Times in Milliseconds

We can observe from the above graph that the time complexity of the proposed system is increased as this scheme is an extension of the SHA-1 algorithm. The results prove that the time complexities are getting increased more than twice that of the original system i.e SHA-1. But there is no much difference between the CPU times of the salted SHA-1 and peppered SHa-1 systems. These observations are taken with a computer system with 4GB RAM, i3 Intel core processor, 1.90 GHz processor and a 64-bit Operating System. Here the scalar multiplication algorithm, crossover and mutation algorithms take additional amount of CPU time. There are always security and time efficiency trade-offs for any cryptography algorithm, but here we provided security to the existing hash generation system of pattern authentication[22] schemes at the cost of increasing the time complexity for generating the hash value. However a slow hash functions increases security against bruteforcing.

• VIII. Concluson

Security and usability are treated as the most important factors of the system design that augment the user responsiveness of the system. Android mobile requires high user friendliness. Because of several attacks on android mobiles have increased in present times, highly sheltered authentication techniques have become essential. There is no much difficulty in hacking or bypassing the pattern authentication schemes for Android mobile users, the only real obstacle is that we can make it not practical to directly access the “ /data/system/ folder “ and gesture.key file except when we are dealing with a USB enabled or a rooted device. We need new security approaches that keep away from undesired taps on the mobiles and presents better authorization schemes than the existing one with respect to rainbow and dictionary attacks. Further security enhancement of these security schemes is very much crucial to withstand to the pre-computation security threats. When hashing passwords, the two most momentous considerations are the computational cost and security measure. The more computationally costly the hashing algorithms, the longer it will take to brute- force its value. We already knew that there is a salted SHA-1 scheme that generates a dynamic salt value to prevent these attacks. But still we need to improve the salt sizes so that brute-forcing becomes much more difficult. In this work we have improved the existing salted SHA-1 method and enhanced this scheme to generate a dynamic longer salt or a pepper that can be attached to the original passwords to become strong against pre-computation attacks. As the grid is dynamically generated using elliptic curve points based on user identities such as Device-Id and Gmail-Id, passwords and hashes become unique for each user.

Here we introduced a dynamic genetic pepper value for mobile pattern authentication systems based on Genetic Algorithms, as GA can keep the strength of the algorithm and serves as second level protection. The present study introduces a dynamic pepper generation algorithm that generates a hash which is unique to the user, because it is designed based on user’s identities for Android[19] patterns systems. We proposed a modified approach to generate the salt and pepper for SHA-1 hashes based on elliptic curves[25]. This improves the strength of this algorithm as elliptic curve discrete logarithms make the system strong and secured.

The pepper is dynamically generated, it is not subjected to brute-forcing using dictionaries. As peppers are prepended to passwords, the dictionary and rainbow table attacks are not possible as well. As pepper is added to passwords which are longer than salt and stretched the password length, the scheme becomes more tolerant to brute-forcing. So this algorithm enhances the quality, efficiency and effectiveness of the existing technique being used for the pattern passwords.

With the experimental results, it proves that the existing system follows Strict Avalanche Criterion (SAC), and time complexities of the proposed technique show that the new algorithm that generates pepper dynamically involves more time because it is an extension of the original algorithm. The proposed scheme is more secured because it involves elliptic curve arithmetic and discrete logarithms[20].