A Novel GAN-based Chaotic Method with DNA Computing for Enhancing Security of Medical Images

Nowadays, the uses of medical images for the treatment of patients and diagnosis purposes are very important. Medical image analysis is essential for quick and accurate diagnosis and treatment. The medical imaging modalities, namely ultrasound, Magnetic Resonance Imaging (MRI), X-ray, and Computed Tomography (CT) are used in the diagnosis of patients. The size of these medical datasets is rapidly increasing day by day. Although some medical images contain private and sensitive data about patients, disclosing them could cause patient privacy issues. Therefore, many techniques for securing these images from cryptographic attacks and efficient storage have been proposed. Some of them are image watermarking [1], image steganography [2], image encryption [3], and lossless compression [4]. However, encryption techniques for securing medical images have grown popular in recent years. Encryption techniques are divided into two types, namely, stream and block ciphers. Stream ciphers are more efficient and faster than the block cipher encryption process, as stream cipher encrypts only one bit of data at a time. The purpose of a stream cipher is to produce unpredictable and random sequences of pixels [5]. In image steganography, the secret data is hidden inside some images, videos, and audio. So that it can be made invisible to attackers. However, it is different from encryption in terms of data readability.

Deep Learning (DL) and Machine Learning (ML) use neural networks for learning from datasets. Many algorithms are proposed by using DL, such as image segmentation [6], object detection [6], and fake image generation [7]. However, This work is open access and licensed under the Creative Commons CC BY 4.0 License. Volume 16 (2024), Issue 6

there are also many image encryption models proposed based on DL. Moreover, different sequences are produced by chaotic maps and then employed in the diffusion and confusion processes of cryptography. The chaotic map is a mathematical function that is subsequently used for generating sequences. It is highly dependent upon the number of spatial dimensions, spatial fields, and temporal fields, there are several types of chaotic maps that may be created. Various chaotic maps are subsequently used in key generation and encryption processes. Some of the most frequently used chaotic maps are the tent, logistic, Hénon, sine maps etc. Among all the above techniques, the most popular one is the encryption algorithm. In an encryption system, the data is transformed into some unreadable or irrelevant stuff, then transferred over the internet to the receiving side. To decrypt it, the receiver needs the same private key that is used at encryption time. A GAN-based key generation technique, with XOR-based encryption of medical images, has been proposed by [5]. However, there has been no discussion of compression techniques in this paper. An Artificial Neural Network (ANN) and Piecewise Linear Chaotic Map (PWLCM) for crypto-compression of bio-medical images have been proposed by [8]. This technique, however, failed to reduce the time it took to encrypt and compress data. Belazi et al. [9] have presented a chaos-based DNA encryption method for medical images. However, this algorithm just has not addressed the issue of medical imaging storage size. A new algorithm, based on improved Advanced Encryption Standard (AES) and a chaotic sequence, has been proposed to encrypt the image in [10]. In this scheme, Arnold's chaotic sequence has been used to generate a private key. This algorithm is still to be tested on medical image datasets. A new algorithm has been proposed based on a deep feed-forward ANN with Levenshtein entropy encoding for encryption and compression of medical images in [11]. The algorithm has not been evaluated on statistical analysis, that is histogram analysis, similarity analysis, and key sensitivity. Image compression and encryption using back-propagation and chaotic systems have been proposed in [12]. However, the algorithm has not been tested on medical image datasets. A new algorithm for lossless compression with the use of the Chinese remainder theorem and a chaotic approach is proposed by Brindha et al. [13]. So, the traditional approaches have several disadvantages, including ineffective encryption with compression, high algorithm complexity, high time complexity, and a lack of proper evaluation of several security metrics.

To handle the drawbacks of the current algorithms, a novel encryption and compression algorithm has been proposed in this paper. In this paper, initially, keys are generated using GAN and chaos. Then, the key's security is further enhanced using a 2D-CTM and DNA sequences. After key generation, MT and XOR-based algorithms are applied to original medical images to encrypt them. The main contribution of the proposed algorithm is as follows:

• •    We proposed a novel GAN-based 2D-CTM method with DNA computing approach for enhancing security in medical images.

• •    The 2D-CTM approach is used for improving the key generation process while deep learning-based GAN is suggested to produce keys for the diffusion and confusion process.

• •    Moreover, these medical images are encrypted by DNA encoding-based diffusion, and MT-based confusion method is used for securing purposes.

• •    Extensive results analysis is carried out utilizing metrics such as entropy, MS-SSIM, UACI, SSIM, key space, NPCR, and correlation on COVIDx-19 X-ray images, brain MRI images, and malaria microscopic images datasets.

2.    Related Works 3.    Proposed Methodology

• 3.1.    Dataset Details

  This paper makes use of a publicly accessible dataset namely, the COVIDx-19 X-ray dataset, brain MRI dataset, and malaria microscopic images dataset, respectively. All three datasets are from Kaggle. The COVIDx-19 is provided by the SIRM Italian Society of Medical and Interventional Radiology [25]. The dataset contains 9347 total number of chest X-ray images. Second, the brain tumor dataset [26]. Additionally, this brain tumor database includes meningioma, glioma, and pituitary tumor types samples with the tumor corresponding mask samples. The images are 256 x 256 resolution. Third, the National Library of Medicine malaria dataset [27] is used in the proposed scheme. The malaria dataset contains 27,558 total number of cell images with uninfected and parasitized cells. The resolutions of images are 299 x 299.

There are five sections in this paper. The discussion of related works is in the next section. The methodology part is included in section 3. In section 4, the performance of the proposed methodology is examined and evaluated with that of other existing models. Section 5 provides the paper final conclusion and future work.

The DeepKeyGen model has been proposed as a DL-based encryption and decryption mechanism for medical images [5]. The authors have used a GAN model to generate the key of the desired pattern. Then they performed stream cipherbased encryption to get cipher medical images. A detailed performance evaluation has been performed on different security metrics. However, compression has not been performed to lower the cost of storage. Mohammed et al. [8] have suggested a crypto-compression with the help of PWLCM and ANN for medical images. The results have been successfully tested on different security metrics. However, the algorithm has failed to minimize the execution time of encryption and compression for medical image schemes. Xiaolin et al. [14] have proposed an algorithm for images in RGB format. The authors have used tent maps and rectangular transforms. The algorithm encrypts all the channels of a color image simultaneously. However, the algorithm is not assessed based on medical images.

Wang et al. [15] have suggested a new encryption method based on Convolutional Neural Network (CNN) and chaotic maps. The original image is segmented in this paper, then the 4D-hyperchaotic map is generated by CNN to get a chaotic sequence. Wu et al. [16] have suggested a chaotic map with DNA-based image encryption. The author has proposed a new 2D-Hénon Sine map for the key generation process. Then, DNA-based encoding and diffusion are applied. Akkasaligar et al. [17] have suggested a new lightweight medical image encryption technique due to DNA-based computing and hyper chaos. Here, a few pixels are selected and DNA based confusion is performed and the remaining pixels are encoded into the DNA sequence. Then merge back all the pixels to get cipher image. However, the method is not evaluated in the case of noise attacks. Hosney et al. [18] have suggested a new scheme used for colored image encryption on confusion and diffusion process. A private key is generated by using a 1D-logistic map and perform the diffusion process on the shuffled image to get the final cipher image. Kumar et al. [19] have suggested a chaos-based substitution process to obtain a secure image. The substitution process is based on zig-zag scan. The 1D-logistic map is used for key generation in encryption process. Jeevitha and Prabha [20] proposed a DWT and edge map-based encryption of medical images. Here, the medical image is initially divided up into several DWT planes. Then an edge map is applied, followed by DWT-bit level permutation, to get the encrypted image. Literature survey shown in Table 1.

Table 1. Literature survey

Ref.	Objective	Modality	Datasets	Techniques
[5]	Privacy in medical image	X-ray, MRI	Ultrasound and BraTS18	DeepKeyGen
[15]	Encrypt the image	MRI, JPG	Brain, Lena	V-net, CNN, Chaotic
[17]	Perform security in medical image	CT, MRI, Ultrasound, X-ray, ECG	Chest, Brain	DNA, SDMIE
[18]	Encryption of color image	JPG	Color image	Chaos and block scrambling
[19]	Encryption/ Decryption of image dataset	JPG	Color, gray image	Chaotic convolutional and thorp shuffle
[20]	Improve privacy to medical image	MRI, X-ray, Ultrasound	Brain, X-ray, Ultrasound	Edge map and DWT scrambling
[21]	Provide security to the medical image	MRI, CT, X-ray, ECG, Ultrasound	Chest, Ultrasound, ECG	WBAN
[22]	Security and privacy to telemedicine and healthcare	CT, X-ray	Brain, X-ray	DNA chaos cryptosystem
[23]	Encryption/Decryption of medical image	MRI, CT	Dicom	Chaos-DNA-IWT
[24]	Encryption/Decryption of medical image	MRI	Brain	DNA and chaotic map

Medical imaging is distributed through the internet for use in research and patient care. However, it is crucial to protect it from attackers and preserve its integrity. In order to protect medical images before sending them over the internet, efficient encryption must be applied. A new key generation system based on GAN, 2D-CTM, DNA, chaos, and MT encryption and decryption methods is being developed to effectively protect medical images. Table 2 lists the notations used in this investigation along with their descriptions.

Table 2. Symbols along with their descriptions

Symbol	Description
X1, Y1, X2, Y2	Sequence generating using 2D-CTM
R 1	(Key[im]%8) +1
R 2	(im %8) + 1
DNA R1	Pixel encode with rule R1
Decode R1	Decode DNA with rule R1
Sin ()	Trigonometric sine function
m	Initial parameter for 2D-CTM

• 3.2.    Key Generation

The proposed algorithms initial step is to generate a strong encryption key. The proposed method uses the GAN and 2D-CTM, MT, input image, and DNA to generate a key stream having a key value encoded in DNA sequences. To begin, generate the key using GAN with the fake-image dataset. The key is generated using GAN along with a 2D-CTM. The complete flow of the key generation server is given in Fig. 1. The most important phase in obtaining a safe encrypted representation of the original image is key generation. This method creates a novel 2D-based chaotic map is produce a key stream. The equation below gives the 2D-CTM in Eq. (1).

q_n+ j = k + q_n * tan ( n ) mod 1

p_n = k + n * (1 - q_{n + 1} * tan ( n )) mod 1

where n, p n , and k is the initial value of a control parameter. To obtain the initial sequence, the equation above determines initial value for k, p n , and m. Two sequences, X1 and Y1, are produced using this map. In this method, the process of diffusion is represented by the X1, while the process of confusion is represented by the Y1. Algorithm 1 shows the algorithmic processes for key generation.

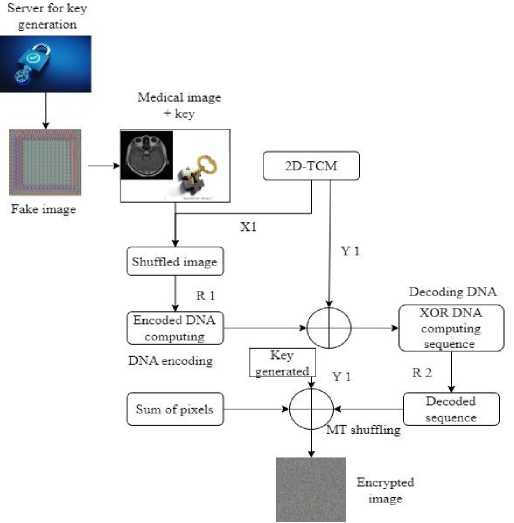
Fig.1. Proposed encryption methodology

Algorithm 1: 2D-CTM with GAN-based key generation process.

• k, n, and s are the primary parameter control. Then, generate key size ^{npu s:}       sequence as a parameter.

• 3.3.    Encryption

Output:          Secret keys sequences, Y1 and X1 keys of a (256 x 256 x 3) size

Function GenerateaKey(Mimg):

X1 ← make an empty array the default for sequence1 key

Y1 ← make an empty array the default for sequence2 key for img in range (size i ) do k = n + ((k) * tan(s)) %1

The encryption image is created from its initial form via last phase of encryption. Thus, encryption takes place based on the private key being generated successfully. The original image is first shuffled at the pixel level using the Y1 sequence produced by 2D-CTM in Eq. (2).

^ image\ y^1[^\^]   OriginCll imageU]                                      (2)

where S image denotes modified image, Original image is the initial input image, and i is index value. After receiving a shuffled image, use R1 to encode a image pixels into DNA sequence shown in Table 3. Additionally, include the key X1 value in the DNA sequence, where im £ privatekey and integer of encrypted key.

R1 ь (Key[im]%8) + 1

R2 ь (im%8) + 1

Table 3. DNA sequence-based rule for encoding and decoding

DNA base rules	Rule-1	Rule-2	Rule-3	Rule-4	Rule-5	Rule-6	Rule-7	Rule-8
T	11	11	10	10	01	01	11	00
A	00	00	01	01	10	10	11	11
G	01	10	00	11	00	11	01	10
C	10	01	11	00	11	00	10	01

After changing the values of keys and images to the DNA sequences, then performs XOR operation based on DNA to get the diffused image. Now, diffusion process is complete, it decodes a DNA sequence once again into integer values. After that perform the MT-based cipher image confusion. The total of original image's pixels, X1, and cipher image are then combined using the XOR technique to create a highly secure final encrypted image shown in Table 4.

Algorithm 2: Medical mage Encryption.

Medical image M img , where img = 1,2,…,n. The key Y1, X1 along with keys DNA encoded values, Y 1 , X 1 = 2D-CTM(), R 2 ← (im% 8) + 1,

Inputs:

sequence 2 = Mersenne_Twister(), sum ← sum of original image pixels,

R 1 ← (Key[im] %8) +1, DNAR i ← Encode pixel with rule Ri, Decode Ri ← Decode DNA with rule Ri size = M × N, X1 DNA ← encode DNA based form key X1

Output:

Encrypted images Cimg, where img = 1,2,…n while im from 0 to sizei do

S image [Y 1 [i] – 1] = M img [j] im = im +1;

end while im from 0 to sizei do

Encoded_dna[im] = DNA R1

im = im +1;

end while im from 0 to sizei do

Encoded_dna[im] = Encoded_dna[im] XOR X1 DNA [im] im = im + 1;

end for p in EncodedDNA do

Enc DNA = Decode R2

end for jm from 0 to sizei do

Encryption_image[sequence2[jm] -1] = EncDNA[jm] end while jm in range (M × N) do

Cipher image [jm] = Cipher₁ mage [jm] ф [X 1 ] ф [sum (%256)]

jm = jm+1;

end

Return C img

Table 4. XOR rule operation of DNA sequence

XOR	A	T	C	G
T	T	A	G	C
C	C	G	A	T
A	A	T	C	G
G	G	C	T	A

• 3.4.    Decryption

4.    Results and Discussion

• 4.1.    Experimental Setup

• 4.2.    2D-Chaotic Tent Map (2D-CTM)

The original is restored from its encrypted state, the encryption process must be reversed. First, the pixels are rearranged using the Y1 sequence. The pixels are then encoded using DNA. The X1 key is used to carry out the DNA-based XOR operation. Decode the image's pixels next to turn them into numbers. Reshuffle now using the MT-based pattern that was applied during encryption. Finally, to restore the original image, use an operation XOR-based between image, X1, and original image's pixel total.

The proposed novel biomedical imaging encryption methods are based on GAN, MT, DNA computing, and chaos. A DNA-based procedure is used for obtaining the final encrypted image after key generation using the 2D-CTM and GAN. Several security evaluation criteria are used to completely assess the performance of the suggested model.

The proposed model is implemented and evaluated on an Intel Core (TM) i5 processor running at 2.5 GHz, with 8 GB of RAM and 4 GB of Nvidia graphics memory (Graphics Processing Unit (GPU) [6]).

The 2D- CTM is performed by using a Sine map [28]. It is a chaotic 1D-map that is described by Eq. (3).

S_n+1  = <5 sin (X -$ п )

where δ∈ [0.87, 1] shows the behavior of chaos. The proposed novel 2D map based on the trigonometry tan(n), is shown by the following Eq. (1). Now, Fig. 2(a) and Fig. 2(b) show Bifurcation Diagrams (BD) for Sine map and 2D-CTM. The suggested 2D-CTM has no regularity in comparison to Sine map. As a result, 2D-CTM is also quite sensitive to the starting parameters. Now that Lyapunov Exponent (LE) for the 2D-CTM has been determined, it is displayed in Fig. 2 (c).

The 2D-CTM LE is positive and has positive value slightly above 0. Also, a positive LE indicates that map is currently chaotic. As a result, the suggested map exhibits a wide variety of chaotic behavior between 0 and. As a result, the sequence produced by 2D-CTM exhibits more erratic behavior. It is therefore ideal for use in the key generation process.

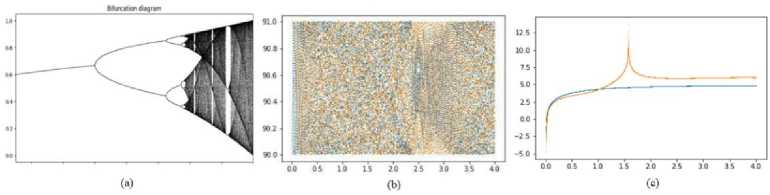
Fig.2. (a) BD Sine map, (b) BD 2D-CTM, and (c) LE of 2D-CTM [0,4] range

• 4.3.    Key Space

  The overall size of the key used for encryption is referred to as key space. It establishes how restless the model is in response to attacks involving exhaustive searches. The starting parameters k, p n , and m in the process of key generation based on 2D-CTM have an accuracy of at least 2¹⁴. As a consequence, the key space is (10¹⁴)³ = 10⁴², which is sufficiently vast to thwart exhaustive search assaults [28]. As a result, the key produced by the suggested model is uneasy around assaults involving thorough searches.

• 4.4.    Key Sensitivity

  The algorithm is sensitive when the key value is slightly altered, as seen by the key sensitivity. The initial critical parameters can alter very slightly without having a significant impact on the 2D-CTM. The secret key is produced with the initial value of q n = 0.93, u = 4, and k = 90 for the assessment of 2D-CTM towards key sensitivity. Additionally, the picture is encrypted. The decryption key is now created once more, with the exception of significantly changing the value of q n from 0.93 to 0.930000000000001. Now the encryption is performed using this key. Fig. 3 displays the decryption's outcome. Moreover, the decryption procedure utterly failed with a small change to the initial settings.

• 4.5.    Histogram Analysis

• 4.6.    Visual Quality Analysis (VQS)

Fig.3. (a) Original images of the brain, COVIDx, malaria, (b) encrypted image (p=0.93), (c) slight modification decrypted image

(p=0.930000000000001), and (d) decrypted image with correct p-value

The histogram of medical image describes distribution of pixels in a digital image. It displays how many pixels correspond to each color intensity value between 0 and 255. In general, a histogram that is uniform can fend against statistical attacks on an encryption method. The histogram analysis is studied using a variety of grayscale and color images. The analysis of a histogram shows frequencies of various values of pixels. If the cipher image pixel distribution is uniform, statistical cyberattacks against it can be thwarted since the attackers won't be able to identify any patterns in the image. The histograms of an original biomedical images and the associated encryption images are displayed in Fig. 4.

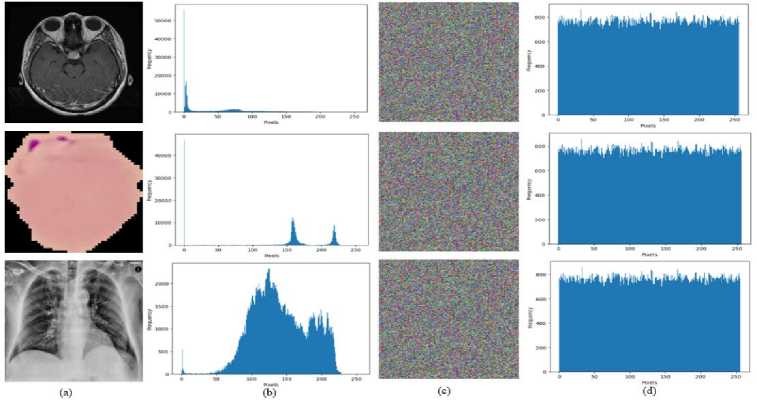
Fig.4. The histogram of an original biomedical image and its corresponding encrypted image for all three datasets

The VQS of the proposed algorithm images are measured by mean square error and peak signal-to-noise ratio.

• A. Mean Square Error (MSE)

A function of mathematical mapping termed the MSE measures the precision that an estimate performs. An arbitrary parameter is able to be mapped to a sample of values from a random vector using the MSE function. The difference between the actual and predicted images in Table 5 is strongly associated with a high MSE score. Eq. (4) provides the predictor MSE:

^MSE = мха Х^адл-пи»²

where Y(i,j) and X(i,j) represent the actual image and prediction image on the testing image of size M * N.

Table 5. Performance MSE value comparison with the existing approach

	Ding et al. [5]	Honsy et al. [18]	Proposed scheme (brain MRI image)	Proposed scheme (COVIDx-19 X-ray image)	Proposed scheme (malaria microscopic image)
MSE	11720.98	10119.53	11871.43	11892.36	11799.12

B. Peak Signal to Noise Ratio (PSNR)

The PSNR is a statistical estimate used to compare the original image's quality to an image with additional noise. The PSNR is the ratio of maximum signal power to the maximum noise power. shown in Table 6. PSNR is estimated using Eq. (5).

PSNR =20 log 10

(MAX i )

^MSE

where MAX i represents maximum pixel value of the image.

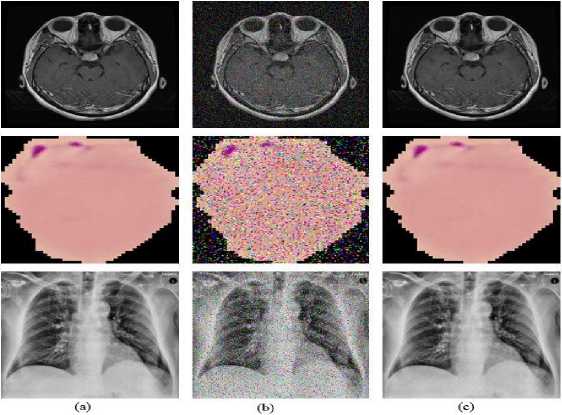
Fig.5. (a) Original image, (b) noise attack the image, and (c) denoised image

Table 6. Performance PSNR (dB) value comparison with the existing approach

	Belazi et al. [9]	Hua et al. [29]	Mishra et al. [30]	Proposed scheme (brain MRI images)	Proposed scheme (COVIDx-19 X-ray images)	Proposed scheme (malaria microscopic images)
PSNR (dB)	20.6301	8.5675	19.6340	20.82	20.97	22.32

• 4.7.    Noise Attacks

• 4.8.    Occlusion Attacks

4.9. Differential Attack

The data is sent over any communication medium. The transmission of encrypted images carries the risk of data loss. In such a case, there is a chance that the decryption process becomes invalid. These attacks are often known as occlusion attacks. So, the suggested scheme's ability to be robust to changes in the cipher image is evaluated in the robustness evaluation. As a result, the encrypted images are run through the data loss operation at rates of 1/64, 1/32, 1/8, 1/4, and 1/2 to assess the proposed model's resistance to occlusion attack. Then, the decryption procedure is performed. The MRI brain, malaria, and COVIDx-19 X-ray images in Fig. 6 show that even with a 50% decrease in data volume, the majority of the visual view is still visible after the decryption procedure.

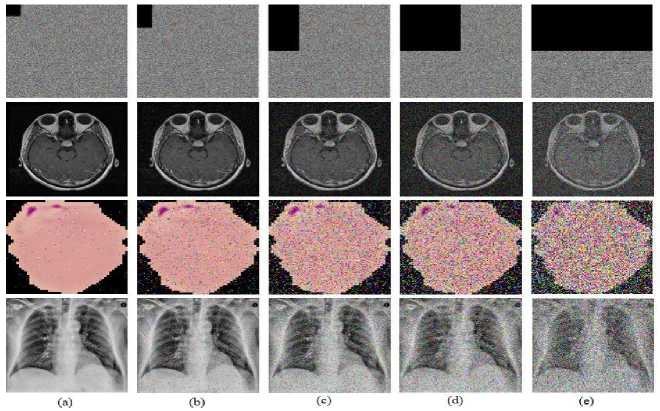
Fig.6. Visualization of the image under occlusion attack, where an encrypted image with (a) 1/64, (b) 1/32, (c) 1/8, (d) 1/4, (e) 1/2 data losses and corresponding decrypted image with respect to 1/64, 1/32, 1/8, 1/4, and 1/2 data losses and respective loss in brain MRI, COVIDx-19 X-ray images, and malaria images.

The Number of Pixel Change Rate (NPCR) and Unified Average Changing Intensity (UACI) scores are commonly used to measure resistance to differential assault [28]. The two scores show how sensitive the cipher picture is to even the slightest alteration of the associated plain image. The encryption method's sensitivity to plain picture increases with score presented in Tables 7 and 8, respectively. NPCR should be 1 and UACI should be 0.334, shown in Eq. (6), and (7).

NPCR = kli:^ * 100 m*n

UACI =

5^^100

255* m*n

Table 7. Performance NPCR value comparison with the existing approach

	Belazi et al. [9]	Hua et al. [29]	Dagadu et al. [31]	Dridi et al. [32]	Proposed scheme (brain MRI images)	Proposed scheme (COVIDx-19 X-ray images)	Proposed scheme (malaria microscopic images)
NPCR	99.53	99.59	99.62	99.51	99.96	99.66	99.43

Table 8. Performance UACI value comparison with the existing approach

	Belazi et al. [9]	Hua et al. [29]	Dagadu et al. [31]	Dridi et al. [32]	Proposed scheme (brain MRI images)	Proposed scheme (COVIDx-19 X-ray images)	Proposed scheme (malaria microscopic images)
UACI	33.48	34.26	33.53	33.42	37.36	31.73	33.62

4.10. Entropy

The Information Entropy (IE) calculates how random the encryption image is used to compute it Eq. (8). Entropy should have a value of eight. The entropy score for the medical image encryption images is determined to be 7.99913, which is extremely close to the ideal number. The suggested scheme's information entropy analysis in comparison to other approaches is shown in Table 9.

L(x) = T^iP (xl)log2p(xl)

where L(x) is IE, and p(x i ) is the pixel probability of x i image.

C

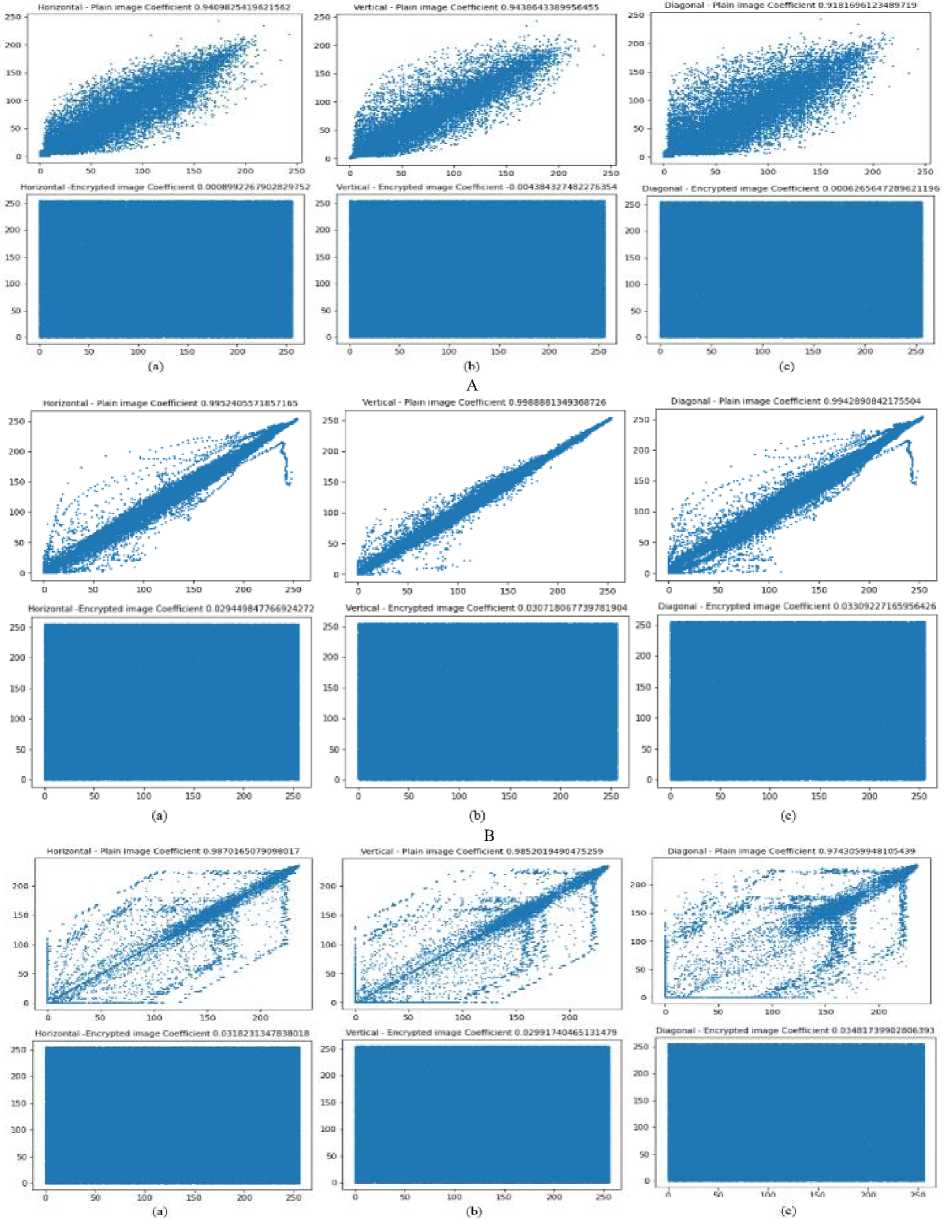
Fig.7. A correlation plot of brain MRI, COVIDx-19, and malaria image A(a), B(a), C(a) horizontal cipher image, and A(b) B(b), C(b) vertical cipher image, and A(c), B(c), C(c) diagonal cipher image

Table 9. Performance information entropy comparison with the existing approach

	Jiahui et al. [16]	Akkasaligar et al. [17]	Guan et al. [33]	Proposed scheme
Entropy	7.9993	7.8900	7.9920	7.9997

• 4.11.    Correlation Analysis

• 4.12.    Similarity Analysis

The similarity between neighboring pixels is determined using correlation analysis. If use of distinct pattern among the pixels, in that case the attackers can use that pattern to begin an assault. The coefficient of correlation should thus ideally be 0, which indicates that there is no association between neighboring pixels. The correlation of MRI scans is determined, and Table 10 displays the comparison outcome and Figs. 7 represents the vertical, horizontal, and diagonal of all three datasets.

In similarity analysis, similarities between an original picture and its associated encrypted image are examined. This similarity study used SSIM. The Multi Scale Structural similarity index function combines the SSIM index of several scaled versions of the picture to get the MS-SSIM index. To ensure that there is as little difference as possible between unencrypted images and original images SSIM values should be near 0, calculated by Eq. (9), and Eq. (10), shown in Table 11 and Table 12, respectively.

SSIM(iJ) = [p(i,j)]a . [q(i,jW . [(Шу

ms - ssiM(i,j) = [pm(i,jWM . №=i[cx(i,j)]^ . [sx(i,jWi                   (10)

(d)                                                        (e)                                                          (f)

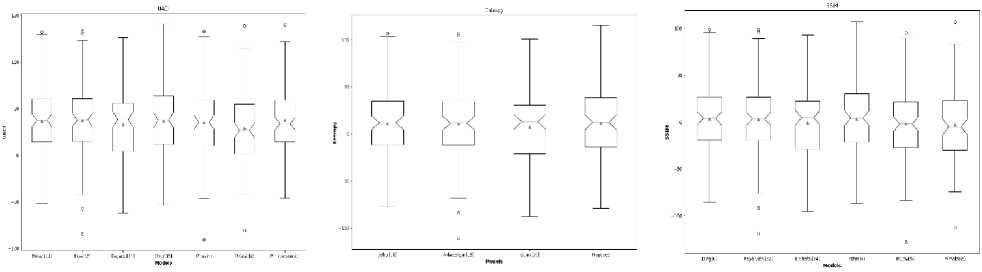
Fig.8. Comparison of performance results with an existing state-of-the-art method (a) MSE, (b) PSNR, (c) NPCR, (d) UACI, (e) Entropy, and (f) SSIM

Table 10. Performance correlation analysis of brain MRI, COVIDx-19, and malaria images comparison with the existing approach

Correlation analysis	Horizontal ↓	Diagonal ↓	Vertical ↓
Jiahui et al. [16]	0.0075	0.0072	0.0155
Akkasaligar et al. [17]	0.0194	0.0195	0.0195
Guan et al. [33]	0.0011	0.0001	-0.0002
Proposed scheme (brain MRI images)	0.0009	-0.002	-0.0021
Proposed scheme (COVIDx-19 X-ray images)	0.0090	0.0092	-0.0102
Proposed scheme (malaria microscopic images)	0.0012	-0.0010	-0.0005

Table 11. Performance SSIM comparison with the existing scheme

	Ding et al. [5]	El-Shafai et al. [22]	Kayalvizhi et al. [34]	Proposed scheme (brain MRI images)	Proposed scheme (COVIDx-19 X-rays image)	Proposed scheme (malaria microscopic images)
SSIM	0.0038	0.0051	0.0042	0.0041	0.0036	0.007

Table 12. Performance MS-SSIM comparison with the existing scheme

	Proposed scheme
	Brain MRI images	COVIDx-19 X-ray images	Malaria microscopic images
MS-SSIM	0.0181	0.0172	0.0198

• 4.13.    Discussion

The outcomes from the brain MRI dataset, COVIDx-19 dataset, and malaria dataset images are shown in Tables 4, 5, 6, 7, and 8, respectively with state-of-the-art comparison. Hua et al. [29], Belazi et al. [9], Mishra et al. [30], Honsy et al. [18], Dagadu et al. [31], Dridi et al. [32], Jiahui et al. [16], Guan et al. [33], Akkasaligar et al. [17], Kayalvizhi et al. [34], El-shafai et al. [22], and Ding et al. [5] are twelve of approaches that are compared with proposed methodology 2D-CTM shown in Fig. 8(a) to 8(f) with mean, upper and lower limit in boxplot. Since all these existing methods are used for medical image security. As shown, the proposed scheme outperforms all other existing models when it comes to security areas.

• •    The qualitative analysis for cipher image with MSE, PSNR, NPCR, UACI, entropy, SSIM, and MS-SSIM on all three datasets, respectively indicates the most significant improvement. The proposed novel deep learningbased GAN and 2D-CTM performs significantly better than all state-of-the-art approaches on medical image security.

• •    The proposed system holds promise in reducing the substantial model training overhead while improving overall performance because it uses GAN, 2D-CTM with DNA sequence, and MT approach, which is often used to improve security performance.

5.    Conclusions and Future Works

A novel proposed method-based on GAN-based chaos with DNA computing, and 2D-CTM is used for protecting images from cybersecurity risks. The medical images are encrypted by DNA encoding-based diffusion, and the MT-based confusion method is used for securing purposes. A unique GAN with 2D-CTM is presented in the proposed technique to produce the private key for processing diffusion and confusion. Moreover, after creating a key, confusion-based key sequences produced by 2D-CTM is performed followed by unique DNA encoding to complete the encryption process. The DNA-encoded and key of a biomedical image are combined using an XOR algorithm based on DNA. After that, MT-based shuffling is carried out once the image has been decoded. To create a very secure encrypted image, the key, and total number of pixels from an original image are encrypted using XOR. A comparative evaluation of the results is done while taking several security metrics, including key space, histogram analysis, PSNR enhanced with ± 1.6899%, SSIM, UACI enhanced with ± 3.1%, NPCR enhanced with ± 0.34%, MS-SSIM, and correlation analysis for COVIDx-19 X-ray, brain MRI, and malaria microscopic dataset with comparison with existing models. The proposed scheme experimental output outperforms those of other existing models. Because, it uses GAN, 2D-CTM with DNA sequence, and MT approach, which is often used to improve the performance of security. In the future, security with segmentation will be used on medical images.

Conflict of Interest

The authors declare no conflict of interest.