A Novel GRASP Algorithm for Solving the Bin Packing Problem

Published Online April 2012 in MECS

The combinatorial optimization plays a very important role in operational research, discrete mathematics and computer science. The aim of this field is to solve several combinatorial optimization problems that are difficult to solve.

Bin packing problem (BPP) is a very known optimization problem. Several real applications such as container loading, cutting stock, packaging design and resource allocation, can be modelled as bin packing problem. There are three main variants of BPP problems: one two and three dimensional Bin Packing Problems. In this paper, we deal with the one-dimensional Bin Packing Problem (1-BPP) [1, 2, 3]. 1-BPP consists to pack a set of items having different weights into a minimum number of bins which may have also different capacities. Although, this problem seems to be quite simple to define, it has been shown to be NP-complete, because it cannot be solved accurately and optimally in a reasonable time. This is the reasons, why several approximate methods have been proposed to solve this problem, which are generally based on heuristics or metaheuristics. Among the most popular heuristics used to solve the bin packing problem, the First Fit algorithm (FF) which places each item into the first bin in which it will fit. The second popular heuristic algorithm is the Best Fit (BF) which puts each element into the filled bin in which is fits. Moreover, the FF and BF heuristics can be improved by applying a specific order of items like in First Fit Decreasing (FFD) and Best Fit Decreasing (BFD), etc [4,5,6]. Moreover, many kinds of metaheuristics have been used to solve the bin packing problems like genetic algorithms [7], Ant colony [8],etc.

Greedy Randomized Adaptive Search Procedure (GRASP) is a metaheuristic algorithm usually applied successfully to several combinatorial optimization problems [9, 10, 11]. A GRASP is an iterative procedure, where each GRASP iteration consists of two phases: construction and local search. The construction phase is greedy procedure used to build a feasible solution. The second phase is a local search which is used to enhance the solution found by the first phase of the GRASP procedure. The two phases are repeated several times independently or using a certain learning scheme and the best overall solution is selected as the final result. In order to deal with an optimization problem by using a GRASP procedure, it is necessary to define at least the following elements integrated in the heuristic [9]:

• •    The randomized greedy procedure used during the first phase of the GRASP algorithm,

• •    The solution’s neighborhood structure and which technique should be used to investigate it,

• •    The stopping criterion.

The stochastic local search methods were demonstrated to be useful in solving many complex problems. Tabu Search (TS) [12] is among the most popular and robust local search methods. TS is found to be practical in many hard combinatorial optimization problems. The main idea underlying is to diversify the search and avoid becoming trapped in local by forbidding or penalizing moves which take the solution, in the next iteration, to point in the solution space previously visited. For this, the algorithm creates a memory list of undesirable moves called "tabu list". However, Tabu restrictions may be overruled under certain conditions, in which, a Tabu move leads to a better solution, this principle is called aspiration criterion. The main difficult of the tabu search is the choice of the best parameter setting [12, 13].

The present study was designed to investigate the use of the GRASP algorithm to deal with the one dimensional bin packing problem. The first phase consists of the construction of good solutions by means of a new greedy algorithm. This later is based on a hybrid heuristic based on both first fit (FF) and best fit (BF) heuristics. In order to generate diverse solution, some randomness is inserted in the core of the proposed heuristic. The second phase of GRASP is based on tabu search algorithm. The idea consists in choosing randomly a filled bin, and then we empty it. Afterwards, the unpacking objects are packed in the other available bins by using the first fit strategy. The experiences carried out on the proposed approach showed the feasibility and the effectiveness of our approach.

The remainder of the paper is organized as follows. In section 2, a formulation of the tackled problem is given. In section 3, the proposed method is described. Experimental results are discussed in section 4. Finally, conclusions and future work are drawn.

• II.    Problem formulation

Bin packing problem is an important task in solving many real problems such as the loading of tractor trailer trucks, cargo airplanes and ships, etc. For example, the container loading problem consists to design an affective loading plan for containers. It consists of finding the most economic storage of articles that have all the same dimensions but with different weights in containers (also called bins) of equal capacity. The constraint is that the bins do not exceed its capacity. This problem can be modeled as a one-dimensional bin packing problem. The principal objective is to minimize the number of bins used for storing the set of all items. Formally, the bin packing problem can be stated as follows:

Min z (y) = E у,(1)

j = 1

Subject to constraints:

n g «x ^ cy      j e n *+

n

Ц xj=1             j e N *+ y , Xj e{0,1}            i, j e N *+

With :

y i = 1   if the bin i is used; else 0

x ij = 1 if the item j is stocked in bin i .

In the above model the objective function is to minimize the total number of bins used to pack all items which have the same capacity ( eq.1). The first constraint guarantees that the weights of items (w i ), placed in bin j, do not exceed the bin capacity. The second constraint ensures that each item is placed only in one bin. It appears to be impossible to obtain exact solutions in polynomial time. The main reason is that the required computation grows exponentially with the size of the problem. Therefore, it is often desirable to find near optimal solutions to these problems. Efficient heuristic algorithms offer a good alternative to accomplish this goal. Within this perspective, we are interested in applying a GRASP algorithm.

• III.    The proposed approach for bin packing

PROBLEM

To solve the bin packing problem, we propose a new algorithm based on Greedy Randomized Adaptive Search Procedure (GRASP). GRASP is a two-phase metaheuristic technique used to solve hard combinatorial optimization problems. The first phase is a construction phase used for the construction of initial solutions, while the second phase is generally a local search method used for the improvement of the solutions found in the first phase [10]. A generic GRASP approach is described in Figure 1. In more detail, the proposed approach based GRASP for BPP problem is given by the Figure 2.

Input: seed, Number_iteration

Output: Best_solution

Initialization.

repeat

• a.    Solution=Constructive_phase(seed);

• b.    Local_Search(Solution,seed);

• c.    Best_solution=

Update_solution(Solution);

until (Number_iteration)

End

Figure 1 ． The GRASP metaheuristic scheme.

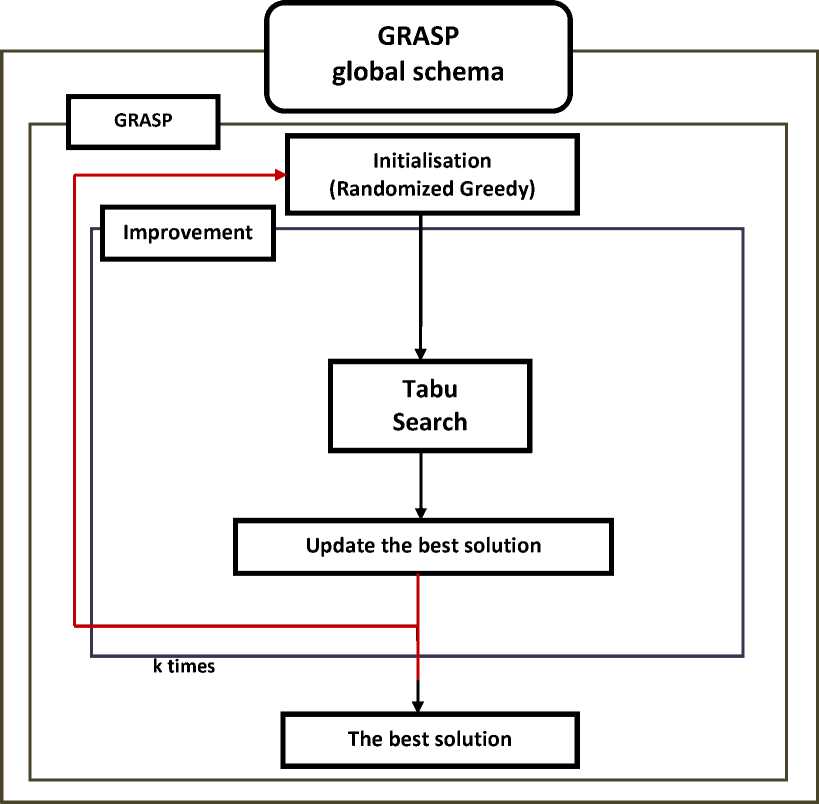
Figure. 2 The GRASP flowchart for Bin packing problem.

• A.    The construction phase

The first phase of the proposed GRASP algorithm is to build gradually a feasible initial solution by using a greedy randomized procedure, whose randomness allows exploring efficiently the solution space. In this paper, we have proposed a new stochastic greedy algorithm to construct trial solutions. The new hybrid greedy algorithm is based on both First Fit (FF) and Best Fit (BF) heuristics. Consequently, the resulting heuristic takes advantages from both of FF and BF heuristics. In order to obtain diverse solutions, we have introduced some randomness in the greedy phase. With some probability, we can select the BF algorithm instead of FF algorithm to pack items in bins. If the BF is selected, a nonempty bin is randomly selected; and the available items are packed in the bins from the selected bin until the last used bin by using the BF technic. In more detail, the proposed random hybrid heuristic is described by the following Figure.

Input: Number of items, weights of items Ouput: Bin packing solution

Begin

Repeat

It= select_item; pr = random();

if (pr > 0.3)) then apply the FF to pack it;

else ibin= randInt (1,nbins);

//nbins: nbr of nonempty bins +1

Apply the BF to pack it from ibin until nbins;

end if until(the packing of all items)

End

Figure 3. Random hybrid heuristic for bin packing problem

The following example illustrates the difference between the standard heuristics algorithm and the proposed random greedy algorithm. In this example, we have 14 items to pack. The second line contains the item weight:

1	2	3	4	5	6	7	8	9	10	11	12	13	14
13	5	7	1	12	7	10	9	14	6	4	1	8	3

If we apply only the First Fit algorithm, we get the following solution for every execution:

1

1

2

1

2

3

3

4

5

4

4

1

6

3

However, the following tables contain different solutions obtained by the rerun of the proposed random greedy algorithm several times. By consequent, the proposed stochastic heuristic offers a great diversity to the GRASP algorithm.

5

5

2

5

3

4

6

6

1

1

4

5

3

4

1	3	1	5	3	5	5	4	2	4	6	5	6	3
2	6	2	6	6	1	1	3	4	3	3	6	5	1

• B.    Local Search phase

The solutions obtained in the construction phase are generally not optimal. GRASP uses an improvement phase, in order to enhance the built solutions. Generally, the second phase is a local search method however we can use other metaheuristics like genetic algorithm. In our approach, we have used the tabu search algorithm (TS), because it is a powerful local search algorithm, and it is widely used in combinatorial optimization problems. In more detail, the tabu search method is given by the following figure.

Input: a solution for Bin packing problem

Ouput: an improved solution begin

S = initial solution ;

Best = S ;

repeat

Sbest = the_best_neighbourhoud( S);

if (fitness(S_best) < fitness (Best)) then Best = Sbest ;

Update the_tabou_list

S = S best ;

until ( stopping criteria are satisfied) return Best ;

Fin

Figure 4. Tabu search procedure.

Obviously, the choice of an appropriate neighbourhood is the most important step to obtain a powerful local search algorithm. In our algorithm, the neighbourhood structure is chosen as follows: from the initial solution obtained in the construction phase, a bin is randomly selected. Then, all the items of the selected bin are packed in the other bins by using the First Fit strategy. This is process is repeated until the satisfaction of the termination criterion.

• IV.    Experimental Results

We have implemented our approach in Matlab 7.7 and tested on home PC with core duo processor and 2.2 GB of memory. In order to evaluate the proposed approach, we have used a set of benchmark data sets taken from the site The benchmark data sets are divided into three classes: easy, medium and hard class instances. A description of the used instances is summarized in Table 1. We have used 400 iterations for GRASP algorithm and 1600 iterations for tabu search.

Table 1 contains the experimental results, the first column is the name of the instance, the second column contains the number of variables, the third contains the bin capacity, the fourth column contains the results of the greedy approach, the fifth column contains the results of the GRASP approach, and the last column contains the best know results. Moreover, we have used the Friedman tests for comparing statistically the found solutions.

In term of rapidity, the proposed GRASP-based approach is slower than the greedy algorithm. However, in terms of solutions quality, the GRASP algorithm is largely better than the greedy algorithm in the three classes of tests as it’s showed by the Freidman tests (Figures 5, 6, and 7). On the other hand, the obtained results of our approach are very close to the optimal solution. We can note that the differences between the solutions found by our approach and the best know ones are between 0 and 3. Figure 5 shows that for the first series of easy-type instances, the obtained results of our algorithm are completely identical to the best known solutions, while those of greedy algorithm are very distant from the best known solutions. In The second series of medium instances, the greedy algorithm is not successful in this experiment; it’s very far from the best known solutions. However, there is no great difference between the results of our approach and the best know solutions (Figure 5). Finally, Figure 7 shows that for the third series of hard instances, our algorithm ranks second in the Friedman test after the best known solutions. However, the greedy approach is also not successful in this test.

The effectiveness of our approach is explained by the good combination between the diversification of the random greedy phase and the intensification of the tabu search which leads the algorithm to explore effectively the search space and locate a good solution.

TABLE I.      The bin packing results, n: number of items, C:

bin capacity.

Instance	N	C	Greedy	GRASP	Best known
N1C2W4_C (easy)	50	120	30	30	30
N2C3W4_T (easy)	100	150	47	46	46
N2C3W4_L (easy)	100	150	46	45	45
N3C1W1_A (easy)	200	100	106	105	105
N4C1W1_M (easy)	500	100	246	246	246
N1W1B1R0 (medium)	50	1000	20	18	18
N1W1B1R1 (medium)	50	1000	20	19	18
N1W1B1R2 (medium)	50	1000	20	19	19
N1W1B1R3 (medium)	50	1000	20	18	18
N1W1B1R7 (medium)	50	1000	19	18	18
N2W1B1R0 (medium)	100	1000	37	35	34
N2W2B1R4 (medium)	100	1000	22	21	21
N2W4B2R2 (medium)	100	1000	12	11	11
N3W2B1R6 (medium)	200	1000	44	42	41
N3W3B1R1 (medium)	200	1000	30	29	28
N3W4B2R1 (medium)	200	1000	23	22	22
N4W3B2R5 (medium)	500	1000	73	72	72
N4W3B2R7 (medium)	500	1000	72	71	70
N4W4B1R5 (medium)	500	1000	58	57	56
N3W1B1R7 (medium)	200	1000	73	68	67
HARD2	200	100000	60	59	56
HARD6	200	100000	60	59	57
HARD7	200	100000	59	58	55
HARD8	200	100000	60	59	57
HARD9	200	100000	60	58	56

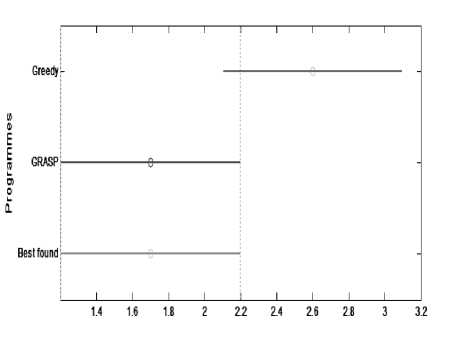
Figure 5. Friedman test for easy-type instances.

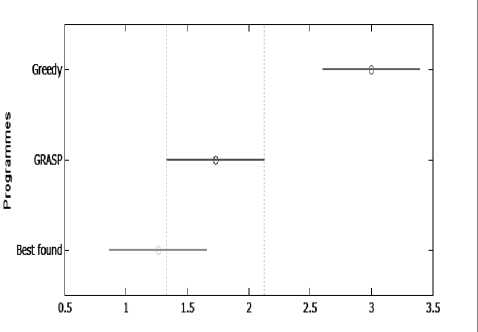
Figure 6. Friedman test for medium-type instances.

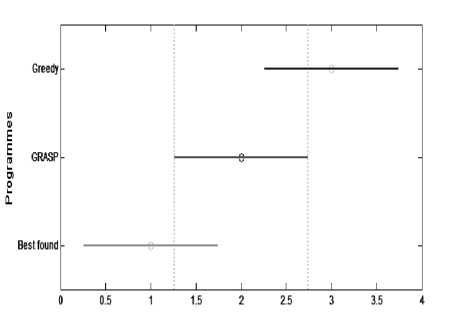
Figure 7. Friedman test for HARD-type instances.

• V.    Conclusion

We have tackled in this paper the one-dimensional bin packing problem. The importance of this problem lies in its widespread applications in transport, loading and industry. Unfortunately, this problem belongs to the class of NP-hard problems. To solve this problem, we have proposed in this paper, a new hybrid method based on the GRASP metaheuristic. The first phase of our algorithm is based on a new hybrid greedy algorithm, which uses both FF and BF heuristics to build diverse initial greedy solutions. The great feature of this stochastic heuristic is its great ability to build rapidly good random solutions. In the second phase of our algorithm, the tabu search procedure is used in order to improve the solutions built in the first phase. To assess the performance of the proposed approach, several experiments have been done. The results are very encouraging and clearly show the effectiveness of our approach. As perspective, we want to test the effectiveness of other local search methods such as simulated annealing, variable neighbourhood search, etc. we can also use other heuristics to build the initial solution like FFD or BFD.