A Novel Image Encryption Scheme based on a Nonlinear Chaotic Map

Published Online November 2010 in MECS

With the rapid development of multimedia technology and Internet, digital images and other multimedia are more commonly and frequently transmitted in the public communication network. Therefore, the security of image data attracts more and more attention, and image encryption technology becomes an important issue of cryptography. Image data have strong correlations among adjacent pixels. Statistical analysis on large amounts of images shows that averagely adjacent 8 to 16 pixels are correlative in horizontal, vertical, and diagonal directions for both natural and computer-graphical images [1]. Moreover, due to some intrinsic features of images, such as bulk data capacity and high redundancy, encryption of images is different from that of texts [2]. Therefore, conventional cipher algorithms such as DES, IDEA etc. are not suitable for image encryption. The chaos-based cryptography has suggested a new and efficient way to develop fast and secure image encryption algorithms.

Matthews first proposed the chaos-based encryption scheme in 1989 [3], and Fridrich first adopted chaotic map into image encryption in 1997 [4]. Since then, many chaos-based image encryption algorithms have been designed to realize secure communications [1, 4-12], but it is pointed out that most of them are flawed by lack of robustness and security [10-14].

In [6, 7], a type of chaotic encryption scheme which was based on circular bit shift and XOR operations was proposed. In this type algorithm, the plaintext block was permuted by a circular bit shift approach and then encrypted by the XOR operation. However, it was shown that there are some defects with this type algorithm in [11-13]: 1) Low sensitivity of encryption to plaintexts. 2) Not secure against the chosen plaintext attack. In [13], the type algorithm was cryptanalysis by chosen plaintext attack and improved to avoid chosen plaintext attack, but the first defect exists in the improved scheme yet. It is necessary to note that the improved scheme also has low sensitivity to small changes of the plaintext. If a plaintext byte is changed, only the ciphertext bytes behind the corresponding ciphertext byte are changed, i.e., it has no effect to the ciphertext bytes before the corresponding ciphertext byte.

Based on a permutation approach and the XOR operation, a type of chaotic image encryption algorithm was proposed in [1, 15-19]. In this type encryption scheme, the plain-image was first permutated and then substituted, or was first substituted and then permutated. It has been pointed out that the type algorithm also has the two defects which are described in the above paragraph [20].

In [21, 22], a type of image encryption scheme which employs an image total shuffling matrix to shuffle the positions of image pixels was present. In the schemes, the image was shuffled based on a total image shuffling matrix generated by a chaotic map, and then the shuffled image was encrypt based on XOR operation by another chaotic map. Unfortunately, the two defects were founded in the type of algorithm, too [14]. Though the ciphertext feedback method was adopted in [22], the encryption scheme still has low sensitivity to small changes of the plaintexts.

A new class of chaos-based image encryption schemes was proposed [23-25]. In this class of algorithms, the plain-image Pm×n was transformed into the plaintext matrix M(mn)×1 firstly, and then this matrix was encrypted using results of iteration of chaotic maps to obtain a new modified message matrix M. Finally, the whole process was repeated for the new M from the last element to the first one, and new matrix C was the output as the ciphertext. To enhance the security, a small perturbation was given to the parameters of chaotic maps based on the last obtained encrypted element.

In this class of schemes and most other classes of chaos-based encryption algorithms, each time a one-dimensional chaotic map is iterated, only a single byte random number can be generated. To accelerate the encryption speed and to enhance the security, an improved image encryption scheme is proposed by means of three other measures in this paper. First, there are two rounds in the proposed scheme. Second, every time NCM is iterated, n ( n >3) bytes random numbers can be gained so as to accelerate the encryption speed. Finally, a piecewise linear function is used, which can make sure that the perturbation isn’t too small. Based on the last obtained n bytes modified elements, only the parameters of the NCM are perturbed before next iteration. So the state transfer function not only depends on the secret key, but also depends on the output ciphertext. Therefore, the proposed scheme can resist chosen plaintext effectively.

The rest of the paper is organized as follows: Sec. 2 gives a brief introduction of the nonlinear chaotic map. A chaos-based image encryption scheme is proposed in Sec. 3. Sec. 4 shows the simulation result. The security analysis is given in Sec. 5. Finally, Sec. 6 concludes the work.

• II.    TH E NONLINEAR CHAOTIC MAP

Chaos, which has many good properties, such as the ergodicity, sensitive dependence on initial conditions and random-like behaviors, is an aperiodic dynamics process, seeming disorderly and unsystematic [26]. In fact, the properties just suit to the diffusion and confusion process in cryptography [1, 8].

One-dimensional chaotic system which has the advantages of high-level efficiency and is implicit [27], such as Logistic map, is being widely used now. But their weaknesses, such as small key space and weak security, are also known to us obviously [28]. With more than one control parameters and initial conditions, high dimensional chaotic systems are most complex and have a big key space. However, complex calculations make the encryption algorithm too slow.

To overcome these drawbacks, a nonlinear chaotic map (NCM) [29] is adopted in this paper:

( a AC 1 a ^в

xn,+1 = (1 - P\ctan 7-T • 1+ -T

V ^{1 +} P 7 V P 7      ⁽¹⁾

• tan (axn )^(1- x)в where a , в are control parameters. When xn e (0,1), ae (0, 1.4), pe [5, 43], or xn e (0,1) , ae (1.4, 1.5], в e[9, 38], or xn e (0,1) , ae (1.5, 1.57], в e[3, 15], NCM performs chaotic phenomena.

It is shown that the system NCM is a chaotic system with good properties of balanced 0–1 ratio, zero co-correlation and ideal nonlinearity, while maintaining acceptable efficiency in [30].

In order to get a faster encryption speed, every time NCM is iterated, n bytes random numbers can be gained In this paper. Suppose that X = 0. x 1 X 2 L x 15 ^L is a double-point value, the n bytes decimal random numbers are generated as follows:

B i = mod⁽x 3 _n , i x4 _n x 5 _{n +} i , ²⁵⁶⁾ , ⁽²⁾ where i = 1,2, L , n , mod( x , y ) returns the remainder after division, X ^ = 0,1, L , 9 , 4 <  n <  13 . If n =4, for example, four bytes random numbers B 1 =mod( x 10 x 11 x 12 , 256), B 2 =mod( x 11 x 12 x 13 , 256), B 3 =mod( x 12 x 13 x 14 , 256) and B 4 = mod( x 13 x 14 x 15 , 256) will be gained.

• III.    THE PROPOSED IMAGE ENCRYPTION SCHEME

Given an image plaintext p_ij ( i =0, 1, L , M -1; j =0, 1, L , N -1), suppose the secret key K = K ( K 1 ; K 2 ) = ( a ¹, p ¹, x 0 ; a ², в ², x 2 ), where the sub-key K 1, K 2 include the control parameters and the initial conditions of the NCM. The proposed scheme which is shown in Figure 1 is described below.

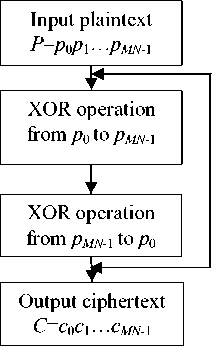
Figure 1. Encryption scheme, m =2.

Step 1 Arrange the plain-image p_ij ( i =0, 1, L , M -1; j =0, 1, L , N -1) by the order from left to right and then top to bottom, and a plaintext matrix P = p ₀, p ₁, L , P_MN 1 can be obtained.

Step 2 Choose the first sub-key K 1 = ( a ¹, в , x 0 ) , and then iterate NCM (1) n 1 times to avoid the transient effect.

Step 3 Iterate NCM once, n bytes random numbers can be gained by Eq. (2), and then encrypt the message ^block P = P nj , P nj ₊ 1 , ^L , P nj + n - 1 ^as follows:

^Cnj + k = P j + k ® a nj + k         ⁽³⁾

where ф is the XOR operation, and k =0, 1, L , n — 1 .

Step 4 If all the plaintext has already been encrypted, then the encrypted message matrix M = C0, Cv L , CMN—1  is obtained, and turn to Step 5. Otherwise, j = g («j, Cnj, cnj+1, L , Cnj+n—1 ) , Pj+X = h (вj, Cnj, Cnj +1, L , Cnj+n—1 ) , where g and h are piecewise linear function in Eq. (4) and Eq. (5), then let j=j+1 and turn to Step 3.

tx,=g(tx,c,c,,L,c ,) = j+1 g j , nj , nj + 1, , nj + n—1

Step 6 Do step 2-5 for the matrix C again, and the final ciphertext can be gained. Rearrange the ciphertext into the cipher-image, and the encryption process is finished.

In this scheme, suppose that m =mod( MN , n ). If m >0, we can only generate m random numbers in the last block, or let p k =0 ( k = MN , L , MN + n - m -1) and MN = MN + n - m . The decryption process is almost the same as the encryption one. We only need to do the XOR operation by the second sub-key K 2 from the last byte to the first byte for the ciphertext matrix C to obtain the modified message matrix M first, and then do the XOR operation for matrix M from the first byte to the last byte by the first sub-key K 1 . Do the above process again, and finally the plaintext matrix P can be recovered.

• IV.    EXPERIMENTAL RESULTS

  n — 1

  У ^Cnj + k ^{+ 10 n}

  a — —-----

  ^j     2560 n

  
  

  ^a j

  
  

  a j

  
  

  n — 1

  c

  nj + k

  _ k = 0

  2560 n ^,

  n — 1

  У ^Cnj + k ^{+ 10 n}

  + k =0 _____________

  2560 n

  
  

  a _j

  
  

  n — 1

  c

  Z—i nj + k

  + k =0 ______

  2560 n

  
  

  n — 1

  ^a j >  ^a 0 , У ^Cnj + k <  ^{10 n}

  k = 0

  n — 1

  ^a j >  ^a 0 , У ^Cnj + k >  ^{10 n} (4) k = 0

  n — 1

  ^a j ^ ^a 0 , У ^Cnj + k <  ^{10 n}

  k = 0

  n — 1

  ^a j <  ^a 0 , У ^Cnj + k >  ^{10 n}

  k = 0

  
  

  The experimental results are shown in this section. Take a 256 grey-scale BMP plain-image of size 256×256 for example. The secret key is chosen as K = ( a ¹, в ¹, x 0 ; a ², в 2 , x 0 ) =(1.1, 6.0, 0.5432106789017177; 1.1, 6.001, 0.5432106789017177). Figure 2 shows the experimental results of the proposed scheme. Figure 2(a) is the plain-image Lena.bmp. Figure 2(b), (c) and (d) are the corresponding encrypted images when n =4, 8 and 9. From Figure 2(b), (c) and (d), we can see that the encrypted images are rough-and-tumble and unknowable, so the diffusion and confusion properties are confirmed.

  
  

  P j +1 = ^{h (} P j , ^Cnj , ^Cnj + 1 , ^L , ^Cnj + n — 1 ) =

  
  

  n — 1

  У ^Cnl + k ^{+ 10} n            n — 1

  Р,- - i = 0            , P , > P „ , У C , + ,

  256000 n            k ~ 0

  
  
  

  (a) Plain-image

  
  
  

  (b) n =4

  
  

  < 10 n

  
  

  n — 1

  C - . nj + k

  в — k =^ ----,

  ^j 256000 n

  
  

  <

  p j

  
  

  n — 1

  У ^Cnj + k ^{+ 10 n}

  + k =0 _____________

  256000 n

  
  

  I ^е -

  
  

  n — 1

  c

  Z^ nj + k

  + - k =0------- ,

  256000 n

  
  

  n — 1

  P , > p « , У C n, . k ^ 10 n k = 0

  в < P o , У 1 C n„, <  10 n

  k = 0

  n — 1

  P j < в о , У C „ + k >  10 n

  k = 0

  
  
  
  
  

  (c) n=8

  Figure 2. Encryption experimental results

  
  
  

  (d) n =9

  
  

  Step 5 Choose

  
  

  the second sub-key

  
  

  K ₂ = ( a ², в ², X 2 ) , and then iterate NCM n ₂ times.

  
  

  Let M ' = C_{MN — 1}, C MN _{— 2}, L, C ₀ , and encrypt M ' using the method described in Step 3 and Step 4. Finally, the encrypted matrix C can be obtained.

  
  

  All the simulation experiments are implemented using Visual C++ 6.0 and running in a personal computer with Pentium (R) D CPU 2.80 GHz 2.79 GHz, 1.00 GB memory, 160 GB hard-disk capacities. The time used in encryption on 256 grey-scale BMP images of size 256×256 with different values of n is shown in Table I. It is shown that the proposed algorithm is fast enough for practical transmission of image files over public

  
  

communication network. For different practical demands of encryption speed, we can choose a suitable value of n .

• V.    SECURITY ANALYSIS

To show the satisfactory security of the proposed scheme, some security analyses on the proposed encryption scheme, including the most important ones like key space analysis, information entropy, correlation analysis of two adjacent pixels and differential analysis, are shown in this section.

• A.    Key space analysis

The key space of a good encryption scheme should be large enough to make brute-force attacks infeasible. Two groups of secret keys, including the initial values and the control parameters of the NCM, are employed in our encryption algorithm. Suppose that the precision is 10-15, the key space size of the proposed scheme is ((1015)3)2=1090. Therefore, the key space is large enough to resist all kinds of brute-force attacks.

• B.    Information entropy

It is well known that the information entropy is defined to express the degree of uncertainties in the system. The information entropy is defined as follows:

TABLE I. E NCRYPTION TIME

n	4	5	6	7	8	9	10	11
Encryption time (S)	0.12669	0.10246	0.086579	0.075185	0.066874	0.061955	0.055768	0.051060

TABLE II.

I NFORMATION ENTROPY

n	4	5	6	7	8	9	10	11
Entropy H	7.9974	7.99701	7.99707	7.99686	7.99756	7.99675	7.99722	7.99708

TABLE III ．

Information entropy with different key

(a) Plain-image

(b) n =4

(c) n =8

(d) n =9

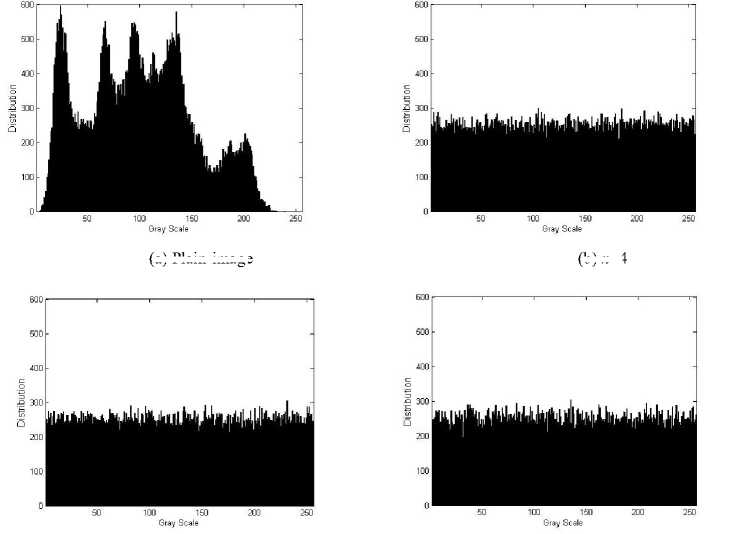
Figure 3. Grayscale histogram of plain-image and cipher-images

	n =4	a	b	c	d
Entropy H	7.9974	7.9972	7.99717	7.99708	7.99706

TABLE IV.

C ORRELATION COEFFICIENTS OF TWO HORIZONTALLY ADJACENT PIXELS

	Plain-image	n =4	n =8	n =9
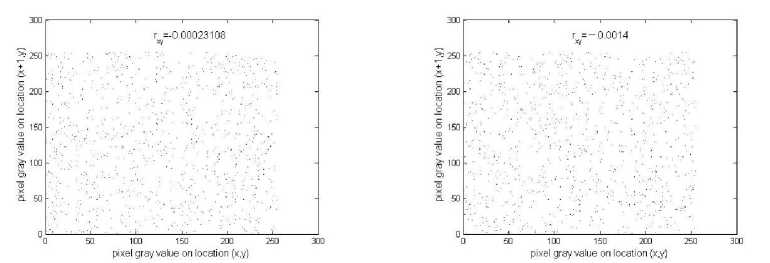
correlation coefficients	0.9671	0.0029	-0.00023108	－ 0.0014

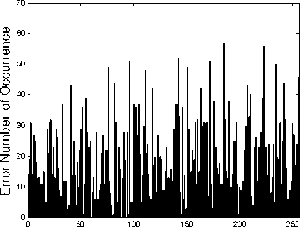
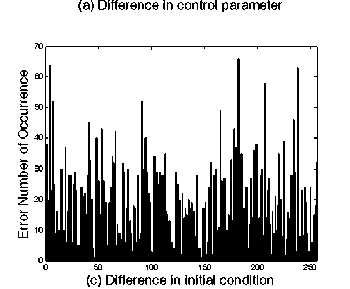
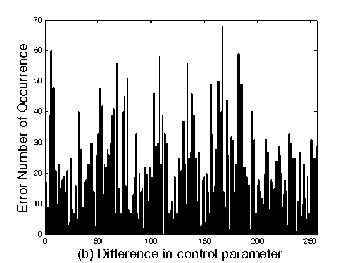
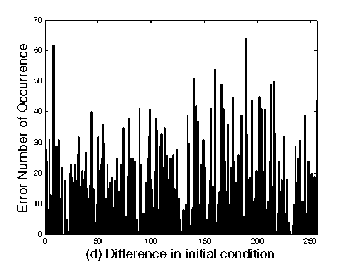
Figure 4. Distribution of error ciphertext

(a) Plain-image

(b) n =4

(c) n =4

(d) n =4

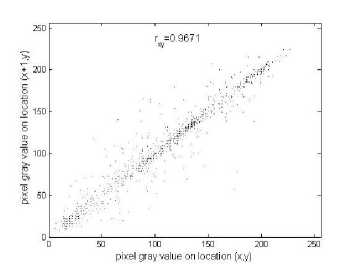
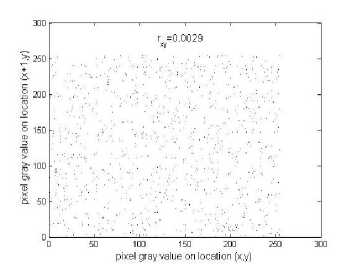
Figure 5. Correlations of two horizontally adjacent pixels

2 ^N - 1

H(m) = -E P(mi ) log2[P(mi)] , i=0

where P(mi ) is the emergence probability of mi . If every symbol has an equal probability, i.e., m = {m0, m1,L , m28-1} and P(mi) = 1/28 (i=0, 1, L , 255), then the entropy is H(m)=8, which corresponds to a random source. Usually, the practical information entropy is less diverse than the ideal one. The information entropy is respectively shown in Table II, which is very close to the ideal one, by different n.

• C.    Statistical analysis

• a)    Gray-scale histograms

Considering the statistical analysis of the plain-image and its encrypted images, the grey-scale histograms of them are shown in Figure 3. From Figure 3(b), (c) and (d), we can see that the grayscale distribution of encrypted image has good balance property, which is strongly against known plaintext attacks.

In order to show the small perturbations of unknown key parameters, we will show the distribution of Error Ciphertext [7] which means the error number occurrences between the encryption system in the above section and the incryption system with small perturbations of unknown keys listed as follows:

• (a)    a = 1.0999999999;

• (b)    в ² = 6.0010000000001;

• (c)    x 0 = 0.5432106789017176;

• (d)    x 02 = 0.5432106789017178;

the others are the same as those in Sec. IV. The distribution of Error map is shown in Figure 4, respectively. And the information entropy of them is respectively shown in Table III. It is shown that even a small variation of system parameters may result in the wrong encryption maps. Therefore, it is really hard to reveal the original cryptosystem.

• b)    Correlation analysis

  To test the correlation between two adjacent pixels in plain-image and cipher-image, the following procedure was carried out [2]. First, select 1000 pairs of two adjacent (in horizontal, vertical, and diagonal direction) pixels from an image randomly. Then, calculate the correlation coefficient of each pair by using the following formulas:

1N

cov(x, y) = N§ E (x - E(x))(y - E (y)) , i=1

= cov( x , y ) D ( x ) D ( y ) ^,

v xy

where x and y are grey-scale values of two adjacent pixels in the image. In numerical computation, the following discrete formulas are used:

1N

E(x)=N § x"

N

D (x) = 77 § (xi— E (x ))2.

N 7 = 1

TABLE V ．

C ORRELATION COEFFICIENTS OF TWO ADJACENT PIXELS

	Plain-image	Cipher-image
Horizontal	0.9671	0.0029
Vertical	0.9339	0.0096
Diagonal	0.9066	0.0054

Figure 5 shows the correlation distribution of two horizontally adjacent pixels in the plain-image and that in the cipher-image when n =4, 8, and 9, and the correlation coefficients are shown in Tab. IV. It is shown that the correlation coefficients of two horizontally adjacent pixels in the plain-image and that of the cipher-image are far apart. Similar results for vertical and diagonal directions are obtained, which are shown in Table V when n =2. These correlation analyses prove that the chaotic encryption algorithm satisfies zero co-correlation.

• D.    Differential analysis

TABLE VI ．

D IFFERENTIAL ANALYSIS ( KA )

n	NPCR(%)	UACI(%)
4	0.492859	0.331024
5	0.497437	0.330658
6	0.497437	0.330826
7	0.500449	0.331451
8	0.497437	0.330856
9	0.492859	0.330795
10	0.492859	0.330627
11	0.503540	0.331329

TABLE VII ．

Differential analysis ( KB )

n	NPCR(%)	UACI(%)
4	0.512695	0.330750
5	0.502014	0.330338
6	0.508118	0.330826
7	0.486755	0.330994
8	0.495911	0.331116
9	0.506592	0.330597
10	0.492859	0.330765
11	0.497437	0.331238

To test the influence of one-pixel change on the whole image encrypted by the proposed algorithm, two common measures, NPCR and UACI [2], were used. NPCR means the change rate of the number of pixels of ciphered image while one pixel of plain-image is changed. UACI which is the unified average changing intensity, measures the average intensity of the differences between the plain-image and ciphered image.

Denote two cipher-images, whose corresponding plain-images have only one-pixel difference, by C 1 and C 2 , respectively. Label the grey-scale values of the pixels at grid ( i , j ) of C 1 and C 2 by C 1 ( i , j ) and C 2 ( i , j ), respectively. Define a bipolar array, D , with the same size as image C 1 or C 2 . Then, D ( i , j ) is determined by

C 1 ( i , j ) and C 2 ( i , j ), namely, if C 1 ( i , j )= C 2 ( i , j ) then D ( i , j )=1; otherwise, D ( i , j )=0. To resist differential attack, the NPCR value should be small enough, and the UACI value should be large enough for an ideal cipher system.

Tests have been performed on the proposed scheme, about the one-pixel change influence on a 256 grey-scale image of size 256×256. With two different keys, KA and KB the results are shown in Table VI and Table VII. According to the two tables, the proposed cryptosystem can achieve a high performance such as NPCR<0.5127% and UACI>0.33033% when n <  11 . Therefore, the proposed algorithm can resist differential attacks.

• VI. CONCLUSION

Only by the XOR operation, a novel image encryption scheme based on NCM is proposed in this paper. Every time the NCM is iterated, n ( n >3) bytes random numbers can be gained so as to improve the encryption speed, and before next time iteration, a small perturbation will be given to the parameters of NCM based on the last obtained n bytes message. In each round of the proposed scheme which includes two rounds, the message P = p ₀, L , P j , L p MN - 1 is modified in the ascending order of j firstly, and then the modified message is encrypted in the descending order of j . Simulation results show that the new cryptosystem is fast, which makes the transmission of large multi-media files over public data communication network more practical. Theoretical analysis indicates that the proposed chaos-based image encryption scheme can achieve a high performance and is secure against known/chosen plaintext attack and all kinds of brute-force attacks.

ACKONOWLEDGMENT

This work is supported by the Natural Science Foundation of China (No. 60973146 and No. 61070163), the Natural Science Foundation of Shandong Province, China (ZR2009GM036), the Foundation for Study Encouragement to Middle-aged and Young Scientists of Shandong Province, China (No. 2008BS01019).