A Novel Minimized Computational Time Based Encryption and Authentication Using ECDSA

Published Online October 2013 in MECS DOI: 10.5815/ijmecs.2013.09.03

The todays era most of data are sent via the internet for sharing, so the trust of data files is decreased. For the trust more security and authentication is needed, less security increase the liability of attacks on data. The digital signature of the data is a solution to this security problem which provides the reliability, authenticity and accuracy. Basic algorithms for security and authentication is RSA, DSA, algorithms which use the different key of different sizes. This paper proposes a novel ECDSA algorithm to encrypt the data. It uses a parameterized hash algorithm to authenticate the data and also compare both RSA and ECDSA methods in respect of time parameters.

The branch which deals with the making of algorithms for encryption and decryption to provide the security properties authenticity and secrecy of information is cryptography [1]. Less security grows on application level or network level by different types of active and passive attacks are introduced in these days. To protect a user's identity from being read or modify (Data integrity), we need security. For a message which is signed and encrypted, the message is signed once and the signature is verified by each recipient. The message is encrypted with each recipient’s public key by the sender using a symmetric key, and must decrypt his encrypted document by the symmetric key. Some factors like flexible, security of a digital signature algorithm and speed problem of signing and verifying in digital signature must be considered an important issue. In practical application, security is often influenced by machines’ operating speed. And transmitting speed is a big bottleneck especially in a network environment [2]. So, operation should be simplified and also ensure safety. There are data protections prototypes are used to transmit data across the network. These prototypes take more time to efficiently provide the security.

In this paper we are developing such a system which can perform such type of tasks. We are developing a system which can find reduce the computational time and complexity of the basic algorithms of encryption and authentication.

• II.    BACKGROUND

In data and telecommunications, cryptography is necessary when communicating over any un-trusted medium, which includes just about any network, particularly the Internet. The security goals like integrity, confidentiality and authentication can be completed by using the digital signature encryption and decryption methods with time stamping. For the trust more security and authentication is needed. Still a number of methods are currently available to protect data while transmitting across the network [3]. These methods provide the security but it consume the more time for reducing the computation time we are using the ECDSA and using the PHAL for more security and it provide the better result with compare to the other secure system. The digital signature scheme is based on elliptic curve and proactive secret sharing. This scheme make up for the lack of exiting schemes, possessed stronger security, and from the view of application, the new scheme was more practical. And the PHAL is more delicate hash algorithm to compare with the SHA/MD. PHAL reduce the weakness of the SHA/MD and provide the high security.

Within the context of any application-to-application communication, there are some specific security requirements, including: authentication, privacy/confidentiality, integrity, non-repudiation. There are several ways of classifying cryptographic algorithms. For purposes of this paper, they will be categorized based on the number of keys that are used for encryption and decryption, and further defined by their application and use [4]. The three types of algorithms that will be discussed are:

• [1]    Secret Key Cryptography (SKC): Uses a single key for both encryption and decryption

• [2]    Public Key Cryptography (PKC): Uses one key for encryption and another for decryption

• III.    RELATED STUDY

The digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit. Digital signatures employ a type of asymmetric cryptography. For messages sent through a non-secure channel, a properly implemented digital signature gives the receiver reason to believe the message was sent by the claimed sender. Digital signature schemes in the sense used here are cryptographically based, and must be implemented properly to be effective. Digital signatures can also provide non-repudiation, meaning that the signer cannot successfully claim they did not sign a message, while also claiming their private key remains secret. Some digital signature algorithms are RSA-based signature schemes, DSA and its elliptic curve variant ECDSA, ElGamal signature scheme as the predecessor to DSA [5], and variants Schnorr signature [6] and Pointcheval-Stern signature algorithm [7]. In this thesis we use two main methods: RSA (Rivest-Shamir-Adleman) and ECDSA (Elliptic Curve Digital Signature Algorithm).

A lot of multiple digital signatures have been proposed in recent years. The security of these schemes is based on the difficulty of solving the factoring problem and the discrete logarithm problem. In this section, we compare them in terms of properties and efficiency. In the Introduction, some issues and challenges for multiple digital signatures are discussed and then addressed in the design of multiple digital signatures. These are also the properties [8] of multiple digital signatures. We compare them as follows:

• [1]    Only a valid signer can sign multiple electronic documents. All schemes can meet this property. If the signer has his/her private key, he/she can do that.

• [2]    No one can forge the multiple digital signatures. In these schemes, it is seen that only Hwang's BV- DSA, Hwang's BV-RSA, and Shao's scheme can meet this property. The multiple digital signatures of their scheme cannot be forged to make false batch verification valid.

• [3]    Any verifier can batch verify the validity of the multiple digital signatures .All schemes can meet this property. If the verifier has the signer's public key, he/she can batch verify the correctness of the multiple digital signatures which needs only single verification.

• [4]    It should achieve integrity. All schemes can meet this property. An attacker should not be able to substitute false documents for legitimate ones because he/she is not aware of the private key of the signer. Only the signer can generate digital signatures for particular documents.

• [5]    It should achieve non-repudiation. If the multiple digital signatures can be forged by a sender, it cannot meet this property because the sender can deny that he/she signed these multiple digital signatures. Therefore, only Hwang's BV- DSA, Hwang's BV-RSA, and Shao's scheme can meet this property [9].

• [6]    It should be able to detect forged multiple digital signatures efficiently. Most of these schemes cannot meet this property. Only Changchien et al.'s scheme can meet this property [10]. When the multiple digital signatures are forged, the verifier can detect these forged multiple digital signatures efficiently.

One way of dealing with the challenges of electronic signatures is to build trusted legal infrastructures. The notion of legal infrastructure [11] may be explained as those parts of a legal system that form the basis and conditions for legal activities. Trust has become a common denominator for evaluation of IT applications. A somewhat deepened analysis of the trust concept shows that from a legal point of view it is necessary to differentiate between well-founded trust, un-founded trust, well-founded mistrust and un-founded mistrust.

Digital time stamping is used to calculate the time that took by user to complete the process. The digital time stamping certified the particular record at the particular time and shows the digital document when introduced and changed by the user [12]. The digital time stamping system raises the integrity of the digital signature system by supporting two features with it. One is, a digital time stamping systems do not rely on keys, or any other secret information. So, time-stamping system cannot be affected by the disclosure of a key. Second, digital timestamping certificates can be renewed so as to remain valid indefinitely.

After studying the various research papers the major issues regarding the attacks can be identified as:

• a.    Security Attacks

In this section we explore related work on security challenges in electronic document transmission. An integrated Internet and transmission network can be subject to many types of attacks. These attacks can be classified into two categories, Passive attacks and Active attacks.

• b.    Passive Attacks

A passive attack [13] does not disrupt proper operation of the network. The attacker snoops the data exchanged in the network without altering it. Here, the requirement of confidentiality can be violated if an attacker is also able to interpret the data gathered through snooping. Detection of passive attacks is very difficult since the operation of the network itself does not get affected. One way of preventing such problems is to use powerful encryption mechanisms to encrypt the data being transmitted, thereby making it impossible for eavesdroppers to obtain any useful information from the data overheard. Among the active type of attack snooping is the primary concern to defend. Snooping is unauthorized access to another person's data. It is similar to eavesdropping but is not necessarily limited to gaining access to data during its transmission. Snooping can include casual observance of an e-mail that appears on another's computer screen or watching what someone else is typing. More sophisticated snooping uses software programs to remotely monitor activity on a computer or network device. Malicious hackers (crackers) frequently use snooping techniques to monitor keystrokes, capture passwords and login information and to intercept e-mail and other private communications and data transmissions.

• c.    Active Attacks

An active attack [13] attempts to alter or destroy the data being exchanged in the network, thereby disrupting the normal functioning of the network. It can be classified into two categories external attacks and internal attacks. External attacks are carried out by nodes that do not belong to the network. These attacks can be prevented by using standard security mechanisms such as encryption techniques and firewalls. Internal attacks are carried out by compromised nodes that are actually part of the network. Since the attackers are already part of the network as authorized nodes, internal attacks are more severe and difficult to detect when compared to external attacks.

The types of attack which affects the security concerns of the system are: denial of service, jamming, birthday attack, differential cryptanalysis, man-in-the-middle attack, linear cryptanalysis, timing attack, data modifications, sniffing, password cracking etc.

• IV.    SURVEY EXTRACTION

Two Elliptic Curves Digital Signature Algorithm: -Calculations over the real numbers are slow and inaccurate due to round-off error. Cryptographic applications require fast and precise arithmetic; thus elliptic curve groups over the finite fields of Fp and F2m are used in practice. Recall that the field Fp uses the numbers from 0 to p - 1, and computations end by taking the remainder on division by p. For example, in F23 the field is composed of integers from 0 to 22, and any operation within this field will result in an integer also between 0 and 22.

An elliptic curve with the underlying field of Fp can formed by choosing the variables a and b within the field of Fp. The elliptic curve includes all points (x, y), which satisfy the elliptic curve equation modulo p (where x and y are numbers in Fp). [14]

For example: “y2mod p = x3 + ax + b mod p “ has an underlying field of Fp if a and b are in Fp. If x3 + ax + b contains no repeating factors (or, equivalently, if 4a3 + 27b2 mod p is not 0), then the elliptic curve can be used to form a group. An elliptic curve group over Fp consists of the points on the corresponding elliptic curve, together with a special point O called the “point at infinity “. There are finitely many points on such an elliptic curve. As a very small example, consider an elliptic curve over the field F23. With a=1 and b=0, the elliptic curve equation is y2 = x3 + x. The point (9,5) satisfies this equation.

Since: y² mod p = x³ + x mod p

• a.    Calculations

25 mod 23 = 729 + 9 mod 23

25 mod 23 = 738 mod 23

• 2 = 2

The 23 points, which satisfy this equation, are: (0,0) (1,5) (1,18) (9,5) (9,18) (11,10) (11,13) (13,5) (13,18) (15,3) (15,20) (16,8) (16,15) (17,10) (17,13) (18,10) (18,13) (19,1) (19,22) (20,4) (20,19) (21,6) (21,17).

These points may be graphed as below. Note that there are two points for every x value. Even though the graph seems random, there is still symmetry about my = 11.5. Recall that elliptic curves over real numbers, there exists a negative point for each point, which is reflected through the x-axis. Over the field of F23, the negative components in the y-values are taken modulo 23, resulting in a positive number as a difference from 23. Here -P = (xp, (-YP Mod 23))

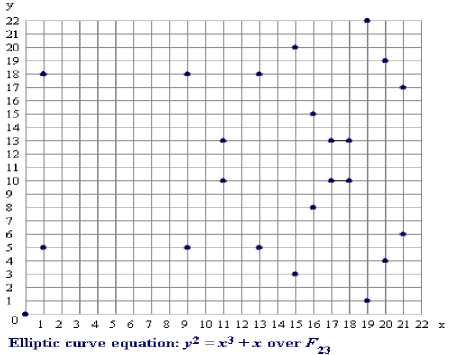
• b.    PHAL Algorithm

PHAL proposed in [15] is a hash algorithm designed as to improve the weaknesses of MD/SHA hash functions. Due to the proposed attacks motivates to design of a new hash functions where few elements of hash function are parameterized. This algorithm gives more secure and more flexible because of its iterative structure [13, 14].

PHAL consists of two mechanisms: new iteration schema and dedicated compression function. For PHAL hash algorithm parameter was the number of rounds. It is designed to be not only secure but also flexible [5].The main features are as follows:

• [1]    Number of rounds as a parameter was added to make this flexible function. The performed tests show that rounds must be greater than 1, but the authors suggest a number of round greater than 2.

• [2]    The number of bits hashed so far (counter) and random value (salt) were added to increase resistance of hash function to attacks against MD-type iteration structure.

• [3]    Instead of message expansion or message ordering, message modification technique with different message ordering for branches was used.

• [4]    Two branches are used in parallel. This means that PHAL family can be efficiently implemented in hardware and it is difficult to analyze both branches simultaneously.

PHAL family looks resistant against existing attacks, in particular against Wang at al.'s attacks [15].

In the existing system there are many are correlated factors should be considered: First is the complicate and flexible workflow in electronic government; second is the security of a digital signature algorithm; third is the speed problem of signing and verifying in a digital signature. Too much emphasis on security of digital signature theory previously, such as using complex signing scheme or increasing computing size in order to enhance security, while ignoring practicality. In practical application, security is often influenced by machines operating speed. And transmitting speed is a big bottleneck especially in a network environment [16]. Therefore to simplify operation should be a problem solved urgently under the premise of how to ensure safety.

In some situations, public-key cryptography is not necessary and secret-key cryptography alone is sufficient. These include environments where secure secret key distribution can take place, for example, by users meeting in private. It also includes environments where a single authority knows and manages all the keys, for example, a closed banking system. Since the authority knows everyone's keys already, there is not much advantage for some to be "public" and others to be "private." Note, however, that such a system may become impractical if the number of users becomes large; there are not necessarily any such limitations in a public-key system.

Small encryption exponent: If you use a small exponent like e=3 and send the same message to different recipients and just use the RSA algorithm without adding random padding to the message, then an eavesdropper could recover the plaintext [17]

Using the same key for encryption and signing: Given that the underlying mathematics is the same for encryption and signing, only in reverse, if an attacker can convince a key holder to sign an unformatted encrypted message using the same key then she gets the original [17].

• V. PROPOSED ECDSA APPROACH

This prototype secures the documents from replacement attacks. The ECDSA provides more security and less computation time. The Elliptic curve cryptography is an important branch of public key cryptography based on the elliptic curve and finite fields. In this prototype we use 3DES algorithm for the document encryption and to send a secret key (symmetric key) and for digital signature we use the ECDSA algorithm. To measure the time during the process we apply digital time stamping. Hash Function is used to generate the hash values. During the process we all assume that sender public key (Ka1) and receiver public key (Kb1) both known the public keys of each other. But the private keys of both sender (Ka2) and receiver (Kb2) are private to each. The transmitting process in the prototype is shown by the dotted line. The steps in this prototype are as follows:

STEP-1: In this prototype, PHAL function uses the electronic document as the input and generates the PHAL value of the document. This value is compared with the ECDSA signature verifying process. Then ECDSA use the private key (Ka2) of sender to sign the PHAL value and digital timestamp. At that moment, 3DES encrypt the document and produces cipher text.

At that moment, the secret key will be encrypted using public key (Kb2) of receiver by ECDSA. Then generate the cipher block (a small light rectangular in the right hand of Fig.1.). The cipher text and digital signature are sent from sender to receiver as shown in Figure 1.2.

STEP-2: At the receiver end the cipher text and digital signature are abstracted. The digital signature is verified by sender public key Ka2. It produces PHAL value and digital timestamp. To verify digital signature and sending secret key from sender to receiver, PHAL value will be signed by ECDSA by receiver private key Kb1 and then transmit feedback to the sender.

STEP-3: The sender verifies the digital signature using receiver private key (kb2) after receiving from the receiver. It is shown as a small dark rectangular in the left hand on figure 1.2. Then the sender can get a PHAL value which must be compared with the step 1’s PHAL value. And if the two PHAL values are identical with each other then the cipher block in the first step of the prototype will be transmitted to the receiver.

STEP-4: Then the cipher text is decrypted by ECDSA using receiver private key (Kb2). After decrypting the cipher block, the receiver must obtain a secret key which used for decrypting the cipher block using 3DES. Then the document obtained to the receiver.

STEP-5: The document obtained from previous step should be processed by PHAL function that produces PHAL value. The receiver can accept the document only if both PHAL values (one of sender and second to recover) are identical and digital timestamp is accurate by comparing these PHAL values and at the same time check for the digital timestamp obtained from step 2.

The digital signature prototype used in this paper ensures the highest security by using the combination of symmetric and asymmetric cryptography. The structure of the proposed prototype is shown in the figure:

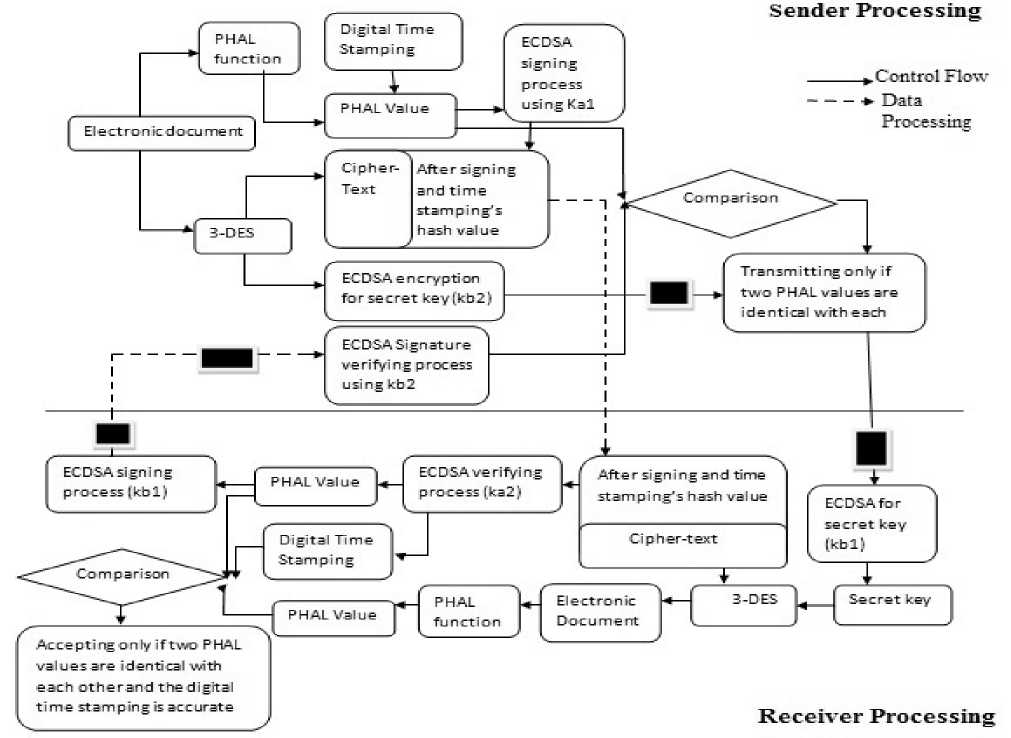
Figure 1: Proposed ECDSA approach

Prototype Structure

ECDSA Algorithm

An entity A’s key pair is associated with a particular set of EC domain parameters D= (q, FR, a, b, G, n, h). E is an elliptic curve defined over Fq, and P is a point of prime order and in E (Fq), q is a prime.

Each entity A does the following:

• [1]    Select a random integer d in the interval [1, n- 1].

• [2]    Compute Q = dP.

• [3]    A’s public key is Q, A’s private key is d.

To sign a message m, an entity A with domain parameters D= (q,FR, a, b, G, n, h) does the following:

• [1]    Select a random or pseudorandom integer k in the interval (1, n-1).

• [2]    Compute k*P =x1, y1 and r= x1 mod n (where x1 is regarded as an integer between 0 and q-1). If r= 0 then go back to step 1.

• [3]    Compute k-1mod n.

• [4]    Compute s= k-1 {h (m) + dr} mod n, where h is the Secure Hash Algorithm (SHA-1). If s = 0, then go back to step 1.

• [5]    The signature for the message m is the pair of integers (r, s).

• a. Signature Verification:

• [1]    To verify A’s signature (r, s) on m, B obtains an authenticated copy of A’s domain parameters D = (q, FR, a, b, G, n, h) and public key Q and do the following:

• [2]    Verify that r and s are integers in the interval (1, n-1).

• [3]  Compute w = s-1mod n and h (m).

• [4]    Compute u1 = h(m)w mod n and u2 = r*w mod n.

• [5]    Compute u1P + u2Q = (x0, y0) and v= x0 mod n.

• [6]    Accept the signature if and only if v = are.

• VI. CONCLUSION

  In this paper, various research issues and the related work to solve these issues was described. Generally, there are no of prototypes used for encryption and authenticity which are applicable to e-mail, electronic government environment. The standard approach is RSA for encryption and authentication that use different key size. The performance complexity of RSA is much as other encryption methods like ECDSA. The proposed prototype increases the efficiency and reduces computation time for encryption and authentication of electronic document using these methods in the data transmission environment. The execution time for signature verification is a lot shorter for RSA than for ECDSA whereas the execution time for RSA signature generation is a lot longer than those of ECDSA. The difference becomes even more dramatic as the greatest increase in RSA key sizes leads to an even greater increase in computational cost. So going from 1024-bit RSA key to 3072-bit RSA key requires about 27 times (3³) as much computation while ECC would only increase the computational cost by just over 4 times (1.6³).

FUTURE WORK

The other problem that can be faced in the prototype may be that the verification process of digital signature ECDSA look slow as compare to the RSA algorithm. But the signing process takes less time as compared to other algorithms. ECDSA use less key size and give the security of the same level of other algorithmic as RSA. So, next we try to reduce the time in verification of the digital signature in this prototype.

ACKNOWLEDGEMENT