A Novel Skull Stripping and Enhancement Algorithm for the Improved Brain Tumor Segmentation using Mathematical Morphology

Published Online July 2016 in MECS DOI: 10.5815/ijigsp.2016.07.07

Human brain is the most important and highly organized structure of human body. It coordinates and controls all the complex activities in the body. Brain and spinal cord makes the central nervous system (CNS). The average weight of human brain is about 3 pounds and is made up of more than 100 billion neurons. Human brain is made up of two types of tissues- gray matter and white matter. Gray matter contains unmyelinated neurons, most of which are interneurons. White matter is made up of bundles of long-range myelinated neurons. Brain and spinal cord baths in a particular type of fluid called cerebrospinal fluid (CSF). CSF is responsible for the protection of brain which helps to cushion any physical blows to the head. The brain is covered by a three layered structure named as Meninges. The inner layer of meninges is called pia mater, which is closest to the brain. The middle layer is called arachnoid. The outermost layer of meninges is called dura matter. Human brain is protected with a strong covering called as skull, which is made up of several bones [1- 3].

Brain tumor is the abnormal growth of cells in the brain or the membranes surrounding the brain. There are about more than 100 different types of brain tumors discovered [4]. Diagnosing of brain tumor is a challenging task since the anatomical structure of brain is very complex. Recently there are many types of medical imaging modalities available for the diagnosing purposes.

Medical imaging is the process of representing internal structure of human body for various clinical purposes such as medical procedures, diagnosing, surgery planning, and study of normal and abnormal parts etc. The concept of medical imaging was invented by W. C. Rontgen in 1895. He accidently discovered the X-rays, which helps to picturize the internal parts of human body in different shades of black and white [5]. After the invention of X-Rays, different anatomical and functional medical imaging modalities are emerged for medical imaging. MRI is one of the commonly used methods for brain imaging. MRI works on the basis of principle of nuclear magnetic resonance (NMR). It is a non-invasive imaging method and mainly used for the representation of soft tissues. The main advantage of MRI over other imaging modalities is that it does not emit any harmful radiations to the human body [6].

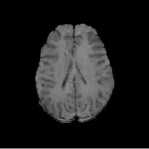
Figure. 1 represents an example of MR axial plane image of human brain. Though skull is an important part of human brain, it is not required for the analysis purposes [7]. So we need to remove the skull and other non-cerebral structures from MR brain images. That is, we need to extract the non-cerebral parts such as skull, Cerebrospinal Fluid (CSF) and Meninges. Skull stripping is an important pre-processing stage in the analysis of MR images. More accurate skull stripping algorithm reduces the probability of misclassification of abnormal tissues [8]. Here we proposes a novel algorithm for the skull stripping based on the technology of mathematical morphology.

One of the main problems associated with the MR images is its low contrast. It is due to the large amount of water content present in the human body. For the better visual quality, we need to increase the magnetic power of the MRI machine. But it is harmful to the human body. The other solution is to use some efficient algorithms for the contrast enhancement [9]. In this paper we proposes an efficient method for the contrast enhancement of MRI brain images based on the idea of mathematical morphology.

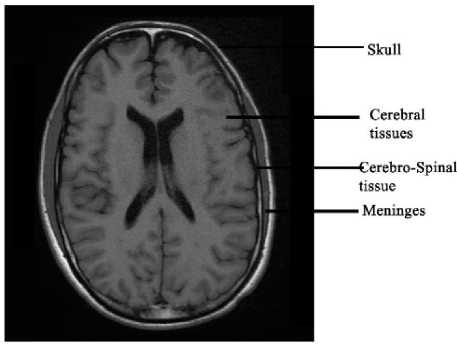
Fig.1. Axial Plane of Human Brain

The rest of the paper is organized as follows. Next section describes the literature survey. Section III presents the materials and methods used for this work. Fourth section covers the experimental results and discussions. And finally last section includes the conclusions and future enhancements.

• II.    Related Works

Brain imaging is a widely used method for detecting many abnormalities such as tumor, stroke, paralysis, Alzheimer's etc. MRI is one of the most efficient methods for brain scanning. The main problem related with MRI brain images is the presence of skull in the images. For the accurate segmentation of brain tissues, skull must be removed initially. Many methods are proposed for the extraction of brain portion from the MR brain images. F. Segonne et al. proposed an efficient method for the skull stripping of MR brain images based on a hybrid approach of watershed algorithm and deformable surface models [10]. They used the advantage of robustness of the watershed algorithm and the surface information availability advantage of the deformable surface models. Watershed algorithm is used to build an initial approximation of the brain and surface deformation method produces accurate skull stripped images. Finally they compared the results with other publicly available skull stripping tools.

Juan Eugenio Iglesias et al. introduced a robust, learning based brain extraction system (ROBEST) for the skull stripping from MR brain images [12]. In this method they combined a discriminative model called random forest classifier and a generative model called point distribution model for the skull stripping. Random forest classifier is used to detect the brain boundary and the point distribution model is used to ensure the result is plausible. Finally they proved that their ROBEST method produced more prominent result than the other well-known skull stripping methods. Francisco J. Galdames et al. proposed another efficient method for the skull stripping based on deformable models and histogram analysis. Their method is called Simplex Mesh and Histogram Analysis Skull Stripping (SMHASS) [13]. They applied a pre-processing method for finding the optimal starting point for the deformation.

Audrey H. Zhuang et al. implemented a mathematical algorithm for the skull stripping on the basis of model based level set (MLS) [14]. The level set method is used to evolve an active curve. The evolution of active curve controlled by two terms in the level set equation. One is developed from the mean curvature of the curve and the second one is designed to model the intensity properties of the cortex in MR images. Orazio Gambino et al. proposed an automatic algorithm for the skull stripping using morphological operators and fuzzy c-means algorithm [15]. Morphological opening operator is used to separate the brain region from the non-brain part. Fuzzy c-means algorithm is used to identify the background and the foreground of each transversal slice. Finally they compared the results with those obtained using the MRIcro software. Dwarikanath Mahapatra suggested a novel technique for the skull stripping of MR brain images using the prior shape information [16]. The prior shape information is computed from a set of labeled training images.

Mathematical morphology is the most commonly used method for skull stripping from MR brain images. In the literature we can see many methods for the separation brain and non-brain tissues based on the concept of mathematical morphology [17-20]. One of the main problems associated with these methods is that it may not work with the different MRI sequences. In this work we proposed an efficient method for the skull stripping on the basis of mathematical morphology, which is compatible with different MRI sequences such as T1, T2, FLAIR, and DWI.

Another important disadvantage associated with the MRI is that it produces low contrast images. For accurate diagnosing, finer details in the image should be visible. Therefore contrast enhancement is an important preprocessing step in the area of brain image analysis [21]. In the literature we can see many methods for the contrast enhancement of MR brain images. Most of the methods are based on histogram equalization [22]. Pratik Vinayak Oak et al. implemented and compared various histogram equalization methods for the contrast enhancements of MR brain images [23]. They implemented conventional histogram equalization (HE), bi-histogram equalization (BHE) [24], modified bihistogram equalization (MBHE) [25], brightness preserving BHE (BBHE) [24], Adaptive histogram equalization (AHE) [26] and contrast limited adaptive histogram equalization (CLAHE) [27]. Finally they concluded that for the better result, selection of the enhancement algorithm should be consider the nature of the images also.

N Senthilkumaran and J Thimmiaraja applied a set of histogram equalization methods on MR brain images [28]. They implemented different histogram equalization methods-brightness preserving BHE (BBHE) [24], Recursive Mean-Separate Histogram Equalization (RMSHE) [29], Brightness Preserving Dynamic Histogram Equalization (BPDHE) [30], Dualistic SubImage Histogram Equalization (DSIHE) [31] and Minimum Mean Brightness Error Bi-Histogram Equalization (MMBEBHE) [32].

A. Djerouni et al. proposed an efficient method for the enhancement of MR brain images called Newtonian operator (NO) [33]. After the enhancement they performed segmentation operation using fuzzy clustering method. Their method can be considered as a convolution filter but presents the originality of the adaptive found of convolution mask coefficients. Experimental results shows that their method produces images with low noise susceptibility and the low contrast images are enhanced without over-smoothing the edges.

• III.    Materials and Methods

Image pre-processing is an important stage in the medical image processing applications. In medical images, a good pre-processing method will leads to the better segmentation results. So in order to obtain relevant and accurate segmentation results, we have to apply several pre-processing steps. In this paper we proposes two MR brain image pre-processing methods-skull stripping and contrast enhancement. Skull stripping is the process of removing non-brain tissues from the MR brain images. Image enhancement methods inquire about how to improve the visual appearance of images from Magnetic Resonance Image (MRI). Both pre-processing methods are worked on the basis of mathematical morphology. Figure. 2 represents the block diagram of the proposed pre-processing method.

• A.    MR Image Dataset

For the experimental purposes we have used a total of 120 samples of MRI brain images (30 T1 images, 30 T2

images, 30 FLAIR images and 30 DWI images). Images are provided by the Medical College hospital, Thrissur. All the images are taken from the 2D axial plane with the dimension of 512x512.

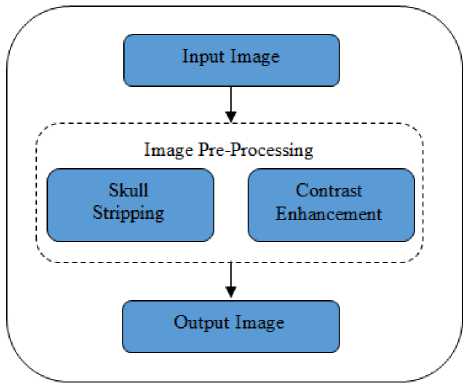
Fig.2. Block Diagram of the Proposed Work

• B.    Mathematical Morphology

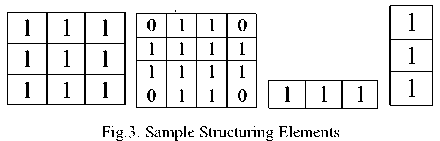
Mathematical morphology is a shape based tool used to extract the image components which are useful in the representation and description of shape, region, boundaries and convex hull [34]. The concept of mathematical morphology was introduced by Matheron and Serra at the Ecole des Mines in Paris [35]. Mathematical morphology is developed on the basis of set theory. It was initially used for the processing of binary images and later it is applied on the other type of images such as gray scale and color images. The main idea of mathematical morphology is to examine the morphological structure of an image using some small patterns at various locations on the image. These small patterns are called structuring element (SE). A structuring element is a small connected component of pixels. One can be used to extract the useful morphological information from the images by using the structuring elements. The shape and size of the structuring element varies between different applications. Any matrix can be used as a structuring element. There are many known structuring elements. Some of them are diamond, square, disc, horizontal line, vertical line, cross etc. Examples of structuring elements are given in the figure. 3.

Erosion and dilation are the two fundamental operations in mathematical morphology. Many other operations can be derived by using erosion and dilation. Opening and closing are the examples of such derived operations. Erosion is used to shrink the components of an image and dilation is used to expand the components.

Let A is a set (binary image) and S be the structuring element in Z² . Then the Erosion of A by the structuring element S , denoted by AƟS is the set of all pixels which S placed at that pixel is contained within A. In another way we can say that the Erosion of A by S is the set of all points z such that S , translated by z , is contained in A .

AƟS = {z ǀ (S) z ⊆ A} (1)

Erosion shrinks or thins the shape of an object. It is also used to exclude the small unwanted objects from the given image.

Dilation of A by S in Z² , denoted by A ⊕ S. Dilation of A by the structuring element S the set of all displacements z , such that ^̂ and A overlap by at least one element.

A⊕S= {zǀ ( ̂) z ⋂A≠ ø} (2)

Dilation is used for growing or thickening an image. It is also used to highlight the small objects in an image.

Opening and Closing are the other two operations in the mathematical morphology. Opening operation makes the contour of an object smoothened and break the narrow lines. Similarly closing operation also smoothens the contours, but it usually eliminates discontinuity and small gaps between the objects. Opening operation is denoted by A○S and closing operation is denoted by A•S , where A is the input image and S is the structuring element. In opening erosion is performed followed by dilation and in closing dilation is performed followed by erosion.

Opening , A○S = (AƟS) ⊕ S (3)

Closing , A•S = (A ⊕ S) ƟS (4)

Another important idea used in the mathematical morphology is morphological reconstruction. Using morphological reconstruction we can extract some connected components of an image, which are marked in the image. Morphological reconstruction can be implemented by applying series of dilation operations, until the edge of the marker image fits under a second image, which is called the mask image.

• C.    Skull Stripping

Automatic skull stripping from MR brain images is one of the important phase in the neuro-image analysis. The accuracy of the skull stripping algorithm affects many applications such as tumor segmentation, cortical surface reconstruction, pre-surgical planning etc. It is the process of removing non-cerebral tissues such as skull, meninges and eyeball from the MR brain images. In this paper we proposes an automatic skull stripping method based on mathematical morphology.

Working of the skull stripping algorithm is detailed below. The input MR brain image is binarized using Otsu’s method [36]. Otsu’s method finds the threshold that minimizes within-class variance between two different classes. From the binarized image, largest connected component is found. Brain part will be the largest connected component in the image. The largest connected component is then dilated with a 3x3 square structuring element so as to preserve minute brain information in the output image. The holes in the resultant image is filled to make the brain a complete connected component. The resulting pixels are superimposed with the input image for getting the skull stripped image.

The pseudo-code of the skull stripping algorithm is given below. Input of the algorithm is MR brain image, im and output is the skull stripped image, img _{stripped .}

Algorithm 1	: Skull Stripping
Input	: MR Brain Image (Im)
Output	: Skull Stripped Image (Im s!,ipped)

Im G Input MR Brain Image

Im ъ-п G Otsu (Im)

Con G Largest Connected Component (Im ы,)

Con' G Con © SEi repeat

Con’к ^-Соп’к-i ® SEif^Im1

until

Con’к— Con’K-i

Im dripped ^" Superimpose (Con' ^

• D.    Contrast Enhancement

MR images are usually low contrast images. To make the images more visual, a hardware or software level image enhancement should be performed. Contrast enhancement is the process of improving visual components of an image so that it is suitable for certain applications. It helps to enhance the clarity of the image, which makes further analysis becomes easier and faster. Enhancement also explores the hidden features in the image. One of the commonly used methods for MR image enhancement is histogram equalization. The main problem associated with the histogram equalization is that it may not be works with all sequence of MR images. Here we proposes an efficient method for the contrast enhancement based on mathematical morphology. Since the structure of the brain is round shaped, here we used a disc structuring element for morphological operations.

Working of contrast enhancement algorithm is explained as follows. Initially algorithm finds the complement of given skull stripped MR brain image. Closing operation is applied on the complemented image using disk structuring element. Then calculates the complement of previous result. Later the mathematical operation finds the difference between the original image and resultant image. Finally, original image is added with the differenced image to get the final contrast enhanced image.

The pseudo-code of the contrast enhancement algorithm is given below. Input of the algorithm is skull stripped MR brain image, Im stripped and output is the enhanced image, Img enhanced .

Algorithm 2: Contrast Enhancement

Input : Skull stripped Image (Im stripped) Output : Contrast Enhanced Image (Img entered)

Img ^- Skull stripped Image

Img^c £■ (Z-l) —Img

C <- Img1 * SE;

D t- (Z-l)-C

Imgdtf ^~ Img-D

Img en^ed <- Img + Img ^

tissue

TN = Pixels that are correctly classified as non-brain tissue

FN = Pixels that are incorrectly classified as non-brain tissue

IV. Results and Discussions

Skull stripping and contrast enhancement are the two important pre-processing stages in tumor characterization. It helps to avoid non brain information from the input image and to enhance the contrast of the image. Figure. 4-7 shows the results of the proposed work on different MR Brain Image sequences. The algorithms are applied on the various image sequences of brain MRI. First column represents the input MR images, second column represents the skull stripped images and last column includes the contrast enhanced images.

Result of the skull stripping algorithm is compared with the manually marked ground truth using two standard similarity coefficients Dice [37] and Jaccard [38]. Skull stripping is carried out by using Matlab toolkit and the ground truth is created with the help of ITK Snap tool [39]. It is an open source software that contains innovative tools for manual outlining and quality control. The performance of the skull stripping algorithm is given in the table. 1. The false positive rate (FPR) and false negative rate (FNR) are also included in the table. FPR shows the degree of under segmentation and FNR shows degree of over segmentation. Average performance using Dice coefficient is 94.33 and using Jaccard coefficient is 90.88. False positive rate is 0.0061 and false negative rate is 0.0423.

Table 1. Performance of Skull Stripping Algorithm

	Dice	Jaccard	FPR	FNR
DWI	96.18	92.12	0.0054	0.0291
FLAIR	95.61	91.33	0.0059	0.0328
T1	93.08	90.13	0.0063	0.0481
T2	92.45	89.95	0.0069	0.0594
Average Performance	94.33	90.88	0.0061	0.0423

The efficiency of the contrast enhancement algorithm is calculated using some standard measures such as Signal to Noise ratio (SNR), Peak signal to Noise Ratio (PSNR), Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) [40]. The performance of the enhancement algorithm is given in the table. 2. Average value of Signal to noise ratio is 23.67, peak signal to noise ratio is 27.10, root mean square is 11.52, and mean absolute error is 5.01.

SNR= 10. log10 [

PSNR = 10. log10 [

=

√ ^∑

_{∑     ∑     [} r ( X ,У)]^2

_{∑      [ (} X ,У) -t ( X ,У)]^2

( ( X , У ))

_{∑      ∑      [} г ( X , У )^( , У )]

․ тгу

_{∑     [ (}у ,У) -t ( х , У )]^2

․

]

]

А ( s ) ∩ А ( G ) | Dice Coefficient = | А ( S )| +| А ( G ) |	(5)
_   ТР	(6)
TP+FP+FN
Jaccard Coefficient = - ( - ) ⋂ 4 ()	(7)
Л(5)U Л( G )
_   2ТР	(8)
2TP+FP+FN
FP FPR =	(9)
TN+FP
FN FNR = TP+FN	(10)

МАЕ _{∑    ∑    | (} ^ ^, у ⁾ ^ ⁽ ^ ^, У )|

.

Table 2. Performance of Contrast Enhancement Algorithm

	SNR	PSNR	RMSE	MAE
DWI	24.58	27.47	10.79	4.83
FLAIR	23.79	29.15	11.12	4.99
T1	23.33	26.61	11.49	5.03
T2	22.97	25.18	12.67	5.19
Average Performance	23.67	27.10	11.52	5.01

A (S) = Pixels calculated using the proposed algorithm A (G) = Pixels obtained from the ground truth TP = Pixels that are correctly classified as brain tissue FP = Pixels that are incorrectly classified as brain

The experimental results show that the proposed skull stripping and contrast enhancement algorithm can be effectively used for various medical image analysis applications such as tumor segmentation, classification and characterization.

DWI Samples

T1 Samples

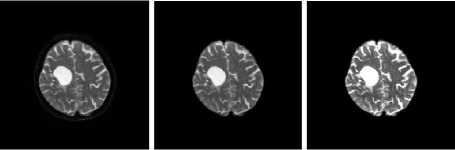
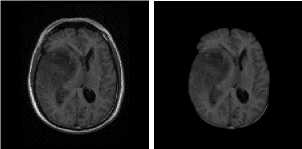
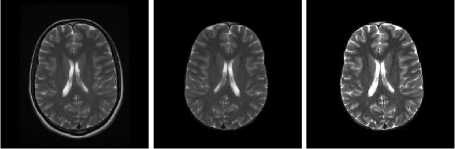
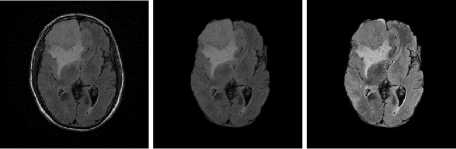
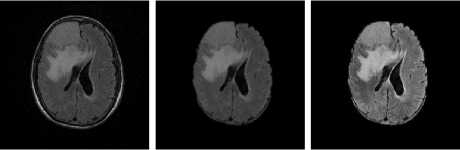
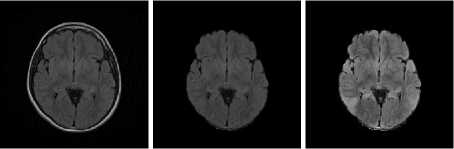
(a) Input Images    (b) Skull Stripped (c) Enhanced Image

Fig.4. Result on DWI Image Samples

(a) Input Images     (b) Skull Stripped

(c) Enhanced Image

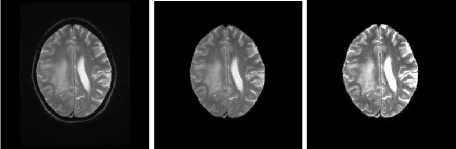
Fig.6. Result on T1 Image Samples

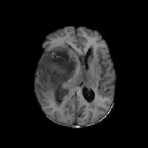
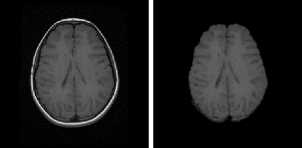
FLAIR Samples

T2 Samples

(a) Input Images     (b) Skull Stripped (c) Enhanced Image

Fig.5. Result on FLAIR Image Samples

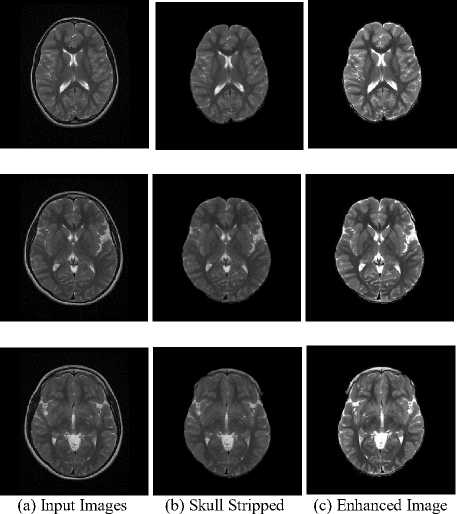
Fig.7. Result on T2 Image Samples

• V. Conclusions

Pre-processing is an important stage in the image processing especially in the case of medical image segmentation applications. An efficient image preprocessing algorithm will increase accuracy of the segmentation algorithms and reduces misclassification. In this paper we propose an efficient method for preprocessing of MR brain images based on mathematical morphological operations. Skull stripping and contrast enhancement are the two pre-processing methods proposed in this paper. Experimental results show that these two pre-processing steps increase the performance of tumor segmentation algorithms. The proposed work can be effectively applied on different MR Image sequences such as DWI, FLAIR, T1 and T2. Now the algorithm worked on the 2D MR Brain images. In the future we can evolve the algorithms for the preprocessing of 3D MR Brain images.