A parameterization algorithm for the Vaganov–Shashkin model of seasonal growth and tree-ring formation

The Vaganov- Shashkin model of seasonal growth and tree-ring formation [1–3] (hereinafter referred to as VS-model) describes the influence of climatic conditions on the cellular structure of annual rings. The main destination of the model consists in using it as a tool permitting any individual or generalized tree-ring chronology (TRC) during a set of years with available meteorological station data (see below description of the VS-model input): 1) extracting the climate-driven component of the TRC under consideration; 2) pointing, if modeling quality of the involved TRC by the VS-model is satisfactory, for arbitrary day of the given years set, what of two factors – air temperature or precipitation – had limited the growth of woody plant which corresponds to the TRC. TRC is a time series of values of some numerical characteristic of tree/trees of this TRC [4].

The main destination of the VS-model, in particular, is that it makes possible to use it as a quality tester for individual and generalized TRCs which will be used as mediators, carrying information about climatic data [2]. A TRC is considered to be suitable for using for the purpose of a mediator for carrying climatic information if and only if its climate-driven component had been extracted by the VS-model conforms with the TRC satisfactorily enough.

The VS-model is a deterministic dynamic simulation model. Its input data consist of two blocks. The first block is the climatic data of daily resolution at air temperature, precipitation, and doses of solar radiation coming down to the Earth’s surface. The data of this block can refer to an arbitrary set of years, which does not have to be continuous. However, climatic data per year must not contain missing values.

The second block is a set of the VS-model’s parameter values. The model has 42 parameters. All parameters, except two, are real single-valued variables and three parameters are integer single-valued variables. Two parameters are vectors of equal dimension. One of the vectors contains real single-valued variables, the second – boolean single-valued variables. The dimension of the vectors is a parameter of the VS-model.

The value of each parameter provides the VS-model with information either on the actual tree or on its site. The VS-model has 10 options. A set of option values defines the VS-model variant which will be used for modeling. The options of the VS-model define a collection of its modules being run under modeling, calculating accuracy under modeling, etc.

The output of the VS-model consists of two blocks. The data of the first block consists of numerical characteristics reflecting the dynamics in time, the time step of whose tracking does not exceed one day – for some processes taking place in the modeled tree and its modeled site (soil moisture, value of tree transpiration, number of cambial cells, etc). The contents of this block depend on the used set of the VS-model option values.

The second output block of the VS-model is a model of TRC. The VS-model supposes the actual individual TRC for being modeled to be a time series of values either of width of a formed annual ring or of number of wood cells in such a ring. The VS-model supposes all individual TRC are used for the construction of an actual generalized TRC to be such a one described above. For each year of the VS-model, the climatic input of the second block contains the value of modeled TRC.

This value does not have any units if a generalized TRC has been modeled. If an individual TRC has been modeled, this value either does not have any units or is number of wood cells in an annual ring (variants, taking place are determined by the used set of the VS-model options values).

A parameterization problem and approach to its solution for the VS-model. In the field of mathematical modeling the term “parameterization” is usually understood as either an activity on describing some process/phenomenon by means of a finite number of parameters, i. e. the creation of a parametric mathematical model of this process/phenomenon, or choosing certain values of parameters of a parametric mathematical model that were already created. In the article the term is being understood according to the second interpretation.

To process the VS-model it is necessary to have certain numerical values of its parameters. Sets of these values must have the necessary internal structures that are specified by interrelations between parameters of the VS-model and by ranges of parameter values. Meaning, many parameters, the VS-model structure, semantics of its output components, and specific context in which modeling is performed determine the mentioned interrelations, and value ranges. As a rule, the checking a set of values of the VS-model parameters for the presence of the necessary internal structure in it requires an analysis of the VS-model output that corresponds to this set.

In an attempt to set certain values to the model’s parameters to realize the modeling, it often happens that the available information is not enough for the identification of exact values for some parameters. For such parameters it is possible to provide only a qualitative assessment of their values, for example, by means of determining the boundaries in which the values of these parameters lie. In addition to a number of properties of some the VS-model’s parameters, it complicates the empirical measurement of the values and makes the exact value conception for these parameters meaningless. It has as a consequence in a situation when for each parameter of the VS-model, the range of its values was known, and for some parameters their specific numerical values are known.

The parameterization problem for the VS-model is a problem of choosing values of those parameters, for which only the ranges of their values are known. The choice has to be realized within these ranges in such a way that the derived set of values of all the VS-model parameters has the necessary internal structure. How do we realize this choice? What should one be guided by to realize the choice? These two questions are the essence of the parameterization problem. The parameterization problem of an existing mathematical model is a problem of choosing the model input data in conditions of insufficient information.

There are different approaches used in the practice of solving the parameterization problem of a parametric mathematical model [5]. A solution to the parameterization problem for the VS-model, presented below, uses the existing arbitrariness in choosing values of parameters, for which information is necessary for determining their exact values is absent, purposively. Values of the parameters are selected, which conform to the researcher’s objective formalized in a form of reaching the optimum of an objective function in the optimal, over the domain of definition of the objective function, way (conform in the optimal way). The proposed solution to the parameterization problem for the VS-model can be applied only in cases when entity for being modeled is available, in particular, under using the VS-model according to its main destination.

A concept of difference criterion between actual TRC and its model. Introducing the concept “difference criterion between actual TRC and its model”, being significant out of the context of the VS-model parameterization problem, to state the solution being proposed in this article to the latter problem. The actual TRC is a TRC for being modeled. The difference criterion is a real single-valued nonnegative function of two arguments, denote it by DC(trCr, mCr), that is defined over a set of pairs of real vectors of equal dimension with nonnegative components. The dimension of the vectors is the power of set Yrs. The set Yrs is the intersection of two sets – set of years, which the modeling has been performed for, and set of those years, which values of the actual TRC are available for.

The first argument is that trCr must be a vector of values, relating to the years Yrs , of the actual TRC, which are situated in the vector in increasing order of the years. The second argument must be mCr a vector of respective values of the TRC modeled by the VS-model.

A value of the difference criterion characterizes the remoteness of the TRC model, obtained by means of the VS-model, from this actual TRC. Given a fixed actual TRC, a smaller value of the difference criterion corresponds to a better model of this TRC. A difference criterion introduces the relation of equivalence on a set of models of the certain fixed TRC and orders the equivalence classes linearly.

A difference criterion between actual TRC and its model must have two additional properties: symmetry property on its domain of definition and reflexive property ( trCr = mCr implies DC ( trCr , mCr ) = 0). These two properties are not imposed on the difference criterion between actual individual TRC and its model since semantics of the actual TRC values (including units of measurement) coincides with semantics of values of the TRC model, obtained by means of the VS-model, guaranteed for generalized TRCs only.

The necessary properties of a difference criterion do not guarantee its continuity. Multivalued difference criteria have not been considered in this article.

The testing and approbation of the parameterization algorithm for the VS-model, which is presented below, have been done with the following two difference criteria which are being offered for using as default difference criteria. Difference criterion DC ITRC between actual individual TRC and its model, and difference criterion DC GTRC between actual generalized TRC and its model are defined with formulas:

DC_{i trc} ( trCr, mCr ) = 1 - crln( trCr, mCr ) +

+ 1,25 ( 1 - sync( trCr, mCr ) ) 2 , DC _gtrc ( trCr, mCr ) = DC _itrc ( trCr, mCr ) +

+ 0,4 (max ItrCr - mCr I)2, i e Frs i where crln(trCr, mCr) and sync(trCr, mCr) are coefficients of Pearson’s correlation and of synchronism (coincidence) between vectors trCr and mCr, trCri (mCri) is a corresponding to the year i component of the vector trCr (mCr).

The selection of such difference criteria is conditioned by a desire: 1) to get calculated TRCs the most possible positive correlated with their respective actual TRCs;

• 2)    of not having small values of synchronism coefficient between actual TRC and its model; 3) of absence of serious visual differences between broken lines that represent an actual generalized TRC and its model. The difference criteria DC ITRC and DC GTRC have been tested on extensive data, are compatible with the parameterization algorithm for the VS-model (see below), and reflect the view of most researchers on concept of proximity of two TRCs.

The parameterization algorithm. Let us introduce definitions and denotations. Let p = ( p 1 , …, p n ) denote vector of the VS-model parameters used under modeling (PUuM). Vector p is uniquely defined by a set of the VS-model options values used under modeling. We denote that the numbers of these n parameters of the VS-model, which certain numerical values are known for, by i 1 , …, i k ; let c_{i 1} ,..., c_ik denote the certain numerical values known for these parameters. The range of values of the VS-model parameter i is denoted by [ a i ; b i ]. For the ease of exposition, it is supposed that a ij = b ij = c ij for j = 1, …, k .

Let us call the following subset of ( n – k ) a dimensional parallelepiped:

P = {p g Rn : ai < pi < bi for 1 < i < n} lying in Rn the optimization space S. S is defined by the condition: an element of P, considered as a set of values of the PUuM, belongs to S if and only if it has the necessary internal structure (see above). Call a set, belonging to S, of values of the PUuM a feasible. We consider S + 0. The structure of S is conditioned by the interrelations, used under modeling, between the PUuM. S resembles a rectangular piece of cheese. It is a typical situation: among 100 000 values of the continuous n-dimensional random variate uniformly distributed on P only one belongs to S.

Define the predicate function pFail(p ): P ^ {“TRUE”, “FALSE”} taking the logical value “TRUE” only if p t S . As a rule, for calculation of pFail ( p ) the VS-model output data obtained for the set p are necessary.

Let us call the quantity:

sup{ x g □ : VInpOpt1 VInpOpt2,

(|pi — pi21 < x ^ Q(Output1, Output2))} the accuracy along the i-th axis, 1 ≤ i ≤ n. Here InpOpt1 and InpOpt2 – are two collections of the VS-model input data and of values of its options, which differ only in values pi1 and pi2 of the i-th PUuM, Output1 and Output2 – the VS-model output data corresponding to InpOpt1 and InpOpt2 respectively. The predicate Q is true if and only if Output1 and Output2 differ from each other so little that this difference may be ignored and is considered to be negligible. Denote by hi an estimate, used under modeling, of the accuracy along the i-th axis.

We introduce S - a metric d : S x S ^ [0; + » ) defined as:

d ( x , y ) = max

1 <  i <  n

x ^- y , h_i

Selecting a metric on S is not a trivial problem. Such a metric is introduced in S since: 1) the optimization space has, generally speaking, different physical units of measurement along with different axes; 2) the constants h i corresponding to axes with equal physical units of measurement can be different; 3) it is a natural analog of the metric p „ on R ⁿ [6].

Let us state the parameterization algorithm for the VS-model. The proposed algorithm selects a set of values of the PUuM from the optimization space S ; the selected set provides the global minimum over S of the objective function F ( p ). The algorithm requires that F ( p ) is a real single-valued nonnegative function defined everywhere on S . The algorithm does not require any additional properties of F ( p ). The objective function is defined by a following equality:

F(p ) = DC ( trCr , mCr(p )), p g S , where mCr ( p ) is the vector of values, relating to the years Yrs , of the TRC model (see above) derived by using the VS-model with the set p of the PUuM values. The proposed parameterization algorithm for the VS-model is applicable with any difference criterion. It considers only those properties of the difference criterion being minimized by the one in which any difference criterion has necessarily.

The objective function F ( p ) and its domain of definition S are individual for every situation which the parameterization algorithm being stated is applied in. Investigating the problem of searching the global over S minimum of F ( p ) have shown that F ( p ) has more than one local minimum as a rule. Input and output algorithm data and its structure are presented in figure.

A zero-order method of multidimensional one-criterion search of global minimum, used by the parameterization algorithm, is a multistart method of a coordinate descent method [7]. The question of existence of a more effective method for solving a family of problems, searching the global over S minimum of F ( p ) is not considered in this article. The used coordinate descent method differs from the classical one in the following ways: 1) order of tracing coordinate axes of S is defined by a user; 2) a metric different from the Euclidean one is used on S ; 3) the used one-dimensional optimization method performs a search of a global optimum; 4) absence of requirement of F ( p ) being continuous, and complicated structure of S require a modification of the classical coordinate descent method.

Settings of the parameterization algorithm are a collection of six constants m , level , maxIter , ε, q , maxStart , and two vectors τ and wght . The algorithm uses the same values of its settings over a period of all its operations being performed. The following settings of the parameterization algorithm are being offered for using as its default settings: m = 3, level < inf p _{g s} F(p ), maxIter = 500, ε ≤ ( n – k )^–1, q = 1, maxStart = 1000, τ _i ≤ h_i ∙ min(1, ε) (1 ≤ i ≤ n ), wght j = 0 for j = i 1 , …, i k (default values of remaining n – k positive components of the vector wght are not noticed in the article). The oddness of m , and truth of inequality τ _i ≤ h_i ∙ ε, 1 ≤ i ≤ n , are necessary for correct functioning of the algorithm.

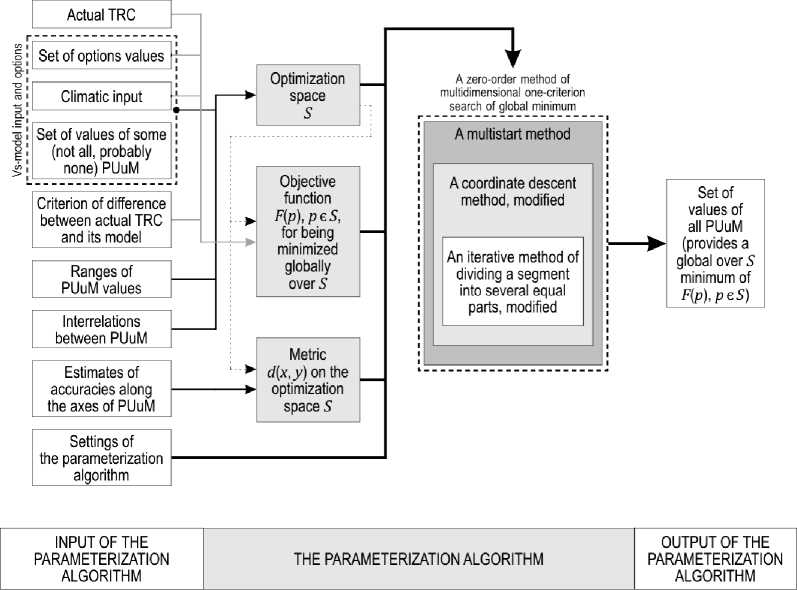
Structural scheme of the parameterization algorithm for the VS-model

The multistart method launches the coordinate descent method from maxStart starting points in S with the same settings. The least of maxStart local minima found is an estimate of a global minimum and is delivered as a result of the multistart method run. Starting points are generated in a random manner and are different values of the continuous n -dimensional random variate uniformly distributed on P .

The order of tracing the coordinate axes of S with the coordinate descent method is defined by the weights wght . Each iteration of the latter consists in performing one-dimensional minimizations along the coordinate axes of S that have positive weights; halting condition is checked at the end of the iteration. One-dimensional minimizations along the axes that have maximum weight are carried out in the first instance. Axes with equal positive weights are traced in the order induced by their numbers – the smaller the number, the earlier the minimization is made.

The minimization along axis i , 1 ≤ i ≤ n , means searching a global minimum of function f ( x ) = F (…, p i– 1 , x , p i+ 1 , …) of a real variable x on a set that lies inside the segment [ a i ; b i ] and which is specified by predicate function xFail ( x ) = pFail (…, p i– 1 , x , p i+ 1 , …). After having performed the search, a value x ^* at which global minimum of f ( x ) occurs is being written into the i -th coordinate of the current point p in S . In entering the first iteration, the current point p coincides with the starting one which has been selected by the multistart method. Coordinates of p with zero weights are not altered over a period of all operations being performed by the coordinate descent method.

The halting condition holds in case of truth of at least one of conditions: 1) number of iterations have reached a threshold maxIter ; 2) F ( p ) <  level , where p is a current point at the end of iteration (after executing all onedimensional minimizations of the iteration); 3) d ( p^N , p^N–i ) < ε for all i = 1, …, q ( N – the current iteration number, p ^j – current point in S at the end of iteration j , q and ε – positive constants); 4) d ( p^N , p^{N– 1}) = 0.

The one-dimensional minimizations along the coordinate axes of S are carried out by the method that is a modification of an iterative method of dividing segments into several equal parts [7]. During each iteration the method divides current segment into m equal parts and either makes one of them a current segment or completes the operation informing the user about the necessity to change the value m . The iterations stop when the value, on the current segment, of the function being minimized becomes less than the value level , or when the length of the current segment becomes less than the value δ defined before launching the method.

All one-dimensional minimizations along axis i , is carried out in the course of running the coordinate descent method, are performed with δ = τ i (1 ≤ i ≤ n ).

The realization and approbation of the parameterization algorithm. The parameterization algorithm for the VS-model is realized in programming language C++, using the means of the Standard C++ Library. Its textual code satisfies the C++03 standard (ISO/IEC 14882:2003). The executable code of the realization for a certain operating system can be derived without changing the textual code of the realization and is arranged as a dll-library (if the objective platform is an

OS of the Windows family) or a text-file (if the objective platform is an OS of the Unix family).

The main factors influencing the duration of parameterization for a certain TRC by means of the realization, being considered, of the parameterization algorithm are: 1) the set of values of the VS-model options used under modeling; 2) the power of the set of the years which modeling is performed on; 3) the interrelations between PUuM used under modeling; 4) the value of the quantity n – k and the lengths of the values ranges of those PUuM which specific numerical values are not known for; 5) the difference criterion used under parameterization; 6) the used settings of the parameterization algorithm; 7) hardware and software of a device carrying out the code of the parameterization algorithm realization. Varying any of these factors, one can get a significant change (of many times) of the duration of parameterization.

Using laptop Asus F3JP with dual core processor T5300 (maximum clock frequency of each core is 1.73 GHz), the parameterization of a TRC by using the realization of the parameterization algorithm usually lasts from several hours to several days.

The proposed parameterization algorithm for the VS-model was used at more than 700 different pairs (S, F(p)). Having performed these parameterizations as a consequence: 1) a number of statements about the VS-model, both the new and the previously formulated, are first confirmed by acomputing experiment; 2) a hypothesis about the relationship between the models of individual TRCs and the model of the generalized TRC (all the models are derived by using the VS-model with the same set of values of its options) is for the first time formulated and confirmed by a computing experiment; 3) the VS-model has been first used in full as the quality tester of individual and generalized TRCs which are going to be used in the role of mediators carrying climatic information; 4) several properties of the considered parameterization algorithm have been established. The successful approbation of the parameterization algorithm and its realization is due to these results.

The results obtained in this article are demanded mainly in dendroclimatology and dendrochronology, and in mathematical modeling of processes taking place in woody plants. The created parameterization algorithm and its realization: 1) significantly extend the range of situations in which using the VS-model is already realizable in practice; 2) allow the testing and analyzing of the model at a qualitatively new level; 3) allowing to solve in practice inverse problems of restoring certain growing conditions for woody plants via its existing TRC.