A Recursive Binary Tree Method for Age Classification of Child Faces

Published Online October 2016 in MECS DOI: 10.5815/ijmecs.2016.10.08

Biometric identifiers are the distinctive, measurable characteristics used to label and describe individuals [1]and are often categorized as physiological or behavioral characteristics [2]. Physiological characteristics are related to the shape of the body, examples include, but are not limited to, fingerprint, face recognition, DNA, Palm print, hand geometry, iris recognition, retina and odor/scent. Behavioral characteristics are related to the behavior of a person, including but not limited to: typing rhythm, gait, and voice. Biometric traits can also be classified as either soft or hard. Hard biometric features are those that uniquely identify an individual while the soft are those that do not uniquely identify persons but when used alongside the hard biometric features, could facilitate the recognition process [3]. Fig. 1 shows these different classification of biometric traits.

Facial age estimation is the task of labelling a face with its exact age or age range. Age fabrication occurs when an individual deliberately misrepresents his or her true age with the intent to garner privileges or status that would not otherwise be available to the individual. In West Africa countries, especially Nigeria, Age fraud or falsification has been rampant in the civil service, military and sports and generally on the Internet.

In the Nigerian Judicial Council, it was found that Justice Shadrach Nwanosike falsified his date of birth to postpone his retirement by some years. One of the best known examples of a footballer falsifying documentations is Cameroon's international football defender, Tobie Mimboe, who held several documents during the course of his career that indicated he became younger as time went by. Also, the Advertising Standards Authority conducted a survey that found that 83% of the 9 to 15 year olds whose Internet usage was monitored, registered on a social media site with a false age and this results in minors seeing inappropriate contents targeted towards adults. Age falsification is also prevalent in juvenile sports teams especially within the African football league; Under-17 football team, Under 23 football team etc.

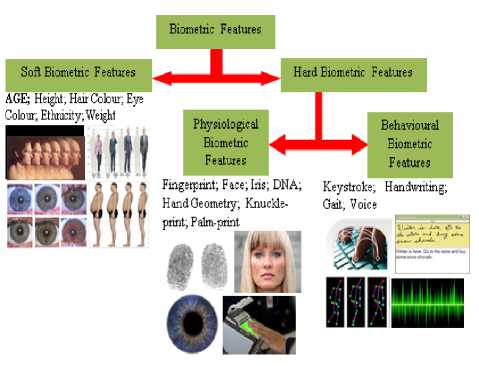
Fig.1. Classification of Biometric Features [38]

Listed above are some of the impetus for this work. Consequently, we propose a system for automatic age classification of humans within the age range of pre– teens (3 to 11 years) using still facial image captured under moderately controlled environment. Our proposed system is based on a binary tree classification approach for estimating the ages of individuals from their still facial image. We experimented our approach on the publicly available FG-NET [4] dataset and a locally collected dataset FAGE [5] which has been extended for the purpose of this study. Our experiments were carried out on portions of the dataset containing the stated age.

The rest of this paper is organized as follows; section II discusses related works, section III discusses the methodology of our proposed recursive binary tree, section IV discusses our experiments and the results and the conclusion of this write up is presented in section V.

• II.    Related Works

In recent years, there has been a growing interest in the Computer Vision, Image Processing and Pattern Recognition research communities to address the many problems related to facial aging such as: age estimation, appearance modeling, age-invariant face recognition/verification, etc. Based on the observation that facial shape variations are more observable in child faces while textural variations are more observable in adult faces, some works have employed a classification model to determine the age group of human faces – this includes the earliest research in the field [6]–[10].

Age estimation techniques were often based on shapebased cues and texture-based cues that were extracted from faces and they can be broadly classified as holistic features based approaches and local features based approaches. While local feature-based approaches used anthropometric distances extracted from different facial regions to estimate age, holistic approaches typically adopted subspace methods to reduce the dimensionality of faces and subsequently used regression techniques to estimate age from face images.

Some of the earliest works used holistic-based approaches in which facial features were extracted from the entire face [10]–[13], while other works [14]–[18] proposed using features which are localized within certain regions of the face instead of the global features obtained from the entire face.

More recent works have employed several approaches to age estimation by employing either a classification, regression or hybrid approach. Chang et al. in [19], [20] employed a ranking approach to age estimation by performing pairwise comparison of faces to determine who was older and arriving at an age estimate for such individual after several such comparisons. Cao et al. in [21] improved upon this intuition of age ranking by adding a set of consistent face image pairs to the ordinal pairs previously used. Thus, they were able to compare facial images of individuals with different and the same age using RankingSVM. The inferences obtained from the comparison were then used for age estimation. Onifade and Akinyemi [5], [22] were able to extend this notion to employ what they called ‘GroupWise’ age- ranking which is similar to the listwise ranking [23]–[25] of Information Retrieval and obviously an improvement over the pairwise comparison employed in previous works. Their result modelled the comparison of facial images across same and different ages while learning across different individual ageing patterns. Their result showed significant improvement even fr multi-racial age estimation. Some recent works have also employed variations of Support Vector Machine (SVM) for Regression which is also referred to as (SVR) [26]–[30].

In this work, we investigated the problem of age estimation using a classification approach – precisely, a binary classification method – to first separate adult faces from young faces and iteratively employed the same method to determine the ages of individual with ages less than 12 years. Although, the experiment covers a relatively small age range, we were able to demonstrate the performance of our proposed approach on a set of indigenous African faces, an area yet to be properly investigated in age estimation. Our intuition is that since ageing is affected by external factors such as weather and the condition of living, there is need to test age estimation algorithms on Africans who actually reside within the continent as opposed to Africans living in the diaspora as is obtainable in most popular facial ageing datasets such as MORPH [31].

• III.    Methodology

• A.    Overview of the Proposed Method

The performance of Facial image analysis systems is highly influenced by the learning algorithm employed, among other things. This therefore necessitates employing learning algorithms that are well suited to the problem at hand or tailoring them to be well-suited. Recent results in Pattern Recognition have shown that Support Vector Machine (SVM) classifiers often have superior recognition rates in comparison to other classification algorithms in facial age estimation. However, SVM was originally developed for binary decision problems, and its extension to multi-class problems is not so straightforward. How to effectively extend it for solving multiclass classification problem is still an on-going research. The popular methods for applying SVMs to multiclass classification problems usually decompose the multi-class problems into several two-class problems that can be addressed directly using several SVMs.

We propose a Binary Tree Architecture that uses SVMs for making the binary classification decisions at the nodes. The proposed classifier architecture takes advantage of the high classification accuracy of SVMs to repeatedly narrow down the age group to which a facial image belongs as it traverses the classification tree. This method uses multiple SVMs arranged in a binary tree structure and at each node, several SVMs are trained to improve the efficiency of the binary classification at each node of the tree. This step is repeated at every node until we get to the leaves of the classification tree which are age groups. At each level of the tree, an overlapping function is used to resolve conflicts and/or overlaps in age classification.

Our approach combines the advantages offered by Local Binary Pattern (LBP) invariance to monotonic gray-level changes and computational efficiency with the high classification accuracy of SVMs to obtain a suitable classification structure for facial images of toddlers and pre-teens (ages 3 – 11 years). In spite of the dominance of facial shape variation observable in the investigated age, the computational power of LBP proves to be of great help in discriminating texture features within the age group. Also, the incorporation of several trained classifiers in a single tree structure helps fine-tune the classification results and enhances the employment of SVM for multi-class classification. We present a general overview of our age estimation model in Fig. 2.

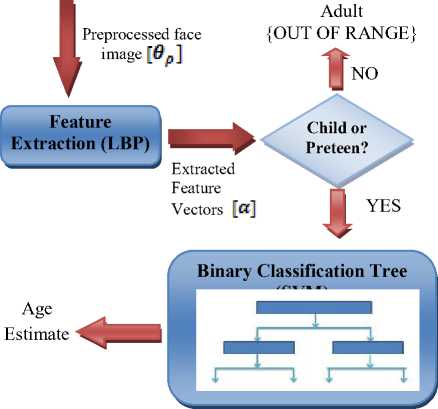
Fig.2. General overview of the proposed system

Obviously, the input into the system is the facial image, which undergoes different forms of preprocessing in order to prepare it for the feature extraction stage. The input image is first converted into grayscale, which is easier to process because it is lower in dimension than its coloured counterpart, and the region of interest (the internal part of the face or simply the facial part) is detected, cropped and resized so that only this part is presented to the feature extraction stage for further processing. Feature extraction is done with LBP and all classifications employed SVM for determining the particular age group to which each face belongs at each level of the classification tree.

• B.    Feature Extraction with Local Binary Pattern (LBP)

Feature extraction is a type of dimensionality reduction that efficiently represents interesting parts of an image as a compact feature vector. There are several features on the human face that could be extracted for different analytical purposes but for the purpose of our study, only age-related information is relevant, thus, we require only age-related facial features and this necessitates the selection of relevant features out of the extracted features for use in our algorithm. The skin around the eyes has been reported to be the most significant for automatic age estimation [32]. Hence, for the purpose of this work, we explore facial textural variations with special attention on pixel information around the eyes. The idea of using LBP for face description is motivated by the fact that faces can be seen as a composition of micro patterns that are well described by the LBP operator which also captures low level pixel information in an image.

The LBP operator was first introduced as a complementary measure for local image contrast [33]. It is a simple but very efficient texture operator which labels the pixels of an image by thresholding the neighborhood of each pixel and considers the result as a binary number. The first implementation of the operator worked with eight-neighboring pixels, using the value of the center pixel as a threshold. An LBP code for a neighborhood was produced by multiplying the threshold values with weights given to the corresponding pixels, and summing up the result.

In Image Texture Analysis (ITA), the calculated LBP codes are collected into histograms which are compared thereafter. However, this does not preserve the spatial/location information of the texture features, therefore in using LBP for facial image description; the spatial information is retained while collecting the texture information into histograms. To achieve this Ahonen et al. [34] introduced the building of local descriptions at different regions of the face which are then combined to form a global description. The ability of LBP to represent texture information on the face at three levels – pixellevel, local region level and the global level – is one of the factors that make it robust to illumination and gray level changes in an image.

Our LBP derivation follows that represented by Ojala et al. [35].

Definition 1: Let us define texture T as the joint distribution of the gray levels of P +1 (P > 0) image pixels:

T = t (gc , g 0,—, gp -1) (1)

Where g c corresponds to the gray value of the center pixel of a local neighborhood and P is the number of sampling points. g_p ( p = 0, — , p — 1) corresponds to the gray values of p equally spaced pixels on a circle of radius R(R>0) that form a circularly symmetric set of neighbors.

Without losing information, gc can be subtracted from gp as follows:

T = t (gc , g 0 - gc ,—, gp-1 - gc )

Assuming that the differences are independent of g c , the distribution can be factorized:

T * t(gc ) t(g 0 - gc ,^, gp-1 - gc )

Since t(g c ) describes the overall luminance of an image, which is unrelated to local image texture, it can be ignored:

T * t(g 0 — gc ,—, gp -1 — gc )

Although invariant against gray scale shifts, the differences are affected by scaling. To achieve invariance with respect to any monotonic transformation of the gray scale, only the signs of the differences are considered:

^T * t ⁽ s ⁽ g 0 — g c V', s ( g p - 1 — g c ))       (5)

Where s ( x ) =

1, x >  0

0, x <  0

Now, a binomial weight 2^p is assigned to each sign (g ₀ – g _c ) , transforming the differences in a neighborhood into a unique LBP code:

p - 1

LBP pr = 2 s ( g p - g c )2 p         (7)

p = 0

Where g _c corresponds to the gray value of the center pixel (x _c , y _c ) , g _p refers to gray values of P equally spaced pixels on a circle of radius R . These parameters are indicated by the notation LBP P,R . For example, the LBP operator with radius of 1 pixel and 8 sampling points is denoted LBP 8,1 .

We shall denote the collection of LBP features histogram as a ^ LBP(Op )            (8)

Where θ _p denotes the preprocessed facial image.

Subsequently, we will discuss the iterative binary classification approach with which we employed various SVM classifiers in an hierarchical tree structure to achieve multi-class SVM classification for the age classification problem.

• C.    Recursive Binary Classification with Support Vector Machine (SVM)

Support Vector Machines (SVM) is a Machine

Learning algorithm which has proven very successful in various classification problems. SVM was proposed by Vladmir Vapnik [36] with attractive features such as Structural Risk Minimization (SRM) which is superior to the Empirical Risk Minimization (SRM) principle used in Neural Networks and has thus, contributed to its success and preference to the traditional Neural Networks in the Machine learning Community.

Given two sets of training data, SVM finds a margin which separates the given points with the maximum possible distance from the closest point on both sides of the margin. This margin is called the separating hyperplane (or simply, the plane) and the points trapped by it are called support vectors because, although part of the training vectors (points), they are different in that they help in maximizing the margin. Maximizing the hyperplane is intuitive because it prevents misclassifications due to slight errors or the classification of training points with similar but different distribution patterns.

We first give a brief overview of the basics of SVMs for binary classification and explain how this technique was expanded to deal with our binary classification tree.

Definition 3: Given N training points (x ₁ ,y ₁ ), (x ₂ ,y ₂ ), …, (x N , y N ) with x i ϵ {-1, 1}, i=1,…,N and suppose these points are linearly separable; we have to find a set of N s support vectors S i (Ns ≤ Ns) , coefficient weights α i , constant b and the linear decision surface, as in (9), such that the distance to the support vectors is maximized:

w ∙ x + b = 0                  (9)

Where

Ns w=2 aysi           (10)

i = 1

Definition 4: SVMs can be expanded to become nonlinear decision surfaces by first using a mapping Φ to map these points to some other Euclidian space H that is linearly separable with a given regularization parameter C > 0, Φ:Rn →H, and by defining a kernel function K, where K(x , xj) = Φ(xi), Φ(xj). Then, the nonlinear decision surface is defined as:

Ns

2^ayK (si, x) + b = 0

i = 1

Where α and b are the optimal solution of a Quadratic programming (QP) problem as follows:

min w , b , _e   H I + C 2 ^£ i y i ^{( w} • x ⁺ b ) > ¹ - ^£ i

With ε i ≥ 0

SVMs were originally designed as binary classifiers, hence they classify a set of data into one of two classes usually written as [0, 1] or [-1, 1] . However, approaches that address a multi-class problem as a single “all-together” optimization problem exist, but are computationally much more expensive than solving several binary problems. A variety of techniques for decomposition of the multi-class problem into several binary problems using Support Vector Machines as binary classifiers have been proposed, and several which are widely used are One-against-all (OvA), One-against-one (OvO), Directed acyclic graph SVM and Binary tree of SVM (BTS). The two common methods for building a multi-class SVM classifier:

• 1.    The one-versus-all method trains one classifier for each label l _i , which separates between l _i and all other classes. A new sample is assigned to the label with the highest classifier output.

• 2.    The one-versus-one method trains one classifier for each pair of labels and the sample is assigned to the label with the most votes.

We propose a SVM Based Binary Classification Tree that uses SVMs for making the binary decisions in its nodes. The SVM Based Binary Classification Tree (SVM-BCT) method functions by recursively dividing the classes in two disjoint groups in every node of the classification tree and training a set of SVM that will decide in which of the age groups the input facial image sample should be assigned this continues until a leaf node is reached representing the age class label to which the input face belongs. At each node, combinations of several SVMs are trained using two of the classes and all samples in the node are assigned to the two sub nodes derived from the previously selected classes. This step repeats at every node until each node contains only samples from one class. Our classifier approach, SVM-Based Binary Classification Tree (SVM-BCT), takes advantage of both the efficient computation of the tree structure and the high classification accuracy of SVMs. We further improved the accuracy of our proposed classification by introducing an overlapping function which resolves conflicts or overlaps in the output of two different classifiers.

Utilizing this architecture, several SVMs are trained at a particular node and also at any entry point into any particular node using the one versus all approach. This can lead to a dramatic improvement in classification accuracy when addressing problems that have high similarity occurrences between two subclasses of a node. The recognition of each sample starts at the root of the tree and at each node of the binary tree a decision is made about the assignment of the input pattern into one of the two possible groups represented by transferring the pattern to the left or to the right sub-tree each of which may contain multiple classes. This is repeated recursively down the tree until the sample reaches a leaf node that represents a defined age group. For this reason, all training samples are mapped into the kernel space with the different kernel functions that are to be used in the training phase. In some cases there are conflicts or overlaps in the classification of the same set of data by two differently-kernelled classifiers. For this kind of situations, we developed an overlapping function that works with the classifiers at each node to help resolve classification overlaps/conflicts and increase age classification accuracy.

We give below, the mathematical model of our proposed recursive multi-class binary classification approach for age estimation:

Definition 5: Given a set of γ of age classes/labels (preteen ages), an input feature vector α _i (as obtained in (9)) and a binary classifier C _k,l ( k identifies the level of the tree, while l identifies a unique classifier at that tree level), we have the following:

Y = {Xj | Vj = 1,2,3, _,n}(13)

[π(k,l) , ρ(k,l)+1] ← C(k,l)(αi)

Where

π(k,l),ρ(k,l)+1⊂γ(15)

and

π(k,l) ∩ρ(k,l)+1=φ(16)

Equation (15) is the recursive step of the classification. At each k^th step of the recursion, 2^k classes could have been spawned, but α i will only fall into one of the two classes per step, therefore forcing the classification in the direction of α _i ’s class. At each k^th step, each π (_k,l) and ρ (_k,l)₊₁ is split into two smaller subsets, [ π (_k,l) , ρ (_k,l)₊₁ ], this is repeated until a leaf node λ j is arrived at, which is the age class of α _i . Fig 3 is a graphical representation of our proposed model.

Definition 6: For overlapping or conflicting classes, an overlapping function, σ considers the output of two different complementary classifiers in order to determine the correct classifier output at that particular classification level.

[ π ( k , µ ) , ρ ( k , µ ) + 1 ] ← σ ( C k , l , C k , l + 1 )        (17)

The overlapping function in (17) works on the output of the two complementary classifiers in a classification level to determine the correct age class to which an input image belongs. The age class produced by σ(.) is therefore dependent on the output of both classifiers and not just one of them, therefore making the resultant class π (k, μ) and ρ (k, μ)+1 .

Note that (15) could have been written as a recurrence relation which shows the efficiency (in terms of timeorder) of the classification. However, we have chosen the representation in (15) because we are not as interested here in the time-efficiency of the classification as in the classification accuracy; more so, it is typical of the representation of a classification problem in Machine Learning.

Input image feature vector ( a_f)

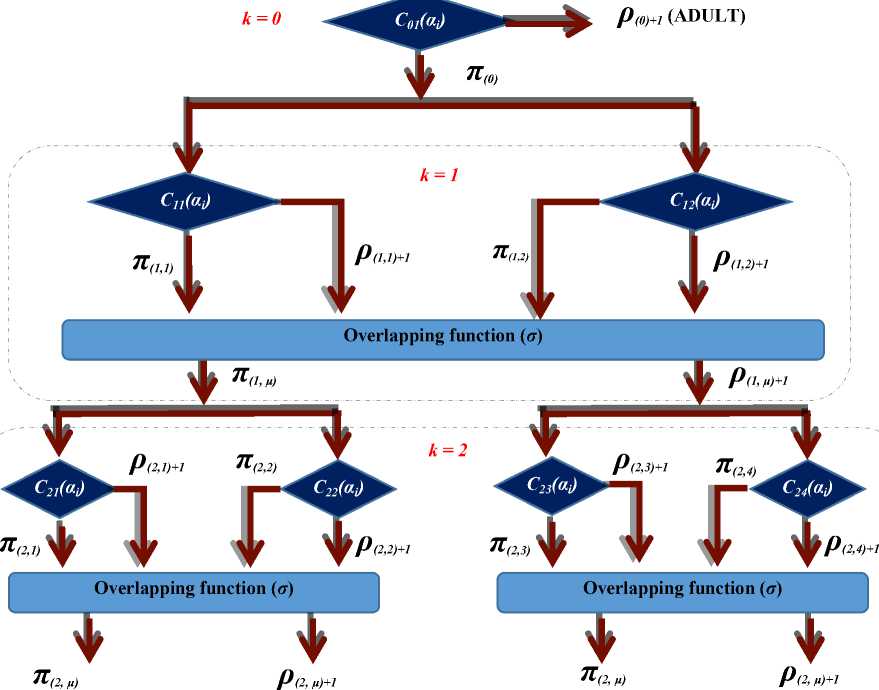
Fig.3. Recursive Binary Classification Tree

We present in algorithms 1 and 2, the proposed age estimation approach and our overlapping function respectively.

Binary Classification: Classify α into Z adult or

Z pre-teen ( γ)

Recursive Binary Classification:

Define Z, the set of Age labels: Z = {Z preteen , Z adult } and Z_pre-teen = γ, the set of pre-teen age labels as

Y = M J V i = 1,2,3,..., n}

Input face image ( 9)

Preprocess 9 to obtain 9 p

Feature Extraction

Compute LBP: α ← LBP ( θ )

If α is classified into γ then k = 1, l = 1

do

[ π ( k , l ) , ρ ( k , l ) + 1 ] ← C ( k , l ) ( α i )

If there is an overlap or conflict in classification at this level

[ π ( k , µ ) , ρ ( k , µ ) + 1^{] ← σ ( C}k , l ^{, C}k , l + 1⁾

(detailed in algorithm 2)

k = k + 1

While neither of π (_{k, μ}) nor ρ (_{k, μ})₊₁ is a leaf node (i.e. ≠ λ j for all j=1,2,3,…,n ) else

• α is an ADULT

• 7. Output the leaf node ( λ j ) reached as the age class for input image θ

Algorithm 1: Proposed age estimation algorithm

• 1.    Input pair of disjoint age groups

• 2.    For each pair of disjoint age groups

• a.    Use three different-kernelled classifiers for each age group (to classify the facial image)

• b.    For each pair of kernelled-classifiers: let P _r = kernel r; where r=1,2,3

• i.    Compare the output of classifiers of corresponding kernels across each age group:

• ii.    [a, d] ^ a(Ck,i, Ck,i+i)pr | a = agree, b = disagree

• iii.    r = r + 1

• c.    If | a| >   |d| : i.e. there  are more

classifiers  agreeing than those that disagree

• i.    Output                 classes:

[П(k,ц), P(k,ц)+1]        for which the kernelled classifiers agree

• d.    Else: i.e. there are more classifiers disagreeing than those that agree

• i.    Proceed to the next level of the tree and repeat steps b(i) to c(i)

• ii.    Backtrack to previous tree level and determine output classes based on the result from d(i) above.

Algorithm 2: Algorithm for the overlapping function

• IV. Experiments and Results

We implemented our proposed age classification approach with a Binary Classification Tree (BCT) that uses Support Vector Machine to make its binary decision at each level of the tree. As earlier discussed, our Binary Classification Tree approach uses an overlapping function to classify overlapping classes at every level in our classification tree, unlike other multi class classification that do not solve the overlapping issues within classes.

Our experiments were carried out using the publicly available FG-NET facial ageing dataset [4] which contains 1002 facial images of 82 Caucasian subjects within the ages 0 – 69 years, and our local dataset which was collected as a second album of our FAGE dataset [22]. FAGE Album 2 is a collection of facial images of indigenous Africans within the ages 3 – 11. Details of the distribution of ages and gender in the dataset is shown in table 1 and figure 4 shows sample images from the two datasets mentioned above.

ш1:

• (a) t^t ^

• (b)

• Fig.4.    Sample images from the datasets used in this work – (a) FAGE album 2 (b) FG-NET

Our experiments were focused on the age range 4 – 11 years within the FAGE album 2 and FG-NET datasets. This was intended to investigate the impact of texture features on childhood faces which are believed to exhibit more shape changes than textural changes and our results show this. Our experiments on the FAGE 2 album dataset also indicate the superiority of our proposed approach for age classification of indigenous African child faces which is not yet available in any standard facial ageing dataset. To the best of our knowledge, MORPH contains facial images with ages 16 years and above.

The basic construction of our proposed SVM-Based BCT involves two basic stages: the training Stage and the testing Stage. The feature vector extracted by LBP from the facial image is used for both stages. To use extracted features in SVM, it is important to first scale the parameters of the feature vectors to a fixed range, for example {0, 1}, to avoid that the parameters with huge ranges dominate the ones with smaller ones.

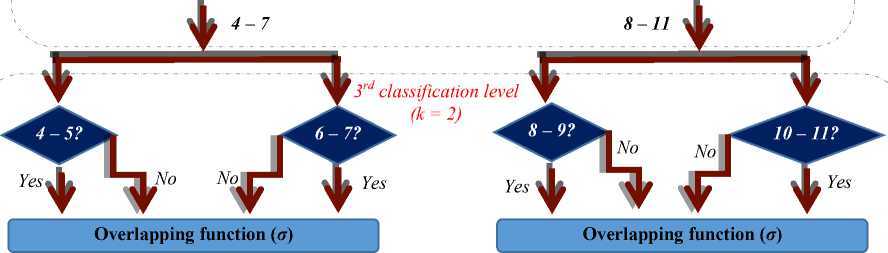
Our proposed SVM-based BCT is implemented as shown in figure 5. The pre-teen age (4 – 11) is recursively divided into disjoint age classes down the tree until a final age class is arrived at. Therefore, for an input training or test image, only one path is followed down the tree to determine its age class. Obviously, there are seven classifiers that need to be trained in implementing our proposed recursive binary classification tree. Since only one path needs be followed in classifying an input image, only P n / 2 ^ (where n is the total number of classifiers in the tree) classifiers need be used for testing. However, in some exceptional cases, where it is difficult to decide the class of an image due to confusion in the outputs of the different classifiers at that level as shown in algorithm 2, there may be need to use all classifiers at the lower level before coming back to fine-tune the result at the higher level.

Our overlapping function (σ) is implemented here as follows. Each classifier (level k=1 downwards) is implemented with three different kernels selected from multilayer perception kernel (mlp), quadratic, polynomial, least squares (ls) and Gaussian Radial Basis function kernel (rbf) and these kernels differ at each level of the tree. At level 2 (where k=1), we used rbf, polynomial and quadratic to implement both classifiers c11 and c12 (shown in figure 4); at level 3 we used quadratic, ls and mlp kernels for the first pair of classifiers c21 and c22 and the quadratic, ls and rbf kernels for the second pair of classifiers c23 and c24. Therefore, at each level, the outputs of each pair of classifiers are compared (kernel to kernel) and if more kernelled classifiers are seen to agree than disagree, we adopt the result of the agreed classifiers as the output of the classifier for that age group according to algorithm 2.

Input image feature vector ( α_i )

–

11?

No

(ADULT)

1st classification level (k = 0)

No

2nd classification level (k = 1)

Yes

Yes ▼   (4 – 11)

No

Yes

Overlapping function ( σ )

10 – 11

• Fig.5.    Implementation of the proposed SVM-based BCT

A total of seven classifiers were trained using training data from the mentioned datasets. Our training and testing tasks were implemented with the LIBSVM library [37] with MATLAB functions like svmclassify(.) to classify using Support Vector Machine and svmtrain(.) to train Support Vector Machine classifiers. We scale the parameters of the feature vectors to {0, 1} in order to avoid higher values dominating the lower ones. We evaluated the performance of our approach with cross validation, using 4-fold, 5-fold, 10-fold and random partitioning. When optimizing the parameters with the cross validation the training and testing sets were chosen randomly in each fold, so the results can slightly vary between two optimization runs. Due to this fact all experiments were run several times, to get the average performance.

Table 2. Mean Absolute Errors (MAE) on Different Training/Validation Configurations

Training / Validation Configuration	MAE OF 1st LEVEL	MAE OF 2nd LEVEL	MAE OF 3rd LEVEL	Average Mean Absolute Error (MAE)
CVPartition (80-20)	0.2963	0.7407	0.6667	0.5679
CVPartition (70-30)	0.8000	1.2000	1.0000	1.0000
CVPartition (60-40)	0.1481	1.1111	1.1852	0.8148
CVPartition (50-50)	0.2500	0.9375	0.7500	0.6458
4-fold CV	0.5000	1.3750	1.4375	1.1042
5-fold CV	0.2963	0.8889	0.6773	0.6208
10-fold CV	0.6154	0.9231	0.7692	0.7692

Table 3. Comparison of SVM-BCT with other Multi class classification approaches

APPROACH	ACCURACY (%)
One-versus-rest (OVR)	87.9
One-versus-one (OVO) method	86.55
Directed Acyclic Graph (DAG)	87.63
SVM-BCT	88.33

Table 4. Comparative Analysis of Age Estimation Accuracy on Cross Validated Data Set (FG-NET)

Algorithm	MAE
KNN	7.7062
AdaBoost	5.4386
SVM-BCT	0.7889

Table 1. Distribution of age and gender in FAGE album 2 dataset

Age (years)	Male	Female	Quantity
3	0	1	1
4	5	3	8
5	10	7	17
6	6	8	14
7	4	8	12
8	5	13	18
9	9	12	21
10	8	12	20
11	6	5	11
TOTAL	53	69	122

observed on a set of tested data as shown in equation (19). Most age classification methods have been evaluated by their Percentage Accuracy (PA) on prediction. Therefore, in order to compare the performance of our age classification method with other popular multi-class SVM methods (OvO, OvA etc.), we used the percentage classification accuracy as given in (20).

MAE =

CS ( S ) =

N

N ^

Е Ук - Ук 1

к = 1             /

к = 1

^

N

Е S Ук - Ук ^ ^ I N х100%

к = 1

In discussing our results, comparison with the widely used multi-class SVM methods like “one-against-one” (OvO) and “one-against-all” (OvA), for multiclass approaches in age estimation is presented using standard benchmarks. The standard evaluation metrics for facial age estimation are Cumulative Score (CS) and Mean Absolute Error (MAE). CS is given as the proportion of test images whose absolute error is not higher than a particular value (in years), say, Ԑ as shown in equation (18) while MAE is defined as mean/average error

PA = (N y / N) × 100%            (20)

Where

N=size of the test face images y=actual/ground truth age

=predicted age

N _y =size of correctly classified face images

As seen in table 2, the MAE at each level of the classification tree was evaluated using the mentioned validation protocols. It is observed that performance degraded down the tree (as the range of age class labels reduced). However, the best two results were obtained with the 80-20 (i.e. 80% training set and 20% test set) random partitioning and the 5-fold cross validation respectively on a combination of both datasets. As mentioned earlier, we also compared the performance of our proposed approach to other approaches for using SVM for multi-class classification. Table 3 shows that the proposed SVM-BCT performs better than the other approaches compared. The accuracy of our algorithm on FG-NET and FAGE album 2 datasets are 88.33% and 74.33% respectively indicating the impact of dataset size on classification results; FAGE has just 122 images in the age range 3 – 11 years while FG-NET has 345 images in the same age range. However, the results of our proposed algorithm on both datasets are still significantly comparable with those of existing works as shown in table 4.

• V. Conclusion and Future Directions

This work proposed a recursive SVM binary classification tree for classifying facial images into their respective ages. From our experiments, the results obtained are at par with those of existing works. This supports the intuition behind our recursive multi-class binary classification. Our proposed approach also showed good performance on indigenous African faces represented in our locally collected facial image dataset. Although, the proposed model was experimented on a small age range in (3 – 11 years), the results show that the intuition of the approach could give impressive results if tested on a wider age range. Future works will therefore focus on experimenting with the proposed approach on a wider age range.

Acknowledgment

The authors wish to appreciate Andreas Lanitis for providing us with his personal copy of the FG-NET dataset and the University of Ibadan Staff School, Ibadan Nigeria for giving us permission to obtain the facial images of their pupils for use in this work.