A Review on the Suitability of Machine Learning Approaches to Facial Age Estimation

Published Online December 2015 in MECS DOI: 10.5815/ijmecs.2015.12.03

Facial age estimation can be defined as the task of automatically assigning an exact age label (or age range) to an individual facial image [1]. Usually, humans instinctively guess or predict an individual’s age from his/her face and this human ability has been observed to be innate and possessed early in life [2, 3]. Therefore, in making the computer predict human age, the assumption is that the facial image of an individual gives sufficient ageing information about such individual. This assumption has been long established as a fact from previous age estimation algorithms which employed the facial image as the primary input. In humans, the accuracy of a predicted age depends on (among several other factors) the experience and exposure of the individual who is predicting the age, for instance an individual who works with a crime investigation agency might predict human ages better than a school teacher simply because of the differences in their trainings and frequent interactions and experiences. For a machine, however, the task is somewhat more difficult as ageing is affected by several intrinsic factors (gender, race, heredity etc.) as well as extrinsic factors (weather, drugs, condition of living etc.). Also, the temporal nature of ageing and the fact that ageing patterns are individualistic also contribute to the difficulty of age estimation as these have made it difficult to gather facial ageing dataset suitable enough for tackling the problem – this is further explained in section 2 of this paper.

Machine Learning has been defined as an automated computing procedure based on logical or binary operation which learns a task for a series of examples [4]. It often involves enabling the computer to automatically perform some tasks by training it with examples of such tasks. The challenging nature of age estimation has presented Machine Learning as a typical solution to the problem over the years. As it is with humans, the accuracy of automatic age estimation therefore depends on several factors two of which are the amount of data available for training and the performance (generalization) of the chosen learning algorithm. The various approaches employed in previous age estimation research have resulted in different age estimation accuracy levels, which have improved over the years, indicating improvement in this field of research. Due to the challenging nature of facial age estimation, efforts to improve the accuracy of age estimation is still very much on and researchers keep investigating several approaches in order to further improve results. The aim of this paper therefore is to present a comparative analysis of the performance of some Machine Learning algorithms popularly used for age estimation in order to serve as a guide for the choice of appropriate learning algorithms and feature extraction techniques for future research.

In order to ensure fairness in our evaluation of the performance of these algorithms, we employed certain standard metrics particular to age estimation and widely available in most literature. Precisely, we considered the facial ageing dataset used and the standard age estimation accuracy metrics. However, to justify the differences in the manner of application of the algorithms, we also present brief description of the methodology employed in the research in terms of facial features description or extraction techniques used. The rest of this work is organized as follows; section II discusses two popular facial ageing datasets, while section III discusses previous works in age estimation classifying them according to the Machine Learning approach used. Section IV discusses the various Machine Learning algorithms that have been used so far for age estimation and it also examines two particular algorithms which have proven very successful for age estimation. Section V concludes the writing stating the significance of this work and its expected impact on future research in age estimation.

• II.    Facial Ageing Datasets

The use of Machine Learning to automate tasks, especially one as challenging as age estimation, requires the use of sufficiently relevant training examples; this is a particularly influential factor on the accuracy of age estimation algorithms [5]. Luu et al., in [6] described the intriguing nature of the problem of age estimation stating that it is influenced by biomechanical factors which affects the natural ageing patterns observable even in identical twins. The challenging nature of age estimation was further explained in [5, 7] referring to these biomechanical factors as external factors (e.g. health, lifestyle, weather conditions, gender, race etc.) which make it difficult to arrive at a generic model for estimating human age.

Geng et al., [5] highlighted three important properties of an ideal facial ageing dataset as follows:

• I.    It should contain facial images for a large number of individuals cutting across different ethnicities, gender and age ranges.

• II.    For each subject, it should contain images for a wide range of ages

• III.    It should contain facial images of every subject for every age including future ages.

Obviously, it is difficult to obtain a dataset satisfying all these conditions. For instance, so far, it is impossible to collect images of future ages and to the best of our knowledge, none of the currently available databases have been able to meet all three conditions and this situation has posed great difficulties in facial age estimation. However, some facial ageing datasets which have shown successful results in previous works, meet some of these requirements to a reasonable extent. We discuss briefly, two popular facial ageing datasets which have recorded good performance in age estimation in previous works.

• A.    The Face and Gesture Recognition Research Network (FG-NET) Database

  The FG-NET [8] is a publicly available facial ageing dataset (gathered by Andreas Lanitis) which has been widely used in many reported age estimation research. The FG-NET is a facial ageing database consisting of 1002 images of 82 unique individuals of Caucasian descent, with ages ranging from 0 – 69 years. Individuals in the dataset have a minimum of 6 and a maximum of 18 images of different ages and the average number of images per individual is 12 images. The dataset contains coloured as well as grayscale images with variations of poses and illumination and contains exactly 34 female individuals and 48 male individuals.

• B.    The MORPH Database

  MORPH [9] is the craniofacial morphology database of the University of North Carolina Wilmington gathered for the purpose of aiding research in age progression and human recognition. MORPH is a growing database containing a relatively large number of images. As at 2013 [10], MORPH contains 55,134 unique images of more than 13,000 individuals between ages 17 – 67 years. The maximum age difference between the images of any single individual in MORPH is 1681 days (approximately 5 years). MORPH is a multi-ethnic database containing 42,589 images of Africans and generally contains facial images of 46,645 males and 8,489 females. MORPH can therefore be said to be imbalanced in its representation of gender and ethnicity.

Upon careful observation of these datasets, it is obvious that none of them completely meet the requirements stated above for a standard facial ageing dataset. However, to some extents, they both complement each other in meeting at least the first two requirements. While MORPH contains a large number of facial images cutting across different ethnicities, FG-NET is typically a mono-ethnic dataset with fewer images than MORPH but with more images per individual (cutting across different age ranges) than MORPH. Therefore, MORPH is often suitable for multi-ethnic age estimation while FG-NET particularly offers good generalization (in terms of individual ageing patterns) over a single type of ethnicity. Our evaluations in this paper will be principally based on these two datasets in order to allow for a fair judgment of the performance of Machine Learning approaches used in age estimation and to keep this paper focused. For a more comprehensive review on age estimation, interested readers can consult [1].

• III.    Age Estimation and Machine Learning

Previous works in age estimation have employed several Machine Learning approaches for solving the age estimation problem. The choice of Machine Learning algorithm used is often influenced by (among other factors) the approach of the research to the age estimation problem. Onifade and Akinyemi in [11] observed that these approach can be classified into five categories as shown in figure 1 (adopted from [12]); namely the Anthropometric Model (which employ the measurement of change in facial shape) Ageing Pattern Subspace

(which employ the synthesis of ageing faces), the Multiclass approach (which considers the problem a classification problem), the Regression approach (which considers the problem as a regression problem) and the Ranking approach (which estimates ages by comparing facial images across different individuals and ages in order to determine age ranks inferences of which are in turn used for age estimation).

Upon careful examination, it can be deduced that the classification employed in most age estimation works is based upon the age determination approach as well as the age-image representation. However, the focus of this work is on age determination and in this regard, age estimation approaches fall into three categories; the first two being the two classes of Machine Learning algorithms as discussed in sub-sections 3.1 and 3.2; classification and regression, and the third category (discussed in sub-section 3.3) is a hybrid of the first two categories. Typically, age estimation can be viewed as a special Pattern Recognition problem [1] in that it can be viewed as a classification problem, a regression problem or a combination of both. In the case of classification, age estimation is a multi-class classification problem in which age labels (or age range labels) are considered as classes into which facial images are classified while in regression, the age labels are considered as a set of ordinals (i.e. sequentially ordered integers) to which the regression function fits facial images.

In this paper, we reviewed a number of works in which age estimation was approached as a classification problem and those in which it was approached as a regression problem as well as those combining both methods in certain ways and we compared the performances of these methods on popular facial ageing databases in order to evaluate their performances. We believe such information as presented in this paper is useful to the age estimation research community in guiding researchers’ choice of Machine Learning approach for age estimation based on their reported performances.

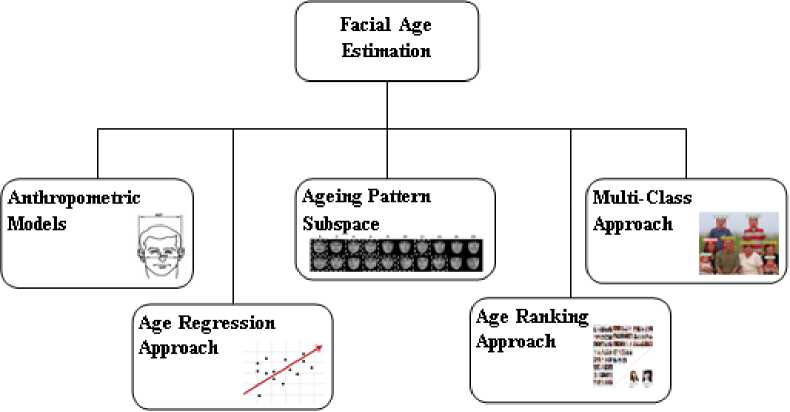
Fig.1. Classification of Age Estimation Approaches [12].

Our discussion of previous works will therefore emphasize their Machine Learning approach or the specific classification or regression algorithm employed for age determination.

• A.    Age Classification

Age classification involves assigning distinct age labels to individual facial images. This is often accomplished by training a classification algorithm on the image dataset with the set of age labels given as the classes into which facial images are to be classified. Subsequently, the classification algorithm determines the age of a test image (an out-of-training example) by assigning it to one of the age labels provided during training. Classification algorithms predict exactly one of the classes in the supplied set of classes unlike regression which predicts real (continuous) values within the supplied responses (although usually based on the fitting model).

The work of Kwon and Lobo [13] was one of the earliest in age estimation. They employed knowledge from craniofacial research and wrinkle analysis to classify facial images as babies, adults and seniors. They did not use any known machine learning algorithm, however, classification was done in two phases – primary and secondary phases. At the primary phase, they employed geometric measurements to detect and localize primary facial features (eyes, nose, mouth, chin, the virtual top of the head and the sides of the face) and 6 geometric ratios were computed as the various displacements between these features. While the primary phase distinguished baby faces from non-baby phases, they employed wrinkle analysis to further distinguish between the faces of adults and seniors. Their experiment was carried out on a small database of 47 high resolution facial images with a 100% classification accuracy on 15 test images equally distributed within the considered age classes.

Horng et al., [14] extended the work in [13] to classify facial images into babies, young adults, middle-aged adults and old adults. They employed Sobel edge operator [15] and region labelling to locate primary facial feature (eyes, nose and mouth) and obtained two geometric features and three wrinkle features. Their classification approach employed two back-propagation neural networks [16]; one used the geometric features to classify baby faces while the other network employed the wrinkle features to classify the three adult age groups. Using a dataset of 230 facial images, they trained their algorithm on half of the dataset and tested on the other half achieving an accuracy level of 81.58%.

In [17], Lanitis et al., evaluated the performance of various classifiers on statistically modelled facial appearances using Active Appearance Model (AAM) [18]. They evaluated the performance of Artificial Neural Networks (ANN), shortest distance classifier and quadratic function-based classifier. Variations of their classification method were also described using agespecific and appearance-specific age estimation methods. Presenting the same representation of each facial image to the different classifiers tested, they compared the performances of the different classifiers. For Quadratic function, optimization methods were used to determine the coefficients that best represents the relationship between facial parameters and the age of the face. Thereafter, the established function is used to fit facial parameters to the age of a facial image. From the training data, Shortest Distance Classifiers were used to map various distributions of facial parameters to ages; given facial parameters of a test image, it is then assigned to the closest distribution in order to determine the age. Supervised neural networks were trained to predict the ages of facial images, given test facial parameters. Kohonen Self-Organizing Maps (SOM) [19] was used to train supervised neural networks to map facial parameters to clusters of images corresponding to age groups. They observed that the best results were obtained using a combination of an appearance-specific and age-specific quadratic function-based classifier with an absolute error of 3.82 years using a dataset of 400 images of 40 individuals from ages 0 – 35 years.

Geng et al., in [19, 20] defined an aging pattern subspace method for estimating human age. An aging pattern was defined as a sequence of personal aging faces, therefore. To determine the age of a facial image, a representative subspace is learnt in order to determine its aging pattern – the ageing pattern which reconstructs the image with the least reconstruction error – and the position to which the image belongs in the aging pattern determines its age. This approach employs classification to determine the ages of individuals, since the positions in the ageing patterns are fixed and have associated age labels, which is considered as the age of any image which falls into that position in its aging pattern. Facial images were modelled with AAM and the algorithm demonstrated better performance that human observers on the FG-NET. In [20], Mean Absolute Error (MAE) of 6.77 was reported on FG-NET using the LOPO validation protocol and MAE of 8.83 was reported in [21] on MORPH dataset.

Luo et al., in [22] proposed a multi-label learning approach to age estimation in which they employed Multi-Label Learning (MLL)-SVM. Based on the observation that a person might have a consistent facial look over a range of years; the approach of labeling each face with an exact age however limits this assumption. The authors, therefore, proposed a MLL approach in which each facial image is labeled with its exact age as well as neighbouring ages; thus, every image has, attached to it, a series of age labels which are believed to be close enough to its actual age. Subsequently, MLL-SVM algorithm was used to predict a set of age labels for a facial image and obtain a final estimate of the actual age of the image as the arithmetic mean of the labels. Their algorithm achieved its lowest MAE of 5.04 years on FG-NET when they used a range of 6 years on each age label.

In [23], the authors, based on the fact that human faces show variations even within the same age across different individuals, proposed an age estimation approach which learns the rank relationship across individuals of the same age as well as different ages. Arguing that there is so much inference to be obtained from a pairwise comparison between images of different individuals of the same age, they built their reference set to contain both consistent and ordinal pairs. The consistent pairs were images of individuals of the same age and the ordinal pairs were images of individuals of different ages. They employed Ranking SVM [24] to obtain the ranking function during training. For a test image, the obtained ranking function is used to determine its age rank and a pairwise comparison of the obtained age rank is made with their image reference set in order to determine the age estimate. If the test image’s rank was higher than a certain percentage of images in a given age set, such an image is considered older than that age. Their approach was tested on MORPH and MultiPIE [25] datasets with MAE of 5.12 years on MORPH.

• B.    Age Regression

Regression means approximating a real-valued target function [26]. As indicated from the definition above, regression approaches in age estimation often involve training a regression algorithm with the dataset of images and their corresponding age labels which are then used by the regression algorithm’s fitting function to estimate the ages of test images as continuous values.

From their observation of a sequential pattern of lowdimensional distribution, Fu et al., in [27] proposed a model of age estimation which employed the manifold analysis of facial images to find a sufficient embedding space and model the low-level manifold data with multiple linear regression functions. In their experiments they used two linear feature extraction techniques and two manifold (non-linear) learning techniques; Principal Component Analysis (PCA), Neighbourhood Preserving Projections (NPP), Locality Preserving Projections (LPP) and Orthogonal LPP (OLPP) respectively. They employed a quadratic regression function to fit the low- dimensional image representations to ages and reported their lowest MAE as 8 years using OLPP on the UIUC-IFP database. This same age estimation framework was also employed in [28] with an introduction of another feature extraction technique – Conformal Embedded Analysis (CEA) – yielding MAE of about 6 years on the same dataset.

In [7], the authors employed manifold analysis of face pictures to reveal underlying facial features and used a locally adjusted regression approach to estimate the age of subjects. In their approach, non-linear Support Vector Regression (SVR) was used to fit a regression function for age estimation. Based on the observation that age estimates obtained via regression could be far from the true ages, their idea of locally adjusted regression specifies an age range within which the age estimate is adjusted up or down in order to obtain an estimate closer to the true age. Using the age ranges of 4 and 8 years, they obtained the lowest MAE of 5.07 on FG-NET with LOPO validation protocol.

Yan et al., in [29] proposed a patch-based regression framework for estimating human age and head-pose. In their three-staged model, they first encoded images using Gaussian Mixture Model (GMM); thereafter, they used a patch-kernel to characterize the Kullback-Leibler divergence between the models of any two images and this was enhanced by a weak learning process which they regarded as inter-modality similarity synchronization, finally, they used kernel regression [30] to estimate human age. MAE of 4.95 years, 4.94, 4.38 were obtained on the FG-NET dataset, Yamaha female dataset and Yamaha male dataset respectively.

Ricanek et al., [31] proposed a generalized multi-ethnic model for facial age estimation. They modelled facial images with AAM and employed Least Angle Regression (LAR) to select features relevant to age estimation and then used SVR to fit an age estimation function. They tested their algorithm on FG-NET, MORPH and PAL datatsets and obtained MAE of 5.7 on FG-NET and between 5 and 6 years on each of the ethnicities in the MORPH database.

Guo and Mu [32] proposed a robust dimensionality reduction and facial age estimation using Kernel Partial Least Squares Regression (KPLSR). Being an extension of their earlier work in [33] in which they employed Partial Least Squares Regression (PLSR) to determine gender, ethnicity and age, they reported that KPLSR was able to select features in a lower dimensionality, selecting about 30 latent variables which were eventually used for age estimation. They reported MAE of 4.18 years on MORPH dataset.

Yan et al., [34] applied ordinal/ranks to training image samples with uncertain labels using bilinear fusion of candidate kernels from which inferences were made for determining the ages of facial images. They regarded the relationship between facial images and their ordinal ranks using the concept of uncertainty. In their approach, low level image features were learnt by bilinear transformation and projected into the desired rank of the images. Maximum a Posteriori (MAP) was then used to derive the parameters for the ranking model and these parameters were estimated using ExpectationMaximization (EM) in which they used a linear regression model to map the kernel function to ordinal ranks of facial images. The tested their approach on FG-Net and Yamaha datasets and reported MAE 5.33 on FG-NET using LOPO validation protocol.

Chao et al., [35] proposed an age-oriented local regression approach to age estimation with the following three contributions; explored the relationship between facial features and age labels using distance metric learning and dimensionality reduction, solved the problem of imbalanced age classes available in most facial ageing datasets and exploited the intrinsic ordinal relationship among ages using a label-sensitive concept. Using AAM for face representation, they proposed a label-sensitive Relevant Component Analysis (lsRCA) and label-sensitive Locality Preserving Projections (lsLPP) for distance metric adjustment. They experimented with their proposed approach using several combinations of learning algorithms and found the combination of K-Nearest Neighbour (KNN) and SVR to produce the best results with MAE of 4.38. They carried out their experiments on FG-NET using the LOPO validation protocol.

In [3] and [36] proposed a groupwise age-ranking framework for facial age estimation. Using Local Binary Pattern (LBP) to extract texture features from the face, they first determined the age groups into which facial images belonged and then employed Least Square Boosting (LSBoost) [37] in an ensemble learning framework for age estimation. They tested their approach on FG-NET and a locally collected facial ageing dataset, FAGE and reported MAE of 2.34 years on FG-NET images in the age range of 13 – 40 years using LOPO.

• C.    Age Classification and Regression

Although, the technical categorization of machine learning algorithms is either as classification or regression, we cannot ignore the fact that some works employed a combination of both in training and testing for facial age estimation – such works are often said to employ a hybrid approach to age estimation. This is often due to the challenging nature of age estimation which has necessitated the investigation of both machine learning approaches in order to obtain more accurate estimates. However, this does not make the machine learning methods hybridized; rather, these approaches are technically a combination of both methods (classification and regression) in some way. In this section, we discuss such works and indicate how the combination is realized in order to allow a proper evaluation of the performance of the learning frameworks employed.

Guo et al., in [38], proposed a probabilistic fusion approach in which they employed the fusion of a regressor and a classifier to predict ages. Facial image was represented with AAM and their algorithm was tested on FG-NET using the LOPO validation protocol and UIUC-IFP-Y databases. The classifier used was Support Vector Machine (SVM) [39] and Support Vector

Regression (SVR) [39] was used as the regressor. The fused age estimator was derived by combining the outcomes of the regressor and the classifier to probabilities and then fusing them automatically. Although this approach is a hybrid of the classification and regression methods, while the regressor was implemented to improve the decision of the classifier, the classifier gives the final age estimate. They found SVM to be better on FG-NET than SVR while SVR was better on the UIUC-IFP-Y database than SVM. In the long run, their fused age estimator had better performance than both SVM and SVR used independently, obtaining MAE of 4.97 years on FG-NET, while SVM had MAE of 7.16 – similar to what was obtained with SVM in [40].

In [2], the authors used Biologically-Inspired Features (BIF) to represent facial images and employed both classification and regression for age estimation using SVM and SVR. They employed SVM on the Yamaha Gender and Age (YGA) database using 4-fold cross validation and SVR on FG-NET using LOPO validation protocol. They reported MAE of 4.77 years on FG-NET and 3.91 years and 3.47 years on the female and male portion of the YGA database respectively.

In [6], facial images were represented with Active Appearance Model (AAM) and the discriminative features of AAM were used to create an Adult-Youth classifier which separated the facial images of adults (21 – 69 years) from those of young ones (0 – 20 years). Subsequently, SVR was used to further determine the exact ages of adult subjects and SVM for child subjects. Their experiment on FG-NET gave MAE of 4.37 years.

Table 1. Performance of Different Machine Learning Algorithms for Facial Age Estimation

Machine Learning Algorithm	Brief Description	Age estimation literature(s) in which it was used	Comments
ANN [43, 44]	ANN is an algorithm that provides practical methods for learning discrete-valued, real-valued and vector-valued functions from examples [26]. Although it can be used for both classification and regression, most age estimation works have used it for classification. ANN algorithms considered here include BP and MLP	[13, 16, 33, 34, 45–49]	These works were experimented on a variety of datasets ranging from the earliest ones containing 230 images to FG-NET, MORPH and Yamaha datasets.
Boosting [36, 50]	Boosting is committee-based learning framework originally defined for classification but which has been increasingly employed for regression. Boosting uses a combination of many weak classifiers to produce a powerful committee through a series voting procedure.	[33, 35, 47]	Although, these works were tested on several datasets, most of them were tested on the FG-NET dataset. However, different types of boosting algorithms were employed, basically AdaBoost and LSBoost. LSBoost as used in [36] achieved MAE as low as 2.34 years on FG-NET facial images between ages 13 – 40 years.
K-NN [44, 51]	K-NN is an instance-based learning method which assumes that all instances correspond to points in an n-dimensional plane and finds their nearest neighbours using a standard distance metric [26]. K-NN can be used for either classification or regression.	[34, 45, 46, 52, 53]	These works were all tested on the FG-NET dataset using different intuitive variations to K-NN. [53] employed sequence K-NN and ranking K-NN for predicting age group and age value respectively obtaining MAE of 4.97 years on FG-NET, while [35] used a combination of K-NN and SVR and obtained MAE of 4.38 years on FG-NET.
SVM [39]	SVM is a machine learning algorithm which finds the separating hyper-plane, between a set of points (from two sets of training data), that maximizes the distance between the closest points on both sides of the plane. SVM is basically a binary classification algorithm, but it has been adapted for multi-class classification in most age estimation works.	[2, 7, 37, 39, 40, 45, 46, 54]	Many of these works were tested on FG-NET, YGA and MORPH with MAE as low as 3.17 years on FG-NET and 4.11 years on MORPH both in [41].
SVR [39]	SVM is a machine learning algorithm which finds the separating hyper-plane, between a set of points (from two sets of training data), that maximizes the distance between the closest points on both sides of the plane. SVR is realized when a loss function is introduced into SVM.	[2, 6, 7, 30, 37, 39, 40, 45–47, 54–57]	These works were tested on a myriad of ageing datasets including FG-NET and MORPH with the best results obtained in [40, 42] with MAE of 3.17 on FG-NET and 3.31 on a combination of FG-NET and MORPH.

• IV.    Discussion

Over the years, research in facial age estimation has improved steadily in terms of accuracy. From the works discussed above, it is clear that no succinct conclusion can be made on the best class of Machine Learning algorithms (classification or regression) for age estimation. However, there are three major observations from previous research in facial age estimation which help make justifiable conclusions. First, classification and regression algorithms perform differently on different datasets, this is most likely due to the peculiarities of each dataset (age, ethnicities, and gender distribution.) Secondly, we observed that SVM and SVR are the most popular classification and regression algorithms used for age estimation and have relatively shown the best performance so far on FG-NET and MORPH datasets. Thirdly, we observed that the method employed for face modelling or facial features extraction had significant impact on the results of age estimation. Note that SVM is the Machine Learning algorithm, its usage for classification or regression gives rise to naming it either as SVC (as used in the abstract) or SVR respectively. However, because SVM was primarily designed for classification, SVC is usually referred to as SVM and the same nomenclature is adopted here.

In order to keep our discussion focused, we summarized in tables 1 and 2, these three observations with much emphasis on FG-NET and MORPH datasets. Table 1 shows the performances of five (5) different Machine Learning algorithms for age estimation on various datasets. Due to the differing characteristics of the different datasets, we consider that a strict distinction between the best and worst results of the algorithms would be biased, therefore we simply make our remarks/comments in the last column of the table stating specific highlights about some of the works which we consider notable. Table 2, however, shows the performance of SVM and SVR for age estimation on the MORPH and FG-NET datasets with clear distinction of which result is best so far on each dataset.

The standard evaluation metrics for facial age estimation are Cumulative Score (CS) and Mean Absolute Error (MAE). CS is given as the proportion (percentage) of test images whose absolute error is not higher than a particular value (in years), say, Ԑ as shown in equation (1) while MAE is defined as mean/average error observed on a set of tested data as shown in equation (2).

N

^

MAE = У У к - У к

к = 1

N

Where n is the size of the test set and y and y are the actual and predicted ages of facial images in the test set respectively.

N

CS(s ) =

У S I У к - У к к = 1    V

^

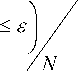
x 100

Where S(.) is a function which gets the frequency prediction errors higher than a certain age ε while other variables remain as previously defined.

From Table 1, it can be observed that SVM and SVR (either in their pure or varied forms) have generally found more usage than any other algorithm. It is also noteworthy to state that the performance of learning algorithms is dependent on many factors, among which are the size and distribution of the dataset as well as the features used. The algorithms presented in Table 1 are those which have been repeatedly tested and compared in most age estimation works, thus presenting the relative performance of these algorithms across the different factors mentioned above. Based on the popularity of SVM and SVR for age estimation and their relatively good performance, we presented in Table 2, a number of age estimation works which employed these algorithms (SVM and SVR) for age estimation indicating their performances on FG-NET and/or MORPH datasets only. To investigate the relative performances of the algorithms, we also showed the mean and standard deviation values of the MAE and CS of the different algorithms.

From Table 2, several interesting patterns are observable. First, FG-NET has been far more used for age estimation experiments than the MORPH dataset. This is probably due to some of FG-NET’s desirable characteristics as stated in section 2 (Facial Ageing Datasets) of this writing, particularly the availability of a relatively larger number of age-separated facial images per individual than MORPH because this helps algorithms to better learn the various individual ageing patterns. Also, FG-NET covers a wider age range (0 – 69 years) than MORPH does (17 – 67 years), this feature helps researchers correctly classify facial images into a wider range of ages, thus improving the usefulness of their algorithm for determining human age across a wider age group.

Secondly, it can be observed that the performances of SVM and SVR have generally improved on FG-NET more than on MORPH, this is a very likely result of the first observation stated above. To further establish this fact, it can be observed from Table 2 that the mean value of MAE on FG-NET (5.05 years) is lower than that of MORPH (6.07 years) and the mean CS value on FG-NET (85.85%) is higher than that of MORPH (49.21%), the standard deviation values as well corroborate this fact; showing lower standard deviation values for FG-NET than MORPH.

Thirdly, it can be observed that taking both Machine Learning algorithms individually, SVR has shown much better performance on both datasets than SVM. This could be traced to the nature of the age estimation problem – classification or regression. While some earlier works argued that age classification is only efficient under a sufficient representation of facial images and ages in a dataset [2], others have clearly demonstrated the better performance of SVR than SVM on the same dataset [45, 46]; more recent works [34, 55–57] have even been able to improve age estimation by employing SVR alone. However, from the results in rows 5 and 9 of Table 2, we can conclude that an intuitive combination of both algorithms perform much better than each one does on its own.

On the impact of facial features extraction technique used we observed that AAM has been the most popularly used face description technique because of its ability to model shape and texture features in a single face model. More so, AAM extracts a number of features that preserve 95% of the variability and has proven from previous works to be efficient for describing age-relevant facial features. However, as seen in row number 5 of Table 2, BIF has given the lowest MAE of 3.17 years on

FG-NET and 4.11 years MORPH so far while a combination of Gabor filters and LBP has given the best CS of 93% at error level of 10 years on FG-NET so far (row number 9 of Table 2). This goes to state that intuitive ways of using or combining existing feature extraction techniques on facial images could significantly improve research results in age estimation.

Table 2. Performance of SVM and SVR for Age Estimation

S/N	Literature	Brief Description (indicating face modelling technique in bold)	Algorithm	Dataset	Result
					MAE (years)	CS (at 10 years) (%)
1	Guo et al., 2008 [7]	A robust regression age estimation approach that employs manifold learning to represent face ageing data and uses a local adjustment of age regression results to obtain more accurate age estimates.	SVM & SVR	FG	5.07	≈ 88
2	Guo et al., 2008 [38]	Employs a probabilistic fusion of classification and regression outputs to estimate human ages more accurately. AAM parameters were used to describe facial features.	SVM & SVR	FG	4.97	≈ 88
3	Guo & Huang 2009 [2]	This work improved upon the representation of features for age estimation by using BIF which are built from Gabor filters.	SVM & SVR	FG	4.77	≈ 90
4	Luu et al., 2009 [6]	This work employed SVR for robust regression on AAM of the face from which age-relevant features are selected using LAR.	SVR	FG	4.37	≈ 89
5	ElDib  &  El-Saban 2010 [41]	This work used enhanced BIF and employed a classification and regression model for age estimation.	SVM and SVR	FG & MP	FG: 3.17 ; MP: 4.11	FG: 90; MP: NR
6	Chang et al., 2010 [46]	This work proposed a ranking framework based on a set of binary queries which results in a binaryclassification-based comparison; the results of the binary queries were then fused to determine the age of the target image. Facial features were extracted with AAM .	SVM and SVR	FG & MP	FG: (SVM: 6.72, SVR: 6.05); MP: (SVM: 7.55, SVR: 6.99)	FG: (SVM ≈ 75, SVR≈82);  MP: (SVM  ≈  70, SVR≈72)
7	Yang et al., 2010 [48]	This work used a ranking approach to select age-relevant haar-lik e features and employed a number of regression algorithms (including SVR) for age estimation.	SVR	FG	5.67	NR
8	Chang et al., 2011 [47]	This work proposed a cost-sensitive OHR which separates all images into two groups based on the relative order of their age labels and uses the cost of classification to find the best separating hyperplane and an age estimate is obtained from the aggregated cost-sensitive OHR. Facial features were extracted with AAM .	SVM and SVR	FG & MP	FG:   (SVM: 7.25,    SVR: 5.91);     MP: (SVM:   7.55, SVR: 6.99)	FG: (SVM: NR, SVR≈83);  MP: (SVM≈70, SVR≈72)
9	Choi et al., 2011 [55]	An hierarchical classifier based on	SVM and SVR	FG	4.66	≈ 93

		SVM and SVR was proposed to explore hybrid facial features (local and global features) for age estimation. Region-specific Gabor filters were used to extract facial wrinkle features and LBP was used to extract skin texture features.
10	ElDib & Onsi 2011 [43]	This work employs BIF to evaluate the suitability of different facial parts for age estimation and the areas around the eyes were shown to contain the most age-relevant features.	SVM and SVR	FG & MP	FG:      3.17; FG+MP: 3.31	FG≈70; FG+MP ≈ 80
11	Luu et al., 2011 [58]	This work investigated the use of CAM instead of AAM for face representation in order to improve age estimation.	SVR	FG	4.12	≈ 90
12	Gao 2012 [57]	In order to capture the differences in individual ageing patterns, this work proposed a multi-task learning approach by training a function to learn each individual’s ageing pattern, used a similarity function to aggregate the individual functions and employed multi-task SVR for age estimation. AAM was used for facial features extraction.	SVR	FG & MP	FG: 4.37; MP: 5.62	FG ≈ 90; MP≈90
13	Chao et al., 2013 [35]	Using AAM to model facial appearance, this work improves age estimation by exploring the relationship between facial features and age labels using distance metric learning and dimensionality reduction. Using a label-sensitive concept to solve the problem of imbalanced age classes in facial ageing datasets and finally proposed an age-oriented local regression to capture the complex nature of human ageing.	SVR	FG	5.32	≈ 89
14	Liu et al., 2014 [56]	This work proposed a hybrid constraint SVR for age estimation. First, fuzzy age labels were defined and together with the original age labels were used to train SVR for age estimation. This work employed three different feature descriptors for face modelling – SIFT , Gabor filters and GMM	SVR	FG	5.28	≈ 85
	aMean:				FG: 5.05 MP: 6.07	FG: 85.85 MP: 49.21
	aStandard deviation:				FG: 1.09 MP: 1.33	FG: 6.22 MP: 30.83

FG : FG-NET;       MP : MORPH;       NR : Not Reported;

^aMean and Standard deviation values have been calculated by spreading out multiple MAE and CS values within a cell. No value was ignored.

• V.    Conclusion and Future Directions

This work explains the impact of Machine Learning on facial age estimation with emphasis on those algorithms that have been most popularly used and those that seem to have been the most successful. Our evaluations in this review were based on the two most popularly used publicly available facial ageing dataset – FG-NET and MORPH datasets.

From this review, we were able to draw three conclusions; first, that SVM and SVR have been the most popularly used Machine Learning algorithms for facial age estimation on the mentioned datasets. Secondly, that a combination of SVM (for classification) with SVR (for regression) have shown better performance than using each one differently. Thirdly, we found that the facial feature extraction technique employed for age estimation significantly impacts estimation accuracy. In the light of this, we found that although AAM has been popularly used because of its desirable qualities in modelling facial appearance, BIF and a combination of Gabor wavelet and LBP have shown better performance than AAM on both FG-NET and MORPH. Therefore, we can summarily conclude that the results of age estimation algorithms are largely influenced, not only by the choice of the classification or regression approach, but also by the method used to model or extract features from the face – face modelling, feature extraction and feature selection.

For about a decade now, FG-NET and MORPH have been continuously used for age estimation research and the results on these datasets seem to have peaked [59]. Therefore, future directions in age estimation should investigate the problem on entirely different datasets with a wider variation in ages, ethnicity and gender than FG-NET and MORPH. Also, age estimation on real-life faces (images of low quality, usually containing occlusion and motion) is beginning to gain attention, especially with the popularity of mobile devices which can be used to obtain images from uncontrolled scenes in real-time. Although, there has been a number of works in this area now [59]– [62], the results are still not good enough because of the challenges posed by the quality of real-life images.

With regard to face modelling (facial feature extraction and selection), future research should investigate into existing feature extraction techniques that can properly describe facial shape and texture. Some of these techniques might or might not have been employed for age estimation, but a proper investigation into those techniques could be very much worth the improvement to be obtained in facial age estimation having observed the significant impact of facial feature extraction on age estimation.

This work hopes to serve as a guide for future researchers’ choice of algorithms and methods for facial age estimation in order to better improve upon existing state-of-the-art methods in the field, making the results of forth-coming research laudable and suitable for use in practical applications.