A Robust Fault Detection Scheme for the Advanced Encryption Standard

Published Online May 2013 in MECS

• I.    Introduction

  In October 2000, The Advanced Encryption Standard was finalized by the National Institute of Standards and Technology (NIST), when the Rijndael algorithm was adopted [1]. The AES algorithm replaced the data encryption standard (DES), which had been in use since 1976. Until now, many architectures, for efficient VLSI realization of AES algorithm, have been proposed and their performance have been evaluated by using ASIC libraries and FPGA [2-5]. Cryptographic algorithm AES is currently used in a very large variety of scenarios. The most common examples: e-commerce and financial transactions, which have strong security requirements [6]. Therefore, it is necessity to protect the AES implementation against the fault attacks, such as the Differential Fault Analysis (DFA) [7-12] and the Simple Fault Analysis (SFA) [13].

The fault attacks are based on injecting faults into the structure of the AES to obtain the secret cryptographic keys. The cryptanalyst injects faults during the execution of the processing algorithm. This disturbs the normal execution behavior and results in creating faulty ciphertext. Therefore, the cryptanalyst can guess secret key after certain number of the fault injections and analyzing faulty ciphertexts.

To make a robust implementation against fault attacks, several countermeasures have been proposed [14-21].

In [14], Karri et al proposed an error detection method, called concurrent error detection (CED). This fault detection model exploits the inverse relationship between encryption and decryption to detect the fault at the operation level, the round level and the algorithm level.

Yen et al proposed in [15] a fault detection based on the cyclic redundancy check (CRC). This approach uses an (n+1, n) CRC to detect the faults, where n (4, 8, 16) and the parity of the output of each transformation is predicted. The CRC fault detection can also be implemented in the operation level, round level and algorithm level.

In [16], Natal et al proposed an error detection method based on hardware redundancy. They used four S-Box for the implementation of the SubBytes transformation. They used one additional S-Box to check the result of every four S-Box.

Rajendran et al proposed in [17] a new CED mechanism based on the slide attack. This mechanism is independent of the implementation scheme of the S-Box. It can be applicable to all the symmetric block ciphers. It is applicable to both the encryption and decryption mechanisms.

In [18], Chu et al proposed new error detection method using the polynomial residue number systems (PRNS) to protect the AES implementation.

In this paper, in order to improve the security of the AES, we propose a fault detection scheme against the Differential Fault Analysis. This method combines several countermeasures presented in the literature.

The organization of this paper is as follows. The basic structure of AES is given in section II. In section III, several architectural solutions for fault detection in cryptographic systems are presented and categorized according to the type of the redundancy scheme. In section IV, we present the proposed a fault detection scheme for the AES. In section V, The fault coverage of the proposed fault detection scheme is obtained. In section VI, the implementation results and the performances report of the proposed fault detection scheme are discussed and compared in terms of area, frequency and fault coverage. Section VII concludes the paper.

Key

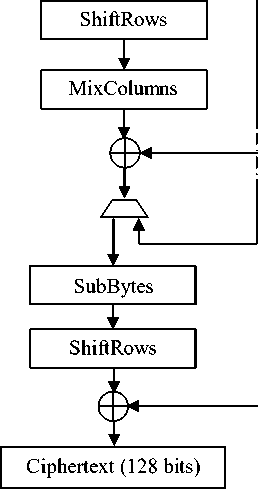
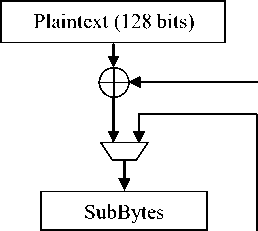
Figure 1. AES algorithm: Encryption structure

Key Expansion

• II.    AES Algorithm

• •    Apply the following affine transformation (over GF(2)).

AES is a symmetric-key block cipher with a data block length of 128 bits, which supports different key lengths of 128, 192 or 256 bits. The AES is a round-based encryption algorithm. The number of rounds, Nr, is 10, 12, or 14, when the key length is 128, 192 or 256 bits, respectively.

In the encryption of the AES algorithm, each round, except the final round, performs four transformations: SubBytes, ShiftRows, MixColumns and AddRoundKey, while the final round does not have the MixColumns transformation. The key used in each round, called the round key, which is generated from the initial key by a separate key scheduling module.

The SubBytes transformation is a non-linear byte substitution that operates independently on each byte of the state using a substitution table (S-Box). This S-Box, which is invertible, is constructed by composing two transformations:

• •    Take the multiplicative inverse in the finite field GF(2⁸), the element {00} is mapped to itself.

b i = b i Ф b . .      Ф b ( i _{+ 5})_mo_d8 Ф b ( i + 6)mod8 Ф b ( i      . Ф C (1)

for 0 ≤ i < 8, where b i is the i^th bit of the byte, and c i is the i^th bit of a byte c with the value {63h}.

The ShiftRows transformation is a circular shifting operation on the rows of the state with different numbers of bytes. As shown in (2), the first row of the state is kept as it is, while the second, third and fourth rows cyclically shifted by one byte, two bytes and three bytes to the left, respectively.

" 5 0	s 4	s 8	5 12 "		" 5 0	s 4	s 8	5 12 "
5 1	s 5	s 9	s 13	ShiftRows	5 5	s 9	s 13	s 1
5 2	s 6	s 10	s 14	'	5 10	s 14	s 2	s 6	(2)
_ 5 3	s 7	s 11	5 15 _		_ 5 15	s 3	s 7	5 11 _

The MixColumns transformation operates on the state column by column, treating each column as a four term polynomial. The columns are considered as polynomials over GF(28) and multiplied x4 +  1 with a fixed polynomial a(x) given by:

a(x) = {03}x3 + {01}x2 + {01}x + {02}           (3)

In matrix form, the MixColumns transformation can be expressed as:

s'0,j s'1,j s'2,j s'3,j

03  01  01"	■ s 0;
02  03  01	s 1, j
01 02 03	s 2, j
01  01  02	_ s 3, j _

0 ≤ j ≤ 3,

The AddRoundKey is a XOR operation that adds a round key (K) to the state in each iteration, where the round keys are generated during the key expansion phase.

• C. Information Redundancy

According to [22], the Information redundancy can be classified into three categories: parity-1, parity-16 and nonlinear robust codes.

The parity-1 uses only single bit parity for the entire 128-bit output and the fault is detected by comparing the predicted parity with the calculated parity at the end of each round.

In Parity-16, one parity bit is generated for each byte of the input and the fault is detected in the same way in Parity-1. While gaining higher fault coverage, the area overhead of Parity-16 is more than Parity-1.

The nonlinear robust codes based on the addition of two cubic networks. It allows to produce r-bit signatures to detect fault. This method offers good fault coverage. Yet, its hardware overhead is comparable to the hardware redundancy.

C = S ' + K (5)

where C={c i,j 0 ≤ i,j ≤ 3} is the round output.

The AES algorithm takes the cipher key and performs a Key Expansion routine to generate a key schedule. The key expansion generates a total Nb(Nr + 1) words, where Nb = 4.

Block diagram of the AES encryption is shown in Fig. 1.

The transformations in the decryption process perform the inverse of the corresponding transformations in the encryption process. In the AES decryption rounds, four transformations are used: InvShiftRows, InvSubBytes, AddRoundKey, and InvMixColumns. The AddRoundKey is the same for both encryption and decryption

In this paper, we consider the implementation of the 128-bit key system only, as this is the most commonly implemented form of AES.

• III.    Countermeasures Against Fault Attacks

In the literature, a large number of countermeasures proposed against fault attacks are based on some sort of redundancy: temporal redundancy, hardware redundancy and information redundancy.

• A.    Temporal Redundancy

In temporal redundancy, the same hardware is used to repeat the same process twice using the same input data. This technique uses minimum hardware overhead. Yet, it entails 100% time overhead.

• B.    Hardware Redundancy

In hardware redundancy, two copies of the hardware are used concurrently to perform the same computation on the same data. After each computation, the results are compared and every difference is reported as a fault. The advantage of this technique is that it can detect both transient and permanent faults. However, it requires at least 100% hardware overhead.

• IV.    The Proposed Fault Detection Scheme

In this section, we present the proposed fault detection scheme to protect the AES 128-bit implementations against fault attacks. It is noted that this scheme can also be applied to AES-192 and AES-256.

The proposed fault detection scheme structure for the AES is shown in Fig. 2.

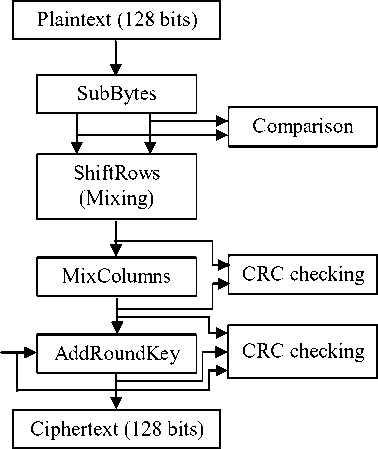
Figure 2. The proposed fault detection scheme structure for the AES

• A. In SubBytes

SubBytes, which is the only non-linear transformation in the AES, consists of 16 S-Box. Using the technique of parity to make the prediction parity for the SubBytes is complex due to nonlinearity of this transformation.

To protect the SubBytes, our method uses the hardware redundancy method. We implement two SubBytes transformations in parallel. At the end of SubBytes computation, the results are compared and every discrepancy is considered as a fault.

The same method can be applied in the decryption process by using two InvSubBytes transformation in parallel.

B. In ShiftRows

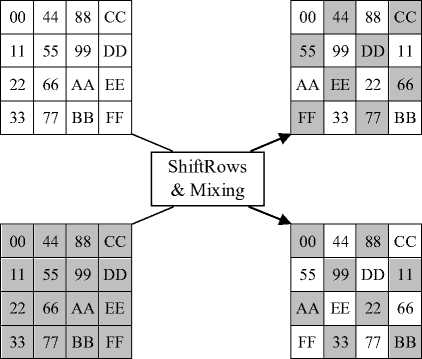
The output of the SubBytes transformation acts as the input to ShiftRows. As seen in (2), the output state of ShiftRows is obtained by shifting the matrix state. To secure the ShiftRows transformation, we used the scrambling method proposed in [19]. This method consists in scrambling the output of ShiftRows as presented in Fig. 3.

Data path A

Data path B

Figure 3. Scrambling bytes in ShiftRows [19]

f 5 ',0 =5  Ф 5 Ф 5 2^ Ф 5 30 = i=0

(02 Ф 03 Ф 01Ф 01)(5010 Ф 5lf0 Ф 52jо Ф 53j0)(6)

f 5 ',1 = 5 ' 01 Ф 5 11 Ф 5 11 Ф 5 11 = i = 0

(02 Ф 03Ф 01Ф 01)(50д Ф 51Д Ф 521 Ф 5зд)(7)

f 52 =5   Ф 5 '1,2 Ф 5 '2,2 Ф 5 '3,2 = i=0

(02 Ф 03 Ф01Ф 01)(5012 Ф 51;2 Ф 52j2 Ф 5312 )(8)

f 5 ',3 = 5 1з Ф 5 1з Ф 5 1з Ф 5 '3,3 = i = 0

(02Ф03Ф01Ф01)(50 з Ф5j 3 Ф52 з Ф 53 3)(9)

Considering the fact that 01 Ф 02 = 03, we have 02 Ф 03 Ф 01 Ф 01 = 01. Equations (6), (7), (8) and (9) can be rewritten as follows:

To improve the security of our AES implementation, the scrambling method can be applied at the bit level.

Data path A

Data path B

b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0

ShiftRows b7 b6 b5 b4 b3 b2 b1 b0

□ bit from data path A bit from data path B

b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0

b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0

Figure 4. Bit-level scrambling in ShiftRows

The bit level scrambling approach leads to a more robust implementation. Further, from a hardware viewpoint, it is easy to implement and does not increase the complexity.

The scrambling method can also be applied to the InvShiftRows transformation.

C. In MixColumns

The MixColumns is protected by using the cyclic redundancy check (CRC) [15]. According to (4), after adding the columns of S’, one reaches the following:

f 5 'i,0 =f1,(10)

i=0

f 5 'iA =f 5,1

i=0

f 5Ъ =f5i2(12)

i=0

f 5\3 =f5i3(13)

i=0

and

where f 5 '

f 5j j are the addition of the column

i = 0               i = 0

elements of the MixColumns state, and the ShiftRows state, respectively (0 ≤ j ≤ 3).

According to (10), (11), (12) and (13), the addition of the column elements of ShiftRows are equal to that of the corresponding column of MixColumns. At the end of the MixColumns computation, (10), (11), (12) and (13) are verified and every difference is reported as a fault.

The coefficients of InvMixColumns transformation are 09, 0B, 0D, 0E. The summation of the four coefficients used in decryption process, is also 1. Therefore, the CRC can be applied to the InvMixColumns transformation.

D. In AddRoundKey

The AddRoundKey operation adds the input state (output of the MixColumns) with round key K={k 0,0 ,k 1,0 ,….,k 3,3 } to obtain the output of the round.

We apply the cyclic redundancy check (CRC) to (5) to obtain:

3           3            3 2С» = 2s'Л0 ®2k^ i=0         i=0           i=0 (14) 33  3 2 cn=2 su ®2 кд i=0         i=0           i=0 (15) 33  3 2 ^3=2 s ®2 i=0         i=0           i=0 (16) 3           3            3 2ci3 =2s'i3 ®2ki3 i=0        i=0          i=0 (17) 3           3 where 2 С/ j , 2 s'/ j and i=0         i=0 3 2 kJ i=0 are the addition of the column elements of the round output, the MixColumns state and the round key, respectively (0 ≤ j ≤ 3).

At the end of AddRoundKey computation, (14), (15), (16) and (17) are verified and every discrepancy is considered as a fault.

• V.    Fault Detection

In this section, we describe the results of the simulation experiments which were carried out to evaluate the fault coverage of the proposed fault detection scheme for the encryption process. We injected random faults affecting any of the 128-bit state, with the number of faulty bits ranging from 1 to 20.

Figure 5. Simulation model

The simulation model is shown in Fig. 5. The fault detection scheme is simulated by 21 tests distinguished by the number of faulty bits in 128-bit AES state. The last test in table 1, labeled as random, used fault patterns with random faulty bit number. Each fault pattern has 2000000

blocks. Faults have been randomly injected, and the faulty operations and the faulty rounds were also randomly chosen. Simulation results are presented in table 1.

As seen in table 1, the percentage of the undetected faults dropped dramatically as the faulty bit number increased. For the random test, the percentage is about 0.001%. That means that the fault coverage achieves 99.999% for the proposed fault detection scheme.

Table 1. Detection Capabilities of the Proposed Fault Detection Scheme

Number of faulty bits	Percentage of the undetected faults
1	0%
2	1.1847%
3	0%
4	0.0851%
5	0%
6	0.0093%
7	0%
8	0.0013%
9	0%
10	0.0003%
11	0%
12	0.0002%
13	0%
14	0.00003%
15	0%
16	0.00003%
17	0%
18	0.00001%
19	0%
20	0.00001%
Random	0.001%

• VI.    FPGA Impelentation and Comparison

The original AES algorithm design and the proposed secured AES have been described using VHDL, simulated by ModelSim 6.6 and synthesized with Xilinx ISE 10.1.03. The FPGA target was XC5VFX70T from Xilinx Virtex-5 family.

As seen in table 2, the fault Coverage (FC), the number of occupied slices, the frequency (in megahertz), the throughput (in megabits per second), the area overhead and the frequency degradation for the original and secured AES implementation are presented.

Table 2. FPGA Implementation of the Proposed Fault Detection Scheme for the AES

AES Design	FC (%)	Area (slice) (Overhead)	Freq. (MHz) (Degradation)	Throu. (Mbps)
Original AES	-	342	263.92	2815.1 5
Protected	99.999	419	227.33	2424.8
AES		(22.51%)	(13.86%)	6

The implementation of our original AES takes 342 slices for 263.92 MHz Frequency. The protected AES occupies 22.51% more slices and the frequency decreases by 13.86% than the original AES.

We also compared our proposed method with some previous work for FPGA implementation and the results are shown in table 3.

Table 3. Fault Detection Schemes: Comparison

Fault Detection Schemes	FC (%)	Area Overhead (%)	Frequency Degradation (%)
Algorithm-level [21] *	100	97.6	23.48
Hardware Redundancy *	100	56.7	≈ 0
Structure-Independent [20]	99.996	26.9	≈ 0
Proposed Method	99.999	22.51	13.86

* The percentage are obtained from [20]

Compared to other works, our proposed method has the minimum area overhead and requires less frequency degradation than [21]. From a security viewpoint, the results show that the fault coverage achieves 99.999 % for the proposed scheme.

Therefore, these results show that our work achieves compromise between the implementation cost and the security of the AES.

• VII.    Conclusion

In this paper, in order to improve the security of the AES, we propose a fault detection scheme against the fault attacks. This method combines several countermeasures presented in the literature.

The proposed method has been implemented on Xilinx Virtex-5 FPGA. Its fault coverage, area overhead and frequency degradation have been obtained and compared.

Compared to some previous works, our proposed method has less area overhead and its fault coverage achieves 99.999%. Therefore the proposed fault detection scheme allows a trade-off between the security and the implementation cost of the AES.