A Robust Skin Colour Segmentation Using Bivariate Pearson Type IIαα (Bivariate Beta) Mixture Model

The skin colour segmentation has gained lot of importance due to its diversified applications in content based image retrievals, face detection, face tracking, gesture analysis, human computer interaction, computer vision etc., In all these areas it makes use of machine recognition of skin. The computer recognition is complex and difficult because of its limitations and static knowledge which are different from human endeavor. For efficient and effective design of skin colour segmentation algorithms it is needed to utilize statistical modeling [1].

The skin colour segmentation is a part of clustering and classification problem with respect to pattern recognition methodologies. Modeling the skin colour of humanbeings is very challenging task in image analysis since it is influenced by various factors such as illumination, camera characteristics, ethnicity, individual characteristics, subject appearance, background colour, shadow and motion etc., [2][3].

Another important difficulty in skin colour segmentation is that, the colour image senses work based on colour mosaic, which is assortment of different spectral filters [4]. Hence in skin colour segmentation the colour space plays a dominant role for feature extraction. In colour image it is customary to consider the RGB, Normalized RGB and CIE-xyz [5 - 9]. The perceptual colour space like TSL, HSL, HSV and HSI are developed for capturing the colour features more effectively [10 - 14]. To utilize the concept of orthogonal (independence of each other) colour spaces such as YCbCr, YIQ, YUV, and YES are developed [15 - 20]. The other colour spaces like CIE-Lab, CIE-Luv are also utilized extensively in colour image processing and analysis [21] [7] [22]. Among all these colour spaces the HSI colour space has certain advantages since it separate channels and outline certain colour properties which are close to the visual conjunctive system of human being [23] [24]. In HSI colour space the hue and saturation values are correlated through the intensity. That is the hue and saturation values of the pixel are the functions of pixel intensity. Hence recently in colour image processing the HS bivariate feature vector is utilized [25].

Recently much work has been reported in literature regarding skin colour segmentation. Cai and Goshtasb [26] have studied a method for detecting human faces in colour images using the skin separation. L.M. Bergassa et al. [8] have developed and analyzed an unsupervised and adaptive Gaussian skin colour model. Hayit Greenspan et al. [27] have considered the mixture of Gaussian distributions for modeling the space colour and segmentation. Kakhamanu et al. [28] have reviewed the methods for skin colour modeling and detection. Chang-Yul Kim et al [3] studied a practical system for detecting obscene videos. Ki-won Byun and Ki-Gon Nam [29] studied the skin region detection using mean shift algorithm based on the histogram approximation. Among all segmentation algorithms the model based segmentation methods are more efficient than other methods since they capture the local and global information of the images more effectively [30].

In model based skin colour segmentation it is customary to assume that the feature vector associated with the colour image is either Gaussian or Gaussian mixture model. But the Gaussian or Gaussian mixture model have certain drawbacks like the feature vector in each region are mesokurtic and having infinite range. In reality the feature vector in each region of the image (skin and non-skin regions) may not be mesokurtic and more so having finite range. To overcome this drawback in colour image segmentation based on Gaussian mixture model recently K.Srinivasarao et al [25] have developed the skin colour segmentation based on bivariate type 1Va mixture model. They assumed that the hue and saturation values of the skin and nonskin region follows Pearson type 1Va probability distributions with different parameters. The Pearson type 1Va is having the range from 0 to ∞ and also the bivariate distribution they consider is having a limitation of 0 < x < y where x and y are the values of hue and saturation.

But in general the hue and saturation values are having the range from 0 to 1 and they can not be constrained with the condition like x < y (x and y are hue and saturation values). To model the feature vector of the regions (skin and non-skin) it is reasonable to consider the bivariate Pearson type II aα model. Hence the whole image can be characterized by bivariate type II aα Pearson mixture model. The bivariate Pearson type II aα is having the marginal probability density for hue and saturation values as beta distributions which are having the range 0 to 1. They also include several types of frequency curves for different values of the parameters. This distribution also characterizes the negative correlation between the hue and saturation values of the image region. With this motivation, in this paper a skin colour segmentation algorithm is developed and analyzed by assuming the feature vector of the entire image following a bivariate Pearson type II aα mixture distribution.

The rest of the paper is organized as follows: section 2 given brief discussion about bivariate Pearson type II a α mixture model and its properties. Section 3 deals with the estimation of the model parameters using EM Algorithm. EM Algorithm is most efficient algorithm for estimating the model parameters in mixture distribution. Section 4 is to initialize the model parameters using moment method of estimation and K-means algorithm. In Section 5 the skin colour segmentation algorithm is presented based on likelihood function under Bayesian frame work. In section 6 the experimentation and performance evaluation of the proposed algorithm are discussed. The experimentation is carried with five face images take from JNTUK face database. The performance of the proposed algorithm is studied by computing the segmentation quality metrics like PRI, GCE and VOI. The efficiency of proposed algorithm is also studied through confusion matrix and ROC curves. Section 7 deals with conclusion and scope for further work in this area of research.

• II.    BIVARIATE PEARSON TYPE II a α MIXTURE MODEL

In skin colour analysis the classification of the image is done into two categories namely, skin and non-skin colour regions. The skin colour is different from the colour of most other natural objects in the world. To build the statistical model for the pixels in the image, the feature vector is extracted using colour spaces. In skin colour segmentation one has to use the chrominance component in extracting the features. Accordingly the hue and saturation under HSI colour space are used for skin colour detection. The statistical observations of hue and saturation which form a bivariate feature vector match closely with the bivariate Pearson type II a α distributions. The bivariate Pearson type II a α given by Kotz et al [31], is having non negative and asymmetric nature of the random variable. It also includes a wide variety of bivariate probability distributions. Here it is assumed that the feature vector of the pixel in skin or non-skin regions in the image follows a bivariate Pearson type II a α distribution. The Joint Probability density function of the feature vector is

f ( x , y / θ ) =

Γ(m + n + p) Γ(m)Γ(n)Γ(p)

x ^{m - 1} y ^{n - 1} (1 - x - y ) ^{p - 1}

m,n, p > 0

x, y > 0 and x+ y ≤ 1

0 is the parametric set such that 0 = ( m, n , p ) , x denote the hue value and y denote the saturation value of the pixel in the image.

The marginal probability density function of the hue value is f (x) = Beta (m, n + p )                      (2)

Its mean is

m m + n + p

Its variance is m (n + p )

( m + n + p + 1)( m + n + p ) ²

The marginal probability density distribution of the saturation value is f (y) = Beta (n, m + p)                      (3)

Its mean is

n m + n + p

Its variance is n (m + p)

( m + n + p + 1)( m + n + p ) ²

The Covariance between hue and saturation is

- mn

( m + n + p + 1)( m + n + p ) ²

The correlation coefficient between hue and saturation is mn

( n + p )( m + p )

Since the entire image is a collection of skin and nonskin pixel regions which are characterized by a bivariate Pearson type II a a distribution, the feature vector associated with the whole image is modeled as a two component bivariate Pearson type II a a mixture model. Its Joint probability density function is

h ^{( x} , У ) = Л - £ ^{( x} , У / ° )                    ⁽⁴⁾

i =1

Where, 0 <  a <  1 and a + a = 1 and f ( x , У ) is as given equation (1).

• III.    ESTIMATION OF THE MODEL PARAMETERS BY EXPECTATION MAXIMIZATION ALGORITHM

The likelihood function of sample bivariate observations ( x y ),( x y ),( x y ),...,( x y ) drawn from an image with probability density function K

h ( x , y ; 0 ) ^ ^ a Ji ( x s , y s ; 0 ) where f is the i =1

probability density function of a Pearson type II mixture distribution and is given by

L ( ° ) = П ( Л a , f, ( x s , y s ; 0 ) )

s=1

-^Г( m ⁺ n ⁺ ? ) m- Л n-HA v

= I I \ л a --------------- x y (1 — x —

1=1\=1 T( m )Г( n )Г( p)'

This implies that

NK log L(0) = log П (Л «f(xs, ys;°)) s=1

NK

=Л log(Z af (xs, ys ;0))(6)

s=1

The model parameters are estimated by using the Expectation Maximization Algorithm (E.M Algorithm). The updated equation of the parameter a _t is

1N akl   =ТтЛ[tk(xs,ys;°l))] for K = 1, 2.

N s =1

N

= ¹

N ^л

a l f к ( x_s y_s ; ° l ) ) k k s , s

Л a l f ^{( x}s , y s ; ° l) )

. i =1

^where , f_k ^{( x}s , ys^{; 0} l ) ) is as given equation (1).

The updated equation of m_k at ( l + 1) ^th iteration is

^N ( l )              ^N ( l )           1

^л tk ^{( x}s y$ ; ^{0   )lo}g^{( x}s ) ^+л tk ^{( x}s y$ ; ⁰ Укк,-------------- ;^{(—г (} mk + nk + pk )

s=1 k s, s              s    s=1 k s, s        Г(m + n + p )        k k k kkk

( — mk — nk — pk )

* log ⁽ log ⁽ e )) ^{+ Г ( m} _k ⁺ nk ⁺ p_k )* v ^{( m} _k ⁺ nk ⁺ p_k ))* log ^{( e} )

N              ( l )    ¹             .   .                            .      ^{— m}^

- ^л tk ( xs ys ; 0 У ----( -Г mk *log(log( e )) + Г mk * v ( mk ) * log( e )    ^k ) = 0

s=1      ,          Г mk where, ^(mk + nk + pk ) = digamma (mk + nk + pk )

The updated equation of n_k at ( l + 1) ^th iteration is

N

( l )                ^N ( l )

Z tk ⁽ xs , ys ; ^{9 llo}g⁽ ys ) ⁺ Z tk ⁽ xs , ys ; ^{9 7)}

=-----------;(-Г(mk + kk + pk) Г(m, + k, + p, )       k k k kkk

(— mk - kk - pk )

* log ⁽ log ⁽ e )) ^{+ r ( m} _k ^{+ k}k ⁺ Pk )* V ^{( m} _k ^{+ k}k ⁺ P_k ))* log ^{( e} )

mk

mk + kk + pk

= x k

^N               ( l )    ¹

- ^Z tk ( xsys ; S )---- (-Г k_k *log(log( e )) + Г kk * у ( kk )*log( e )

s =1      ,           ^Г kk

—I

n k ) = 0

nk

mk + kk + pk

where, v(mk + nk + pk ) = digamma(mk + nk + pk )

(mk + kk + pk + 1)(mk + kk + pk )2

s xyk

The updated equation of p_k at ( l + 1) th iteration is

N( s|1 tk (xs,ys;9   )log(1- xs- ys >+

N              (l)

Z tk (xs ys; 9   )------------------(-Г( mk + kk + pk) * log (log (e)) + s=1     ,         Г(mk + kk + pk)

Г ( mk + kk + pk )* V ( mk + kk + pk ))* log ( e )( ^k kpk )

N              (l)

^Z tk ( Xs ys ; 9 ( ) )-------( -Г ( pk ) * log(log( e )) + Г ( pk )* у ( pk )* log( e )

^s = 1      ^{,          Г}( pk )

^pk = 0

where, v(mk + nk + pk ) = digamma(mk + nk + pk )

where, x is the k ^th region sample mean of the Hue.

y is the k ^th region sample mean of the Saturation.

s               th xyk is the k  region sample between Hue and

Saturation

Solving the equations (11), (12), (13) we get the initial estimates of the parameters ( m ,n and p ) for K =  1, 2. Substituting these values as the initial estimates, we obtain the refined estimates of the parameters by using the EM-Algorithm.

Solving equations (7) (8) (9) and (10) iteratively using MATLAB code we get the revised estimates of a mk ⁿk Pk for K = 1, 2.

• IV.    INITILIZATION OF MODEL PARAMETERS BY K-MEANS

The efficiency of the EM-Algorithm in estimating the parameters is heavily dependent on the initial estimates of the parameters. The number of mixture components taken for K-means algorithm is two (skin and non-skin), i.e., K = 2. Usually the mixing parameter and the region parameters (m, n, and p) are unknown. A commonly used method in initialization is by drawing a random sample in the entire image data [32] [33]. This method perform well only when the sample size is large, and the computation time is heavily increased. When the sample size is small it is likely that some small regions may not be sampled. To overcome this problem, we use K-means algorithm [34] to divide the whole image into two homogeneous regions representing skin and nonskin regions. We obtain the initial estimates of the parameters m , n and p for each image region using the method of moment estimators for bivariate Pearson type II a a distribution and for the parameters 1

a as a = - for i = 1, 2.

i           i ₂

Therefore the initial estimates of m , n and p can be obtained by equating the theoretical moments with the sample moments. This implies

• V.    SKIN COLOUR SEGMENTATION ALGORITHM

After refining the parameters the prime step is skin colour segmentation, by allocating the pixels to the skin or non-skin segments. This operation is performed by segmentation algorithm. The skin colour segmentation algorithm consists of the following steps

• 1.    Divide the whole image into two regions using K-means algorithm

• 2.    Obtain the initial estimates of the model parameters using the moment estimators as discussed in section 4 for each region

• 3.    Obtain the refined estimates of the model parameters by using the EM-algorithm with the updated equations given in section 3.

• 4.    Substitute the estimated parameter values in the image joint probability density function

• 5.    Segment the pixels as skin colour or non-skin colour pixel using a threshold (t) and the likelihood

K

h(x, y)=Zaifi(x, y ;9) i=1

f (X, y / 9 ) .

where ⁱⁱ is as given equation (1).

• <      U л , L (X19) > t   L (x / 9) < t

function such that               or respectively for 0 < t < 1.

The optimal threshold value of t is determined computing true positive and false positive over the segmented regions and plotting the ROC Curve.

VI. EXPERIMENTAL RESULTS AND PERFORMANCE EVALUATION

classification rate of the skin pixels of the sample image using proposed model and Gaussian mixture model.

In this section, the performance of the developed skin colour segmentation algorithm is evaluated. For this purpose the skin images are collected from JNTUK database. A random sample of 5 images is taken from the database and the feature vector consisting of hue and saturation for each pixel of the each image is computed utilizing HSI colour space. In HSI colour space the hue and saturation values are computed from the values of RGB for each pixel in the image using the formula

Table.1 Miss Classification rate of the classifier

Model	Miss Classification Rate
bpt II a a mm	3.5%
GMM	8.3%

Hue=H=

cos

(R - G) + (R - B) 2^( R - G )2 + (R - B)(G - B)

1 - min( R, G, B)

Saturation = S =

I

From the Table.1 it is observed that the misclassification rate of the classifier with bivariate Pearson type II a a mixture model (BPTII a a MM) is less compared to that of GMM.

The accuracy of the classifier is also studied for the sample images by using confusion matrix for skin and non-skin regions. Table.2 shows the values of TPR, FPR, Precision, Recall and F-measure for skin and nonskin segments of the sample images.

where I =

R + G + B

is the intensity of pixel.

With the feature vector (H, S) each image is modeled by using the two component bivariate Pearson type II a a mixture distribution. The initial values of the model parameters are obtained by dividing all the pixels into two categories namely skin and non-skin region using K-means algorithm with K = 2 and taking the moment estimates for ( m , n and p ), K = 1, 2. Using these initial estimates and the updated equations of the EM-Algorithm discussed in section.3 with MATLAB code the refined estimates of model parameters are obtained. Substituting the refined estimates in the bivariate Pearson type II a a joint probability distribution function the skin colour and non-skin colour models of each image are estimated. The segmentation algorithm with component maximum likelihood under Bayesian frame and a threshold value t as discussed in section 5 is used to segment the image. Figure.1 shows the original and segmented images.

Table.2 Comparative study of GMM and BPTII a ^a MM

Image	Method	TPR	FPR	Precision	Recall	F-measure
Image 1	BPTII a a MM	0,9642	0.0625	0.9818	0.9642	0.9640
(Malel)	GMM	0.9285	0.1875	0.9454	0.9285	0.9368
Image2	BPTII a a MM	0.9625	0.0181	0.9788	0.9625	0.9705
(female!)	GMM	0.9166	0.0833	0.9565	0.9166	0.9363
Image3	BPTII a a MM	0.9692	0.0600	0.9767	0.9692	0.9729
(Male2)	GMM	0.9307	0.0700	0.9718	0.9307	0.9508
Image4	BPTII a a MM	0.9629	0.0363	0.9848	0.9629	0.9737
(female2)	GMM	0.9259	0.0454	0.9803	0.9259	0.9260
Image 5	BPTII a a MM	0.9800	0.0187	0.9849	0.9800	0.9824
(Male3)	GMM	0.8750	0.0625	0.9459	0.8750	0.9090

From Table.2 it is obtained that the F-measure value for the proposed classifier is more. This indicates the proposed classifier perform better than that of Gaussian mixture model. Figure.2 shows the ROC curves associated with the proposed skin colour classifier and the classifier with GMM.

Figure.1 Original and Segmented Images

The developed algorithm performance is evaluated by comparing skin colour segmentation algorithm with the Gaussian mixture model. Table.1 present the miss

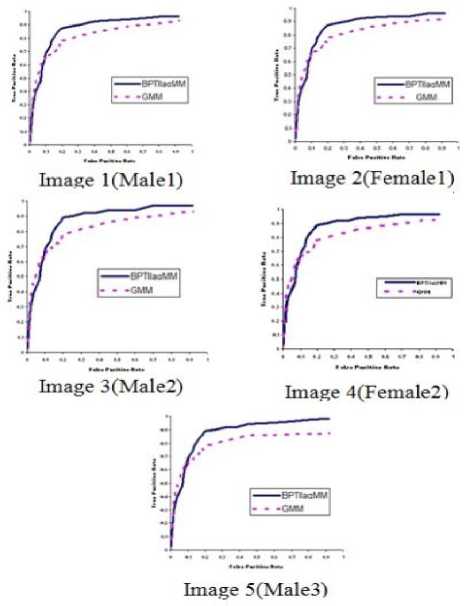
Figure. 2 ROC Curves

From Figure.2 it is observed that the proposed classifier is having less false detection of the skin pixels compared to the classifier with GMM. The figure also shows that, it can successfully identify the exposed skin region including face, hands and neck.

The performance of the segmentation algorithm is also studied by obtaining three segmentation performance measures namely, Probabilistic Rand Index (PRI) [35], Variation of Information (VOI) [36], Global Consistency Error (GCE) [37], with the sample images. The computed values of the performance measures for the developed algorithm with BPTII a α MM and GMM are presented in Table.3.

Table.3 Segmentation Performance Measures

Image	Method	Performance Measures
		PRI	GCE	VOI
Image 1	BPTIIatzMM	0,6941	0.1928	0.0924
(Malel)	GMM	0.5128	0.2486	0.1529
Image 2	вртпдамм	0,7810	0.2016	0.0816
(Femalel)	GMM	0.5367	0.2249	0.0981
Image 3	BPniaaMM	0,6721	0.1281	0.0926
(Male2)	GMM	0,4826	0.1924	0.1626
Image 4	врпиамм	0,7941	0.0972	0.0831
(FcmaleZ)	GMM	0.6124	0,1362	0.1472
Image 5	ВРТПяаММ	0.7214	0,1902	0.0662
1Ма1ф)	GMM	0.5924	0.2136	0.12/1

From the Table.3 it is observed that the PRI value of the proposed algorithm for sample images considered for experimentation are more than that of the value from the segmented algorithm based on GMM and they are closed to 1. Similarly the GCE and VOI values of the proposed algorithm are less than that of finite Gaussian mixture model and close to 0. This reveals that the proposed segmentation algorithm performs better than the algorithm with GMM and the proposed skin colour segmentation is close to the ground truth.

• VII. Conclusion

In this paper we proposed a skin colour segmentation algorithm based on bivariate Pearson type mixture model using HSI colour space. Here it is assumed that the bivariate feature vector (Hue and Saturation) of the whole image follows a bivariate Pearson type II a α mixture distribution which is capable of characterizing the skin and non-skin colours in the image. The bivariate Pearson type II a α distribution is having marginal distributions as beta distributions with range 0 and 1, having the negative correlation coefficient and their features closely match the hue and saturation statistical characteristics of the skin and non-skin regions. This model also includes various types of bivariate distribution for specific values of the parameters. As this distribution is having three parameters only, it is a parsimonious model. The model parameters are obtained by deriving the updated equations of the EM-Algorithm. The initialization of the parameters is done using K-means algorithm and moment method of estimation. The experimental results with different types of five face images taken from JNTUK database revealed that the proposed algorithm perform much superior with respect to image segmentation performance metrics like PRI, GCE and VOI. A comparative study of proposed model with that of the GMM has shown that the proposed algorithm outperforms the existing algorithm for some images in skin colour segmentation. This is also supported by ROC curves. This algorithm can also be further extended to unsupervised skin colour segmentation with more number of regions of the image such as background, skin colour, non human objects etc. It is also possible to develop a skin colour segmentation based on bivariate Pearson type mixture model and hidden markov model which will be taken else where.